基于位置和速度信息的GNSS卫星坐标多项式插值法*

宋传峰 党亚民 秘金钟 薛树强

(中国测绘科学研究院，北京 100830)

基于位置和速度信息的GNSS卫星坐标多项式插值法*

宋传峰 党亚民 秘金钟 薛树强

(中国测绘科学研究院，北京 100830)

用户在对精密星历或广播星历进行多项式拟合与插值时，会受到龙格现象的影响。利用卫星的位置和速度信息，可有效地减弱龙格现象的影响，8 h多项式插值弧段在检核点处的残差均在mm级。

全球导航卫星系统;精密星历;广播星历;多项式插值;龙格现象

GNSS卫星在导航定位中是动态已知点，精确确定GNSS卫星的坐标是卫星导航定位的基础。卫星的位置可以由广播星历或精密星历计算得到。精密星历由间隔15 min的离散数据点组成，要获得任意时刻的卫星坐标，需要采用拟合或插值的方法。拟合或插值卫星轨道的方法有拉格朗日插值、切比雪夫多项式等。在进行多项式拟合或插值GNSS精密星历时，为了达到需要的精度，常选择较高阶数的多项式，但随着阶数的增加，在拟合与插值节点处龙格现象尤为明显［1－3］。传统的做法是通过拼接相邻天的星历数据采用滑动窗口的方法进行计算，或多项式拟合时只取中间有效弧段，这样不仅给用户带来了不便，而且数据利用率不高。

由于插值弧段在两端缺少控制，在多项式插值时会产生龙格现象，而插值节点处的趋势项信息能控制多项式的走向，有效地抑制龙格现象。本文利用卫星的位置和速度信息进行多项式拟合与插值，有效地减弱了龙格现象的影响，8 h插值弧段在检核点处的残差均在mm级，与IGS精密星历精度相比完全可以忽略。

1 基于位置和速度信息的多项式插值法

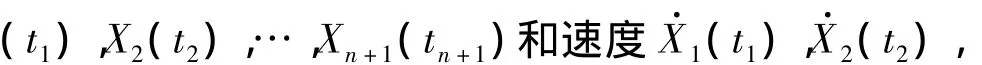
由于速度与位置相比是无穷小量，若直接用式(1)求解参数显然不合理。为了使速度信息在求取多项式系数时与位置信息起到相同的作用，需要合理确定观测方程的权阵。

实际中，卫星的位置和速度都是通过特定的函数模型计算得到的，如精密星历中的卫星位置和速度是在轨道积分过程中求解的，广播星历中卫星位置和速度是按星历发布时刻的轨道参数计算得到的。避开不同函数模型之间的差异，则获得任意时刻卫星位置和速度观测值的函数模型为:

仅考虑高次项，则式(4)可近似表示为:

忽略不同时刻卫星位置间的相关性及同一时刻卫星位置和速度间的相关性，仅考虑同一时刻卫星位置和速度的观测精度不同，则观测方程权阵为:

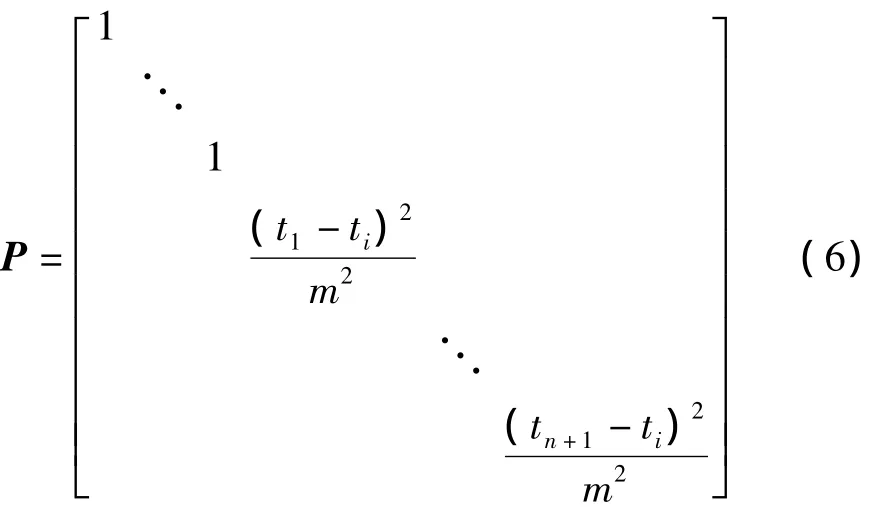
弧段内任意时刻卫星坐标为:

2 算例分析与比较

2.1 精密星历的多项式插值

SP3格式的精密星历给出了15 min等间隔的卫星位置信息［4］，由于不直接包含速度信息，为了验证速度信息在多项式插值时的作用，先通过滑动窗口的拉氏插值法计算出各节点的速度，然后再基于位置和速度信息将一较长弧段表示成多项式。

使用IGS发布的1 686周第3天的最终精密星历，利用16阶多项式对G01号卫星坐标进行多项式插值(m=n)，插值区间为2012-05-02 00:00～08:00(GPST)。为便于精度分析，每隔30 min选取一控制点进行多项式系数计算，所有时间间隔15 min的节点均作为检核点。图1为利用位置和速度信息与仅利用位置信息进行精密星历多项式插值在检核点处的卫星三维坐标残差。

2.2 广播星历的多项式插值

广播星历精度稍差，但可直接获得位置和速度信息。由文献［5］可知，不同时刻发布的广播星历之间符合性不是很好，拟合成多项式时会产生跳跃。首先由插值弧段中间时刻附近发布的广播星历计算出间隔15 min的卫星位置和速度，然后基于式(1)、(6)利用广播星历中的位置和速度信息，将广播星历拟合成一m阶多项式。

图2为利用位置和速度信息与仅利用位置信息进行广播星历多项式插值在检核点处的卫星三维坐标残差。

2.3 结果分析

1)由图1、2可知，仅利用位置信息进行多项式插值时在插值弧段两端产生了严重的震荡现象，其最大误差可达dm级;而基于位置和速度信息的多项式插值，卫星坐标几乎不受龙格现象的影响，其在检核点处的残差均在2 mm内，这与星历本身精度相比完全可以忽略。

图1 精密星历多项式插值卫星三维坐标残差Fig.1 Satellite coordinates residuals of polynomial interpolation of precise ephemeris

图2 广播星历多项式插值卫星三维坐标残差Fig.2 Satellite coordinates residuals of polynomial interpolation of broadcast ephemeris

2)算例中，为了进行精度分析，选取采样间隔为30 min的控制点进行多项式系数计算，但实际中若采用间隔为15 min或更小的控制点则将会获得更高的插值精度。

3)算例分析表明，利用趋势项信息可明显减弱龙格现象，若使用更长的插值弧段则需要提供更高阶的趋势项信息来减弱龙格现象的影响。

3 结语

通过精密星历多项式插值和广播星历多项式插值，验证了利用趋势项信息能有效减弱龙格现象，但不同类型信息之间需要合理地配权。在实际应用中，可考虑利用趋势项信息来进行多项式拟合或插值，其他插值方法也可以利用趋势项信息来减弱龙格现象的影响。

1 洪樱，欧吉坤，彭碧波.GPS卫星精密星历和钟差三种内插方法的比较［J］.武汉大学学报:信息科学版，2006(6):516 －518.(Hong Ying，Ou Jikun，Peng Bibo.Three interpolation methods of precise ephemeris and clock offset of GPS satellite［J］.Geomatics and Information Science of Wuhan University，2006(6):516 －518)

2 Feng Y，Zheng Y.Efficient interpolations to GPS orbits for precise wide area applications［J］.GPS Solution，2009(9):67－72.

3 邱蕾，廖远琴，花向红.基于IGS精密星历的卫星坐标插值［J］.测绘工程，2008(4):15 －18.(Qiu Lei，Liao Yuanqin，Hua Xianghong.Interpolation methods for satellite coordinate based on IGS precise ephemeris［J］.Engineering of Surveying and Mapping，2008(4):15 －18)

4 刘刚，邵楠.两种IGS精密星历多项式插值方法的比较分析［J］.城市勘测，2012(10):107 －109.(Liu Gang，Shao Nan.Comparison and analysis of two methods for IGS precise ephemeris interpolation［J］.Urban Geotechnical Investigation and Surveying，2012(10):107 －109)

5 Horemuz M，Andersson J.Polynomial interpolation of GPS satellite coordinates［J］.GPS Solution，2006(10):67 －72.

POLYNOMIAL INTERPOLATION OF GNSS SATELLITE COORDINATES BASED ON POSITION AND VELOCITY INFORMATION

Song Chuanfeng，Dang Yamin，Bi Jinzhong and Xue Shuqiang
(Chinese Academy of Surveying and Mapping，Beijing 100830)

Polynomial fitting and interpolating of precise or broadcast ephemeris will be affected by Runge’s phenomenon.Satelites’position and velocity information were used to remove the influence of Runge’s phenomenon.The result shows that the outside precision of 8-hour fit interval can reach millimeter level.

GNSS;precise ephemeris;broadcast ephemeris;polynomial interpolation;Runge’s phenomenon

P228

A

1671-5942(2014)03-0108-03

2013-09-10

科技部863计划重点项目(2011AA120503);科技部科技支撑计划项目(2012BAB16B01);科技部863计划项目(2013AA122501);北斗分析中心项目(GFZX0301040308-06)。

宋传峰，男，1987年生，硕士研究生，主要从事GNSS卫星定轨与测量数据处理的研究工作。E－mail:297933297@qq.com。