基于恒星日滤波的PPP多径误差消除研究*

郑 彬 周 宁 欧 钢

1)国防科技大学电子科学与工程学院，长沙 410073

2)江南计算技术研究所，无锡 214083

基于恒星日滤波的PPP多径误差消除研究*

郑 彬1，2)周 宁2)欧 钢1)

1)国防科技大学电子科学与工程学院，长沙 410073

2)江南计算技术研究所，无锡 214083

基于PPP的数学模型，分析多径误差对PPP定位结果的影响。研究表明，对PPP应用恒星日滤波时解算区间、数据采样率等定位参数应保持一致。通过对定位偏差序列的拉格朗日插值，可以将恒星日滤波应用到低采样率的观测数据中，拓宽恒星日滤波的应用范围，降低处理计算量。针对IGS跟踪站的数据，应用恒星日滤波多径误差修正后，PPP动态定位的精度有了明显改善，东、北、天3方向的精度分别提高了69.2%、72.3%、27.6%。关键词 精密单点定位;多径误差消除;恒星日滤波;拉格朗日插值;IGS

精密单点定位(PPP)利用精密星历、钟差以及载波相位观测值，使用单站GPS观测数据可以达到cm级乃至亚cm级的定位精度，在地壳运动、形变监测等领域得到越来越广泛的应用［1－2］。PPP中，星历、星钟、电离层延迟、对流层延迟、天线相位中心等误差可以通过参考站网络或模型精确修正。然而由于接收机天线所处的几何环境的特殊性和复杂性，多径误差不能通过建立一个简单的数学模型来修正［3］。因此，对于精密定位来说，多径误差是影响定位精度的主要误差源［4］。

对于静止的接收机来说，由于GPS卫星运动周期的重复性，卫星和接收机周围任何固定反射物的几何关系在约一个恒星日周期后重复［5－6］，利用这一特性，可以通过连续多天的同时段观测消除多径误差，即恒星日滤波。恒星日滤波最早应用于差分定位［6－7］中，Choi、Ragheb 等分别通过卫星轨道重复周期和定位结果的相关性确定恒星日滤波周期，利用恒星日滤波对短基线双差定位结果进行了改进。随着PPP研究的深入，近年来恒星日滤波方法也逐渐应用到PPP地表形变分析中［2］。然而，现有PPP恒星日滤波相关文献的研究集中在应用层面，尚缺乏系统的理论分析。

本文首先结合PPP的数学模型分析多径误差对定位结果的影响，指出对PPP应用恒星日滤波应遵循的规则，而后给出了PPP恒星日滤波的处理流程，最后通过对IGS监测站的实测数据的分析，验证了文中的结论。

1 PPP数据处理

1.1 数学模型

PPP利用双频电离层无关组合来消除一阶电离层延迟项，其观测方程如下:

式中，ℓP、ℓΦ分别为码和载波相位的电离层无关组合，ρ为卫星-接收机几何距离，C为光速，dt为接收机钟差，dT为卫星钟差，Tr为对流层延迟，N为载波相位模糊度(包含初始相位)，λ为电离层无关组合的载波波长，εP、εL为码和载波相位的测量噪声(含多径误差)。

式(1)中，将对流层延迟用天顶延迟zpd和映射函数M代替，消除已知的卫星钟差，得:

将式(2)在先验位置和观测值(X0，ℓ)附近线性化，可得［8］:

其中，A为设计矩阵，即观测方程对未知参数X的偏导数，δ为修正矢量，W=f(X0，ℓ)为闭合差矢量，V为残差。

加权最小二乘解为:

其中PX0、Pℓ分别为先验值和观察量的协方差矩阵。则X的估计值为:

1.2 误差传递分析

对单历元定位，观测量中的多径误差叠加在闭合差矢量W中，影响了最小二乘求解的结果，造成估计值与真值的偏差。由式(4)、(5)可知，设计矩阵A仅与卫星坐标和星地距离有关，对于静止的接收机相隔一个恒星日的两个观测时刻，卫星坐标与星地距离均相同，因而设计矩阵A相同。而又由于卫星几何布局的一致，由测站附近固定反射体引起的观测值中的多径误差也相同。结合式(7)，相隔恒星日周期的单历元定位的坐标误差也一致，因而可以利用前一恒星日的坐标误差修正后一恒星日的定位结果，从而提高定位精度。

另一方面，PPP定位与差分定位(短基线)不同。差分定位中，模糊度参数为整数，且电离层误差直接通过差分消除，可以逐历元解算模糊度，各历元估计结果完全独立［7］。PPP定位中，由于模糊度参数需要较长时间滤波才能收敛，各历元间估计结果不独立，定位结果不仅与当前时刻有关，也与之前的观测有关。如果要对PPP应用恒星日滤波，前后两天解算区间的长度、数据采样率等须保持一致。

2 恒星日滤波

2.1 滤波周期的确定

理论上GPS卫星轨道周期为半个恒星日(11 h 58 min 2 s)，地球自转周期为一个恒星日(23 h 56 min 4 s)，经过1个恒星日后地面与卫星的几何关系重复。然而，由于GPS卫星在飞行过程中受到地球和月球引力场的影响，以及地面控制站的调控，其实际重复周期并非正好为一个恒星日。根据广播星历的轨道参数可以计算重复周期［5］:

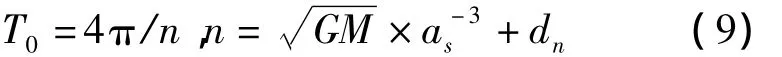
其中，GM(=3.986 005×1014m3/s2)为地球引力常数，as为卫星椭圆轨道长半轴的平方根，dn为平均运动角速度的改正量。文献［5］计算了2006年前100 d的平均周期，得出重复周期相对于平太阳日(86 400 s)提前约246 s。文献［9］指出，一天内有小部分时段地面站观测到的轨道重复周期相对于86 400－246 s有波动，差值可达10 s，在针对波动时段计算轨道周期修正后，定位结果可改善5%左右。为简化分析，本文采用246 s作为平移时间。

2.2 滤波方法

恒星日滤波法的具体流程如下:

1)对测站连续多天的GPS观测数据进行PPP动态定位，将定位偏差序列通过移动平均法进行低通滤波，消除高频噪声的影响。

2)对前几天的低通滤波偏差依据改进的恒星日周期进行对应时刻的平均，构建多径误差改正模型。

3)将多径误差改正模型应用到下一天，可以获得经过多径误差改正后的PPP动态定位结果。

PPP定位中，定位误差包含了星历误差、星钟误差、测量噪声、建模误差、多径误差等。对于IGS精密星历和卫星钟差，其误差在1～2 cm［8］，且可视为正态分布，载波相位测量噪声为高斯白噪声，误差为mm级，建模误差(包括高阶电离层延迟、对流层模型等的影响)也为mm级。对于Kalman滤波，高斯白噪声对估计结果的影响可以通过滤波消除，噪声保留在滤波残差中。而由于多径误差的有色噪声特性以及恒星日重复性，可以认为多天定位结果中的相似误差主要为观测量中多径误差的影响，从而可以通过多天的定位误差序列提取多径误差改正模型。

由于平移时间为246 s，如果是1 Hz高采样率的GPS观测量，可以直接平移。但高采样率的观测也带来以下两方面的问题:①数据量大，处理时间长，例如采样率为1 Hz的24 h的RINEX观测数据可达100 MB左右［9］;②高采样率的观测数据也要求提供对应的高采样率卫星钟差，以避免钟差插值误差对定位结果的影响。而当前IGS提供的事后精密钟差最高为30 s间隔，CODE最高可以提供5 s采样间隔的精密钟差产品。鉴于此，对于采样频度低于1 Hz的观测数据(如IGS提供的单天观测数据的采样间隔为30 s)，可以通过对定位偏差在指定时刻进行Lagrange插值得到改正序列。插值方法如下:

其中，n为插值阶数，x为观测时刻序列，y为偏差序列。通过对定位偏差序列的Lagrange插值，可以将恒星日滤波应用到低采样率的观测数据中，拓宽恒星日滤波的应用范围。

3 实例分析

本文基于开源的 RTKLIB软件［10］来进行 PPP动态定位，各种误差的修正及处理策略见表1。精密星历、卫星钟差、卫星和接收机天线相位中心改正模型、基准坐标等从IGS数据产品中获取，卫星观测截止角选为10°，电离层误差通过双频电离层无关组合消除，天顶对流层延迟采用随机游走模型估计。由于PPP的模糊度参数收敛需要0.5～1 h，模糊度收敛之前定位精度偏低，采用正反向 Kalman滤波［11］事后处理，将正向的滤波结果作为初始信息再进行反向滤波，反向滤波的结果作为最终结果。这样，可以在整个观测时段内都获得高精度的定位结果。

表1 PPP数据处理策略Tab.1 Processing of PPP data

利用上述方法对IGS监测站ZIM2进行分析，采用静态观测数据模拟动态PPP定位，定位结果与IGS周解中的基准坐标之差为定位误差。首先比较不同解算参数对PPP定位结果的影响。选取观测时段为2011年第096～099 d，其中第099 d处理区间为00:00:00开始，第098～096 d依次偏移240 s。选取3种不同的观测区间长度、采样间隔组合进行比较分析，分别为长度4 h间隔30 s(图1(a))、长度8 h间隔60 s(图1(b))、长度8 h间隔30 s(图1(c))。

图1给出了不同处理参数下的定位误差序列，其中深色表示099 d误差序列，浅色表示对096～098 d的误差序列进行滤波平均后的结果，E-W、NS、U-D分别表示东、北、天方向。

1)经过低通滤波和多天平均后，消除了高频和随机噪声的影响，定位误差序列较平滑;

2)对不同天的数据采取相同解算参数得到的定位结果具有较强的相似性;

3)选取不同的观测区间、采样率对PPP处理结果有影响。

图1 解算参数对定位偏差的影响Fig.1 Influence of solution parameters on position error

为进一步对不同解算参数的影响进行量化分析，采用Pearson相关系数对误差序列进行相关性分析，其定义为:

其中，σQC为协方差，σQ、σC为标准差，¯q、¯c为序列的均值。相关系数的取值范围为［－1，1］，正数表示正相关，负数表示负相关，Pearson相关系数绝对值越大表明相关度越高。

表2给出了这6组定位结果进行相关性分析的结果。可见，相同的滤波区间长度和采样率条件下，不同天的东向(E)、北向(N)定位误差具有最大的相关性(表2中对角线所示元素)。如果滤波区间长度或采样率不一致，误差的相关性会减弱，两者均不一致的情况下相关性最弱。PPP解算参数对天顶(U)方向误差的影响不明显，采用不同参数得到的定位误差序列的相关系数很接近，且最优情况下的相关性不如东向和北向。这可能是由于天顶方向本身定位误差比较大、噪声比较高而引起的(图1中天顶方向误差波动较大)。综上所述，对PPP进行恒星日滤波，应保持观测区间、采样率一致，才能通过不同天多径效应引起的定位误差的相关性，来最大限度地消除多径误差的影响。

对ZIM2站096～099 d进行了恒星日滤波实验，以096～098 d共3 d的定位结果建立多径误差改正模型，对099 d的定位结果进行改正。观测长度为4 h，采样间隔为30 s。由图2可见，经过恒星日滤波后，PPP动态定位的精度有了明显改善。与IGS周解的标准位置相比，初始的东北天坐标3分量的精度(RMS)分别为 3.51、1.95、3.48 cm，恒星日滤波改正后的精度分别为1.06、0.54、2.52 cm，3方向分别提高了69.2%、72.3%、27.6%。

4 结语

结合PPP的数学模型，分析了多径误差对PPP定位结果的影响以及应用恒星日滤波消除PPP多径误差的原理。由于PPP的数据处理机制，模糊度参数需要较长时间滤波才能收敛，各历元间估计结果不独立，定位结果不仅与当前时刻有关，也与之前的观测有关，因而对PPP进行恒星日滤波时解算区间、数据采样率等定位参数应保持一致。对IGS测站的实际数据进行分析表明，采用恒星日滤波消除多径误差，可以有效改善PPP动态定位的精度。

图2 恒星日滤波前后定位误差比较Fig.2 Comparison of position error before and after sidereal filtering

需要指出的是，应用PPP恒星日滤波需要已知滤波前几日观测站的精确坐标，其中精确坐标采用观测站地震前/结构振动前的静态定位坐标，从而消除形变/振动序列中的多径误差，得到更精确的定位结果。

1 Kouba J.A possible detection of the 26 December 2004 great Sumatra－Andaman islands earthquake with solutions products of the international GNSS service［J］.Stud Geophys Geod，2005，49(4):463 －483.

2 方荣新，施闯，辜声峰.基于PPP动态定位技术的同震地表形变分析［J］.武汉大学学报:信息科学版，2009，34(11):1 340 － 1 343.(Fang Rongxin，Shi Chuang，Gu Shengfeng.Precise point positioning with high－rate GPS data applied to seismic displacements analysis［J］.Geomatics and Information Science of Wuhan University，2009，34(11):1 340－1 343)

3 Yang Yunchun，Hatch R R，Sharpe R T.GPS multipath mitigation in measurement domain and its applications for high accuracy navigation［C］.17th International Technical Meeting of the Satellite Division of The Institute of Navigation(ION GNSS 2004)，Long Beach，CA，2004.

4 Phan Q H，Tan S L，Ian McLoughlin.GPS multipath mitigation:a nonlinear regression approach［J］.GPS Solut，2013，17:371－380.

5 Wu J，Hsieh C H.Statistical modeling for the mitigation of GPS multipath delays from day－to－day range measurements［J］.J Geod，2010，84:223 － 232.

6 Choi K，Bilich A，Larson K M，et al.Modi fi ed sidereal fi ltering:implications for high－rate GPS positioning［J］.Geophys Res Lett，2004，31:L22608.

7 Ragheb A E，Clarke P J，Edwards S J.GPS sidereal fi ltering:coordinate－and carrier－phase－level strategies［J］.J Geod，2007，81(5):325 －335.

8 Kouba J，Heroux P.Precise point positioning using IGS orbit and clock products［J］.GPS Solutions，2001，5(2):12 － 28.

9 殷海涛，甘卫军，肖根如.恒星日滤波的修正以及对高频GPS定位的影响研究［J］.武汉大学学报:信息科学版，2011，36(5):609 － 611.(Yin Haitao，Gan Weijun，Xiao Genru.Modified sidereal filter and its effect on high－rate GPS positioning［J］.Geomatics and Information Science of Wuhan University，2011，36(5):609 －611)

10 Takasu T.RTKLIB:Open source program package for RTKGPS［C］.FOSS4G 2009，Tokyo，2009.

11 阮仁桂，郝金明，刘勇.正反向Kalman滤波用于动态精密单点定位参数估计［J］.武汉大学学报:信息科学版，2010，35(3):279 － 282.(Ruan Rengui，Hao Jinming，Liu Yong.Using a forward－backword Kalman filter to estimation parameters for kinematic precise point positioning［J］.Geomatics and Information Science of Wuhan University，2010，35(3):279－282)

致谢 感谢T Takasu提供开源PPP处理软件RTKLIB，IGS提供观测数据及精密星历、钟差产品。

STUDY ON ELIMINATION OF MULTIPATH ERROR IN PPP BASED ON SIDEREAL FILTERING

Zheng Bin1，2)，Zhou Ning2)and Ou Gang1)
1)College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073)
2)Jiangnan Institute of Computing Technology，Wuxi214083

Based on PPP mathematic model，the impact of multipath error on PPP solution is investigated.The result of analysis indicates that all positioning parameters，such as solution constant interval and sampling rate，have to be consistent with each other on different observation days in opperating PPP sidereal filtering.Sidereal filtering can be applied to low sampling rate observations by Lagrange interpolation of position error time series，which spreads its application and decreases calculation amount.Experimental result analyzing the data from IGS tracking stations shows that accuracy of PPP kinematic position accuracy can be improved with the sidereal filtering by 69.2% ，72.3%and 27.6%for the East，North and Up components.

precise point positioning;multipath mitigation;sidereal filtering;Lagrange interpolation;IGS

P228.41

A

1671－5942(2014)03－0178－05

2013－11－18

新世纪优秀人才支持计划项目(NCET－04－0995)。

郑彬，男，1985年生，博士生，主要研究方向为精密单点定位。E－mail:bingo.zheng@gmail.com。