海底地形反演方法比较*

胡敏章 李建成 邢乐林 翟振和 欧阳明达

1)中国地震局地震研究所(地震大地测量重点实验室)，武汉 430071

2)中国地震局地壳应力研究所武汉科技创新基地，武汉 430071

3)武汉大学测绘学院，武汉 430079

4)武汉大学地球空间环境与大地测量教育部重点实验室，武汉 430079

5)西安测绘研究所，西安 710054

海底地形反演方法比较*

胡敏章1，2，3，4)李建成3)邢乐林1，2)翟振和5)欧阳明达5)

1)中国地震局地震研究所(地震大地测量重点实验室)，武汉 430071

2)中国地震局地壳应力研究所武汉科技创新基地，武汉 430071

3)武汉大学测绘学院，武汉 430079

4)武汉大学地球空间环境与大地测量教育部重点实验室，武汉 430079

5)西安测绘研究所，西安 710054

研究比较了海底地形反演的空域法、频域法和最小二乘配置法，选择3个2°×2°实验区域进行海底地形实算。结果表明，空域法计算结果精度虽然较频域法和最小二乘配置法略高，但计算速度非常慢，不适用于大区域海底地形模型的计算;频域法由于可以采用FFT算法，计算速度很快，精度也较高;最小二乘配置法需要已知海底地形的详细统计信息，这与海底地形反演目的相矛盾。本文还采用频域法，联合垂直重力梯度异常和船测海深数据反演了实验区域海底地形，验证了垂直重力梯度异常数据用于海底地形计算的可行性。

海底地形;重力异常;空域法;频域法;最小二乘配置法

海底地形反演是卫星测高的一大应用领域，自Dixon等［1］首次采用Seasat沿轨大地水准面数据计算海底地形以来，众多学者都研究了由测高重力异常/大地水准面反演海底地形的理论和方法，反演计算了大量局部或全球海底地形模型［2－15］。Calmant［11］对卫星测高数据反演海底地形的理论和方法进行了详细总结。Wang［16］提出根据重力垂直梯度异常数据反演海底地形的方法，并认为该方法计算得到的海底地形模型与重力异常相互独立，能够用于海底均衡状况的三维导纳分析。吴云孙等［8］对此进行试验，但由于梯度数据短波部分噪声很大，效果并不理想。胡敏章等［10］采用模拟数据，研究了根据垂直重力梯度异常反演海底地形的方法。

本文总结归纳现有海底地形反演方法，并通过实际数值计算，对比分析各方法的优劣。分别根据重力异常和垂直重力梯度异常，采用频域法反演了实验区海底地形，比较了两种数据反演结果，说明垂直梯度异常数据也可用于海底地形反演。

1 海底地形反演方法

1.1 空域法

如图1所示，Q表示相对于参考海深的一个高为h的海底地形，a为地球平均半径，Rref=a+d，d为参考海深，ψ为P与流动点Q之间的球心角。海面上点P受Q处海底地形异常物质产生的重力异常影响的计算公式为:

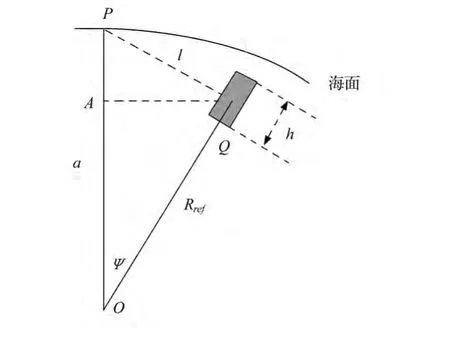
图1 海底起伏的重力效应Fig.1 Gravity effect of the seafloor undulation

式中，ΔgP表示P点周围n个格网点的地形起伏在P 点产生的重力异常，ΔΩi、hi、ψi分别表示第 i个格网点的面元积分、地形起伏及其与P点的球心角距，面元积分近似为:

式中，θ为积分流动点余纬，Δλ、Δφ分别为格网的经度方向和纬度方向大小，φQ为格网中心纬度。

式中，B=R － acosψ，C=3 －4cosψ，D=1 －5cosψ +4cos2ψ，argsh是反双曲正弦函数。海底地形与重力异常之间函数关系建立后，根据拟牛顿法，海底地形迭代计算模型为:

式中，hk为第k次迭代计算结果，h0为初始模型值，Chh为初始模型先验协方差矩阵，A为(1)式的线性化设计矩阵，E为观测数据误差矩阵，一般为对角矩阵，d为观测数据向量，可以包括重力异常、大地水准面、船测海深等多种数据，f(hk－1)表示对初始模型进行非线性运算，函数f将海深模型参数与观测值联系起来。

1.2 频域法

根据Parker公式，在仅顾及一次项的情况下，海底地形起伏与重力异常之间的关系为:

式中，ΔG(k)为反演波段内重力异常的傅里叶变换，ρc、ρw分别为洋壳和海水密度，dw为平均水深，H(k)为反演波段内海底地形的傅里叶变换，其他符号意义同前。

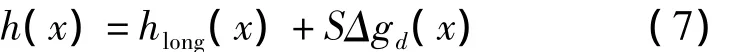
采用频域法联合船测海深和重力异常数据反演计算海底地形模型的最终结果为:式中，h(x)为海底地形计算结果，hlong(x)为船测数据控制的长波海底地形，S为反演波段内海底地形与重力异常之比，Δgd(x)为反演波段内向下延拓至平均水深处的重力异常。

1.3 最小二乘配置法

由重力异常计算海底地形的统计算法模型为［6］:

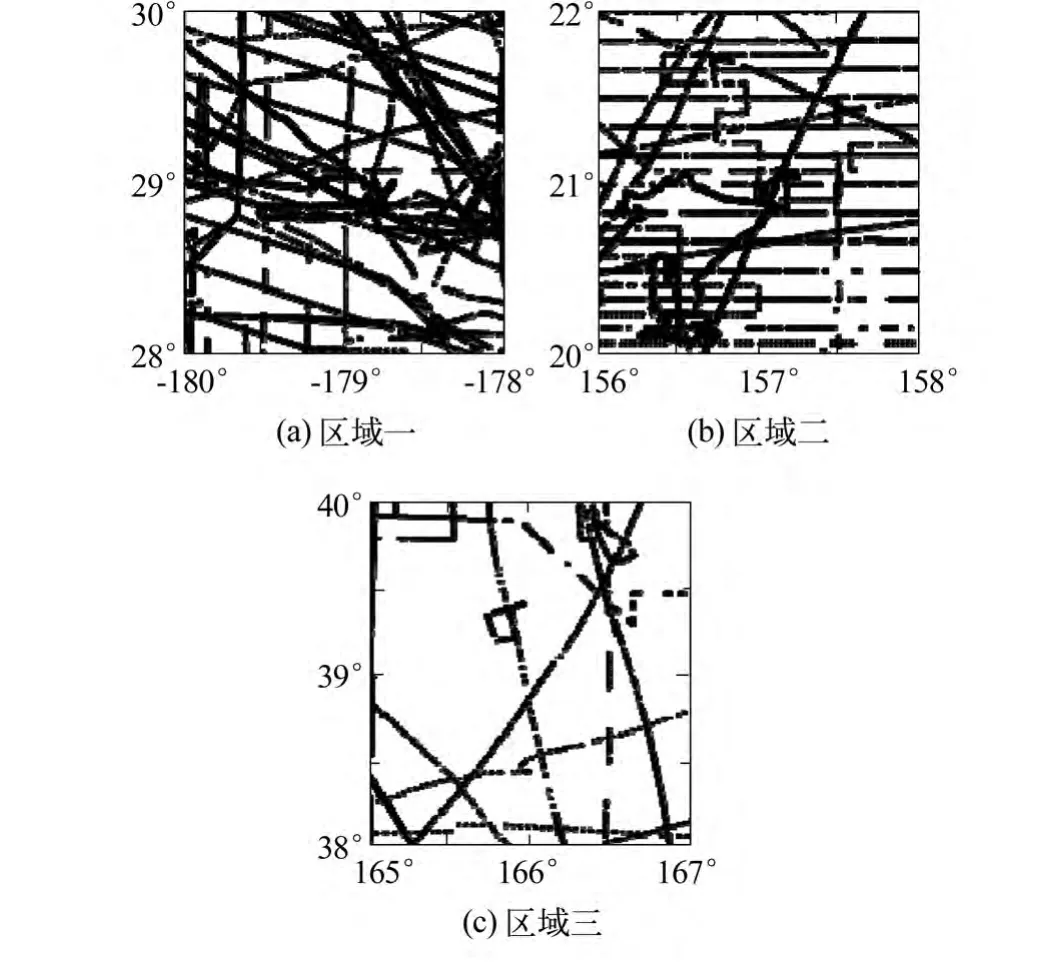
图2 实验区域船测数据分布Fig.2 Distribution of the data of Ship Soundings in the Experimental Areas

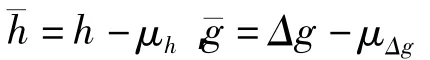
此即为最小二乘配置公式［17］。Hwang［6］阐述了根据海底地形和重力异常的功率谱来估计Chg的方法，以确定配置法中重力异常至海底地形的转换函数。式(9)变为:

形式上，式(10)与频域法式(6)根据均衡原理得到的理论导纳关系类似，但实际意义不同。Zcol(k)基于海底地形和重力异常的统计信息，将地形及重力异常均视为随机信号，无地球物理意义。

2 算例分析

数值计算实验在3个2°×2°区域中进行，区域一范围28°～30°N，178°～180°W，共有 9 092 个船测海深观测值(图2(a));区域二范围20°～22°N，156°～158°E，共有5 199个船测海深观测值(图2(b));区域三范围38°～40°N，165°～167°E，共有 2 548个船测海深观测值(图2(c))。计算中长波海底地形均以船测数据为基础构建，测高重力异常(或重力垂直梯度异常)仅用于计算波长小于200 km部分的海底地形。考虑到实验区域船测数据较少，将其中95%用于计算，另外的5%用于对计算精度的检核。

2.1 空域法计算结果

以船测数据格网化模型作为初始模型，取海底地形先验模型误差和船测海深误差为300 m，测高重力异常误差为5×10－8ms－2，海底地形经验协方差函数参数为0.25°时，根据式(5)仅进行一次迭代计算，即可解得实验区域海底地形(图3)。顾及计算速度和边界效应，每次计算时输入数据范围为0.5°×0.5°，取区域中心4点计算结果为有效值。2°×2°范围内共有14 400个数据点，共需进行3 600次计算，以内存为2 G的笔记本电脑计算，耗时约120 h，计算速度非常慢。

2.2 频域法计算结果

根据频域法，采用重力异常反演计算得到的实验区域海底地形如图4所示。采用FFT算法，完成2°×2°范围数据计算，仅耗时约1 min，计算效率大大优于空域法。

同样，利用垂直梯度异常数据替代重力异常数据，采用30 km短波段截断以抑制高频噪声影响，即对数据进行30～200 km带通滤波后，反演计算的海底地形如图5所示。

2.3 最小二乘配置法计算结果

以本文采用频域法计算的初步结果(图4)为起始模型，采用文献［6］给出的功率谱密度函数法，计算反演波段内的Zcol(k)。为方便应用，以10阶多项式对其进行拟合(图6)。

图6中，红色实线为根据数据计算得到的转换函数，蓝色虚线为10阶多项式拟合结果。总体上，转换函数呈带通滤波形式，即通过对重力异常带通滤波处理，可以将重力异常转换成海底地形。根据图6所示的转换函数，在实验区域内，计算结果如图7所示。

2.4 精度检核

图3 空域法反演结果Fig.3 The bathymetry predicted by Space Domain Method

图4 频域法反演结果(基于重力异常)Fig.4 The bathymetry predicted by Frequency Domain Method(Based on gravity anomaly)

图5 频域法反演结果(基于垂直梯度异常)Fig.5 Bathymetry predicted by the frequency domain method(Based on vertical gravity gradient anomaly)

图6 转换函数Fig.6 Transform function

图7 配置法计算结果Fig.7 Bathymetry predicted by least square collocation method

以船测数据为检核标准，V15.1、ETOPO1、DTU10和GEBCO模型在区域一内精度分别为115.8、234.8、342.1 和 435.7 m;在区域二内精度分别为 65.3、302.7、360.8 和 442.8 m;在区域三内精度分别为 27.8、137.0、188.3 和 180.5 m，4 个模型的精度依次呈下降趋势，V15.1精度最高。3种方法计算结果与船测检核数据之差的统计参数见表1。区域一、二、三的平均水深分别为约4 470、4 520和5 200 m，表1中，相对误差为标准差与平均水深之比。V15.1来自斯克里普斯海洋研究所(SIO)，是采用频域法，联合船测海深和测高重力异常构建的海底地形模型［2－3］;ETOPO1 是美国国家地球物理数据中心(NGDC)于2008年8月公布的全球地形模型［18］;GEBCO模型是在政府间海洋学委员会(IOC)和国际航道组织(IHO)主持下，主要由全球500 m等高距的数字化等深线数据以及船测海深数据，采用格网化方法获得的［19］;DTU10模型是丹麦科技大学(DTU)2010年发布的全球海底地形模型，它基于测高重力异常和GEBCO模型构建，20～120 km波段内海底地形由重力异常反演计算，＞120 km波段海底地形及陆地地形均来自GEBCO模型，相关数据、文档、软件从 DTU 网站(www.space.dtu.dk)获得。

从表1看，在区域一和区域二，空域法计算结果精度优于ETOPO1、DTU10和GEBCO模型，低于V15.1模型，其他方法精度优于DTU10和GEBCO模型，与ETOPO1精度一致;在区域三，空域法计算精度优于DTU10和GEBCO模型，与ETOPO1精度一致，低于V15.1模型，其他方法计算结果精度均略低。

频域法中根据重力垂直梯度异常反演计算的海底地形精度与根据重力异常反演计算的精度一致，说明在实验区域内采用30 km的短波段截断，在抑制重力垂直梯度异常数据高频噪声的同时，没有使计算精度显著降低。

配置法计算精度与频域法根据重力异常计算的精度较为一致，这是因为配置法转换函数计算时采用的参考模型是频域法结果。计算结果说明，配置法计算精度受制于初始模型，为了获得精度较高的计算结果，首先应获得计算区域内较为可靠的海底地形统计信息。

3 结论

1)空域法虽然计算精度较高，但计算速度非常慢，不适用于大区域海底地形模型计算。

2)配置法的关键是计算转换函数，这需要计算海底地形与重力异常之间的相关函数，因而需要预先已知海底地形较准确的统计信息，这与海底地形反演相矛盾，实际中较少采用。

3)频域法依据Parker公式，以船测数据为参考，直接计算海底地形与重力异常之间的线性比例系数，将重力异常转换成海底地形。由于可以采用FFT方法，频域法计算速度很快，精度也较好，是当前常用的海底地形反演方法。V15.1和DTU10模型均采用了此方法。

4)垂直重力梯度异常数据也可用于联合船测海深数据计算海底地形模型，且计算精度与重力异常反演一致。

1 Dixon T H.Bathymetric predictions from SEASAT altimeter data［J］.J Geophys Res，1983，88:1 563 － 1 571.

2 Smith W H F，Sandwell D T.Bathymetric prediction from dense satellite altimetry and sparse shipboard bathymetry［J］.J Geophys Res，1994，99:21 803 －21 824.

3 Smith W H F，Sandwell D T.Global sea floor topography from satellite and ship depth soundings［J］.Science，1997，277:1 956－1 962.

4 Tscherning C C，Knudsen P，Forsberg R.First experiment with improvement of depth information using gravity anomalies in the mediterranean sea［R］.Thessaloniki:Department of Geodesy and Surveying，University of Thessaloniki，1994.

5 Calmant S，Berge-Nguyen M，Cazenave A.Global seafloor topography from a least-square inversion of altimetry-based high-resolution mean sea surface and shipboard soundings［J］.Geophys J Int，2002，151:795 －808.

6 Hwang C.A bathymetric model for the South China Sea from satellite altimetry and depth data ［J］.Marine Geodesy，1999，22:37 －51.

7 黄谟涛.利用卫星测高资料反演海底地形研究［J］.武汉大学学报:信息科学版，2002，27(2):133－137.(Huang M T.The recovery of bathymetry from altimeter data［J］.Geomatics and Information Science of Wuhan University，2002，27(2):133 －137)

8 吴云孙.利用测高重力梯度异常反演中国南海海底地形［J］.武汉大学学报:信息科学版，2009，34(12):1 423 －1 425.(Wu Yunsun.Recovery of ocean depth model of South China Sea from altimetric gravity gradient anomalies［J］.Geomatics and Information Science of Wuhan University，2009，34(12):1 423 －1 425)

9 李大炜.利用卫星测高数据反演中国海及邻近海域海底地形［J］.大地测量与地球动力学，2009(4):70－73.(Li Dawei.Research on inversion of seafloor topography of China Sea and its adjacent areas from satellite altimetric data［J］.Journal of Geodesy and Geodynamics，2009(4):70 －73)

10 胡敏章.利用垂直重力梯度异常反演海底地形［J］.大地测量与地球动力学，2012(5):95－98.(Hu Minzhang.Bathymetry prediction from vertical gravity gradient anomalies［J］.Journal of Geodesy and Geodynamics，2012(5):95－98)

11 Calmant S.Modeling bathymetry by inverting satellite altimetry data:a review［J］.Marine Geophysical Research，1996，18:123 －134.

12 Watts A B.Isostasy and flexure of the lithosphere［M］.Cambridge University Press，2001.

13 Calmant S.Seamount topography by least-squares inversion of altimetric geoid heights and shipborne profiles of bathymetry and/or gravity anomalies［J］.Geophys J Int，1994，119:428－452.

14 Ramillien G，Wright C.Prediction seafloor topography of the New Zealand region:a nonlinear least square inversion of satellite altimetry data ［J］.J Geophys Res，2000，105(B7):16 577－16 590.

15 Parker R L.The rapid calculation of potential anomalies［J］.Geophys J R Astr Soc，1973，31:447 － 455.

16 Wang Y M.Predicting bathymetry from the earth’s gravity gradient anomalies［J］.Marine Geodesy，2000，23(4):251－258.

17 Moritz H.Advanced physical geodesy［M］.Wichmann Karlsruhe，1980.

18 Amante C，Eakins B W.ETOPO1 1 arc-minute global relief model:procedures，data sources and analysis［R］.NOAA Technical Memorandum NESDIS NGDC －24，2009.

19 Goodwillie A M.User guide to the GEBCO one minute grid［R］.2008.

COMPARATIVE ANALYSIS OF METHODS FOR BATHYMETRY PREDICTION

Hu Minzhang1，2，3，4)，Li Jiancheng3)，Xing Lelin1，2)，Zhai Zhenhe5)and Ouyang Mingda5)
1)Key Laboratory of Earthquake Geodesy，Institute of Seismology，CEA，Wuhan 430071
2)Wuhan Base of Institute of Crustal Dynamics，CEA，Wuhan 430071
3)School of Geodesy and Geomatics，Wuhan University，Wuhan 430079
4)Key Laboratory of Geospace Environment and Geodesy，Ministry of Education，Wuhan 430079
5)Xi’an Institute of Surveying and Mapping，Xi’an710054

Three methods of bathymetry prediction:Space Domain Method，Frequency Domain Method and Least Square Collocation Method were compared by actual bathymetry calculating for three experimental areas.The results show that the accuracy of Space Domain Method is slightly better than the others，the calculation efficiency is much lower and not suitable for bathymetry predicting over a large area，however.Frequency Domain Method can be used to calculate bathymetry model quickly by FFT algorithm，and accuracy is acceptable.Detailed statistics information of the bathymetry is needed for bathymetry inversion with Least Square Collocation Method.This is contradicted with the purpose of bathymetry predicting.The bathymetry models for the experimental areas were calculated with Frequency Domain Method combined with the vertical gravity gradient anomaly and the data from ship sound-ings.The result indicates that it is possible to predict bathymetry wiyh vertical gravity gradient anomalies.

bathymetry;gravity anomaly;method in the space domain;method in the frequency domain;leastsquares collocation

P229.1

A

1671-5942(2014)05-0011-06

2013-11-09

中国地震局地震研究所所长基金重点项目(IS201326125);国家测绘地理信息局测绘基础研究基金项目(13－01－01);国家自然科学基金项目(41204019，41304003)。

胡敏章，男，1985年生，博士，助理研究员，研究方向为海底地形与重力均衡。E－mail:huminzhang@126.com。