一种无需模型参数的无线传感器网络定位算法*

张 鹏 冯 欣 周建国 邹进贵

1)武汉大学测绘学院，武汉 430079

2)精密工程与工业测量国家测绘地理信息局重点实验室，武汉 430079

一种无需模型参数的无线传感器网络定位算法*

张 鹏1，2)冯 欣1)周建国1)邹进贵1，2)

1)武汉大学测绘学院，武汉 430079

2)精密工程与工业测量国家测绘地理信息局重点实验室，武汉 430079

提出一种无需模型参数的RSSI定位算法(二重消元法)。该算法通过对传播模型的处理，消去模型参数，并结合截断奇异值分解法求解方程组，实现节点实时定位，减少了传统RSSI定位技术的测试开销。仿真结果显示，二重消元法在一定程度上可以提高定位精度，适用于模型参数未知或不断变化的应用场景。

无线传感器网络;节点定位;RSSI;二重消元法;TSVD

无线传感器网络(wireless sensor network，WSN)是由具有感知能力、通信能力、计算能力的传感器节点以无线形式构成的自组织网络［1］，而节点定位技术作为目标监测与跟踪等众多应用的基础，已成为近年来位置感知领域的研究热点。目前，无线传感器网络大多采用基于接收信号强度指示(received signal strength indication，RSSI)的测距定位技术，其定位性能与信号传播模型密切相关。文献［2－3］提出的曲线拟合建模和多元线性回归建模法，均依赖于定位前实验现场的采样数据，不适于临时部署、快速定位或无法离线建模的场景，如毒气检测、火场救援等。另外，在复杂环境中，通过少量采样数据获取的模型参数不一定准确。文献［4］提出一种无线信号传播模型线性化法，实现了不依赖模型参数的目标定位，但定位精度较差。文献［5－6］通过参考节点间的距离和信号强度实地计算模型参数，但不适于参考节点无法通信的网络。针对上述问题，本文提出一种无线信号模型消元法(简称二重消元法)。通过对信号模型的处理，结合截断奇异值分解法(truncated singular value decomposition，TSVD)计算节点坐标，不依赖于具体环境的模型参数。仿真结果表明，二重消元法能在一定程度上提高定位精度。

1 RSSI测距模型

基于RSSI的测距技术是通过测量信号从发射端到接收端的衰减来计算节点间的实际距离［7］。本文采用 Shadowing理论模型［8］:

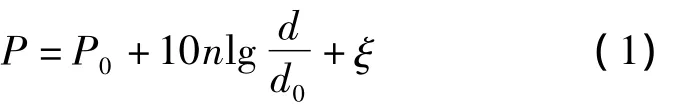
式中，d0为近地参考距离，P0是距离为d0时的接收信号强度，d为距发射端的真实距离，P是距离为d时的接收信号强度。ξ为遮蔽因子，n是路径损耗指数，其数值取决于无线信号的传播环境。由于在实际环境中ξ是均值为0、标准差为σ的正态随机变量，为了简化，将ξ的影响忽略，选用以下模型:

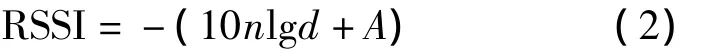
其中，参数A被定义为用dBm表示的距离发射节点1 m处的平均接收信号强度，RSSI为距发射节点d处的接收信号强度。模型参数A、n直接影响到RSSI测距精度，因此在模型参数无法获取或取值不准确的情况下，RSSI定位算法的定位精度可能受到很大影响。

2 二重消元法

2.1 二重消元法原理

通常情况下，基于RSSI测距的定位算法需获取距离信息后才能实现定位，而模型参数的取值是利用信号模型计算距离的关键因素，因此这类算法无法适用于模型参数未知的特殊场合。此外，由于定位环境中存在大量的反射、散射、绕射现象，通过事先采样建立的信号传播模型并不一定准确。这样不仅增加测试开销，获取的精度也不高。二重消元法在一定程度上解决了这些问题。

图1 节点分布图Fig.1 Distribution of nodes

如图1所示，设定位场景中有N个参考节点(N≥4)，位置坐标依次为(x1，y1)，(x2，y2)，(x3，y3)，…，(xN，yN)，未知节点个数为M，P为其中的一个未知节点，坐标为(x，y)。P到各参考节点的RSSI依次为(R1，R2，…，RN)，相应地到各参考节点的距离依次为(d1，d2，…，dN)。当采用简化的测距模型时，对于每个未知节点(如P)，有如下方程式:

将式(3)中的第一式分别与其后的方程式相减，即可消除参数A:

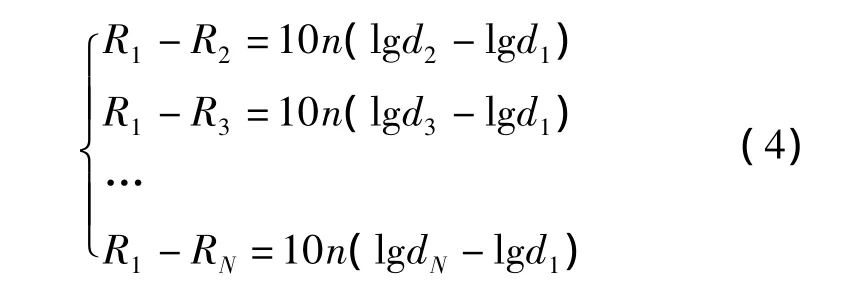
将处理后的方程组中的第一式再与其后的方程式相除，即可消除参数n:

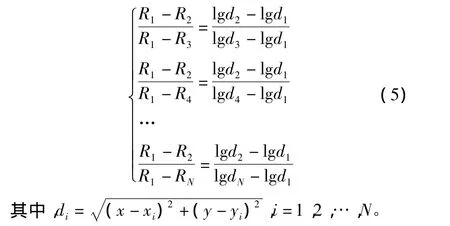
求解非线性方程组(5)，未知参数为待定位节点的坐标(x，y)。将式(5)中的方程式转换后，选用泰勒级数展开迭代法进行求解，并忽略高阶项，(x0，y0)是未知节点P的初始坐标。

令(x0，y0)=(x0+ Δx，y0+ Δy)，代入原方程式继续求解。反复迭代，直到Δx、Δy满足预先设定的门限ε为止，此时(x0，y0)即是未知节点的最终估计坐标。其中，节点的初始坐标可采用加权质心法获取。为了防止迭代收敛过慢损耗节点能源，在程序中设定了迭代次数的上限(实验中设为50次)。

2.2 TSVD求解方程

由于RSSI数据易受环境因素的干扰，为了避免测量误差在矩阵求逆过程中放大，影响定位精度，本文利用截断奇异值分解法(TSVD)［9］求解未知向量X，以解决方程解算中的病态问题。过程如下:

假设矩阵Bm×n(m≥n)的秩为r，那么其奇异值满足σ1≥…≥σr＞σr+1=…=σn=0。变量Σ是一个降阶的含有非负元素的对角矩阵，与矩阵B具有相同的维数，即 Σ =diag(σ1，…，σr)。矩阵 U、V 是正交矩阵，U=［u1，…，um］∈Rm×m，V=［v1，…，vm］=(vik)∈Rn×n，则矩阵B的广义逆、向量X的广义逆解如下:

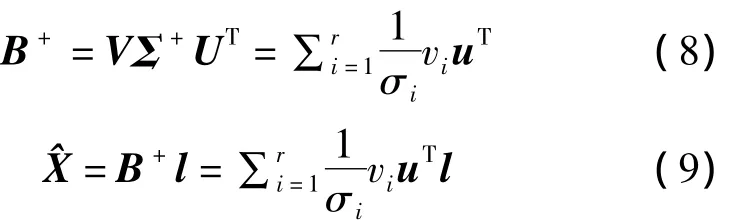
当奇异值σi异常小时，解的计算不稳定并且方差很大，从而导致估算值与准确值相差甚远。TSVD通过舍弃较小的奇异值，有效地解决矩阵求逆中计算结果不准确或发散的情况，更好地表达矩阵的本质信息，抑制噪声的影响。设q为应截断的奇异值个数，此时 Σr－q=diag(σ1，…，σr－q)，则截断奇异值分解得到的参数解为:

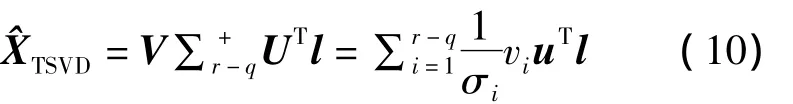
选取截断参数q的方法［5］是:设定参数κ，κ为前r－q个奇异值之和与r个奇异值总和的比值，当κ约等于某一具体数值时，所对应的q即为截断参数的取值。κ的具体数值将在实验部分讨论。

3 仿真及分析

本文用MATLAB对二重消元法进行仿真分析，并与相关算法进行比较。仿真区域设置为50 m×50 m，锚节点数目为5，指定分布在定位场景内。未知节点数目为100，均匀分布，如图2所示。由于二重消元法无需模型参数，即参数的选取对定位结果影响不大，因此测试数据中设定A=－30，路径损耗指数n=3，以便实验仿真。以下所有仿真实验均运行10 000次，取平均值作为最后结果。

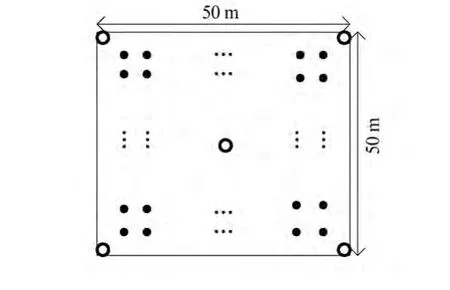
图2 定位场景图Fig.2 Site of locating

3.1 参数κ的取值

首先要探讨二重消元法中TSVD解算阶段的参数κ，其取值与截断参数q及向量X的最终结果密切相关。表1、表2分别显示了κ取不同数值时的定位精度及定位率。从定位精度的角度来看，当环境噪声较小时，奇异值矩阵中的不可靠成分较少，κ取值越大，保留的可靠成分越多，定位精度越高;当环境噪声较大时，矩阵中不可靠成分较多，κ取值相对越小，截掉的不确定成分越多，定位精度相应越高;当环境噪声不大不小时，κ取值较小可能会删除可靠成分，κ取值较大可能仍保留较多的不可靠成分，此时κ取值适中的定位结果最好。从定位率的角度来看，κ取值越小，定位率越高。结合定位环境特性，同时从表1中可看出，当κ≥0.80时，定位精度相差不大;从表2中看出，当κ=0.80时，随噪声变化的定位率等于或接近于100%。因此，二重消元法中选取κ=0.80，来实现定位精度和定位率的折中。

3.2 算法比较

针对不同的环境噪声，比较二重消元法(κ=0.80)、文献［4］中的线性化法及最大似然法，其中最大似然法使用的模型参数跟设定参数大小相同，即在仿真中最大似然法只受到环境噪声的影响，达到最大似然定位的最佳情况。此外，κ=0.80时，定位率在环境噪声较大时只是接近于100%，见表2。在计算平均定位误差时，对于二重消元法中计算发散的点，另两种算法不将其计入平均定位误差内。

从图3可知，当环境噪声较小，如σ=1时，最大似然法和二重消元法的定位精度相近，远优于线性化法。随着环境噪声的增大，3种定位算法的定位误差都不断增大，但二重消元法的增长幅度明显小于最大似然法，线性化法的增长幅度最小，但该算法的定位精度很差。因此，利用二重消元法进行节点定位可以在降低测试开销的情况下有效地提高定位精度。但在环境噪声很大时，二重消元法可能会有少量的节点无法定位。如何提高这种场景下算法的收敛性是今后要研究的重点内容。

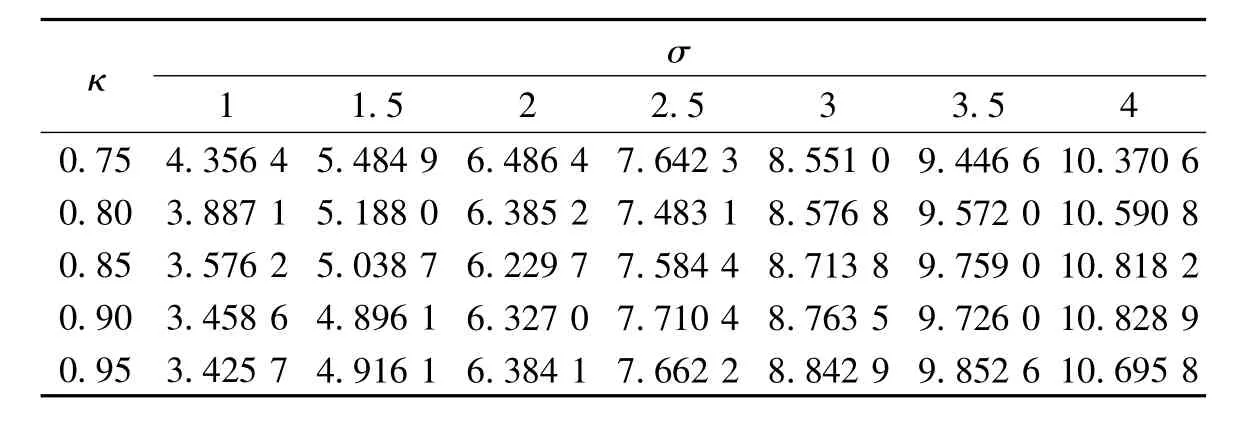
表1 不同κ、σ下的定位精度Tab.1 Locating accuracy under different κ、σ

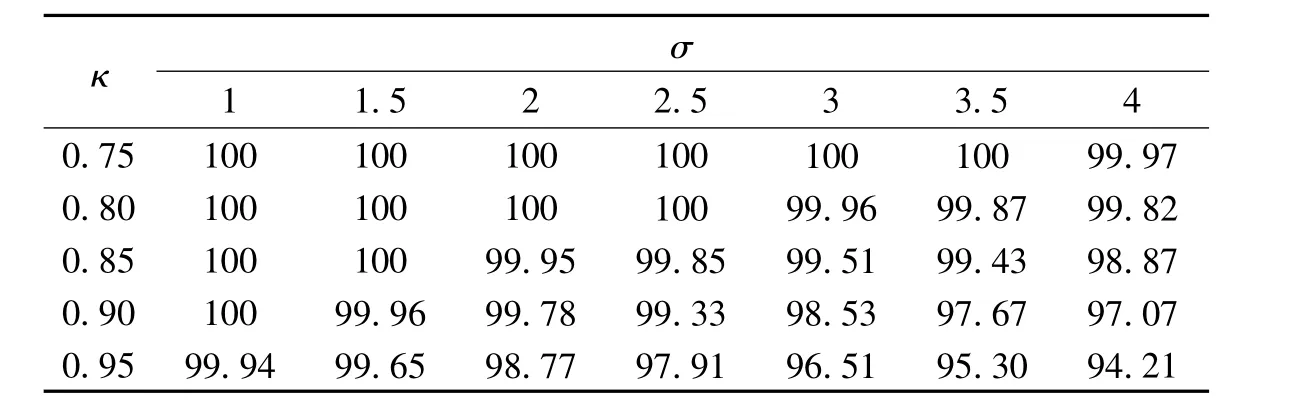
表2 不同κ、σ下的定位率(单位:%)Tab.2 Locating rate under different κ、σ

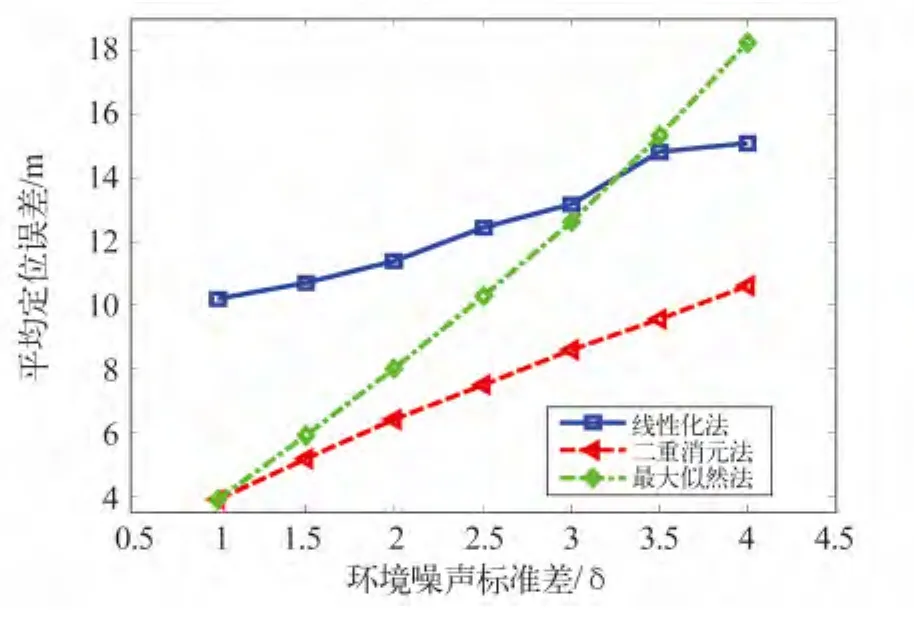
图3 3种算法的定位精度比较Fig.3 Accuracy comparison of three kinds of algorithms

在二重消元法定位率为100%时，进一步分析3种算法的平均定位误差累积分布。这里选取环境噪声不大不小的情况(σ=2.5)来讨论。

图4、图5分别描述了σ=2.5时3种算法的平均定位误差累积分布及每个未知节点的误差大小。从图中看出，二重消元法定位误差较小的节点比例明显要多，相较于另外两种算法而言，大部分节点总是取得最优的定位结果。对于一些无需精确坐标的位置服务场景，二重消元法能较好地实现定位。

4 结语

本文针对基于RSSI的无线传感器网络定位中建模参数的问题，提出了二重消元法。该算法对信号传播模型进行消元处理，结合TSVD理论，能够使用实时测量的RSSI值动态地估计节点位置。从仿真结果可知，二重消元法不但可以避免事先建模所需的测试开销，还可以在一定程度上提高定位精度，在无法获取模型参数或不断变化的特殊场合具有很大的优势。由于在噪声很大的场景中该算法的定位率并没有达到100%，下一步希望在算法模型的解算阶段结合正则化理论，来提高算法的鲁棒性和收敛性。

图4 平均定位误差累积分布(σ=2.5)Fig.4 Distribution of cumulated mean locating error

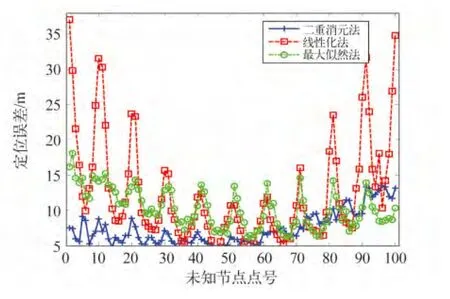
图5 未知节点定位误差比较Fig.5 Comparison of locating error for unknown nodes

1 孙立民，李健中，陈渝，等.无线传感器网络［M］.北京:清华大学出版社，2005.(Sun Limin，Li Jianzhong，Chen Yu，et al.Wireless sensor network［M］.Beijing:Tsinghua University Press，2005)

2 方震，赵湛，郭鹏，等.基于RSSI测距分析［J］.传感技术学报，2007(11):2 526 － 2 530.(Fang Zhen，Zhao Zhan，Guo Peng，et al.Analysis of distance measurement based on RSSI［J］.Chinese Journal of Sensors and Actuators，2007(11):2 526－2 530)

3 袁正午，邓思兵，李恭伟.基于多元线性回归快速迭代的室内定位方法研究［J］.计算机应用研究，2007(12):121－122.(Yuan Zhengwu，Deng Sibing，Li Gongwei.New indoor positioning method based on multiple linear regression iteration［J］.Application Research of Computers，2007(12):121－122)

4 Koo J，Cha H，Localizing WiFi access points using signal strength［J］.Communications Letters IEEE，2011，15(2):187－189.

5 Lim H，Kung L C，Hou J C，et al.Zero-configuration，robust indoor localization:theory and experimentation［C］.IEEE Infocom’06，2006.

6 周建国，张鹏，冯欣.自适应无线传感器网络室内定位算法［J］.大地测量与地球动力学，2012，32(2):74 －77.(Zhou Jianguo，Zhang Peng，Feng Xin.Adaptive algorithm for wireless sensor network indoor positioning［J］.Journal of Geodesy and Geodynamics，2012，32(2):74 －77)

7 安德烈·戈德史密斯.无线通信［M］.北京:人民邮电出版社，2007.(Goldsmith A.Wireless communicatio［M］.Beijing:People Post Press，2007)

8 Patwari N，Ash J N，Kyperountas S.Locating the nodes:cooperative localization in wireless sensor networks［J］.Signal Processing Magazine IEEE，2005，22(4):54 －69.

9 Ke C，Qingming G.TSVD regularization in GPS multicorrelator multipath estimation［C］.Artificial Intelligence，Management Science and Electronic Commerce(AIMSEC)，2011.

NODE LOCATING IN WIRELESS SENSOR NETWORK WITHOUT A PRIOR KNOWLEDGE OF CHANNEL MODEL PARAMETERS

Zhang Peng1，2)，Feng Xin1)，Zhou Jianguo1)and Zou Jingui1，2)
1)School of Geodesy and Geomatics，Wuhan University，Wuhan 430079
2)The Key Lab of Precise Engineering and Industry Surveying，NASMG，Wuhan430079

A RSSI algorithm without a prior knowledge of channel model parameters for node locating in Wireless Sensor Network was proposed in the paper.It can be realized using the algorithm real-time location estimation by coping with the channel model and TSVD to solve the equation.Extensive simulation results show that locating accuracy using the algorithm is higher than some of other RSSI algorithms，and the algorithm is especially suitable to the cases of absence or incorrectness of the channel model parameters.

wireless sensor networks;node localization;RSSI;double-elimination algorithm;TSVD

P228

A

1671-5942(2014)05-0174-04

2013-05-04

国家自然科学基金项目(41074025);高等学校博士学科点专项科研基金项目(20110141120046)。

张鹏，讲师，主要研究方向为无线传感器网络室内定位、压缩感知理论和软件接收机等。E－mail:pzhang@sgg.whu.edu.cn。