地球重力场球冠谐模型的分层构造和分析*

王 燚 姜效典

(中国海洋大学海洋地球科学学院，青岛 266100)

地球重力场球冠谐模型的分层构造和分析*

王 燚 姜效典

(中国海洋大学海洋地球科学学院，青岛 266100)

根据球冠谐系数与点质量模型的关系，提出一种基于多层点质量模型分层构造球冠谐系数的方法。以32°N～34°N，102°E～104°E为计算区域，利用EGM2008模型和实测观测值构造三层球冠谐模型系数，逼近该区域的重力异常场。结果表明，使用本方法构造的球冠谐模型和实测观测值的误差平均值小于0.5×10－5ms－2，当拟合区域的球冠半角为 0.71°时，模型的内符合精度为 ±4.65 ×10－5ms－2。

球冠谐和分析;EGM2008模型;点质量模型;迭代算法;病态性

EGM2008模型通过球谐函数可以较好地描述全球重力场，但在局部重力场描述上，球谐函数不能满足局部重力场的边界条件，对局部重力场的描述只是理论上的一种近似［1］。Haines等［2］指出了运用球冠谐展开逼近局部重力场的可能性。Hwang［3］使用球冠谐理论针对海面地形进行研究;张勤等［4］推导了球冠谐分析法逼近区域地壳垂直形变场的模型;李建成［5］运用球冠谐理论建立我国的局部重力场模型，都取得比较满意的结果。然而在球冠谐系数计算过程中，当观测数小于待求参数时，基函数组成的求解球冠谐系数的矩阵是秩亏的，当观测数远远多于待求的球冠谐系数时，矩阵的条件数比较大，求逆运算的结果不稳定。为了克服该问题，本文引入点质量模型，利用逐级余差思想，分层计算残差重力异常对应的球冠谐系数，并通过系数叠加获得重力场的球冠谐模型。

1 球冠谐系数的点质量模型

点质量模型是地球重力场的一种数值逼近方法。Paul［6］和 Sunkel等［7］对点质量模型的构建作了深入研究。根据 Keldysh-Lavrentiev 定理［8－9］，扰动位可以用球外的一个调和函数逼近。设虚拟场的点质量mi(i=1，2，…，N)分布在一个半径为RB的Bjerhanmmar球层上，由位叠加原理，点质量的扰动场源在边界上产生的扰动位可表示为:

式中，G是万有引力常数，lpi是计算点P到点质量mi的距离。根据第三类边值问题的边界方程［10］，地面上观测点的重力异常值为:

根据非整阶勒让德函数的加法公式［11－12］，球冠外点P到球冠点Q距离的倒数的展开式为:

2 使用迭代法构造球冠谐系数

设地面上有一系列重力异常观测值ΔG={…，Δgj，…}T(j=1，…，M)，根据第三类边值问题，球冠谐重力异常计算公式为:

式中(θj，λj)是球冠上第j个点的余纬和经度，是第j个点的重力异常观测值。应用式(9)、(10)，使用迭代方法计算球冠谐系数CS的计算步骤如图1所示。

图1 迭代法计算球冠谐系数Fig.1 Spherical cap harmonic coefficient calculated by using the iterative method

3 球冠半角与点质量密度和埋藏深度的关系

Bowin［16］利用等效质点模型，给出球谐阶数 n与点质量埋藏深度的关系式为H=R/(n－1)。由球冠谐阶数lk和球冠半角α的关系式lk=90°(k+0.5)/a－0.5，得球冠半角与点质量最大埋藏深度的关系为 H=R/(90°(k+0.5)/a －0.5 －1)。与球谐阶数类似，球冠谐阶数能够拟合的网格间距最小为Δθ=180°/lk。选择北纬31.5°～34°，东经102°～104.5°区域，球冠半角约 1.76°的覆盖范围作为数值计算区域，选取球冠谐阶数k=20，计算得lk=1 047.8，因此点质量模型的最小网格分辨率为Δθ=0.17°。使用EMG2008模型计算网格分辨率分别为0.1°×0.1°、0.2°× 0.2°、0.5°×0.5°和 0.8°×0.8°的180阶重力异常观测值，选取点质量的网格分辨率与重力异常网格分辨率一致，埋藏深度从1 km到80 km，使用迭代法计算球冠谐系数，得到不同网格分辨率下的重力异常误差的均方根如图2和表1所示;点质量求解系数矩阵A的条件数如图3和表2所示。

可以看到，当点质量网格分辨率小于0.17°时，随着点质量埋藏深度的增加，其求解系数矩阵A的条件数迅速上升。虽然重力异常误差均方根在埋深25 km 时达到最小0.08 ×10－5ms－2，但这时求解系数矩阵A的条件数是13 894，矩阵A是病态的，其求逆运算结果不稳定。当埋藏深度小于15 km时，求解系数矩阵A的条件数小于200，其求逆运算结果稳定，与文献［17］结论一致。当点质量网格分辨率大于0.17°时，求解系数矩阵A的条件数增长缓慢，而且不同埋藏深度下对应的重力异常误差均方根 都小于0.01 ×10－5ms－2。因此在给定球冠半角和阶数的条件下，当点质量网格分辨率小于最小间距时，点质量的埋深应当选取与重力异常观测网格分辨率相当的尺度。当设置的点质量网格分辨率大于最小间距时，在点质量一定埋深范围内，其求解系数矩阵A的条件数增长缓慢，所以能根据数据拟合需要设置合理的埋藏度，并保证迭代算法收敛。

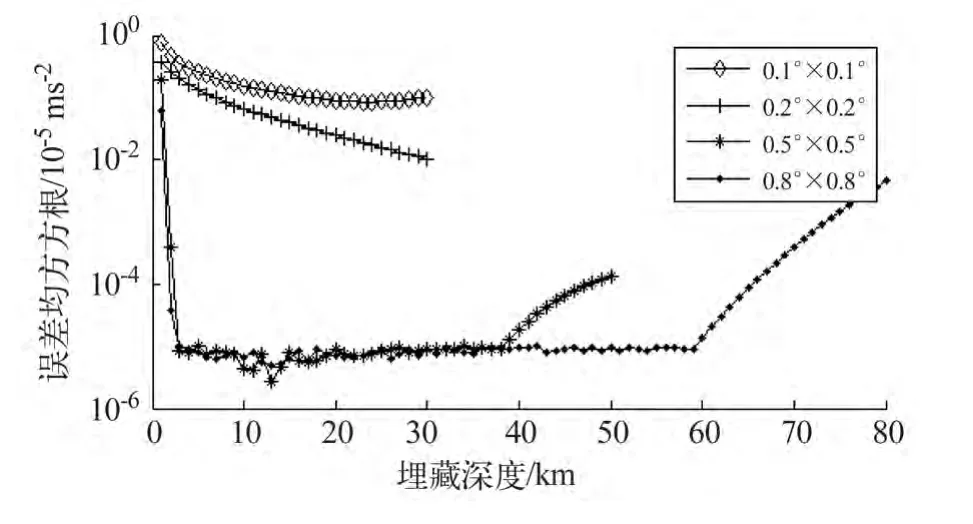
图2 重力异常误差均方根(单位:10－5ms－2)Fig.2 RMS errors of gravity anomaly(unit:10 －5ms－2)

图3 矩阵A的条件数Fig.3 Condition number of matrix A

表1 重力异常误差均方根(单位:10－5ms－2)Tab.1 RMS errors of gravity anomaly(unit:10 －5ms－2)

表2 不同埋藏深度下矩阵A的条件数Tab.2 Condition numbers of matrix Ain different buried depth

4 应用点质量组模型构造三层球冠谐系数

使用点质量组模型分层构造球冠谐系数可以有多种组合，本文将虚拟球层设置在上地幔、壳幔交界处和地壳中，相应地将点质量分为A、B、C 3组模型，其埋藏深度分别设置为93、55和8 km。根据分析，选取31.5°N ～34°N，102°E ～104.5°E 为覆盖区域计算球冠谐模型。这里位于四川和甘肃交界，地势复杂，海拔落差大，西部地形以褶皱系为主，地壳厚度50～72 km，东部以台干为主，地壳厚度38～50 km。因为壳幔密度的差异，低频重力场变化显著［18］。实测重力异常观测值分辨率为3'×3'网格，插值出网格分辨率为1°×1°、20'×20'和3'×3'的重力异常。设置球冠谐半径为1.76°，点质量网格分辨率与重力异常观测值一致，为1°×1°、20'×20'和3'×3'网格分辨率。通过点质量组解算得到三层球冠谐系数，具体计算过程如下。

1)在覆盖范围内使用EGM2008模型生成180阶次位模型重力异常值，然后使用迭代算法计算180阶次位模型对应的球冠谐系数，记为。

5)将4组球冠谐系数叠加得到重力异常观测值的球冠谐模型。用上述方法解算出的球冠谐系数CAS，CBS和CCS，分别计算与之对应的3'×3'网格分辨率残差重力异常值如图4。

图4(a)是球冠谐系数CAS对应的残差重力异常，(b)是球冠谐系数CBS对应的残差重力异常，(c)是球冠谐系数CCS对应的残差重力异常，可以看到3层球冠谐模型能够从低频到高频逐步逼近地球重力场。

在给定球冠半角的条件下，球冠谐阶数决定了能够描述的重力场最小波长［19－20］。三层球冠谐模型的内符合精度是利用实测重力异常观测值与球冠谐模型计算值之差来衡量的。下面给定不同的球冠半角，对应的重力异常覆盖范围如表3。选取球冠谐阶数 k=10，12，14，16，20，计算得本模型内符合精度如表4。

表3 三层球冠谐模型范围Tab.3 The coverage of three layers spherical cap harmonic model

表4 三层球冠谐模型内符合精度(单位:10－5ms－2)Tab.4 Internal consistency accuracy of three layers spherical cap harmonic model(unit:10 －5ms－2)

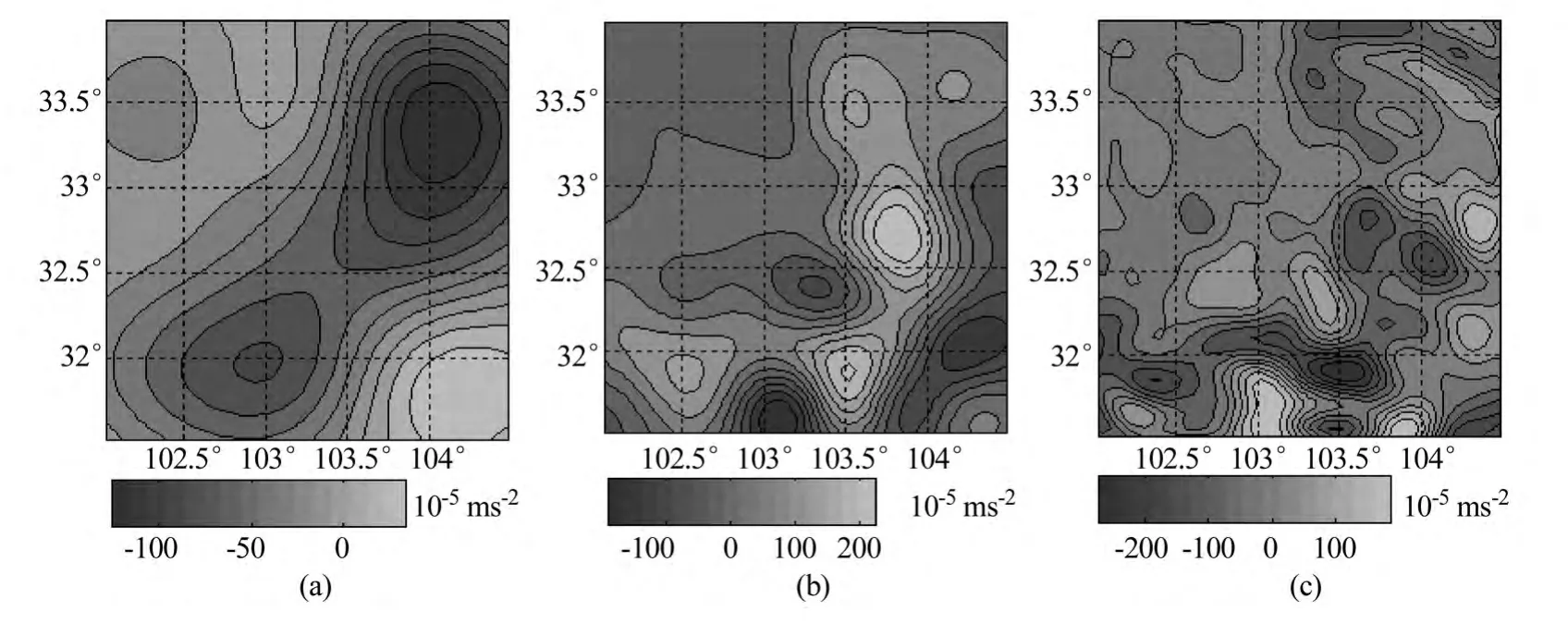
图4 残差重力异常等值线图Fig.4 Contour map of residual gravity anomaly

由表4可以看出，本模型拟合得到的重力异常场精度随着球冠谐阶数的提高而提高;在相同的球冠谐阶数下，拟合的重力异常场范围越小，计算得到的重力异常场精度越高。当球冠谐阶数设置为20阶、重力数据拟合范围的球冠半角为0.71°时，本模型拟合的重力异常场内符合精度最高，均方根误差为 ±4.65 ×10－5ms－2。实测重力异常图和本模型计算的重力异常如图5所示。

图5 实测与模型计算的重力异常Fig.5 Comparison of the gravity anomaly from actual survey and the gravity anomaly computed with spherical cap harmonic model

从实验结果看，通过分层方式构造球冠谐模型，根据不同层点质量分辨率选取合适的埋藏深度，其系数矩阵A稳定性好，保证迭代过程收敛，可以很好地逼近局部地球重力场。

1 彭富清，于锦海.球冠谐分析中非整阶Legendre函数的性质及其计算［J］.测绘学报，2000，29(3):204 －208.(Peng Fuqing，Yu Jinhai.The characters and computation of Legendre functionwith non-integral degree in SCHA［J］.Acta Geodaetica et Cartographica Sinica，2000，29(3):204 －208)

2 Haines G V.Spherical cap harmonic analysis［J］.J geophys Res，1985，90:2 583 – 2 591.

3 Hwang C，Chen S K.Fully normalized spherical cap harmonics:App lication to the analysis of sea 2 level data from TO PEX/POSEIDON and ERS-1［J］.Geophys J Int，1997，129:450－460.

4 张勤，赵超英.地壳垂直形变场逼近的球冠谐分析法［J］.测绘学报，2004，33(1):39 －42.(Zhang Qin，Zhao Chaoying.The spherical cap harmonic analysis methodfor crust vertical deformation field fitting［J］.Acta Geodaetica et Cartographica Sinica 2004，33(1):39 －42)

5 Li Jiancheng.Spherical cap harmonic expansion for local gravity represention［J］.Manuscripta Geodaetica，1995，(20):265－277.

6 Needham P E.The formation and evaluation of detailed geopotential models based on point masses［R］.Ohio:Ohio State University，1970.

7 Sunkel H.The generation of a mass point model from surface gravity data［R］.Ohio:Ohio State University，1983.

8 吴星.卫星重力梯度数据处理理论与方法［D］.郑州:信息工程大学，2009.(Wu Xing.Research on determining the global earth gravity model from satellite gravity gradients［D］.Zhengzhou:Information Engineering University，2009)

9 吴星，张传定，王凯.卫星重力梯度边值问题的点质量调和分析［J］.测绘学报，2011，40(2):213 －219.(Wu Xing，Zhang Chuanding，Wang Kai.Point-mass harmonic analysis of satellite gradiometry boundary value problem［J］.Acta Geodaetica et Cartographica Sinica，2011，40(2):213－219)

10 王建强.重力三层点质量模型的构造与分析［J］.测绘学报，2010，39(5):503 － 507.(Wang Jianqiang.The construction and analysis for three-tier point mass model of gravity［J］.Acta Geodaetica et Cartographica Sinica，2010，39(5):503－507)

11 Hobson E W.The theory of spherical and ellipsoidal harmonics［M］.Cambridge University Press，1931.

12 王竹溪，郭敦仁.特殊函数概论［M］.北京:北京大学出版，1989.(Wang Zhuxi，Guo Dunren.Special functions［M］.Beijing:Peking University Press，1989)

13 Ghadi K A.Transformation of global spherical harmonic models of the gravity field to a local adjusted spherical cap harmonic model［J］.Arab J Geosci，2013(6):375 － 381)

14 王三军.利用球冠谐模型研究GPS水准问题［J］.测绘科学，2008，33(2):13 －14.(WangSanjun.Thespherical cap harmonic analysis of GPS leveling height［J］.Science of Surveying and Mapping，2008，33(2):13 －14)

15 曹月玲，王解先.利用球冠谐分析拟合GPS水准高程［J］.武汉大学学报:信息科学版，2008，33(5):740 －743.(Cao Yueling，Wang Jiexian.Application of spherical cap harmonic analysis to fit GPS level height［J］.Geomatics and Information Science of Wuhan University，2008，33(5):740－743)

16 Bowin C.Depth of principal mass anomalies contributing to the earth’s geoidal undulation and gravity anomalies［J］.Marine Geodesy，1983，21(7):61 －100.

17 吴晓平.局部重力场的点质量模型［J］.测绘学报，1984，13(4):249 － 258.(Wu Xiaoping.Point-mass model of local gravity field［J］.Acta Geodaetica et Cartographica Sinica，1984，13(4):249 －258)

18 高锐.由地震探测揭示的青藏高原莫霍面深度［J］.地球学报，2009，30(6):761 － 773.(Gao Rui.The Moho depth of Qinghai-Tibet plateau revealed by seismic detection［J］.Acta Geoscientica Sinica，2009，30(6):761 －773)

19 王喜臣.利用球冠谐分析方法提取不同波长重力场异常［J］.世界地质，1996，15(3):80 － 83.(Wang Xichen.Extracting different wavelength gravity anomaly by the spherical cap harmonic analysis method［J］.Global Geology，1996，15(3):80 －83)

20 翟振和，孙中苗.渤海湾多源重力数据的自适应融合处理［J］.测绘学报，2010，39(5):444 －449.(Zhai Zhenhe，Sun Zhongmiao.The adaptive fusion of multi-source gravity data in Bohai Gulf［J］.Acta Geodaetica et Cartographica Sinica，2010，39(5):444 －449)

STRUCTURE OF MULTILAYERED SPHERICAL CAP HARMONIC MODEL

Wang Yi and Jiang Xiaodian
(College of Marine Geo-science，Ocean University of China，Qingdao 266100)

According to the relationship between the spherical cap function and the point mass model，a model was proposed based on multilayer point mass model structure coefficient of spherical cap harmonic method.Taking a region(32°N-34°N，102°E-104°E)as the calculating area，the Gravity anomaly was calculated using the three layers spherical cap harmonic coefficient which constructed by EGM2008 model and the Gravity measured observations.Analysis of fitting precision of gravitational field under different spherical cap harmonic order indicates that the average error between the spherical cap harmonic model and the measured observations is less than 0.5 ×10－5ms－2，and internal consistency accuracy of the model is 4.56 ×10－5ms－2when Spherical cap half angle is 0.71°.

spherical cap harmonic analysis;EGM2008 model;point mass model;Iterative algorithm;ill-condition

P312

A

1671-5942(2014)05-0030-05

2014-01-03

海洋公益性项目(201305029-02)。

王燚，男，1974年生，博士，讲师，主要研究方向为地球物理勘探方法与信息技术。E－mail:wyfox009@163.com。