变质量贮箱类流固耦合系统的振动响应及时频特性分析
2014-09-18马驰骋张希农柳征勇胡迪科
马驰骋, 张希农,柳征勇,胡迪科
(1.西安交通大学 机械结构强度与振动国家重点实验室,西安 710049;2.上海宇航系统工程研究所,上海 201108)
随着对火箭运载性能要求的提高,火箭推进剂所占结构的比重不断增大,液体燃料与燃料贮箱的耦合振动对于火箭正常运行的影响越来越大。由于火箭携带的燃料质量大,整体结构频率比较低。而且随着燃料的消耗,系统的总体质量减少,将引起系统振动频率的显著改变,液体燃料消耗对火箭的运动有着显著的影响。另外,研究液体燃料与贮箱结构之间的流固耦合振动,对于火箭飞行性能与飞行安全也有着重要的意义。燃料贮箱在火箭飞行过程中会受到主发动机强烈的振动和冲击影响,除了受到外界载荷的影响外,内部填充的液体燃料也会产生晃荡作用,从而产生外界载荷与内部流固耦合作用共同叠加的效应。近年来,贮箱的动力学研究得到许多航天工作者的重视。许多学者完成了充液容器晃动问题的开创性研究工作,Moiseevp[1]详述了有关充液容器晃动问题的基本理论和文献。Ibrahim等[2]在综述性文章中介绍了关于含液体晃动系统的动力学研究方法及研究进展。国内很多学者针对含液容器中液体的晃动影响也进行了一系列的研究。周思达等[3]介绍了近年来运载火箭贮箱流固耦合系统的分析方法。苟兴平等[4]利用推广形式的驻定压力原理建立了刚-液耦合系统液体晃动的动力学方程,并研究了其动力学特性。包光伟[5]以油罐车为背景,建立了平放柱形贮箱内液体晃动的等效力学模型。刘文一等[6]研究了在升空过程中振动冲击对某姿控发动机双层结构燃料贮箱的影响,利用流固耦合理论,对空载和充液两种条件下的贮箱进行了模态分析、频率响应分析和冲击响应分析。朱琳等[7]将表征液体运动的节点压力缩聚到自由面,利用主坐标表征液体晃动,采用等效Laplace方程的边值问题求解了液固耦合方程组中的附加质量矩阵、附加刚度矩阵和耦合矩阵,分析并获得了推进剂及贮箱的液固耦合振动特性。但是以往的研究者主要研究了液体晃动对系统响应的影响,关于液体减少过程中贮箱的动力学分析的问题开展的较少。
本文中,重点研究了变质量贮箱流固耦合系统的动力学建模及动力学响应分析。考虑到系统的复杂性,采用PATRAN-NASTRAN有限元程序和动力学响应分析的Newmark直接积分法,建立了变质量贮箱流固耦合有限元模型并得到了其响应,并使用SPWVD研究了变质量系统的时频特性。通过比较不同条件下贮箱结构的动力学响应,重点观察了变化的质量对该燃料贮箱的影响。本文提出的建模及动力学仿真方法,可用于处理类似的变质量结构的动力学问题。

图1 含液贮箱示意图Fig.1 A fluid containing tank
1 运动方程
所考察的弹性贮箱动力学模型如图1所示,圆柱形贮箱半径为R,高度为H,充液深度为h(t),是一个随时间减小的函数。假设液体为无粘、无旋、不可压缩的理想流体,则其运动的速度场有势。
针对贮液箱中液体与箱体弹性结构相互作用的复杂性,而现在又面临的变质量的问题,更增加了该流固耦合系统动力分析问题的困难性。为解决该问题,必须对该问题的模型进行简化。其中解决该问题的一种有效的简化方法就是虚拟质量法,即将流体对固体的作用,以固体的附加质量的形式出现。该方法可以有效的化简流固耦合问题,极大的减小工作量,是处理贮液箱问题的一种有效手段。在流固耦合系统中。使用虚拟质量法,通过施加一个附加质量矩阵实现不可压缩流体对结构的作用,考虑流体作用时系统的有限元计算方程[8]为:
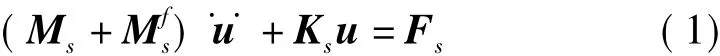
其中Ms和Ks分别为壳体结构的质量矩阵和刚度矩阵,Fs为外载荷矩阵,u和分别为位移向量和加速度向量代表流体对固体的作用,现以结构的附加质量的形式出现,称为附加质量矩阵。流固耦合问题退化为考虑附加质量的固体动力学问题,从而大大简化了流固耦合系统的分析。
基于附加质量理论,NASTRAN采用边界元法得到附加质量矩阵,并称之为虚拟质量法,对于不可压缩、忽略表面自由表面波动的非粘性流体,流体力学的基本方程可以简化为Laplace方程。用Helmholtz边界积分法求解Laplace方程,可以得到流体边界上任意一点ri处的速度向量和压力向量分别为:
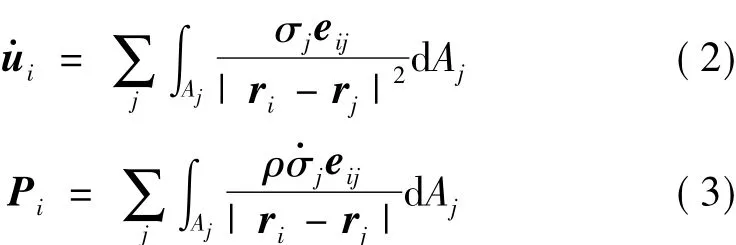
其中σj为流场在点rj处面元Aj上的流体通量,eij为从点j到i的单位向量。ρ为流体的密度。对式(2-3)在结构有限元表面进行积分,得到:
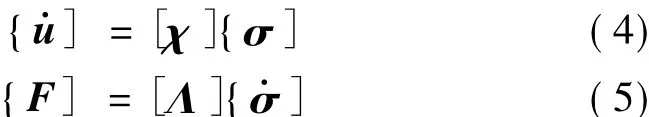
其中矩阵[χ]和[Λ]为积分系数矩阵,F为流体作用在结构上的节点力。同时根据力向量、质量矩阵和加速度向量的关系:

通过式(7),将流体对固体的作用,以固体的附加质量的形式出现。由于一般情况下,水对结构的形成的刚度相对于结构本身的刚度小得多,因此可以忽略,从而得到贮箱结构的动力学方程如式(1)所示。
虚拟质量法避免了流体单元网格的划分,大大简化了建模过程,有利于工程应用。燃料没有消耗即系统的质量不发生改变时,系统的动能和弹性势能可以表示为
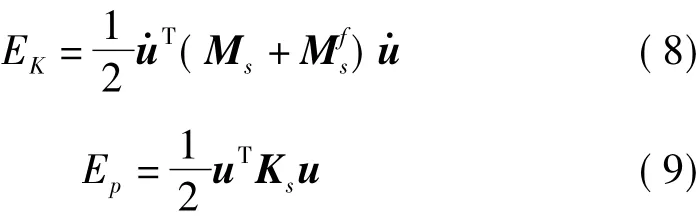
在飞行器飞行当中,燃料的消耗使得附加质量是一个随时间变化的函数,因此当系统的质量变化时,系统的动能可以写为

假设系统的结构阻尼是质量矩阵和刚度矩阵的线性组合,即Rayleigh阻尼:
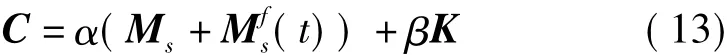
Rayleigh阻尼的比例系数α和β可以根据系统的前二阶横向振动固有频率和模态阻尼比求得。

2 数值仿真
这里采用的模型为一个两端封闭的圆柱壳,使用有限元软件PATRAN-NASTRAN,采用虚拟质量法,对图1所示的贮箱建立有限元模型如图2所示。壳体底面半径为0.2 m,壳体厚度为0.004 m,高度为1 m。有限元网格如下图2所示,共有462个节点和460单元。假设固体结构材料为各项同性材料,弹性模量为71 GPa,泊松比为 0.33,密度为 2 850 kg/m3,贮箱内液体的密度为1 000 kg/m3。支撑弹簧采用BUSH两节点单元,壳体结构采用QUAD4四节点单元。在PATRANNASTRAN虚拟质量法中,在卡片ELIST中定义流固耦合作用面,通过卡片MFLUID定义不可压缩流体的属性,并将液体以附加质量的形式对结构的作用。只有在ELIST/MFLUID卡片中定义的单元才能输出压力,附加质量矩阵的变化随着ELIST/MFLUID卡片中定义的单元的变化而变化。
对节点342处施加一个初始外力,产生一个初始位移,撤去外力后,研究结构的自由振动。在研究当中,只给了系统一个初始的位移,形状与左右摆动振形相似(充满液体时第1阶振形)。图3中给出了建模及仿真分析流程图。其中计算的难点在于构建变质量系统的质量变化函数,由于在计算迭代过程中涉及到变化的质量矩阵和刚度矩阵,计算量比较大,耗时长。使用有限元软件NASTRAN得到系统 t1,t2,t3,…时刻的质量矩阵和刚度矩阵后,采用线性插值的方法得到系统t时刻的质量矩阵和刚度矩阵,使用Newmark直接积分法计算了系统的位移响应,然后使用快速Fourier变换得到了系统的频率响应曲线。
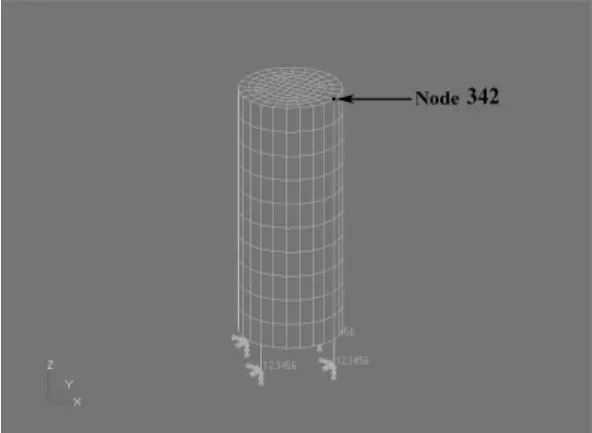
图2 有限元网格Fig.2 Finite element model of a fluid containing tank

图3 计算流程图Fig.3 The flow chart of the calculation
首先计算了不同液面高度时系统的第一阶横向振动固有频率。第一阶横向振动固有频率随壳体中液面高度的变化曲线如图4所示。使用虚拟质量法,在PATRAN-NATRAN中直接计算得到系统的固有频率,如图4中红色线(三角形标记)所示,然后根据PATRAN-NATRAN中提取出的附加质量矩阵,在MATLAB程序中采用插值的方法计算任意时刻系统的固有频率,如图4中蓝色线(圆形形标记)所示。使用PATRAN-NATRAN求解时不变系统的固有频率非常方便,但是处理质量时变系统的瞬态响应比较困难。编写MATLAB程序对PATRAN-NATRAN进行二次开发,是一种简单有效的方法。在飞行器飞行过程中,随着燃料的消耗,贮箱结构的质量减少,但是刚度基本不受影响,因此系统的振动频率会随之增大。第一阶横向振动固有频率从10.171 Hz增大到 34.879 Hz。通过NASTRAN计算得到的结果和编制的MATLAB程序计算得到的结果比较一致,说明了程序的有效性。
前二阶模态阻尼比在这里分别取为0.58%和0.41%。根据贮箱空箱时的固有频率,可以求得Rayleigh阻尼系数 α =2.180 2,β =7.537 1 ×10-6,当贮箱中装满燃料时,根据系统的固有频率可以求得Rayleigh阻尼系数 α =0.67,β =1.732 ×10-5。计算表明,满箱时系统的结构阻尼比空箱时系统的结构阻尼大,因此计算中使用了满箱时系统的结构阻尼比例系数。图5和图6分别给出了系统的自由振动位移响应曲线和振动响应曲线。对比情况1和情况2两种情况下系统的位移响应和频率响应,可以看出,变质量引起的负阻尼对系统的影响非常显著,极大的减缓了系统振动的衰减。特别是在1 s-3.5 s之间,系统的质量变化引起的负阻尼对系统的影响尤为显著。由于系统的质量是变化的,所以系统的振动频率也是随时间变化的。在频谱图上,可以明显看出,与时不变系统不同的是,质量时变系统的频响曲线是由一系列的频率值组成的,振动频率的变化范围与图4中所示的系统的变化范围是一致的,也就是说系统的振动频率的变化范围,可以根据系统质量的变化范围确定。

图4 不同液面高度时系统的第一阶横向振动固有频率Fig.4 Lateral vibration frequency of first order for different liquid level height
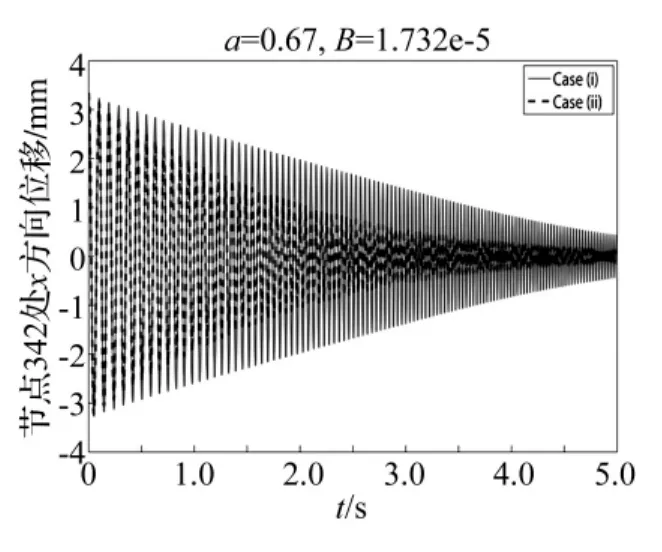
图5 节点342处x方向的位移响应Fig.5 Displacement responses of Node 342 in x direction

图6 节点342处x方向的频率响应Fig.6 Frequency responses of Node 342 in x direction

图7 节点342处x方向的位移响应Fig.7 Displacement responses of Node 342 in x direction
从式(6)中可以看出,变质量引起的阻尼与质量变化率成正比,如果系统的质量迅速减小,那么会产生一个比较大的负阻尼。图5和图6分别给出了系统的自由振动位移响应曲线和频率响应曲线。这里假设系统的质量变化过程只有1 s,在系统的振动中,变化的质量引起了一个非常大的负阻尼。从位移响应曲线和频率响应曲线可以明显看出,t<0.7 s时,负阻尼的使得系统的振幅增大,当t>0.7 s,结构阻尼的作用大于负阻尼的作用,使得系统的振幅衰减。从频响曲线中也可以看出负阻尼使系统的振动振幅增大。
3 时频特性分析
从上面的分析中可以发现,Fourier变换缺乏时间和频率的定位功能,在分辨率上以及对非平稳信号分析具有局限性。而Wigner-Ville分布凭借其优良的时变特性和较高的时频分辨率一直被应用于信号的分析和处理领域。Wigner-Ville分布是Cohen类分布的一种[9-10],是一种双线性的表示时频分布的函数。所谓双线性形式,是指所研究的信号在时频分布的数学表达式中以相乘的形式出现两次。Wigner于1932年首先提出Wigner分布的概念,并把它用于量子力学领域。在之后的一段时间内并没有引起人们的重视。直到1948年,首先由 Ville把它应用于信号分析。因此,Wigner分布又称Wigner-Ville分布,简称为WVD。其表达式如下:

图8 节点342处x方向的频率响应Fig.8 Frequency responses of Node 342 in x direction
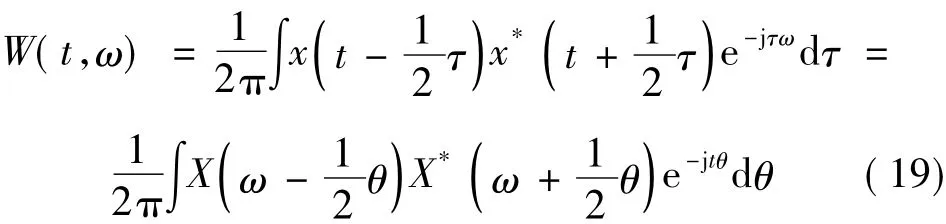
x(t)和X(ω)分别为真实的时域信号和频域信号。*表示函数的复共轭函数。从式中可以看到,由于WVD可以在整个时-频域显示信号的能量分布。Wigner-Ville分布实质上是对信号的瞬时相关函数的Fourier变换,其结果能够反映信号的时频特征。为了减少交叉项,平滑伪Wigner-Ville分布(SPWVD)对时域变量和频域变量同时加窗。其定义为:
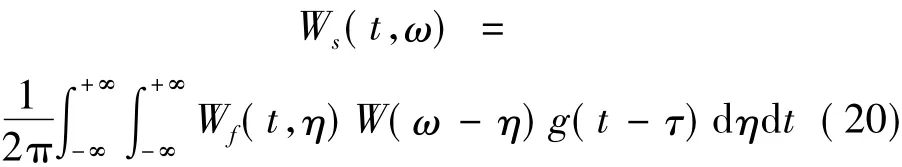
这里的W(ω-η)和g(t-τ)是两个实对称窗口。对信号进行时域频域加窗平滑处理后,时域和频域上的交叉项可以得到很大的抑制。而且时域平滑和频域平滑的尺度容易控制,并且可以独立选择窗函数W(ω-η)和 g(t-τ)的长度[11]。
首先研究了系统质量变化率比较小时的时频响应。对图5中的位移响应曲线做SPWVD,得到了图9和图10中显示的两种情况下节点342处x方向位移的时频响应谱。从图中可以看出任意时间任意频率点系统的振动能量密度。图11和图12给出了系统的系统振动频率随时间的变化谱图,与图2中系统的频率变化曲线是一致的,这是传统的FFT变换无法得到的。

图9 节点342处x方向位移的时频响应谱Fig.9 SPWVD of the displacement of Node 342 in x direction
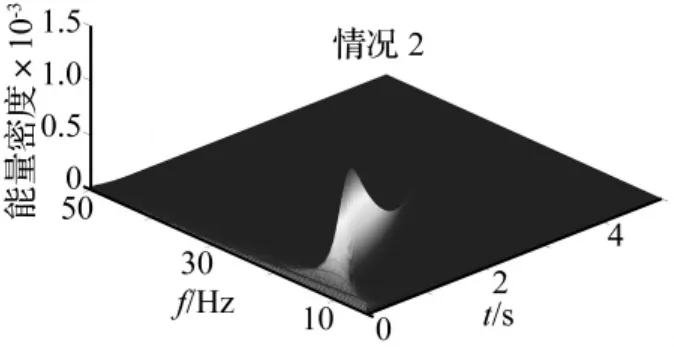
图10 节点342处x方向位移的时频响应谱Fig.10 SPWVD of the displacement of Node 342 in x direction
类似的,对图7中的位移响应曲线做SPWVD,得到了图13和图14中显示的两种情况下节点342处x方向位移的时频响应谱。对比图13和图14可以看出,当考虑负阻尼的作用时,由于负阻尼的作用超于过了系统结构阻尼的作用,使系统的能量增大,从图14中可以看出,系统的结构阻尼在振动中起主要作用,系统的能量随时间减小。图15和图16给出了系统的系统振动频率随时间的变化谱图。
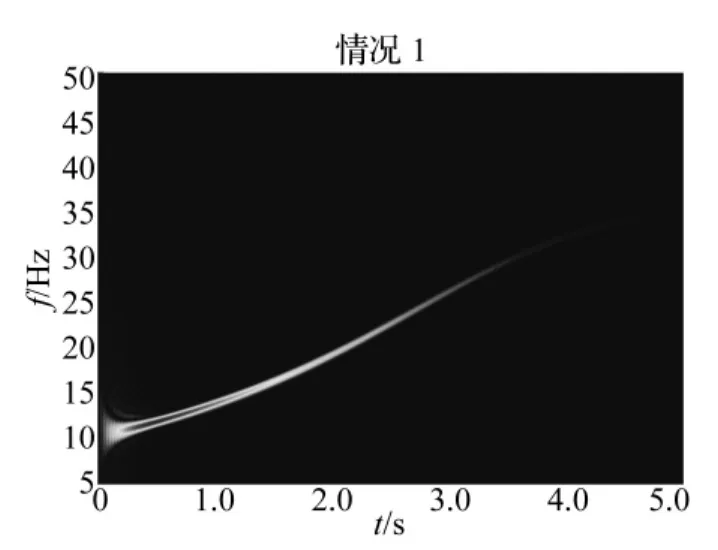
图11 节点342处x方向位移的时频响应谱Fig.11 SPWVD of the displacement of Node 342 in x direction

图12 节点342处x方向位移的时频响应谱Fig.12 SPWVD of the displacement of Node 342 in x direction
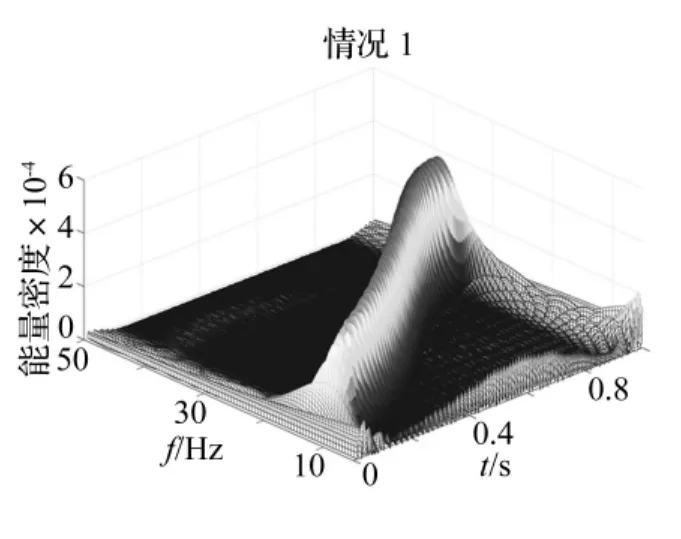
图13 节点342处x方向位移的时频响应谱Fig.13 SPWVD of the displacement of Node 342 in x direction
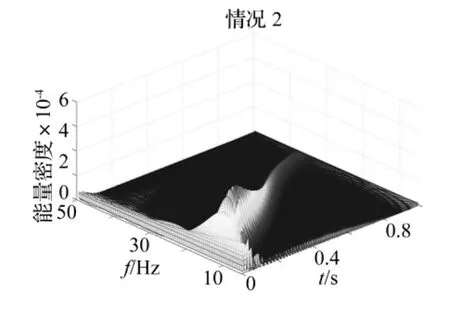
图14 节点342处x方向位移的时频响应谱Fig.14 SPWVD of the displacement of Node 342 in x direction

图15 节点342处x方向位移的时频响应谱Fig.15 SPWVD of the displacement of Node 342 in x direction

图16 节点342处x方向位移的时频响应谱Fig.16 SPWVD of the displacement of Node 342 in x direction
4 结论
基于虚拟质量法,推导了变质量贮箱流固耦合系统的有限元方程,使用NASTRAN-MATLAB建立了变质量储箱的有限元模型,该模型主要考虑了系统的质量变化对系统动力学特性的影响。通过一个附加质量矩阵来表征流体对固体结构的影响,大大简化了建模及数值仿真。有限元方程的解与NASTRAN计算的结果是一致的,说明了这种方法的可行性。
(1)附加质量矩阵与流体的液面高度有很大的关系。由于系统的质量是随时间变化的,因此系统的振动频率也是随时间变化的。振动频率的变化范围可以通过系统质量的变化范围确定。
(2)变化的质量对系统的另外一个影响主要体现在产生了一个附加的阻尼。变质量引起的阻尼与系统的质量变化率有直接的关系,也就是说,系统质量变化越快,产生的负阻尼越大。当系统质量增加时,会产生一个正阻尼,而当系统质量减少时,会产生一个负阻尼。特别需要注意的是,当产生的负阻尼的作用超过了系统本身结构阻尼的作用时,会引起系统振幅的增大。如果变形超出了结构的弹性范围,甚至会造成系统的破坏。
(3)使用Wigner-Ville分布变质量贮箱流固耦合系统的振动信号进行分析,获得了振动信号的时频响应谱。在时频域上研究了非稳态信号的时频特性,通过时频谱图上的能量密度分布,可以观察系统在特定时间特定频率时的振动特性。Wigner-Ville分布是分析非稳态信号的一种有效工具。
[1]Moiseev N N.Introduction to the theory of oscillations of liquid-containing bodies[J]. Advances in Applied Mechanics,1964,8:233 -289.
[2]Ibrahim R A,Pilipchuk V N,Ikeda T.Recent advances in liquid sloshing dynamics[J].Applied Mechanics Review,2001,54(2):133-199.
[3]周思达,刘莉.运载火箭贮箱流固耦合分析方法综述[J].强度与环境,2010,37(3):52 -63.ZHOU Si-da,LIU Li.A review on the analysis methods of fluid-structure coupling for launch vehicle fuel tank[J].Structure & Environment Engineering,2010,37(3):52-63.
[4]苟兴宇,尹立中,马兴瑞,等.窄长方形贮箱中液体的强迫晃动[J].力学与实践,1998,20(4):20-22.GOU Xing-yu,YIN Li-zhong,MA Xiong-rui,et al.Forced sloshing of liquid in a narrow rectangular container[J].Mechanics in Engineering,1998,20(4):20 -22.
[5]包光伟.平放柱形贮箱内液体晃动的等效力学模型[J].上海交通大学学报,2003,37(12):1961 -1968.BAO Guang-wei,Equivalent mechanical model of liquid sloshing in horizontal cylindrical container[J].Journal of Shanghai Jiaotong University,2003,37(12):1961 -1968.
[6]刘文一,李玉龙,吴训涛,等.流固耦合作用下某双层结构燃料贮箱动力学特性分析[J].弹箭与制导学报,2011,31(5):132-134.LIU Wen-yi,LI Yu-long,WU Xun-tao,et al.Analysis of dynamic characteristic of double-deck propellant tank under liquid-solid coupling interaction[J].Journal of Projectiles,Rockets,Missiles and Guidance,2011,31(5):132 -134.
[7]朱琳,唐国安,柳征勇,等.推进剂与贮箱液固耦合振动的动力学分析[J].振动与冲击,2012,31(5):139-143.ZHU Lin,TANG Guo-an,LIU Zheng-yong,et al.Dynamic analysis for fluid-structure coupled vibration of propellants and fuel tank[J].Journal Vibration and Shock,2012,31(5):139-143.
[8] MSC.Nastran advanced dynamic analysis user’s guide[M].Santa Ana.CA 92707 USA:MSC.Software Corporation,2004.
[9] Cohen L.Time-frequency distributions-A review[C].Proc.IEEE,NY USA,1989,77(7):941 - 981.
[10] Hlaswatch F,Boudreaux-bartels G F.Linear and quadratic time-frequency signal representations[J]. IEEE Signal Processing Magazine,1992,4:21 -67.
[11]姜鸣,陈进,汪慰军.几种Cohen类时频分布的比较及应用[J].机械工程学报,2003,39(8):129-134.JIANG Ming,CHEN Jin,WANG Wei-jun.Comparison and application of some time frequency distribution belonging to cohen class[J].Chinese Journal of Mechanical Engineering,2003,39(8):129-134.
