基于多源信息的高速列车走行部故障识别方法

朱建渠，金炜东，郑 高，朱 斌，4

(1.西南交通大学 电气工程学院，成都 610031;2.重庆科技学院，重庆 401331;3.公安海警学院 机电管理系，浙江 宁波 315801;4.长江师范学院，重庆 408100)

高速列车持续的高速运行，会导致列车走行部磨损加快、振动加剧。对高速列车走行部进行有效的故障诊断和识别，是实现及时维护，降低使用维护成本，保证列车运行安全的关键。

对于列车走行部故障特征的研究，目前主要集中在对振动信号的时频分析上，如小波分析法［1－2］、短时傅里叶变换［3］、经验模式分解［4－6］、幅度谱特征［7］等，这些方法都是针对单一传感器、单一故障进行分析。由于高速列走行部车传感器众多，监测数据内容丰富，涉及面广，数据的影响因素多，且相互关联，同一种故障可用不同的特征指标来描述，同一种症状表现往往又是几种故障相互作用的结果。检测量与故障特征之间，故障特征与故障源之间都是一种非线性映射。因此，故障的多样性、不确定性和各种故障之间联系的复杂性构成了故障识别技术上的难点［9］。仅靠单一传感器和单一故障特征量的方法不能综合考虑各方面的因素，造成识别效果不好，难以完成识别任务。比较合理的方法就是采用信息融合技术，进行多传感器、多特征的信息融合识别。

证据理论对于不确定信息有较强的处理的能力，在故障诊断检测、多目标识别、多传感器信息融合、不确定性多属性决策等方面有广泛应用，而mass函数的获得是证据理论得以应用的关键所在［9］。林云等［8］利用灰度关联算法、韩峰等［10］引入了一种置信距离的方法、徐琰珂等［11］利用模糊集合的方法、Xu 等［12］利用证据的信息量来确定各传感器信息的可信度，从而确定出基本概率分配函数，都取得了一定的成果。

本文在前人研究成果的基础上，结合高速列车运行的特点，提出了一种多特征、多信息源融合的故障识别方法。信息融合的过程分为两级，如图1所示。第一级实现不同传感器相同特征的融合:对于每一个传感器的某种特征值，被测故障属于哪种类型的可能性的大小用隶属度来表示，但也可能出现这种情况，不同传感器的同类特征值属于不同故障类型的隶属度不一样，甚至有较大的差异或者矛盾的情况。解决的办法是定义一融合度函数，如某个传感器的某类特征与其它传感器的同类特征融合度高，得到其它传感器的支持，则它的此类特征在融合的过程中的权系数就大，反之权系数就小，这样就得到不同传感器同类特征融合后属于不同故障类型的隶属度。第二级实现不同特征的融合:就是把融合后的同一特征属于不同故障类型的隶属度按比例转换成基本信任分配函数，然后证据理论的融合规则进行融合，进而判断出故障的类型。

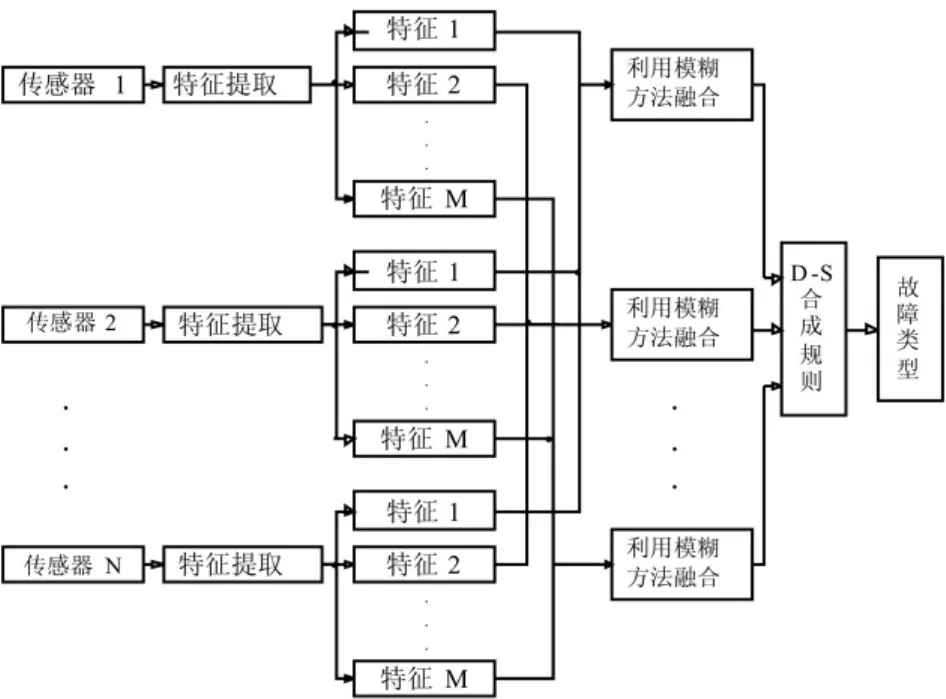
图1 两级信息融合示意图Fig.1 Schematic diagram of two level information fusion

1 不同传感器相同特征的信息融合

1.1 融合度函数

设有N个传感器，从每个传感器测得的数据中提取M个特征，故障类型有K类，对于某类特征不同传感器的属于各故障类型的隶属度函数可表示成如下矩阵形式:

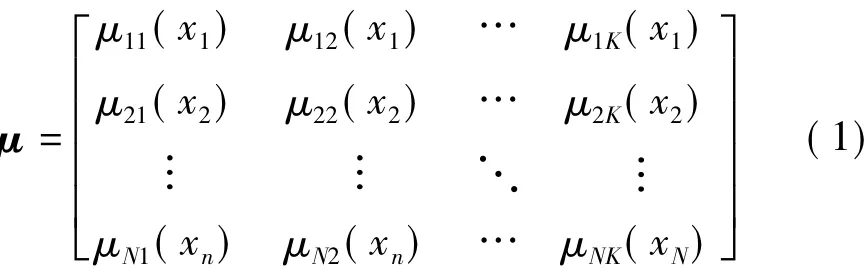
式中，μNK(xN)表示第N个传感器的某类特征属于第K类故障的隶属度函数。

第i个传感器和第j个传感器在同一故障模式下某类特征属于不同故障的隶属度反映了属于某种故障的程度，若两个传感器相互支持，则隶属度间的差异必然很小。因此，可用隶属度间偏差大小来衡量各传感器相互支持的程度。引入欧氏距离来定义两个传感器的距离:

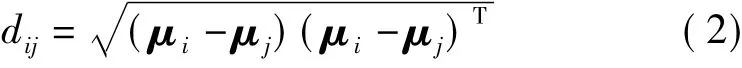
式中，μi，μj为隶属度矩阵第i行和第j行所组成的行向量，为第i个传感器和第j个传感器的某一特征属于各故障的隶属度组成的向量，代入后得:

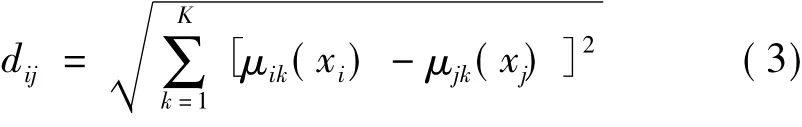
式中，μik(xi)为传感器i的某类特征值属于故障k的隶属度，μjk(xj)为传感器j的某类特征值属于故障k的隶属度，dij为置信距离测度，表征传感器之间在此特征上的差异性，0≤dij≤1。dij越大第i个传感器被第j个传感器的支持度就越低，越小支持度就越高。定义两个传感器的融合度函数:

这样，传感器i被传感器j支持的程度的大小就可用相融度函数的大小表示，则多个传感器的间就可以构成相融度矩阵:

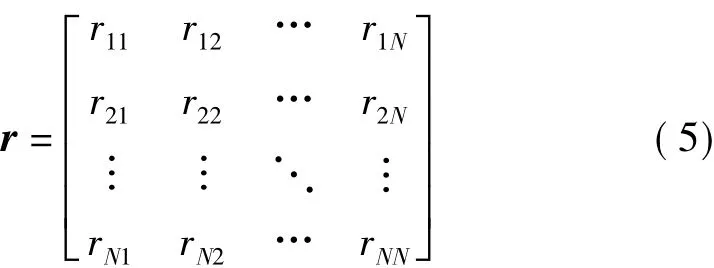
令 s=［s1，s2，…，sN］T为传感器被其它所有传感器认可的融合度向量，为了保证最大的可信度，确定第i个传感器与其它传感器的相融度时，可取其它传感器与第i个传感器相融度中的最小者，即:

式中，si为第i个传感器被其它所有传感器相融的程度。将式(4)、(5)代入后得:

1.2 不同传感器间的信息融合

在不同传感器相同特征的融合过程中，为体现不同传感器在融合中的所占比重不同，设权系数向量为:

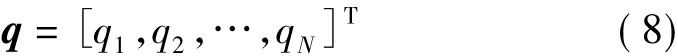
式(7)中si大表明第i个传感器被其它传感器的认可度就高，在融合的过程中此传感器所占的权重就应该大，反之就应该小，故可设第i个传感器的权系数可由si在总相融度中所占的比重确定，即:

这样，不同传感器融合后的隶属度向量

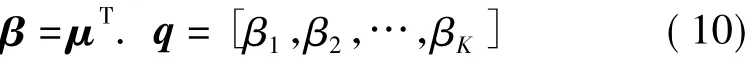
式中βK为融合后这一特征属于第K类故障的隶属度，其值为:

通过上述方法，就完成了不同传感器的某一特征的融合。用同样的方法，可进行其它特征的融合，从而得到不同传感器的其它特征的融合结果。

2 不同特征间的信息融合

2.1 证据理论

证据理论是建立在一个非空集合Θ上的理论，该集合被称为识别框架。它由一些互斥且穷举的元素组成，包含当前要识别的全体对象，记为 Θ ={θ1，θ2，θ3，…，θn］。对于Θ的每个子集 A，都属于幂集2Θ，可以指派一个值，称为基本信任分配。

定义:基本信任分配函数(BPAF)m是一个从集合2Θ到［0，1］的映射，A表示识别框架Θ的任意子集，记作 AΘ，且满足 m()=0，m(A)=1，则m(A)称为事件A的基本信任分配函数。

基本信任分配函数表示证据对证据支持事件A发生的程度，但不支持任何A的真子集;如果m(A)＞0，则称A为证据的焦元，所有焦元的集合称为核。

设BEL1和BEL2是同一识别框架U上的两个信任函数，m1和m2分别是其对应的基本信任分配函数，焦元 分 别 为 A1，…，Ak和 B1，…，Br，设 L =则证据融合后的BPAF为:

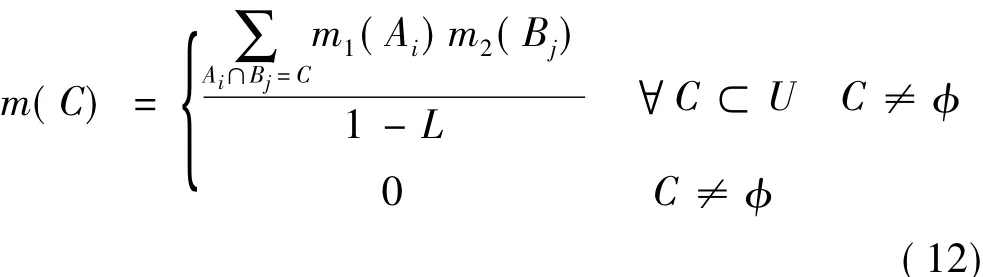
式中，L是冲突因子，反映了证据的冲突程度，1/(L－1)称为归一化因子，其作用是避免在合成时将非零信任赋给空集。该组合规则相当于在组合中将空集(冲突)等比例分配给各个集合。对于多个证据的组合，可采用此组合规则对证据进行两两融合。

2.2 利用证据理论识别故障类型

对于高速列车而言，由于提取了M类特征，所以对应的基本信任分配函数为 m1，m2，…，mM，每类特征都对应相同的K类故障，因此，基本信任分配函数的焦元也是一样的，设为 A1，…，Ak。则冲突因子 L可化为L= ∑i≠jm1(Ai)m2(Aj)＜1，则证据融合后的BPAF为:

基本信任分配函数的值可由融合后的隶属度值转化得到，为满足∑m(Ai)=1，可由以下公式来确定

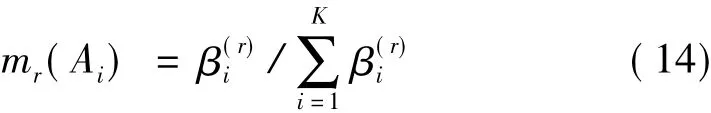
其中，mr(Ai)为r类特征属于故障类型i的基本信任分配函数，r=1，2，…，M，i=1，2，…，K。β(ir)为r类特征属于故障类型i的隶属度值，由第一节所述方法得到。由于有多类特征，可采用此组合规则对特征进行两两融合，得到最终属于各故障类型的信任分配函数m(Ai)，如m(Ak)=max m(Ai)，则判断故障类型为第k类。

3 特征类型及隶属度函数的确定

高速列车的运行速度范围很广，为了验证不同速度下本文所提出方法的有效性，以某型号动车车体在加某种实际轨道激励情况下的垂向加速度信号在40 km/h，80 km/h，120 km/h，140 km/h，160 km/h，200 km/h，220 km/h的实验数据来进行处理。故障分为列车走行部正常、空簧失气、抗蛇形全拆、横向减震器全拆四种故障(分别用故障1－故障4表示)。基于车体的自震频率、幅值非线性误差、横向响应、稳定性及幅频特性和相频特性等方面的考虑，传感器型号选择LC0709－2，其性能指标为:量程±2 g;－3 db频率响应为500 Hz;灵敏度1 000 mV/g;非线性误差0.2%;噪声密度 0 .19 mg/横向响应＜5%。以传感器1(车体前枕梁上地板)，传感器2(车体中地板)，传感器3(车体后枕梁上地板)，传感器4(后中心销上地板)的四个传感器测得的垂向加速度数据为例(垂向振动主要与线路水平度和车辆走行部及减振器的状态有关)，采样频率为243 Hz，不同速度下每个传感器每种故障样本数为140，数据段长度1 024，其中的1/2样本，也就是70个样本用于得到模糊隶属度函数的参数，其余的70个样本用于识别。

3.1 特征类型的选取

信息熵是对系统混乱程度的描述，系统越混乱熵就越高，对于对高速列车走行部不同的故障，振动能量状态的变化的有序程度是不一样的，因此本文采用信息熵对高速列车的不同故障进行描述。不同的熵可以从不同方面的有序程度进行描述。系统信息熵的定义为［14］:设W是一个可测集合类v生成的σ代数和具有p测度，p(W)=1的勒贝格空间，且W可表示为其有限划分C={Ci］中互不相容集合的形式，即:

则对于该划分C的信息熵为:

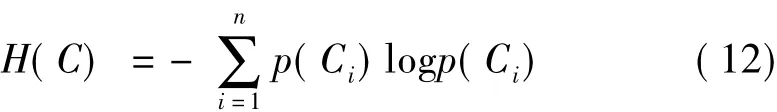
其中，μ(Ai)为集合 Ai的测度，i=1，2，…，n。

本文采用小波能量谱熵、功率谱熵、奇异谱熵、小波空间状态特征谱熵四种熵特征［14］来对高速列车的故障情况进行描述。

3.2 隶属度函数类型的确定

传感器的测量值可以看作是目标属性的真实值与噪声信号的叠加，假设测量噪声为均值为零的高斯白噪声，则各种故障情况的同一熵特征也服从高斯分布，因此，隶属度函数可选择高斯型，即

其中，a，b分别是期望和均方差，用140组样本中的70组通过参数估计的方法得到，这样，就可以得到式(1)的隶属度函数矩阵。

为了比较不同熵相同位置及相同熵不同位置对于不同故障的差异，以下各表列出了在140 km/h时各熵特征不同位置传感器下不同故障的a，b值。从表中可以看出，小波能量谱熵、功率谱熵、奇异谱熵、小波空间状态特征谱熵能有效的描述不同位置不同类型的故障。由于篇幅原因在其它速度下不再一一列出。

表1 小波能量谱熵在不同情况下的期望和均方差Tab.1 Expectation and variance of wavelet energy spectrum entropy

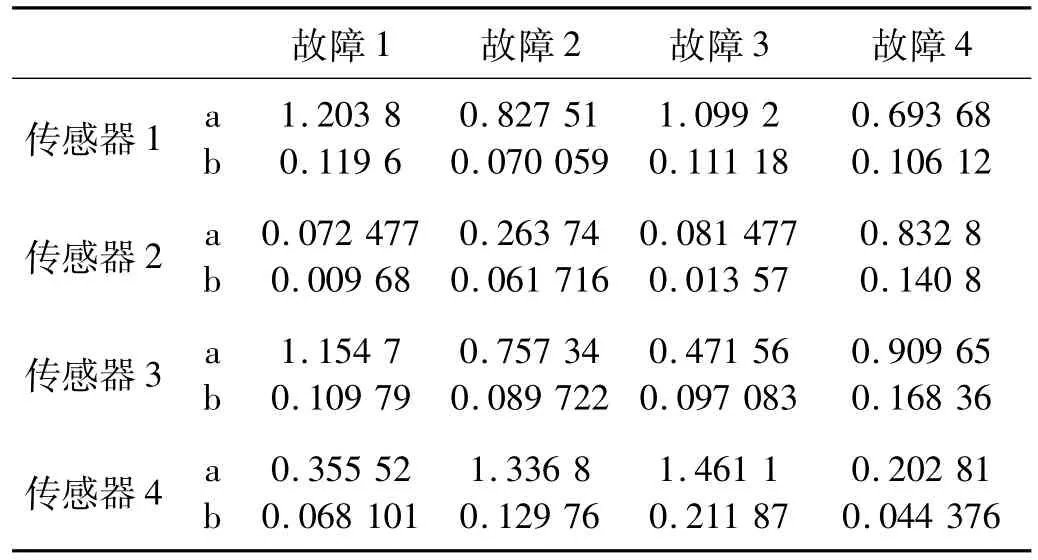
表2 功率谱熵在不同情况下的期望和均方差Tab.2 Expectation and variance of power spectrum entropy

表3 奇异谱熵在不同情况下的期望和均方差Tab.3 Expectation and variance of singular spectrum entropy

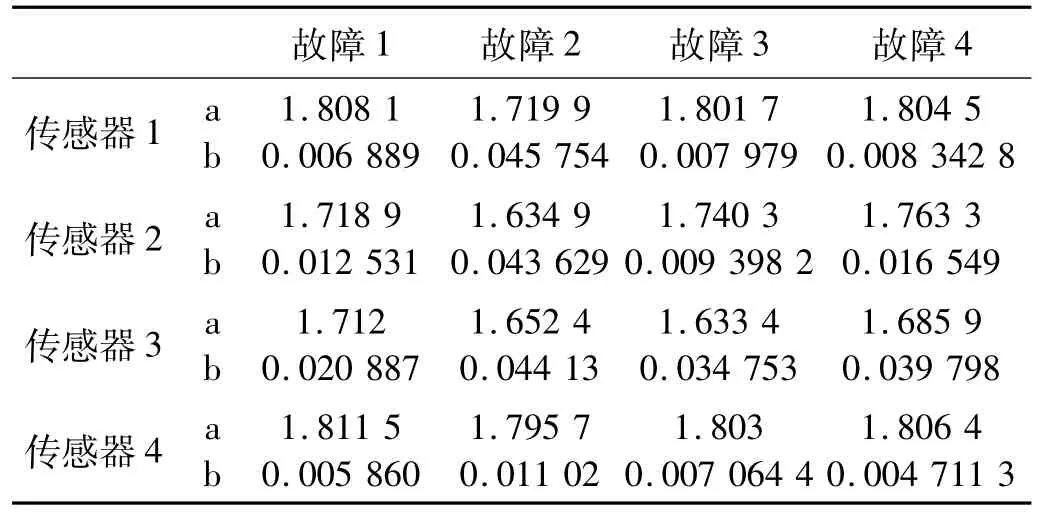
表4 小波空间状态特征熵在不同情况下的期望和均方差Tab.4 Expectation and variance of wavelet space state feature spectrum entropy

4 故障类型的识别

对4个传感器测得的4种故障的样本数据提取4种熵特征、确定出隶属度函数的参数后，在不同速度下对剩下的样本数据用1、2小节介绍的方法分别进行同一特征不同传感器的数据融合和不同特征的数据融合。例如，在故障3(抗蛇形减震器全拆)条件的提取4个传感器数据的某一样本小波能量谱值(特征1)分别为 x1=0.826 75，x2=0.429 87，x3=0.268 09，x4=0.861 47代入(1)式可得到属于各故障模式的隶属度值:

由式(4)得相融度矩阵:

由式(6)得:

权重系数向量为:

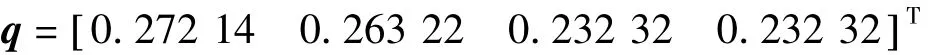
融合后的属于各故障的隶属度为:

由式(14)得到转换后的基本信任分配函数值:

用同样的方法，可得到其它特征的基本信任分配函数值:

然后，用式(13)的方法对 m1、m2、m3、m4两两融合得到:

m=[0.014 31 0.000 39 0.969 8 0.015 5]

由此判断，故障类型为故障3(抗蛇形减震器全拆)，与实际情况相符。对于其它样本数据也可采用同样的方法进行识别，最后由正确识别的次数除以总的次数就可以得到各种情况的识别率。

为比较单传感器和多传感器识别的优劣，分别列出单传感器和多传感器在不同速度下的识别率，如图2和图3。

图2 单一传感器的识别率Fig.2 Recognition rate of single sensor

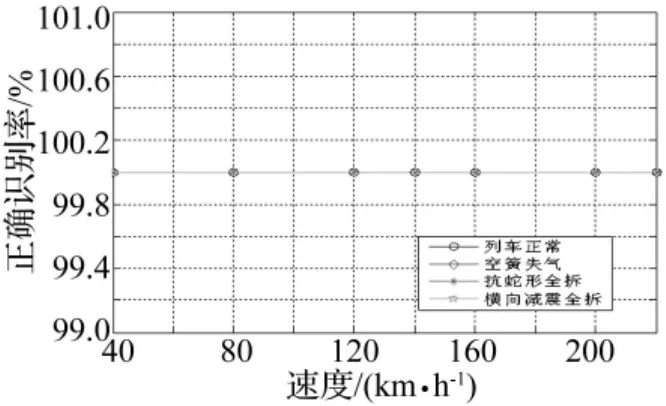
图3 四个传感器融合后的识别率Fig.3 Recognition rate of four sensors

由图2可以看出，对于单个传感器而言，传感器2(车体中地板)的识别率较好，最低都达到了82%以上，其中对抗蛇形减震器全拆故障的识别达到了100%;其它传感器的识别率对于不同故障起伏较大，最低的识别率只有45%，四个传感器来说，在120 km/h条件下相对于其它速度识别率较高。但是，总体上来说，不同传感器不同速度下各故障的识别率相差较大，单个传感器的识别率都不够理想。由图3可知，经四个传感器融合后的识别率得到了大幅的提升，每一种情况的各种故障识别率都达到100%，说明本文的方法对高速列车走行部故障的识别是有效的。

5 结论

利用多传感器的信息和数据的多类特征识别高速列车走行部的故障，可以避免单一特征、单一传感器的局限性，综合考虑各传感器的多个特征的情况，可以减小传感器不确定性误差带来的影响。本文提出的基于模糊证据理论的多特征、多源信息融合的走行部故障识别方法，综合考虑了不同的传感器信息的各类特征间的相互关系，避免了融合过程中的主观化，能对不同传感器测量的各种情况的故障数据的各特征进行有效的融合，实验表明了该方法的有效性。

［1］陈特放，黄采伦，樊晓平.基于小波分析的机车走行部故障诊断方法［J］.中国铁道科学，2005，26(4):89－92.CHEN Te-fang，HUANG Cai-lun，FAN Xiao-ping.Fault diagnosis method for locomotive bogies based on wavelet analysis［J］.China Railway Science，2005，26(4):89－92.

［2］黄采伦，樊晓平，陈春阳，等.基于小波系数提取及离散余弦包络分析的机车牵引齿轮故障诊断方法［J］.铁道学报，2008，30(2):98－102.HUANG Cai-lun，FAN Xiao-ping，CHEN Chun-yang，et al.Fault diagnosis method of locomotive driven gear based on envelopment analysis of wavelet coefficients extraction and DCT［J］.Journal of the China Railway Society，2008，30(2):98－102.

［3］丁夏完，刘葆，刘金朝，等.基于自适应STFT的货车滚动轴承故障诊断［J］.中国铁道科学，2005，25(6):24－27.DING Xia-wan， LIU Bao， LIU Jin-zhao， et al. Fault diagnosis of freight car rolling element bearings with adaptive short-time fourier transform ［J］.China Railway Science，2005，25(6):24－27.

［4］Chen L，Zi Y Y，Cheng W，et al.EEMD －1.5 dimension spectrum applied to locomotive gear fault diagnosis［J］.Proc.of International Conference on Measuring Technology and Mechatronics Automation，2009，1:622－625.

［5］ Lei Y G，He Z J，Zi Y Y.Application of a novel hybrid intelligent method to compound fault diagnosis of locomotive roller bearings［J］.Journal of Vibration and Acoustics，Transactions of the ASME，2008，130(3):034501.

［6］Lei Y G，He Z J，Zi Y Y.EEMD method and WNN for fault diagnosis of locomotive roller bearings［J］.Expert Systems with Applications，2011，38(6):7334 －7341.

［7］Szymannski G M，Czechyra B.Identification of failures of an internal combustion engine for locomotive in the base of an amplitude spectrum from a vibrational signal［J］.Scientific Papers of the Institute of Machine Design and Operation of the Technical University of Wroclaw，2002，86(26 II):299－305.

［8］林云，李一兵，Zhou R L.灰色关联和证据理论在故障识别中的应用和改进［J］.应用基础与工程科学学报，2011，19(2):314－322.LIN Yun， LI Yi-bing，Zhou R L. Application and improvement of gray correlationand evidence theory in fault recognition［J］.Journal of Basic Science and Engineering，2011，19(2):314－322.

［9］ Jousselme A L， Liu Chun-sheng， Grenier D， et al.Measuring ambiguity in the evidence theory［J］.IEEE Transactions on Systems，Man，and Cybernetics-TSME，Part A，2006，36(5):890 －903.

［10］韩峰，杨万海，袁晓光.基于模糊集合的证据理论信息融合方法［J］.控制与决策，2010，25(3):449－452.HAN Feng，YANG Wan-hai，YUAN Xiao-guang.Evidence theory information fusion method based on fuzzy set［J］.Control and Decision，2010，25(3):449 －452.

［11］徐琰珂，梁晓庚，贾晓洪.利用模糊证据理论的信息融合方法及其应用［J］.哈尔滨工业大学学报，2012，44(3):107－111.XU Yan-ke，LIANG Xiao-geng，JIA Xiao-hong.Information fusion based on fuzzy evidence theory and its application in target recognition［J］. Journal of Harbin Institute of Technology，2012，44(3):107 －111.

［12］ XU Xiao-bin，WEN Cheng-lin，LI Zhi-liang.A new method for constructing fuzzy evidence based on the non-consonant random set［J］.Journal of electronics，2009，26(1):31－37.

［13］耿俊豹，黄树红，金家善，等.基于信息熵贴近度和证据理论的旋转机械故障诊断方法［J］.机械科学与技术，2006，25(6):663－666.GENG Jun-bao，HUANG Shu-hong，JIN Jia-shan，et al.Rotating machine fault diagnosis method based on information entropy and evidence theory［J］.Mechanical Science and Technology，2006，25(6):663 －666.

［14］耿俊豹，黄树红，陈非，等.基于信息熵贴近度的旋转机械故障诊断［J］.华中科技大学学报(自然科学报)，2006，34(11):93－95.GENG Jun-bao， HUANG Shu-hong， CHEN Fei，et al.Rotating machinery fault diagnose is based on close degree to inform at ionentropy［J］ .J.Huazhong Univ.of Sci.＆Tech.(Nature Science Edition)，2006，34(11):93 －95.