汽车天窗风振噪声分析与优化控制
2014-09-18杨振东谷正气董光平杨晓涛申红丽
杨振东,谷正气,董光平,杨晓涛,申红丽
(1.湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082;2.湖南涉外经济学院 机械工程学院,长沙 410205;3.湖南工业大学,湖南 株洲 412007)
汽车行驶时,开启天窗会引发风振噪声,这种频率在20 Hz左右,强度高达到100 dB以上,产生的脉动压力使驾驶员感到烦躁和疲倦,严重影响了驾驶员和乘员的舒适性。在汽车设计阶段,必须考虑风振噪声的影响。因此,研究天窗风振噪声的产生机理及控制方法有很重要的实际意义[1]。
国外对风振噪声的研究起步很早。但早期的研究方法主要依赖于风洞试验或者实车道路试验,并取得了一系列的成果[2-4]。他们的研究表明风振噪声一定的速度范围内存在相当明显的峰值,是由车窗开口处的边缘噪声激起车内空间亥姆霍兹共振效应引起的,并提出改变车辆内部声腔的固有频率,来避免这种声共振。Ota等[5]对二维天窗全开状态下的汽车风振噪声进行了仿真研究,确定了引起乘员室共振的临界速度并研究了天窗导流板安装角度对风振噪声的影响。最后制作了一个矩形空腔进行了实验对比。该工作显示了仿真方法在汽车风振噪声研究方面的巨大应用潜力。Karbon等[6]采用更为复杂的三维汽车模型来计算天窗风振噪声,并提出了两种有效的方法来降低噪声,即安装导流片及合理设置天窗玻璃的开启程度,结果显示这两种方法都起到了良好的效果。An等[7]对汽车天窗风振噪声的机理进行了探索,并仔细研究了天窗导流板的参数(导流板高度、安装角度)及天窗玻璃开启程度对风振噪声的影响,这些工作为天窗风振噪声的控制提供了重要的参考。
肖朕毅等[8]首次将国外汽车风振噪声方面的研究情况做了较为系统地介绍,为国内学者研究汽车风振噪声提供了参考。汪怡平等[9]对汽车天窗的风振噪声问题做了研究,在对汽车外部瞬态流场进行数值模拟的基础上,获得了天窗风振噪声的频率以及驾驶员耳旁的相应声压级,提出了安装导流板及合理开启天窗等两种有效控制措施。黄磊[10]介绍了安装网状挡风条和减小天窗玻璃开口面积两种天窗风振噪声的控制方法,重点探讨了网状挡风条的降噪原理,最终的试件在风洞实验中取得了良好的降噪效果。康宁等[11]对有天窗的简化Golf 1.6轿车进行仿真,随着天窗后移及加宽,得出了监测点处的声压级逐渐减小的结论,并得到了较合理的天窗尺寸及安装位置。胡亚涛等[12]以实车模型的1∶5简化模型进行了空腔绕流的数值计算,并利用低速静音风洞进行了实验,研究结果表明除了特征频率下的风振噪声,还存在着较大范围的宽频气动噪声,并且这种宽频噪声会随着流速的增大而显著增加。
增加或改进天窗空气动力学附加装置可以很好地降低天窗风振噪声,较大地改善汽车乘坐舒适性。对天窗导流板而言,如何将其安装角度和造型结合进行优化到目前还没有看到。本文以某轿车为研究对象,通过对一个涡脱落周期内涡运动的分析,从而揭示了天窗风振噪声产生的机理。并以车内乘员耳旁的加权噪声值为优化目标,以天窗导流板的形状参数和安装角度为设计变量,并对设计变量进行了敏感度分析,评估了设计变量对优化目标的影响。此后,通过试验设计(DOE)选取的样本点,由仿真计算得到相应响应值,在此基础上构建了Kriging近似模型,并评估了Kriging近似模型替代数值模拟的可行性及精确性。最后,采用遗传算法对构建的近似模型进行优化设计,得到了最优的设计变量和优化目标。
1 参照车型天窗风振噪声道路试验
本文所开展的研究是在汽车设计阶段进行仿真和分析,参照车型为已经上市几年的某知名豪华轿车,在仿真分析之前对参照车型由于天窗开启引起的风振噪声进行了实车道路试验。试验是在A级路面上进行,天气晴好,环境温度为24℃,环境噪声小于40 dB,仅2人乘坐于前排,副驾驶员负责数据的采集。采用LMS公司噪声测试设备,试验分析软件Test.Lab 8B,数据采集系统为16通道LMSSCADAS,使用丹麦GRAS公司的前置放大器和麦克风,测试车速最低为20 km/h,最高车速为160 km/h,间隔5 km。每一车速采样5次,取风振噪声峰值的平均值。监测点位于驾驶员右耳,天窗开启风振噪声峰值随车速变化测试结果如图1所示。
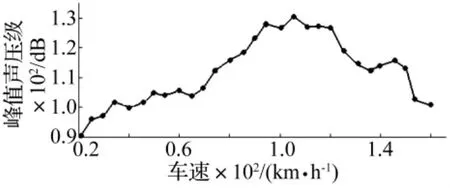
图1 不同车速下的天窗风振噪声峰值Fig.1 Evolution of sound pressure level as a function of the vehicle speed during sunroof buffeting
从图1中可以看出,在天窗完全开启的条件下,随着车速的提高,风振噪声的峰值增加,在车速为20 km/h时,驾驶员右耳风振噪声峰值就已经超过90 dB;在105 km/h左右达到最大,达到132 dB,风振频率对应为23 Hz。对参照车型所进行的天窗开启风振噪声道路试验,为对目标车型进行数值仿真分析提供了依据。
2 大涡模拟理论以及FW-H方程
2.1 大涡模拟的控制方程
将Navier-Stokes方程在物理空间进行过滤,得到流体LES控制方程
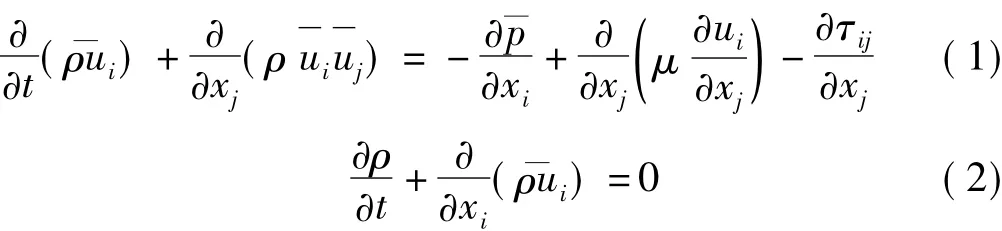
式中ρ为流体密度;xi、xj为坐标轴分量,ui和uj为过滤后的速度分量;μ为湍流粘性系数;τij为亚格子尺度应力。
为使控制方程封闭,当前,采用较多的亚格子模型是涡旋黏性模型
式中δij为克罗内克系数;νt为亚格子湍流黏性系数;sij是求解尺度下的应力变化张量分量。
2.2 FW-H方程
FW-H方程由 Ffowcs Williams等[13]利用 Lighthill的声学近似理论推导出了适合流体中运动固体边界条件的FW-H方程:
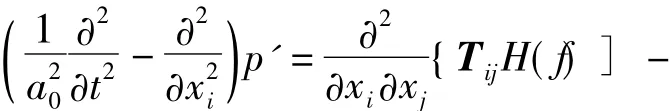
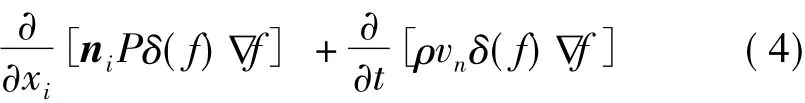
式中p'为声压,ni为表面法向量,vn为法向速度,a0为声速,Tij为Lighthill张量。方程右侧三项分别代表四极子、偶极子和单极子。由式(4)可以求出自由空间的声压。文中未考虑壁面的散射、反射和折射,只计算了声源及其自由场中的辐射。
图2 模型示意图Fig.2 Car body model
3 计算模型及计算方法
3.1 计算域及网格划分
以某安装内藏式天窗的轿车为研究对象,天窗尺寸为320 mm ×720 mm,为提高效率,将研究的重点集中到天窗风振噪声上,在不对研究结果构成影响的前提下,本文对整车模型远离天窗的部件做了适当简化,最后得到的整车简化模型如图2所示。

图3 车身纵对称面上的网格分布Fig.3 The mesh distribution of the longitudinal cross section of symmetry
计算域为包围汽车模型(长L,宽 W,高 H)的长方体长11 L,宽 5 W,高约 4 H。图3为车身纵对称面网格分布图,车身处使用密度盒进行局部加密,生成局部精细的网格。由于四面体网格的贴体性较好,本文采用四面体网格。最小的面网格尺寸是2 mm,最大的面网格尺寸是32 mm。边界层是速度梯度很大的薄层,为了模拟边界层效应,在车身表面,生成了三层精细的棱柱网格。第一层网格高度为1 mm,增长比例设定为1.2,如图4所示。越靠近车身表面网格越密,并对参数变化梯度大的区域进行局部加密,为捕捉天窗附近气流的运动细节,对天窗附近区域也进行了局部加密,如图5所示。最终的网格数量约为820万左右。

图4 边界层网格Fig.4 A finer grid scheme in boundary layer
3.2 边界条件
参考道路试验数据,选择风速为30 m/s。本文计算所用的边界条件如表1:

图5 天窗附近网格Fig.5 Grids around sunroof

表1 边界条件Tab.1 Boundary conditions
3.3 计算方法
对于瞬态问题,一般先进行稳态仿真,然后将稳态结果作为瞬态的初始条件。稳态数值模拟求解采用Realizable k-ε湍流模型,压力速度耦合采用SIMPLE算法,差分均采用二阶迎风格式。
待稳态计算结果收敛后,作为瞬态求解的初始值。采用大涡模拟(LES)进行瞬态求解,监测点选择在驾驶员的右耳旁和乘员的左耳旁,采样时间设为2 s,由于流场从开始计算到稳定需要一个过程,因此只记录1-2 s的时域信号;时间步长决定了计算的最高频率,风振噪声主要集中在低频[14],所以本次计算的最高频率设定在250 Hz,为了便于观察,图形最高频率只显示到200 Hz,时间步长为0.002 s,因此总步数为1 000步,每时间步迭代20次。
4 天窗风振噪声机理及抑制措施
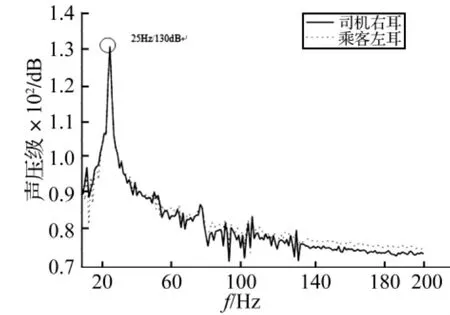
图6 监测点声压频谱图Fig.6 Sound pressure level at monitor points
4.1 天窗风振噪声形成机理
图6 为天窗全开时监测点的声压频谱图,由图6可知,该车在天窗全开时于25 Hz左右存在明显的共振,且峰值达到了130 dB,并且两监测点的频谱曲线非常相似。将图6和图1对比可以看出,在监测点驾驶员右耳处,就风振噪声峰值而言,目标车型仿真值与参照车型实验值相差3 dB,频率相差2 Hz。考虑到参照车型和仿真车型有一定的差别,能够说明仿真结果比较可靠。
由图7流体质点运动的轨迹可以看出,漩涡在天窗前沿开始形成并产生脱落,与压力较低的部位十分吻合。为更好的观察涡的形成与脱落,可以采用制作动画的形式,通过显示流体变量如静压在一段时间内的变化来揭示天窗处流场的非稳态特性,解释天窗风振噪声产生的机理。

图7 天窗纵截面压力和速度流线(t=2.970 s)Fig.7 Contours of instantaneous pressure(Pa)and velocity streamline at t=2.970 s
由共振频率f=25 Hz可知天窗处涡的脱落周期为T=0.04 s。图 8 中(a) ~(h)分别为 t=0、T/8、T/4、3T/8、T/2、5T/8、3T/4、7T/8、T 的压力云图。
在t=0时刻,天窗开口的中间位置开始产生一个中心压力较低的漩涡,且车内压力相对较高。在t=T/8时刻,漩涡继续往下游运动并逐渐变大,同时车内压力逐渐升高。在t=T/4时刻,漩涡在继续向下运动的同时漩涡中心压力逐渐降低,同时车内压力几乎达到最高。在t=3T/8时刻,漩涡开始撞击天窗的后缘,同时负压开始向车内扩展。在t=T/2时刻,漩涡脱落并侵入乘员室内部,同时负压范围开始向天窗开口前缘扩展。在t=5T/8时刻,漩涡继续向车内运动,同时负压范围扩展至天窗开口前缘,乘员室内压力持续降低。在t=3T/4时刻,漩涡继续向车内流动,同时扩展至天窗开口前缘的负压开始诱导第二个漩涡产生,此时车内全为负压,压力几乎降到最低。在t=7T/8时刻,第一个漩涡即将耗散完,而第二个漩涡已初具雏形,同时车外正压从天窗开口后缘开始向车内扩展。在t=T时,一个周期结束,流场回到t=0时刻的状态,下一个周期开始形成。
4.2 天窗风振噪声抑制措施
降低天窗风振噪声的主要措施分为主动控制与被动控制。被动控制措施主要有:① 天窗开口前缘安装导流板。导流板可导走由开口前缘剪切层产生的涡流,从而减轻涡流脱落后对开口后缘的撞击。② 合理设置天窗玻璃开启程度。这样做同样是为了避免涡流撞击开口后缘。③ 改变天窗后缘与水平面间的夹角。④天窗中间设置中立柱。主动控制则是利用声波的干涉相抵消原理,通过在声场中设置同频反相振动装置(如电控扩音器等)来降低噪声。
由于人们安装天窗就是为了充分享受由此带来的各种好处,所以合理设置天窗玻璃开启程度及天窗中间设置中立柱并不能不让人满意。改变天窗后缘与水平面间的夹角会破坏整车造型,往往也不可行。而主动控制需要安装的机构复杂,不仅成本高,具体实施起来也比较困难,故在实际应用中还很不成熟。综上所述,本文将研究重点集中于天窗导流板的优化上。文献[15]提及了两种形状的导流板,一种边缘是平直的(导流板a),另一种上面开了数个凹槽 (导流板b),其实验证明在50 km/h时导流板a降低了5 dB峰值噪声,导流板b降低了7 dB峰值噪声,导流板模型如图9所示。

图8 天窗开启瞬态压力云图(Pa)Fig.8 Contours of instantaneous pressure at eight time instants for one period(Pa)

图9 两种导流板示意图[15]Fig.9 Two kinds of deflectors[15]
在下文的优化设计环节中,本文选择开槽型导流板为研究对象。
5 开槽导流板优化设计
5.1 设计变量的选取
本文选取某轿车的天窗开槽导流板作为优化对象,其几何模型如图10所示。根据天窗导流板的形状及安装特征,导流板宽度保持为50 mm,选取参数导流板安装角度angle(°)、开槽宽带width(mm)、开槽深度depth(mm)来描述导流板。分别简称为A、W、D。
5.2 目标函数与约束函数
由于在汽车行驶过程中,汽车由驾驶员实际操控,如果开启天窗引起的噪声值过高,根据文献[16],可知噪声过高会造成驾驶员注意集中力下降,这样易造成交通事故,所以在综合考虑时,降低驾驶员耳旁的噪声值应处于相对较重要的地位。因此,以汽车匀速行驶下开启天窗的驾驶员右耳及副驾驶乘员左耳的噪声加权值作为本文优化目标,在优化时配以不同的权重,优化问题可描述如下:

式中Pd、Pp分别为驾驶员右耳及副驾驶乘员左耳处的噪声值,ω1、ω2为权重系数,分别取为 0.6、0.4,其中 A=50°、W=40 mm、D=20 mm 时初始监测值 P0=116.3 dB此处P≤116.3 dB是要求最终的优化结果不能增大初始噪声值,A、W和D的取值范围是根据导流板的实际情况衡量选取的,并且所有取值均为整数。
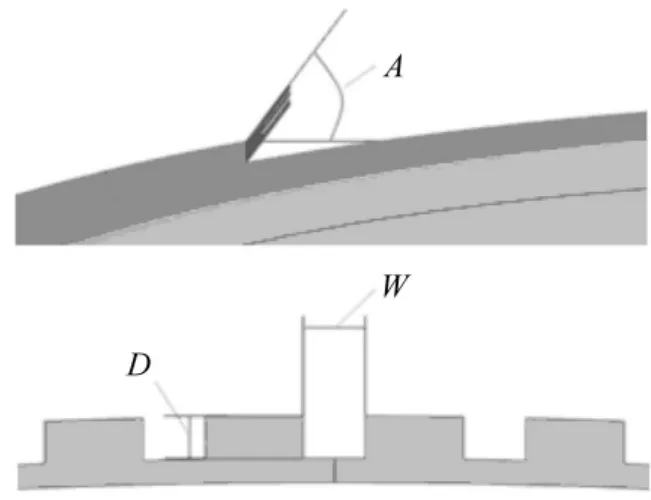
图10 天窗导流板参数Fig.10 Parameters of deflector
5.3 试验设计
常用的试验设计方法有中心组合试验设计、全因子试验设计、正交试验设计、均匀试验设计与拉丁超立方试验设计等。拉丁超立方试验设计的本质在于控制抽样点的位置,避免抽样点在小领域内重合的问题。利用这种方法构造的近似模型整体性好[17]。因此针对较大型空间的采样,工程中常采用拉丁方试验设计,故本文选取此方法作为试验设计方法。
根据设计变量的取值范围,选取的优化设计变量共3个,采用拉丁超立方抽样方法选取了20组样本点进行CFD模拟计算,得到20组响应值,设计的具体方案如表2所示。
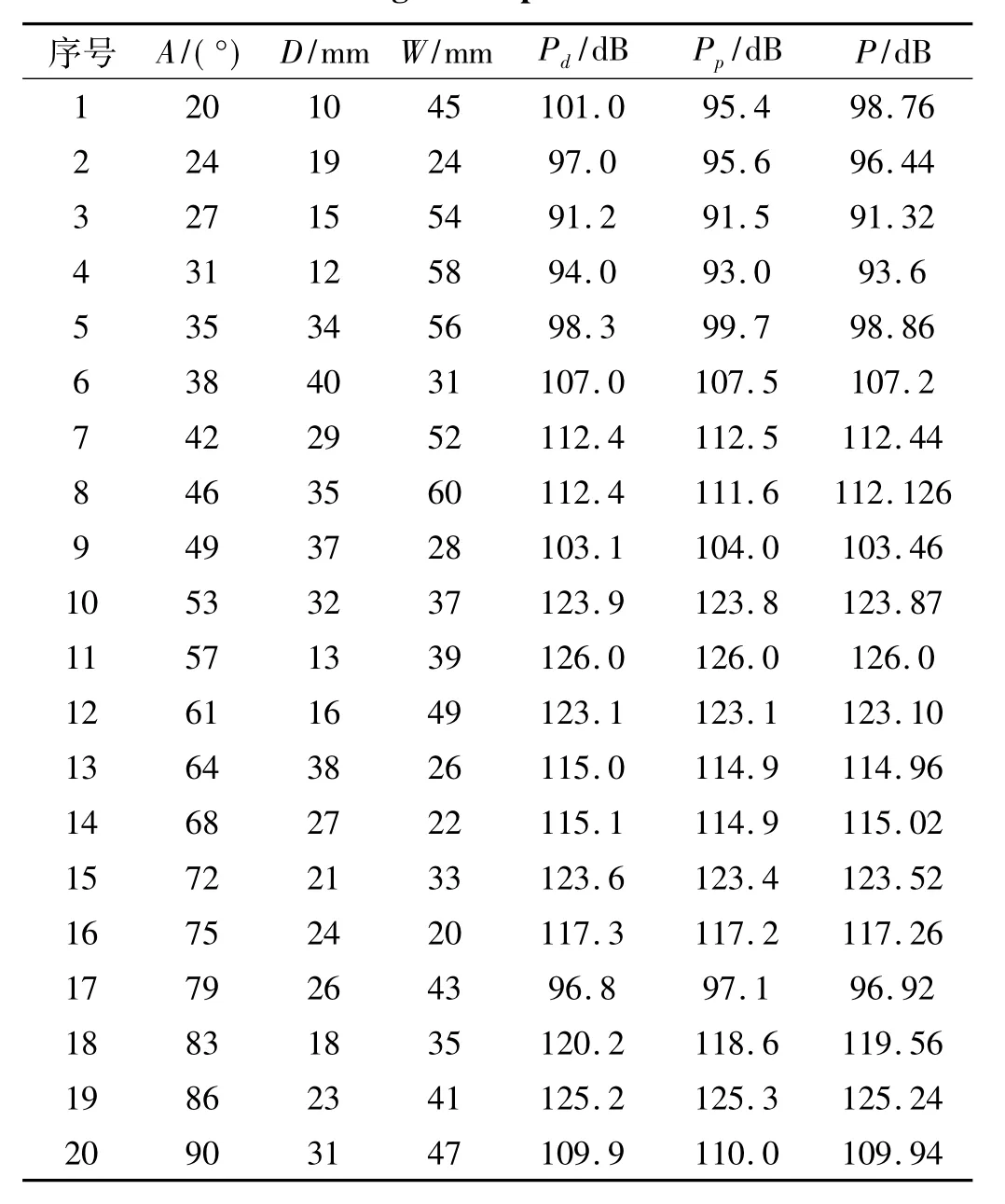
表2 试验设计方案Tab.2 Design of Experiment scheme
根据提供的优化拉丁方试验设计的方案对表2进行分析,得出设计变量与优化目标间的相应关系。图11分别为设计变量A、D及W对车内噪声值P的主效应图。从图11中不同曲线的斜率可以看出,对车内噪声值P影响最大的设计变量是A,D的影响次之,W影响最小。同时由图11还可看出:相对于A,车内噪声值P随着A的增大而增大;相对于D,车内噪声值P随着D的增大先较迅速地减小然后缓慢增大;而相对于W,车内噪声值P基本上随着W的增大而减小。
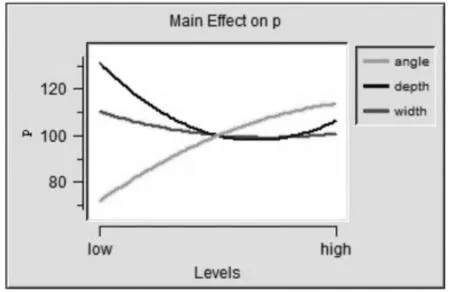
图11 设计变量主效应图Fig.11 Main effect of design variables
图12 为设计变量A、D及W对车内噪声值P的交互效应。D与W之间的交互效应较为明显;而A和D、A和W之间的交互效应则不是很明显,曲线之间不存在交叉。

图12 设计变量交互效应图Fig.12 Interaction effect of design variables
图13 为车内噪声值的Pareto图。对车内噪声值P影响最大的设计变量依次是A、D和W。D与W之间的交互效应最为明显,A和D次之,A和W最小。W对车内噪声值的影响虽然不是非常显著,但是它与A和D之间的交互效应对车内噪声值的影响却是不能忽视的。

图13 车内噪声值的Pareto图Fig.13 Pareto plot for P
由以上主效应、交互效应及Pareto图的分析可得出如下结论:不仅单个设计变量的变化会对优化目标产生影响,同时,设计变量之间的交互效应也会对优化目标产生显著的影响。
5.4 近似模型的建立
Kriging模型最早由 Krige[18]提出,是一种估计方差最小的无偏估计模型,它由全局模型与局部偏差迭加而成,数学表达式如式3所示:

式中:f(x)是类似于响应面模型的多项式表达式的近似模型;z(x)是均值为0、方差为σ2、协方差非零的随机过程;y(x)是未知的近似模型。f(x)起设计空间中的全局近似作用,z(x)在全局模型的基础上创建了局部偏差[19]。与其他模型相比,Kriging模型构建的近似面可以覆盖所有的样本点,近似面质量很高,因此在本文中采用Kriging模型用于构建近似面。
将得出的设计变量与优化目标之间的响应关系采用Kriging方法建立了设计变量与优化目标之间的近似模型。
为检验所建立的近似模型的拟合精度,在设计空间中选取20组试验设计方案外的任意3个实验点进行CFD仿真计算,并与近似模型得出的计算结果进行对比,对比结果如表3所示(表中的相对误差为仿真结果与近似模型计算结果之差的绝对值与仿真结果之比)。

表3 近似模型拟合精度分析Tab.3 The fitting precision of the Approximate Model
从表3中可以看出,采用近似模型计算的结果与直接采用CFD仿真计算所得出的结果是很接近的,两种方法得出的车内噪声值的相对误差值为2.8%。因此通过实验设计方案建立的近似模型可以很好的反应设计变量与其响应之间的关系,且建立的近似模型其精度很高,直接用来代替CFD仿真计算是可行的。
5.5 优化结果及分析
遗传算法简称GA(Genetic Algorithms)是由Holland[20]提出的一种全局优化搜索算法,其基本思想是基于达尔文进化论和孟德尔遗传学说。它将问题表示成群体,根据适者生存的原则,从中选择出适应环境的个体进行复制,通过交叉、变异2种基本操作产生新一代更适合环境的群体,最后收敛到一个最优个体,求得问题的最优解。遗传算法被广泛地应用于工程优化设计,尤其是航空气动优化领域[21-22]。
按照优化目标的个数,遗传算法一般可以分为单目标遗传算法和多目标遗传算法两类。在传统遗传算法基础上发展而来的多岛遗传算法(Multi-island Genetic Algorithm)是单目标遗传算法的一种。这种方法通过将整个进化群体划分为若干子群体,称为“岛屿”,在每个岛屿上对子群体独立的进行传统遗传算法的选择、交叉、变异等遗传操作。多岛遗传算法定期随机选择一些个体进行“迁移”操作,将其转移到别的岛屿上,通过这种方式,可以维持群体的多样性,从而抑制了早熟现象。多岛遗传算法作为一种伪并行遗传算法可以更好的在优化域中寻找全局最优解[23]。
在本文中,优化目标为单一目标,根据建立的近似模型,采用多岛遗传算法进行寻优设计,初始种群个数为20,迭代次数为100,最终得出模型最优解。对得到的最优解进行CFD计算验证,误差均在3%以内,以驾驶员右耳声压为评价指标,具体对比结果见表4。优化导流板后监测点的噪声值比初始导流板减少了21.6%,具体数值见表5。
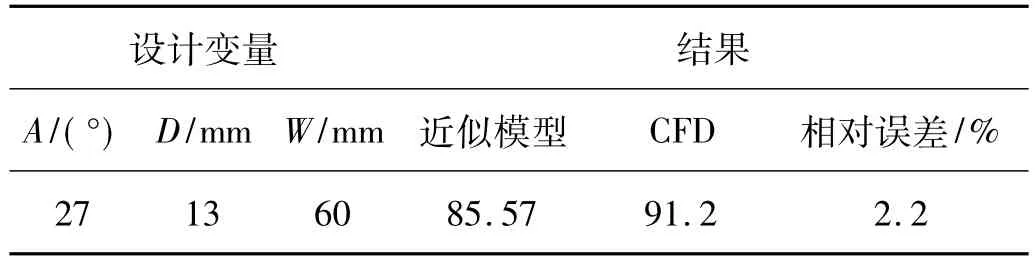
表4 最优解误差对比Tab.4 Optimal Results

表5 优化改进效果Tab.5 Comparisons between optimization deflector and original deflector
两种导流板相同监测点(驾驶员右耳)处的声压频谱如图14所示。可以看出,优化后的导流板相对于初始导流板具有明显的降低风振噪声的作用,在驾驶员右耳处峰值声压降低了25.1 dB,相比降低了21.6%。
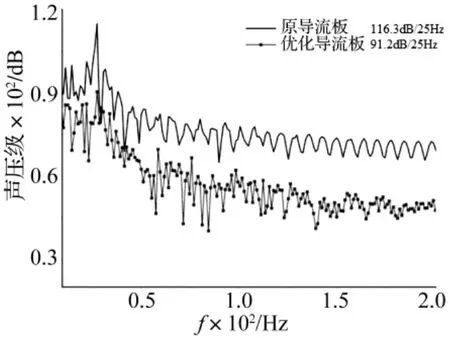
图14 在驾驶员的右耳获取两种导流板的声压频谱图对比Fig.14 SPL comparison between original deflector and optimization deflector at the driver’s right ear
Q准则是一个用来描述湍流流场(涡量和压力等)的标量。为了描述导流板对涡脱落的抑制作用,本文采用Q准则来描述湍流流场,Q是速度梯度张量的二阶不变量,可以表示成如下形式:
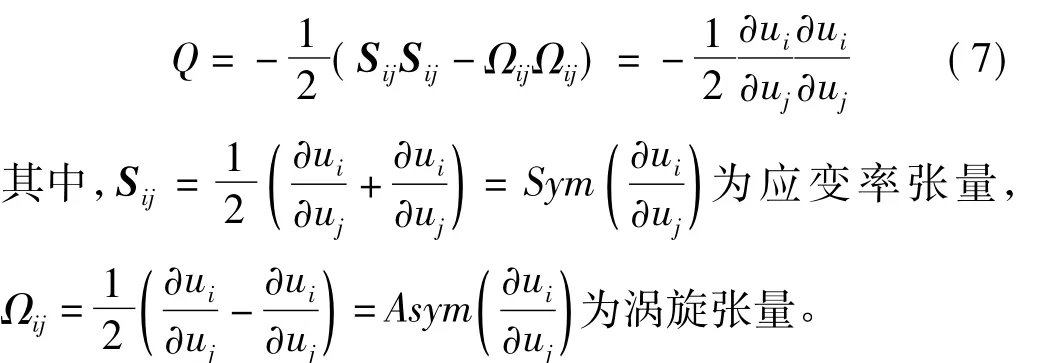

图15 无导流板和安装导流板后瞬时的Q准则面(Q=2 490)Fig.15 Iso-surfaces of Q -Criterion comparison between sunroof without deflector and with optimized deflector(Q=2 490)

图16 天窗纵截面的λ2Fig.16 λ2 contours at the sunroof center-plane
如图15为瞬时Q准则Iso-surface,从图15(a)中可以看出,由于无导流板,则不存在对天窗前沿处产生的剪切层涡流的破坏,大尺度的涡侵入,从而在乘员舱内涡旋效应较强。从图15(b)和图15(c)中可以看出,而安装了导流板后,导流板对剪切层能量起到耗散作用,破坏了周期性的涡脱落,则不存在较大的涡旋效应,以致于降低了乘员舱内的压力脉动,从而声场强度降低。
为了更好的显示不同导流板形状对风振噪声的抑制,本文进一步引入λ2尺度显示涡核来进行流场的充分对比分析[24],如图16所示,其对应的声压频谱曲线如图17所示。
从图16和图17中可以看出,由于没有导流板,涡在天窗前沿形成并向下游传输,在天窗后沿的前方生成一个较大的涡,撞击后沿并引起车内强烈的压力脉动,在监测点达到130 dB的峰值声压,其对应频率为25 Hz。天窗安装了初始导流板后相对于无导流板的天窗而言,初始导流板耗散了剪切层,导致侵入车内的涡量减少,在监测点峰值声压降到116.3 dB,其对应频率是25 Hz。优化后的导流板相对于初始导流板和无导流板而言,脱落的涡在天窗后沿的上方逃逸,几乎没有撞击天窗后沿,侵入车内的涡量非常小,则车内的脉动压力较弱,从而使声场得到较大程度较低,在监测点峰值声压为91.2 dB,其对应频率为25 Hz。故优化后的导流板能够使乘员耳旁的峰值声压得到大幅度的降低。其主要原因是导流板安装的角度对周期性涡脱落运动的轨迹有很大的影响,如图16中所示,而涡脱落运动的轨迹决定了涡撞击天窗后沿的程度,从而引起车内脉动压力程度不同。
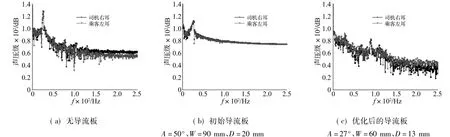
图17 监测点声压频谱Fig.17 Sound pressure level at the monitor’s point
6 结论
本文主要研究了某轿车的天窗风振噪声特性,并对天窗的附加装置—开槽天窗导流板进行了优化设计。其主要内容如下:
(1)对天窗开启时的风振噪声特性进行了仿真分析,得到了天窗风振噪声的频率及声压级,揭示了天窗风振噪声的形成机理,即呈现周期性的涡由生成、脱落、破碎等一系列运动而生成。
(2)针对天窗风振噪声,介绍并分析了几种降低天窗风振噪声的方法。在对各方法的优缺点比较之后,进一步确定开槽导流板作为进一步优化的对象。
(3)首先选取开槽天窗导流板外形及安装特征的三个参数(angle、width和depth)为设计变量,以驾驶员及副驾驶乘员耳旁声压级的加权值为目标函数值。通过试验设计方法,选择优化拉丁超立方抽样方法对设计变量和优化目标进行主效应和交互效应分析。采用优化拉丁超立方抽样方法所确定的试验方案计算结果,并采用Kriging模型用于构建近似模型。采用多岛遗传算法进行全局寻优,得到符合条件的最优解:27°(angle),13 mm(depth),60 mm(width),通过 CFD 仿真,结果显示优化后的导流板相对于初始导流板在驾驶员右耳处峰值声压降低了25.1 dB,相比降低了21.6%,降噪效果非常明显。由此可以说明,采用这种低成本高效率优化设计方法,可以更好地满足当前汽车产业对于汽车气动造型开发的要求。
(4)对天窗风振噪声而言,导流板安装的角度决定了涡脱落运动的轨迹,从而导致脱落的涡量撞击天窗后沿的幅度不同,引起车内脉动压力幅度不同。
[1]谷正气,肖朕毅,莫志姣.汽车风振噪声的CFD仿真研究现状[J].噪声与振动控制,2007,4:65-68.GU Zheng-qi,XIAO Zhen-yi,MO Zhi-jiao.Review of CFD simulation on vehicle wind buffeting[J].Noise and Vibration Control,2007,4:65 -68.
[2]Bodger W K,Jones C M.Aerodynamic wind throbin passenger cars[R].SAE Technical Paper 640797,1964.
[3]Aspinall D T.An empirical investigation of low frequency wind noise in motor cars[R].UK:MIRA report,1966.
[4] Nelson P A,Halliwell N A,Doak P E.Fluid dynamics of a flow excited resonance,PartⅡ:flow acoustic interaction[J].Journal of Sound and Vibration,1983,91(3):375-402.
[5] Ota D K,Chakravarthy S R,Becker T,et al.Computational study of resonance suppression of open sunroofs[J].Journal of Fluids Engieering,1994,116(4):877 -882.
[6]Karbon K,Kumarasamy S.Computational aero-acoustics applications in automotive design[C].First MIT Conference on Computational Fluid and Solid Mechanics,2001.
[7] An C F,Singh K.Optimization study for sunroof buffeting reduction[R].SAE Technical Paper,2006 -01 - 0138.
[8]An C F,Singh K.Sunroof buffeting suppression using a dividing bar[R].SAE Technical Paper,2007 -01 -1552.
[9]汪怡平,谷正气,杨雪,等.汽车天窗风振噪声数值模拟与控制[J].中国公路学报,2010(6):108-114.WANGYi-ping,GUZheng-qi,YANGXue,et al.Numerical simulation and control of automobile sunroof buffeting noise[J].China Journal of Highway and Transport,2010(6):108-114.
[10]黄磊.汽车天窗风振问题的研究[J].噪声与振动控制,2009,2:38 -41.HUANG Lei.Study of sunroof buffeting noise of automobiles due to wind load[J].Noise and Vibration Control,2009,2:38-41.
[11]康宁,王晓春.天窗对轿车内部流场及气动噪声的影响[J].航空动力学报,2010,25(2):354 -358.KANG Ning,WANG Xiao-chu.Influence of sunroof on flow field and aerodynamic noise inside the passenger compartment of the car[J].Journal of Aerospace Power,2010,25(2):354-358.
[12]胡亚涛,薛永飞,陈军,等.车辆天窗气动噪声的数值分析与实验研究[J].工程热物理学报,2011,32(4):589-592.HU Ya-tao,XUE Yong-fei,CHEN Jun,et al.Numerical simulation and experimental study of vehicle aerodynamic noise from open sunroof[J]. Journal of Engineering Thermophysics,2011,32(4):589 -592.
[13] Ffowcs Williams J E,Hawkings D L.Sound generation by turbulence and surfaces in arbitrary motion[J].Philosophical Transactions of the Royal Society America,1969,264(1151):321-342.
[14]汪怡平.汽车气动噪声分析与控制[D].长沙:湖南大学,2009.
[15] Karbon K J,Singh R.Simulation and design of automobile sunroof buffeting noise control[C]//Proceedings of the 8th AIAA/CEASAeroacoustics Conference & Exhibit,2002.
[16]欧健,姚疆,张勇,等.车内噪声对驾驶员心理特性影响的实验研究[J].噪声与振动控制,2009,5:105 -107.OU Jian,YAO Jiang,ZHANG Yong,et al.Experimental study on the effect of interior noise of vehicles on driver’s psychological character[J].Noise and Vibration Control,2009,5:105 -107.
[17] McKay M D,Beckman R J,Conover W J.A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J].Technometrics,1979,21(2):239 -245.
[18] Krige D G.A statistical approach to some mine valuation and allied problems on the Witwatersrand[M].University of the Witwatersrand,1951.
[19] Nestor V Q,Raphael T H,Wei S,et al.Surrogate-based analysis and optimization[J]. Progress in Aerospace Sciences,2005,41(1):1 -28.
[20] Holland J H.Genetic algorithms[J].Scientific American,1992,267(1):66-72.
[21] Wang J F,Wu Y Z,Pefiaux J.Decentralized multi-point optimization algorithms for multi-airfoil design in aerodynamic[J].Journal of Astronautics,2003,24(1):71 -77.
[22] Hoist T L.Genetic algorithms applied to multi-objective aerodynamic shape optimization[R].Chicago:NASA/TM -05 -212846,2005.
[23] Deb K. Multi-objective optimization using evolutionary algorithms[D].Wiley,Chichester,UK,2001.
[24] Jeong J,Hussain F.On the identification of a vortex[J].Journal of Fluid Mechanics,1995,285(1):69 -94.
