桥梁新型横向金属阻尼器研究

沈 星，倪晓博，叶爱君

(同济大学 土木工程防灾国家重点实验室，上海 200092)

对于桥梁结构，可采用的抗震体系主要有两类。一类是延性抗震体系［1］，在地震作用下，桥梁的弹塑性变形、耗能部位位于桥墩，上部结构、上下部结构连接构件(支座)以及桥梁基础，不受损伤，在弹性范围内工作。另一类是减隔震体系，在地震作用下，桥梁的耗能部位位于桥梁上、下部连接构件(支座、耗能装置)，上部结构、桥墩和基础不受损伤，基本在弹性范围内工作。而桥梁抗震规范推荐的减震装置包括整体型减隔震装置和分离型减隔震装置，后者由橡胶支座和各种阻尼器组合而成。

在各类阻尼器中，金属阻尼器以其滞回耗能性能稳定、形式变化多样及成本经济等优点得到了结构工程师的青睐。Kelly等［2］研究开发了软钢阻尼器，并从此在建筑工程中掀起了金属阻尼器的研究热潮。软钢阻尼器的形状各种各样，但主要耗能模式可以归为扭转型、弯曲型和滚弯型三种［3］。具体构造如图1所示。

在上述各种形式的金属阻尼器中，X形和三角形为基本构件的金属阻尼器具有沿高度范围内全截面屈服耗能的特点，耗能效率高，得到了较多的研究和应用。美国学者针对建筑工程，提出了X型和三角形金属阻尼器的构造，并进行了理论和试验研究［4－7］。

而在桥梁工程中，开发应用的金属阻尼器种类相对较少，主要是弯曲型的。在Rangitikei Rail Bridge的基础隔震部件中应用了扭转梁式钢阻尼器［8］。王君杰等［9］发明了可滑移柱形软钢阻尼装置，并在桥梁结构中得到运用。E型钢阻尼器［10］也已经在国内很多桥梁中得到了应用。李建中等［11］将X型弹塑性阻尼器引入桥梁中，主要作为弹塑性挡块使用，并对X型弹塑性阻尼器进行了拟静力和振动台试验，研究表明，X型弹塑性阻尼器具有很好的耗能能力，但是在复杂的传力条件下，可能会发生扭转或各板的不同步破坏。

图1 各种软钢阻尼器构造图Fig.1 Configuration of all kinds of different mild steel damper

目前，国内适用于桥梁纵向减震的装置较多，而擅长解决桥梁横向减震问题的阻尼器则很少。由于桥梁在正常使用状态下会发生比较大的纵向变形，所以即使是为解决横向抗震问题而设置的减隔震装置，也需要适应较大的纵向变形，而且耗能能力不会受纵向变形的影响。这意味着桥梁横向金属阻尼器需要采用悬臂式构造，其纵向能够适应桥梁的变形。同时金属阻尼器在复杂接触条件下力的传力模式要明确，并且还要各块板之间的受力的同步性很好，这样才能充分发挥金属阻尼器的耗能特性。因此，有必要提出一种耗能能力好、能适应纵向变形并具有在复杂接触条件下具有很好传力特性的新型桥梁横向金属阻尼器，并进行相关研究。

本文首先从桥梁结构横向抗震需求出发，对桥梁横向金属阻尼器提出相应的性能要求，然后在现有钢阻尼器研究成果的基础上，提出一种适用于桥梁横向的金属阻尼器。然后阐明该金属阻尼器的力学性能，并提出这种金属阻尼器的优化设计方法。最后，制作金属阻尼器试件，进行拟静力试验，验证阻尼器构造的有效性，以及滞回耗能能力。

1 桥梁横向金属阻尼器的设计

桥梁横向抗震对金属阻尼器提出了几点要求:①具有很好的滞回耗能能力和较大的位移能力;② 能够很好地适应桥梁纵向的较大变形且性能不受影响;③由于桥梁主梁横向复杂的振动特性要求金属阻尼器在复杂接触条件下具有很好的传力特性;④ 金属阻尼器的力学性能要明确，所以要求金属阻尼器的构造简单。为此，需要研发桥梁结构横向抗震专用金属阻尼器。

文献［4－7］已经验证了三角形钢板和X形钢板具有沿高度范围内全截面屈服耗能和具有理想的滞回耗能特性，以及针对建筑工程提出了相应的金属阻尼器构造，并在房屋抗震加固中得到运用。在一般建筑工程中，结构的惯性力沿高度基本均匀分布，抗震设计主要是控制层间位移和基底剪力，金属阻尼器一般在层间设置。而桥梁结构的惯性力主要集中在上部结构，惯性力通过支座传递给下部结构，金属阻尼器配合支座使用以减小墩底剪力并控制墩梁间位移。所以相对建筑工程而言，桥梁金属阻尼器的设置空间有限，强度和位移能力要求较高。此外，房屋结构中使用的金属阻尼器可以采用简单的铰接模式，以满足其在一个方向发生滞回耗能作用，而在另一个正交方向固定约束即可，而桥梁横向金属阻尼器还需满足桥梁纵向的较大变形，需要对约束方式和传力构造进行仔细研究。

考虑到桥梁结构和建筑结构的区别以及X型弹塑性阻尼器对不均匀荷载的抗扭失效，并结合前面桥梁横向对金属阻尼器提出的抗震要求，本文以三角形为基本构件，提出了一种能够满足桥梁横向抗震需求的金属阻尼器，其具体构造如图2所示:

图2 桥梁横向金属阻尼器三维图Fig.2 Three-dimensional map of metallic damper for bridge in transverse direction

这种金属阻尼器以三角形钢板为基本构件，在地震作用下，沿高度范围内全截面屈服耗能，以达到材料滞回耗能利用率的最大化。三角形钢板采用悬臂构造，在上顶板的钢挡块两侧设置聚四氟乙烯滑板，同时可以通过调整钢挡块的纵向尺寸，来很好地适应桥梁纵向变形。三角形钢板顶部放置半球形钢传力键，这样即使在地震过程中主梁和桥墩的相对运动比较复杂，钢传力键也能与上顶板上的钢挡块保持点接触，很好地适应各种复杂的传力条件，使三角形钢板在地震过程中的传力路径非常明确。

三角形钢板可以采用桥梁工程中常用的Q235或Q345钢材，钢板底部焊接在下底板上，下底板通过螺栓栓接在墩顶、盖梁或系梁上。上钢挡块焊接在上顶板上，上顶板通过螺栓栓接在主梁底。金属阻尼器可提前工厂预制生产，然后现场安装，安装过程跟一般支座的安装方法类似。

2 桥梁横向金属阻尼器设计方法

桥梁横向金属阻尼器的最优设计，应根据阻尼器的基本力学性能，以及桥梁的抗震需求，形成约束函数，在满足各种约束函数的条件下，以用钢量最少为目标函数，来确定桥梁横向金属阻尼器几何参数及数目。

2.1 桥梁横向金属阻尼器的力学性能

首先给出本金属阻尼器的受力模式及相关几何参数，具体标示如图3所示。

图3 金属阻尼器受力模式图Fig.3 Force mode of metallic damper

地震荷载F通过半球形传力键作用到三角形钢板的顶点，离三角形钢板顶点x处截面边缘的应力为:

可见沿三角形钢板高度范围内每个截面的最大应力和应变以及曲率是保持一致的，这样所有三角形钢板在地震作用下同时进入塑性，使其的耗能利用率达到最大。

由公式1可知，当截面刚好达到屈服时，金属阻尼器所承受的地震力为:

每个截面屈服时的曲率为:

将屈服曲率进行两次积分，就可以得到三角形钢板屈服时的顶点位移:

根据公式2和4可以得出本金属阻尼器全截面屈服时的屈服刚度:

根据桥梁横向的抗震需求，金属阻尼器在横向应具备一定的位移能力，由文献［8］可知，三角形钢板的位移能力可近似取10－15倍的屈服位移或根据试验得出。在对金属阻尼器的初步的设计中，可以选取10－15倍的屈服位移作为位移能力的预估值，待确定三角形钢板的几何参数后，由试验获得其实际的位移能力。

以上推导出来的桥梁横向金属阻尼器的屈服力Fy、屈服时顶点位移xy、屈服刚度Ky和位移能力将会作为约束函数来对金属阻尼器的几何参数和数目进行优化设计。

2.2 桥梁横向金属阻尼器的最优化设计方法

由桥梁横向金属阻尼器的力学性能可知，金属阻尼器的屈服位移取决于三角形钢板的高度和厚度，高度越高，厚度越薄，屈服位移越大;屈服刚度取决于三角形钢板的数目、板宽、厚度和高度，高度和厚度的变化与屈服位移相反，板宽和板数越大，屈服刚度越大;屈服力的变化趋势与屈服刚度一致，同时还与材料的屈服强度成正比。

桥梁横向金属阻尼器首先需要满足大位移能力的要求，然后还需考虑横向抗风刚度要求，需要金属阻尼器提供满足抗风所需的横向抗风刚度，以及满足横向在正常使用功能状态下所需要提供的固定支座横向承载力等。同时，桥梁横向金属阻尼器中的三角形钢板为不受焊接残余应力的影响以及保证上顶板钢挡块不与三角形钢板发生碰撞，三角形钢板之间需要保持一定距离，一般取5倍以上板厚。这样，在边墩、盖梁或系梁顶部有限的空间内需要确定能够放置三角形钢板的最大数目。

根据以上力学性能可知，各个几何参数之间相互影响，同时桥梁对金属阻尼器的承载力和刚度也提出了相应要求。因此需要用最优化理论来得到满足桥梁横向抗震需求的金属阻尼器几何参数最优值。

约束函数列式为

目标函数设定为三角形钢板的用钢量最小以达到控制成本的目的，用三角形钢板的总体积最小来表示:

这样就可以通过最优化理论［12］，利用Matlab编程得到满足桥梁横向抗震需求所需要的用钢量最小的金属阻尼器参数:三角形钢板高度、宽度、厚度和初始的板数。下面给出六组在不同水平承载力范围和位移能力要求下时，用这种优化方法得到的优化参数，如下表1所示。其中各参数变化范围控制在高度H小于0.7 m、板宽小于0.7 m、板厚小于0.05 m以内。

表1 参数优化算例Tab.1 Example of parameter optimization

得到最优化的参数后，可通过试验得出一块三角形钢板或者一组金属阻尼器的位移能力以及双线性本构关系。最后通过在初始三角形钢板板数基础上，在拟用桥梁的有限元模型中进行阻尼器参数分析，以得到满足桥梁横向抗震需求的金属阻尼器数目。

3 桥梁横向金属阻尼器拟静力试验

为了验证横向金属阻尼器的构造以及耗能能力，论文模拟地震时阻尼器的受力状态，设计并进行了拟静力试验，并与有限元分析结果进行了比较。

3.1 拟静力试验方案

根据桥梁横向的抗震需求，设计了两组几何参数相同但材料不同的三角形钢板试件，每组由三片三角形钢板组成。材料选用桥梁结构中常用的一级钢和二级钢，材料选用Q345－B的试件编号记为A，材料选用Q235－B的试件编号记为 B。试件几何参数及用Abaqus建立板壳模型得出的理论值列表于2，如下表所示。

表2 试件参数表Tab.2 Parameter table of two specimen

拟静力试验在同济大学地震工程馆内完成，水平加载利用水平液压作动器(MTS，15 t)进行往复循环加载，水平加载千斤顶通过在上顶板侧面预留的4根M16的锚栓进行连接。由于作动器连接处有球铰，会产生六个方向的自由度，并不能保证只发生水平运动。因此将上顶板四周往下伸出四块工字钢，工字钢底部采用轴承滚轮，使其在地面上铺设的钢轨上滑动。同时在上顶板顶部安装2.5 t的压重铅块，以保证上顶板不发生翘曲。由于上顶板与地面是滚动摩擦，产生的摩擦力很小，而且还可以通过空推上顶板得到滚动摩擦力来修正作动器水平推力，具体加载如下图4所示。

每块三角形钢板一侧贴有15片应变片，应变片的布置及应变片编号如下图5所示。

本次试验采用变幅、等幅混合位移控制的加载方式，采样频率1次/秒，每级加载位移做3次加载循环。开始的位移幅值分别为 ±5 mm、±10 mm、±15 mm、±20 mm、±30 mm、±40 mm、±50 mm，加载频率为0.03 Hz;然后位移幅值为 ±60 mm、±80 mm、±100 mm、±120 mm，加载频率为 0.02 Hz;以后每级增加±20 mm，加载频率为0.01 Hz，直至试件破坏。

图4 加载系统示意图Fig.4 Schematic diagram of loading system

3.2 试验结果分析

3.2.1 滞回曲线数据分析

由于半球形传力键与上顶板钢挡块下侧预留高度不足，试件A推到160 mm位移时，半球形传力键在推往作动器拉伸一侧时即将滑出，而此时金属阻尼器构件没有出现破坏现象。因此将加载方案改为向作动器收缩方向单向加载。当推到200 mm位移时，这一侧的半球形传力键也出现快滑出钢挡块的现象，加载停止。而此时试件A并没有出现强度降低和构造破坏的现象。此后试件B调整了半球形传力键与钢挡块的高度，当试件B循环推到200 mm时出现同样出现上述问题后，加载方案改为向作动器收缩侧单向加载。直到推到240 mm时，金属阻尼器出现强度下降，加载停止。试件A、B在加载过程中的滞回曲线以及骨架曲线，如图6所示。

由图6中试件A和B的滞回曲线和骨架曲线可以得到:本金属阻尼器的滞回曲线比较丰满，骨架曲线近似于双线性。说明本金属阻尼器可以用双线性本构来模拟其在地震过程中的滞回特性。试件B加载到240 mm时，并没有出现结构性的破坏，但是水平推力开始下降，从而标志金属阻尼器达到破坏状态。但是试件A加载到200 mm时，并没有出现结构性的破坏和水平推力下降现象，只是因为半球形传力键即将滑离上顶板钢挡块而停止加载。由试件A的数据和前面的理论推导可知，试件A应该可以获得比试件B更大的位移能力。由以上分析可知:两个试件的漂移率(最大位移能力/高度)均大于50%，说明本金属阻尼器装置使得材料的塑性利用率高，位移能力大。

通过有限元Abaqus程序建立试件A和B的板壳模型来模拟试验中的滞回曲线，如图7所示。由图7可知，用有限元程序Abaqus可以大致模拟整个试验过程中滞回曲线的趋势，Abaqus得到的滞回曲线在小位移时与试验相比水平推力稍偏大，在大位移时水平推力稍偏小，但整体的误差相差不大。两个试件在大位移时，滞回曲线回到原点时会存在一小平台段后在下降，这是由于半球形传力键和上顶板钢挡块之间有间隙造成的短时间空推。由有限元程序得到试件A中Q345－B钢板的硬化率为0，试件B中Q235－B钢板的硬化率为0.02。可见本金属阻尼器采用这两种材料时的硬化率还是比较小的，在对阻尼器进行初步设计时，钢材也可采用理想弹塑性本构关系进行模拟，得出的墩顶横向位移是偏安全的。

图5 单块板应变片布置图(单位:mm)Fig.5 The layout schematic diagram of strain gauge on single plate(Unit:mm)

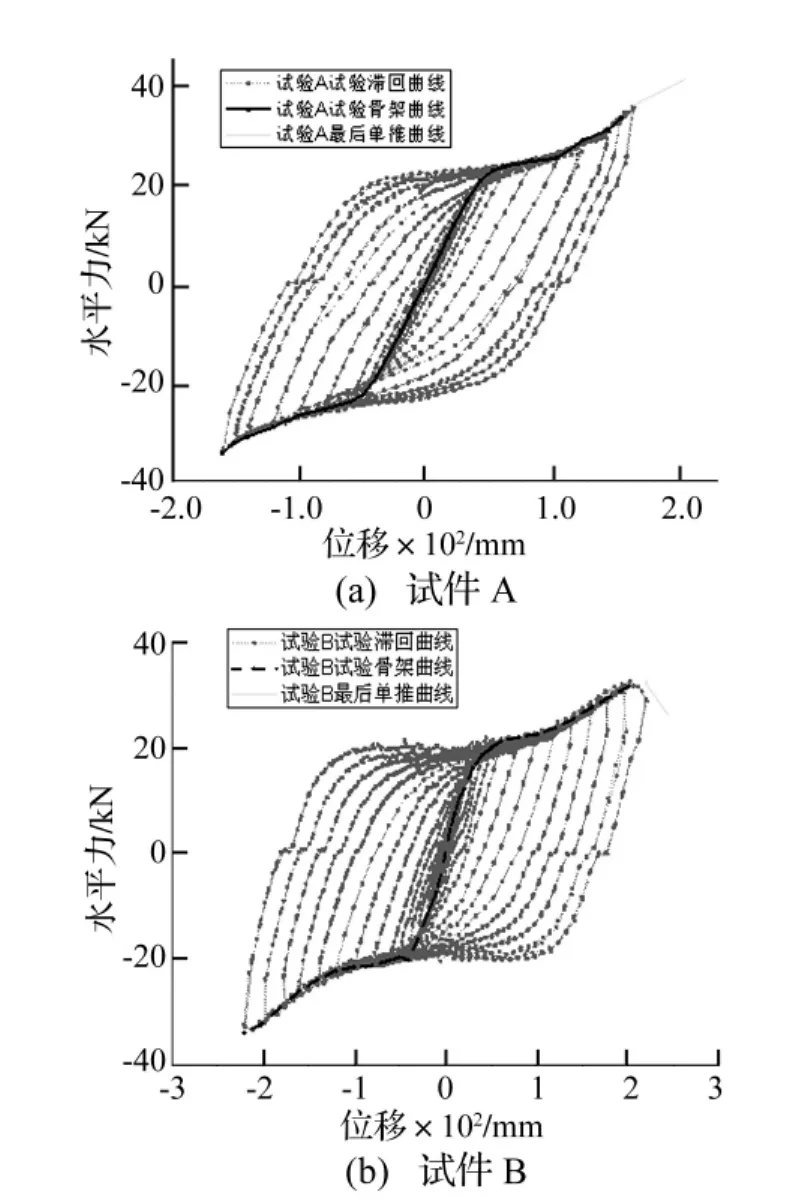
图6 滞回曲线和骨架曲线Fig.6 Hysteresis curves and skeleton curves

图7 有限元Abaqus程序模拟试验滞回曲线Fig.7 The simulation of testhysteresis curve by Finite Element Program Abaqus

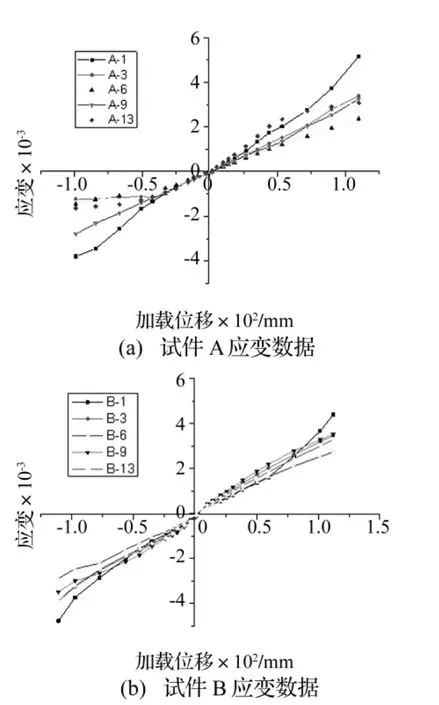
图8 单块板中轴线上测点应变变化Fig.8 The measured strain change on central line of single plate

3.2.2 应变片数据分析及试验现象说明

当试件处于小位移时，作动器的扭转并不明显，这时同一高度上的应变片数据相差不大。然而当试件推到较大的位移时，作动器会产生扭转运动，同一高度上的应变片会发生不规律的变化。因此为避免扭转对三角形钢板应变的影响，下面给出试件A和B其中一块板在中轴线上测点1、3、6、9、13应变随位移的变化规律，由于位移过大后，应变片超过了测量量程，其结果是失效的，所以结果仅提出作动器位移在100 mm之前晋宁循环推倒的试验数据，如图8所示。

由图8可以看出，三角形钢板应变在小位移时，底端的应变最大，且各个位置的应变相差不大;而在大位移时，顶端的应变最大，其它位置处的最大应变是从上到下逐渐增大分布，且总体的大小相差不大。大位移时顶端应变最大的原因可能是因为半球形传力键和里面垫板之间产生了摩擦力的缘故。然而对整个三角形钢板而言，沿高度范围内的大部分应变变化基本同步，进一步从试验中验证了三角形钢板沿高度范围内同时达到屈服耗能的特点。

图9 试件B破坏时变形图Fig.9 The destruction deformation picture of specimen B

图10 作动器和加载架变形图Fig.10 The deformation picture of actuator and load frame

图9 中给出了试件B最后达到破坏时的变形状况。由图中可知，金属阻尼器一直到最后发生水平推力下降破坏过程中，各块三角形钢板的变形保持同步。

当试件B加载到160 mm时，由于作动器横向没有采取固定措施，导致作动器在此时发生严重横向偏转，从而使上顶板加载装置的一根工字钢支撑架与下底板发生碰撞导致其产生严重变形，如图10所示。

由图10中可以看出，当作动器发生严重横向偏转时，本适用于桥梁横向金属阻尼器并没有发生扭转破坏，正好验证本金属阻尼器在复杂接触条件下的适应能力很好。在实际地震中，上顶板钢挡块与半球形传力键之间的接触也不能保持是完全平动，其间也会伴随不均匀接触碰撞。通过试验过程中的这一个小插曲，正好验证了本金属阻尼器具有在复杂接触条件下的适应能力。

4 结论

本文提出了一种新型桥梁横向金属阻尼器，以三角形钢板为基本构件，采用半球形钢传力键适应复杂的传力条件，通过半球形钢传力键与聚四氟乙烯滑板的滑动来适应桥梁的纵向变形，提出了金属阻尼器的优化设计方法，并制作阻尼器试件进行了拟静力试验，结果表明:

(1)桥梁横向金属阻尼器构造简单，力学性能明确，通过合理的设计能够满足桥梁结构抗震性能要求。

(2)桥梁横向金属阻尼器具有很好的滞回耗能特性，其滞回模型可用等效双线性模型模拟。

(3)桥梁横向金属阻尼器具有较大的位移能力(漂移率大于50%)，不同三角形钢板具有很好的同步性，并且在复杂的接触条件下具有很好的适应能力。

［1］Priestley M J N.Performance based seismic design［J］.Engineering Structures，2000，25(14):1803 －1813.

［2］Kelly J M，Shinner R I，Heine A J.Mechanisms of energy absorption in special devices for use in earthquake resistant structures［R］.Bulletin of N.Z.Society for Earthquake Engineering，1972，5(3)，63－87.

［3］Camara A.Seismic behavior of cable-stayed bridges:design，analysis and seismic devices［D］.Department of Continuum Mechanics and Theory of Structures.Universidad Politécnica de Madrid，10，2011，1－475.

［4］ Aiken I D，Nims D K，Whittaker A S，et al.Testing of passive energy dissipation systems［J］.Earthquake Spectra，1993，9(3)，335－369.

［5］ Perry C L，Fierro E A，Sedarat H，et al.Seismic upgrade in san francisco using energy dissipation devices ［J］.Earthquake Spectra，1993，9(3):559－579.

［6］ Whittaker A S，Bertero V V，Thompson C L，et al.Seismic testing of steel plate energy dissipation devices ［J］.Earthquake Spectra，1991，7(4)，563－604.

［7］Tsai K C，Chen H W，Hong C P，et al.Design of steel triangular plate energy absorbers for seismic-resistant construction［J］.Earthquake Spectra，1993，9(3)，505－528.

［8］Skinney R I，Tyler R G，Heine A J，et al.Hysteresis dampers for the protection of structures from earthquakes［J］.Buiietin of New Zeaiand National Society for Earthguake Engineering.1980，13(1):22 －26.

［9］王君杰，王志强，章小檀，等.可滑移柱形软钢阻尼装置及其在桥梁上的应用［P］.CN200810204146.2.上海:同济大学;上海材料研究所，2010－06－23.

［10］高峰利.新型金属阻尼器的减振机理及其在桥梁抗震中的应用［D］.长沙:湖南大学，2008，1－78.

［11］方圆.汶川地震典型简支梁桥震害分析及横向限位装置研究［D］.上海:同济大学，2012，1－174.

［12］解可新，韩立兴，林友联.最优化方法［M］.天津:天津大学出版社，2001，1－344.