Sharp Inequalities for the Euler-Mascheroni Constant

-， -

(School of Mathematics and Informatics, Henan Polytechnic University,Jiaozuo, Henan 454000, China)

1 Introduction

The Euler-Mascheroni constantγ=0.577215664… is defined as the limit of the sequence

Dn=Hn-lnn,

(1.1)

whereHndenotes thenth harmonic number, defined forn∈N∶={1,2,3,…} by

Several bounds forDn-γhave been given in the literature [1-7]. For example, the following bounds forDn-γwas established in [2,3]:

The convergence of the sequenceDntoγis very slow. By changing the logarithmic term lnnin (1.1), some quicker approximations to the Euler-Mascheroni constant were established in [8-16]. For example, DeTemple[8]proved in 1993 that

(1.2)

where

Recently, Chen[9]obtained the following sharp form of the inequality (1.2): For all integersn≥1, then

(1.3)

with the best possible constants

In 1997, Negoi[10]proved that the sequence

(1.4)

is strictly increasing and convergent toγ. Moreover, the author proved that

(1.5)

Recently, Chen and Mortici[11]obtained the following sharp form of the inequality (1.5): For all integersn≥1, then

(1.6)

with the best possible constants

Also in [11], the authors proved that forn∈N,

(1.7)

with the best possible constants

In this paper, by changing the logarithmic term ln(4n) in (1.7), we present sharp inequality for the Euler-Mascheroni constant.

TheoremFor all integersn≥1, let

Then

(1.8)

with the best possible constants

2 Lemmas

The Euler-Mascheroni constantγis deeply related to the gamma functionΓ(z) thanks to the Weierstrass formula:

The logarithmic derivative of the gamma function:

is known as the psi (or digamma) function. The successive derivatives of the psi functionψ(z):

are called the polygamma functions.

The following lemmas are required in our present investigation.

(2.1)

and

(2.2)

with

whereBkare Bernoulli numbers defined by

From (2.2), we obtain forx>0,

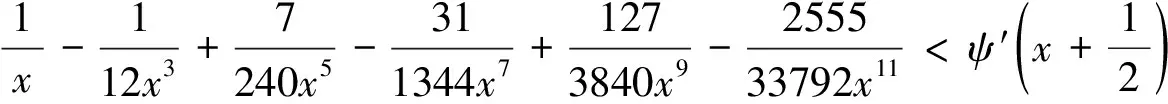
(2.3)

Lemma2Forx≥2, let

(2.4)

Then

(2.5)

and

(2.6)

ProofConsider the functionF(x) defined by

Applying the second inequality in (2.3), we obtain that forx≥2,

with

G(x) =38149418294893+309603910615856(x-2)+580284311908092(x-2)2

+482792790621464(x-2)3+204943551011683(x-2)4

+43378335655200(x-2)5+3614861304600(x-2)6.

Hence,F′(x)<0 forx≥2, and we have

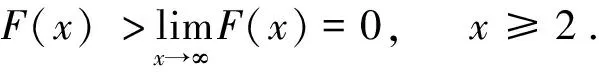
This means that the inequality (2.5) holds forx≥2.

It is well-known that letx>-1, then forα<0 orα>1,

(1+x)α≥1+αx,

(2.7)

the equal sign holds if and only ifx=0.

Applying the inequality (2.7), we obtain from (2.5) that forx≥2,

The proof of Lemma 2 is complete.

3 Proof of Theorem

It is well-known[18,p.258]that

Thus, the inequality (1.8) can be written as

θ1≥f(n)>θ2,n∈N,

where

withh(x) defined in (2.4).

asx→∞. It follows from (2.1) that

We then obtain that

Further, we find that

which implies

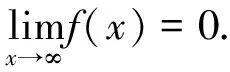
Direct computation yields

In order to prove our Theorem, it suffices to show that the sequence (f(n)) is strictly decreasing forn∈N. Differentiatingf(x) and applying (2.3) and (2.6) yield, forx≥4,

where

g(x) =10010655865312+21800267033016(x-4)+17008581298487(x-4)2

+6513883623680(x-4)3+1326804177680(x-4)4

+137952967680(x-4)5+5748040320(x-4)6.

Hence,f′(x)<0 forx≥4.

Direct computation yields

f(1)=0.114501384…,f(2)=0.078266339…,

f(3)=0.057606492…,f(4)=0.045564402….

Hence, the sequence (f(n)) is strictly decreasing for alln∈N. The proof is complete.

[References]

[1] Tims S R, Tyrrell J A. Approximate evaluation of Euler’s constant [J]. Math. Gaz., 1971, 55 (391):65-67.

[2] Rippon P J. Convergence with pictures [J]. Amer. Math. Monthly, 1986, 93 (6): 476-478.

[3] Young R M. Euler’s Constant [J]. Math. Gaz., 1991, 75: 187-190.

[4] Tóth L. Problem E3432 [J]. Amer. Math. Monthly, 1991, 98 : 264.

[5] Tóth L. Problem E3432 (Solution) [J]. Amer. Math. Monthly, 1992, 99 (7): 684-685.

[6] Anderson G D, Barnard R W, Richards K C, Vamanamurthy M K, Vuorinen M. Inequalities for zero-balanced hypergeometric functions [J]. Trans. Amer. Math. Soc., 1995, 347 (5): 1713-1723.

[7] Alzer H. Inequalities for the gamma and polygamma functions [J]. Abh. Math. Sem. Univ.Hamburg,1998,68:363-372.

[8] DeTemple D W. A quicker convergence to Euler’s constant [J]. Amer. Math. Monthly, 1993,100(5):468-470.

[9] Chen C P. Inequalities for the Euler-Mascheroni constant [J]. Appl. Math. Lett., 2010, 23 (2): 161-164.

[10] Negoi T. A faster convergence to the constant of Euler [J]. Gazeta Matematicǎ, seria A, 1997,15:111-113 (in Romanian).

[11] Chen C P, Mortici C. Limits and inequalities associated with the psi function [J]. Appl. Math.Comput.,2013, 219 (18):9755-9761.

[12] Vernescu A. A new accelerated convergence to the constant of Euler [J]. Gazeta Matematicǎ, seria A, 1999, 273-278.

[13] Villarino M. Ramanujan’s harmonic number expansion into negative powers of a triangular number[J].J.Inequal. Pure Appl. Math., 2008, 9(3): Article 89. Available online at http:∥www.emis.de/ journals/JIPAM/images/245_07_JIPAM/245_07.pdf.

[14] Chen C P. Inequalities and monotonicity properties for some special functions [J]. J. Math. Inequal.,2009, 3(1): 79-91.

[15] Mortici C.On new sequen cesconverging towards the Euler-Mascheroni constant [J].Comput.Math.Appl.,2010,59(8): 2610-2614.

[16] Mortici C. Improved convergence towards generalized Euler-Mascheroni constant [J]. Appl. Math.Comput., 2010, 215(9) :3443-3448.

[17] Allasia G, Giordano C, PecariJ. Inequalities for the gamma function relating to asymptotic expansions [J]. Math. Inequal. Appl., 2002, 5(3): 543-555.

[18] Abramowitz M, Stegun I A .Handbook of mathematical functions with formulas, graphs,and mathematical tables, applied mathematics series 55[M]. Ninth printing.Washington, D.C.: National Bureau of Standards, 1972.