高超音速二元机翼的颤振响应研究
2014-09-17叶欣陈予恕
叶欣 陈予恕
(1.中国航天科工集团第九总体设计部,武汉 4 30040)(2.哈尔滨工业大学航天学院,哈尔滨 1 50001)
高超音速二元机翼的颤振响应研究
叶欣1†陈予恕2
(1.中国航天科工集团第九总体设计部,武汉 4 30040)(2.哈尔滨工业大学航天学院,哈尔滨 1 50001)
在飞机结构设计中,非线性因素不可避免.本文以高超音速流下的,在俯仰自由度上含有立方非线性刚度的二元机翼为研究对象,采用平均法及颤振理论研究了超高速飞机机翼的非线性动力学行为,并通过数值计算验证了理论计算的正确性,给出了对比分析结果.
高超音速, 非线性, 二元机翼, 平均法
引言
随着我国高超声速飞行器的迅速发展,飞行器气动弹性设计越来越受到关注.对于一定结构的弹性体,其空气动力将会随着气流流速的增加而增加,而结构的弹性刚度却与气流的速度无关,所以存在一定的临界风速,在这种速度下结构是不稳定的[1].从稳定性这个角度出发,将这种不稳定性可区分为静不稳定性和动不稳定性,前者主要指扭转变形,后者主要指颤振.传统的气动弹性分析主要在频率域内进行[2].Theodorson运用非定常理论导出了在不可压缩流中作简谐运动的二元平板的气动力表达式,后人结合V-G法、P-K法等颤振分析方法,广泛地用于低速气动弹性问题的计算和分析,基于线化理论的升力面方法也被广泛地用来计算机翼作简谐运动的频域气动力[3].频域方法的优点是可以方便地与传统控制理论相结合,能够给出系统整体特性的描述,并且计算量少.缺点是由于运用了很多的线性化假设,很难处理跨音速、高超音速、大攻角等含有强气动力非线性系统的大变形、间隙、摩擦等结构非线性的气动弹性问题[4,5].随着计算机性能的大幅提高,系统的时域仿真技术被广泛地用于气动弹性的响应模拟[6].由于时域气动弹性的建模比较方便,相对于频域而言更容易实现结构模块、气动模块(气动力求解)和控制模块的结合,时域方法已经成为解决非线性气动弹性的主流方法[7,8].
1 非线性动力学建模
本章所用的模型是具有两个自由度,弦长为2b、宽度为一个单位长度的二元翼段.两个自由度分别是:机翼刚心的垂直位移h,机翼绕刚心的转角α.翼段分别由一个线弹簧和一个盘旋弹簧连接在刚心E点,其中俯仰方向的盘旋弹簧带有立方非线性刚度.如图1所示,E点在翼弦中点后εb处,重心到弹性轴的距离以xαb表示.
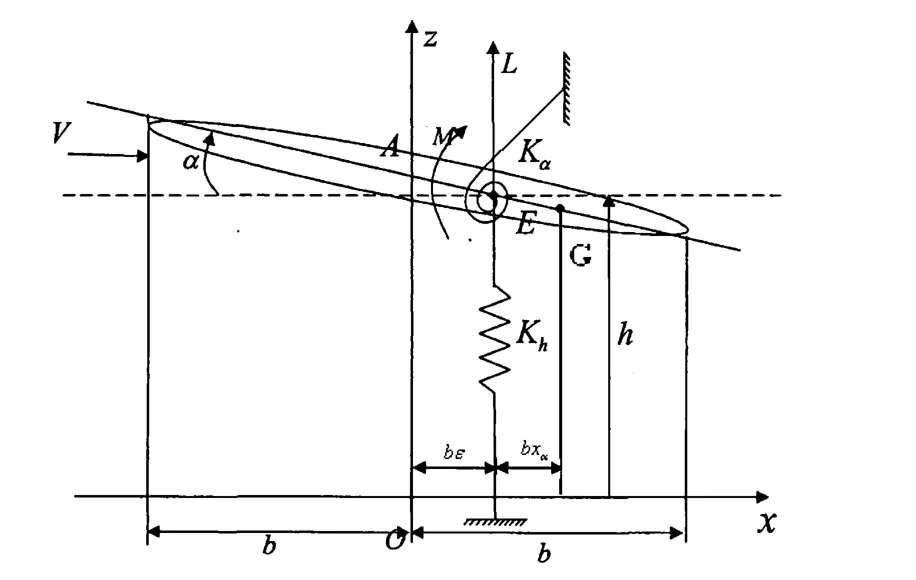
图1 二元机翼的动力学模型Fig.1 the dymanic model of the two-degree-of-freedom airfoil
运用拉格朗日方程[7]可以得到系统的无量纲方程为:
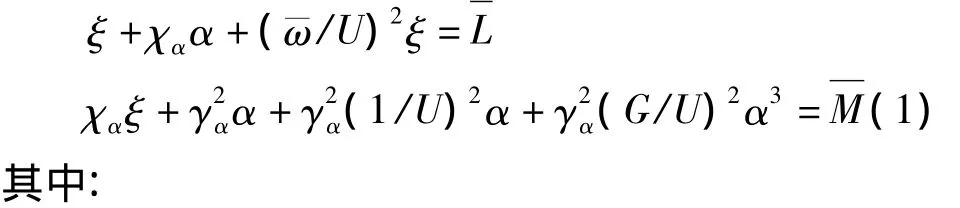
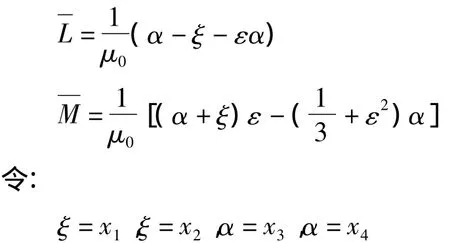
取: χα=0.25=0.25=1/2
忽略ε的二次项,于是可以得到系统的典则方程:

通过平均法求解,可以得到标准方程:
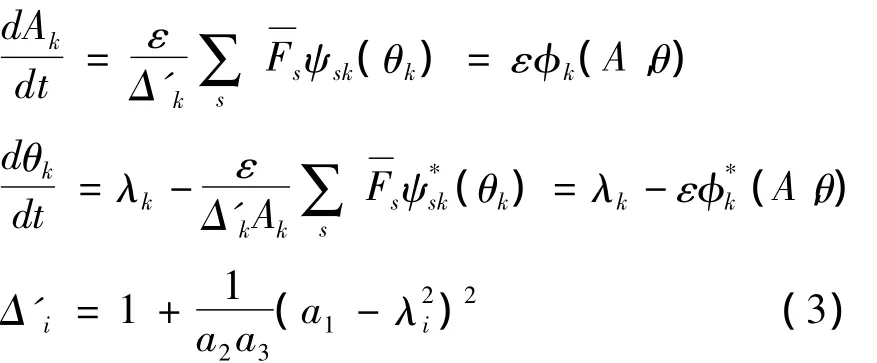
对方程(3)采用K-B变换:
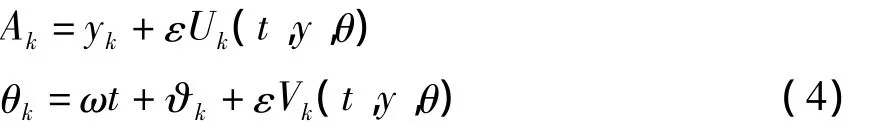
要求新的变量yk,ϑk的导数为
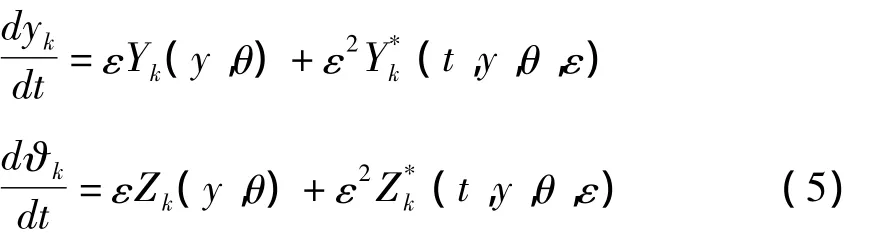
其中 Yk,Zk不显含 t ,Uk,Vk,和为以2π 为周期的周期函数.
只考虑ε的一次项,经计算可以得到系统的定常解方程:
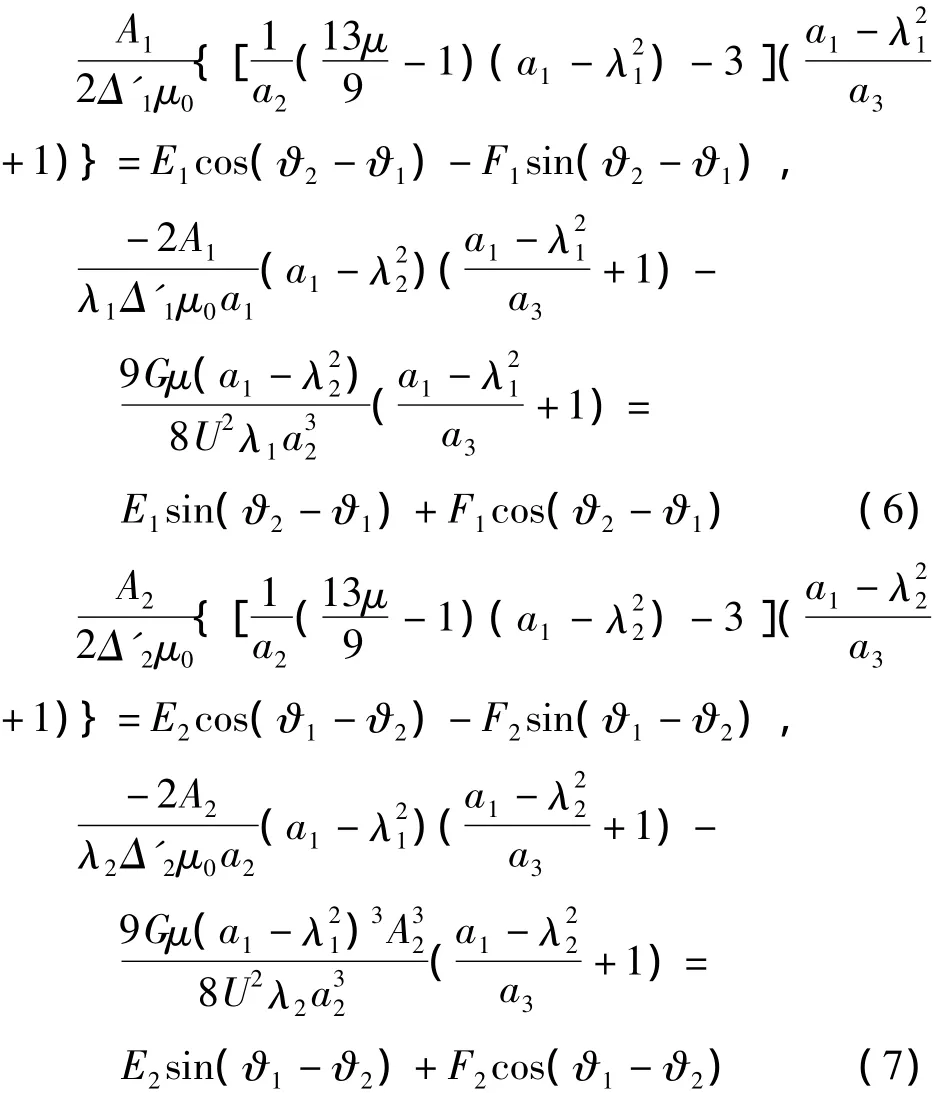
连立式(6)、(7),于是可以得到:
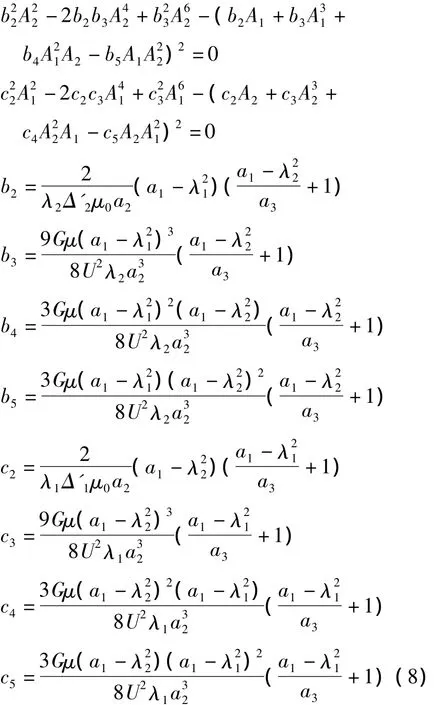
2 理论与数值分析对比
从理论上分析系统的共振响应特性,采用分析参数如下:
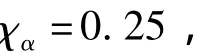
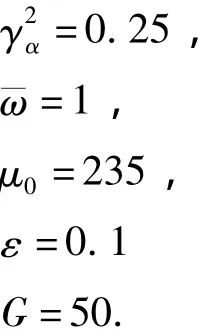
将参数代入式(8),可以分别得到系统沉浮自由度以及俯仰自由度的共振响应随速度的变化曲线,图2显示的是当无量纲速度V在区间15<V<65上时,系统的主共振响应随V的变化关系曲线.
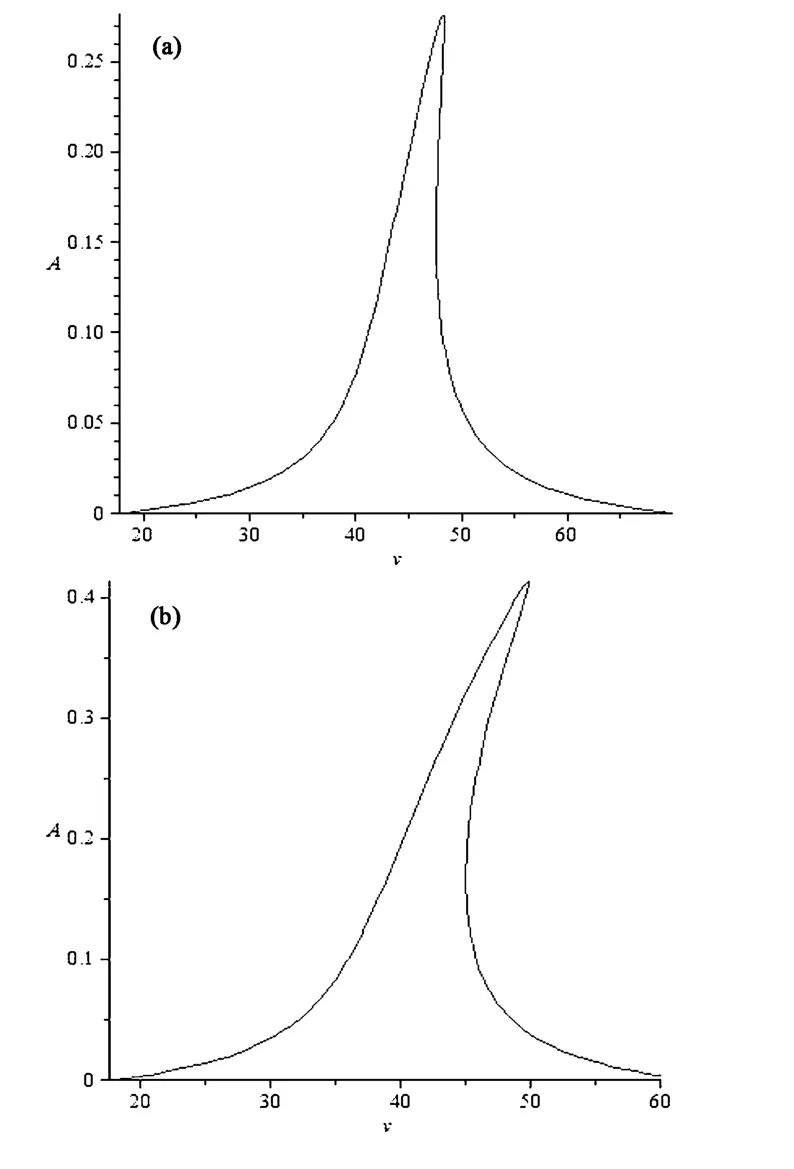
图2 系统的偏航(a)、俯仰(b)共振响应随速度的变化曲线Fig.2 the yaw(a)and pitch(b)resonant response with different speed
从图中可知:振幅A从V=18开始一直随V增大而增加,至V=48时,此时沉浮自由度幅值与俯仰自由度幅值同时出现峰值,幅值分别为0.26,0.41,随后逐渐减小,并出现了多值现象.
采用数值计算方法分析系统颤振幅值与速度的相关特性,如图3、图4所示.
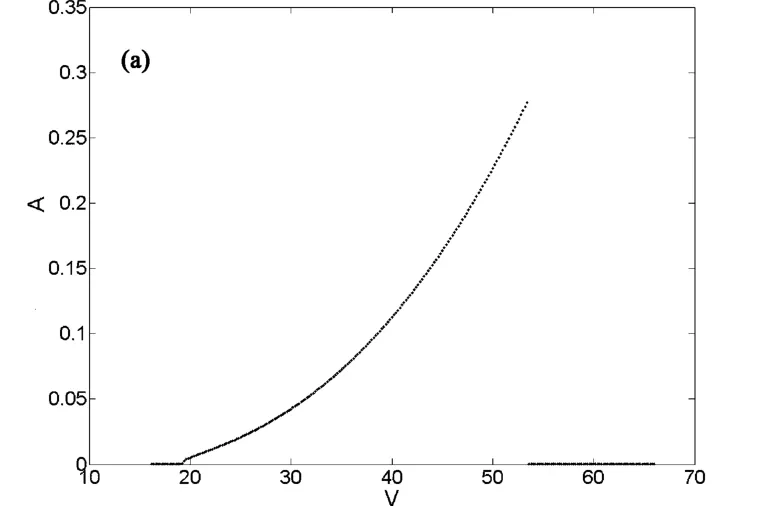
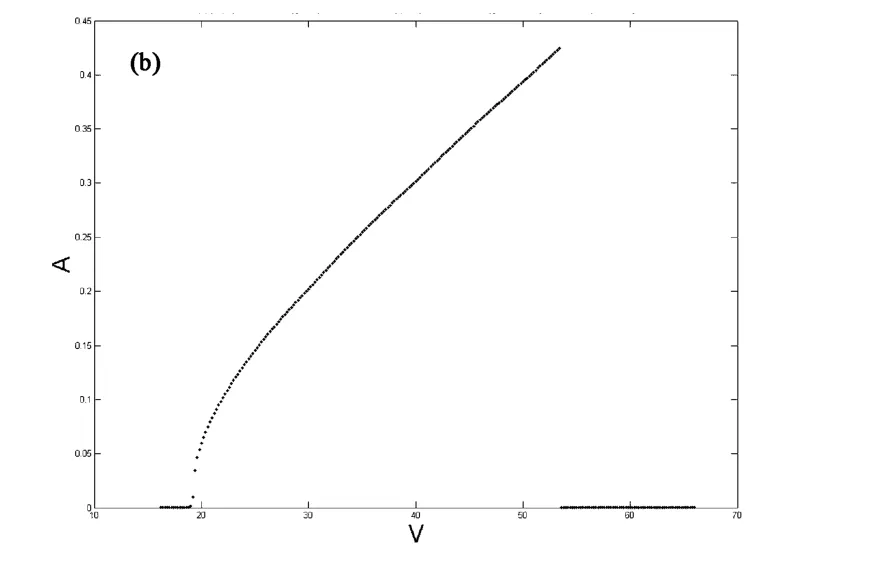
图3 V从正向计算时系统偏航(a)、俯仰(b)幅值随速度变化曲线Fig.3 yaw(a)and pitch(b)amplitude curve when speed from the forward calculation
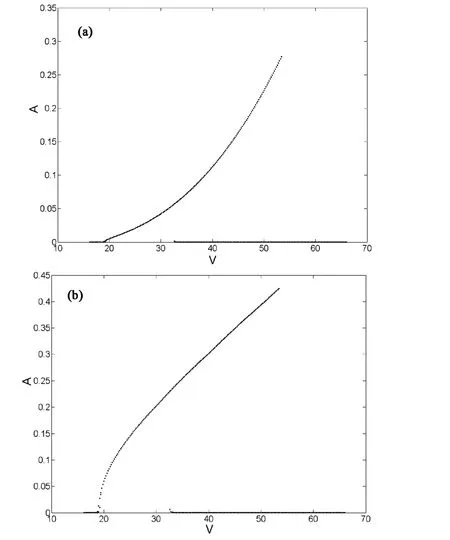
图4 V从反向计算时系统偏航(a)、俯仰(b)幅值随速度变化曲线Fig.4 yaw(a)and pitch(b)amplitude curve when speed from the reverse calculation
对比理论和数值模拟的颤振曲线,可以得到以下分析结果:
(1)理论计算的沉浮自由度最大幅值0.26比数值模拟的最大幅值0.273偏小;俯仰自由度最大幅值0.41比数值模拟的最大幅值0.4384偏小,但基本接近.
(2)数值模拟振幅在无量纲速度达到53.34时,突然下降至0,而不再进行颤振,而理论结果则在无量纲速度经过48后,开始逐渐减小.
(3)结合反向计算模拟的变化曲线很好的反应了解析结果的多值现象,但幅值的跳跃点还是有一定的差异.
(4)平均法计算的共振响应随速度的变化曲线与数值模拟的结果从定性和定量的角度都吻合得较好.
3 结论
本文以高超音速为来流的环境下,在俯仰自由度带有非线性立方刚度的二元机翼为模型,主要研究了系统的颤振问题.分别运用平均法及数值计算求得了系统的共振响应随速度的关系曲线,对比结果表明理论与数值计算结果吻合得较好,系统颤振幅值与颤振区间基本相符.
运用平均法理论得到的解析结果还可以作解的稳定性分析,从而更好的解释系统的非线性特性,本文的结论可以为高超音速机翼的动力学分析提供一定的理论依据.
1 Librescu L,Chiocchia G,Marzocca P.Impliactions of cu
bic physical/aerodynamic non-linearties on the character of the flutter instability boundary.International Journal of Non-Linear Mechanics,2003,38:173 ~199
2 Bae J S,Lee I.Limit cycle oscillation of missile control fin with structural non-linearity.Journal of Sound and Vibration,2004,269:669 ~687
3 Abbas L K,Chen Q,O’Donnell K,Valentine D,Marzocca P.Numerical studies of a non-linear aeroelastic system with plunging and pitching freeplays in supersonic/hypersonic regimes.Aerospace Science and Technology,2007,11:405~418
4 Guo X Y,Mei C H.Application of aeroelastic modes on nonlinear supersonic panel flutter at elevated temperatures.Computers and Structures,2006,84:1619 ~1628
5 Bi Q S.Chaos crisis in coupled Duffing’s systems with initial phase difference.Physics Letters A,2007,369:418~431
6 Librescu L,Chiocchia G.Implications of cubic physical/aerodynamic non-linearities on the charater of the flutter instability boundary.International Journal of Non-Linear Mechanics,2003,38:173~199
† Corresponding author E-mail:yexinfeng@163.com
FLUTTER ANALYSIS OF 2-D AIRCRAFT WINGS IN SUPERSONIC FLOW
Ye Xin1†Chen Yushu2
(1.Ninth general design department,China Aerospace Science&Industry Corporation,Wuhan430040,China)(2.School of Astronautics,Harbin Institute of Technology,Harbin150001,China)
Non - linear factors cannot be avoided in the design of aircraft structures.In this paper,a two-degreeof-freedom airfoil and cubic stiffness nonlinearities in pitching degree-of-freedom operating in supersonic flight speed regimes has been analyzed.The averaging method and the theory of flutter were used to analyze the nonlinear dynamic system of the dualistic airfoil in the supersonic flow.Then the correctness of the theoretical calculation was verified by numerical calculation,and the analysis result was given.
supersonic, nonlinear vibration, 2-d aircraft wings, average method
19 June 2014,
22 July 2014.
10.6052/1672-6553-2014-048
2014-06-19 收到第 1 稿,2014-07-22 收到修改稿.
E-mail:yexinfeng@163.com
