参数振动主动控制系统研究*

傅晨宸 黄 迪山

(上海大学机电工程与自动化学院，上海 2 00072)

参数振动主动控制系统研究*

傅晨宸 黄 迪山†

(上海大学机电工程与自动化学院，上海 2 00072)

应用Liapunov－Floquet变换，将参数振动系统转换成一个时不变系统，结合极点配置法，构成一个控制品质稳定的振动主动控制系统．并以机翼与航空发动机转子耦合振动为例，叙述参数振动主动控制结构以及控制系统稳定性的仿真结果．

参数振动， Liapunov－Floquet变换， 极点配置， 主动控制， 航空发动机转子

引言

机械工程学中都存在着具有时变周期系数的参数振动系统．由于参数振动具有时变系数，对其的主动控制一直是一个具有挑战性的任务．其中最主要的问题是无法直接根据标准方法使用时变特征值来判断参数振动系统的稳定性［1］．使用平均法［2］可以对参数振动系统进行研究，但这种方法只适用于小变量的情况．继而Sinha提出的Liapunov－Floquet变换法［3］，通过变换将时变系统转换成时不变系统，从而对系统进行振动主动控制．此方法已成功地应用于倒立摆的振动主动控制的研究［4］．

本文将以机翼与航空发动机转子耦合振动为例，应用 Liapunov－Floquet变换法，结合极点配置法，对参数振动系统进行振动主动控制研究．

1 参数振动描述

考虑简谐激励频率与内部参数频率不同的参数振动情况，具有非线性项的参数振动系统方程为:

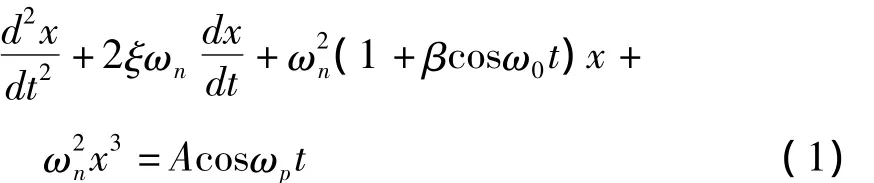
参数振动系统是一个强非线性系统．其中ξ为系统的阻尼比，ωn为系统的固有频率，β为常数，外部简谐激励频率为ωp，而系统参数频率则为ω0．

设y=［xx］T将式(1)改写为状态空间表达式:

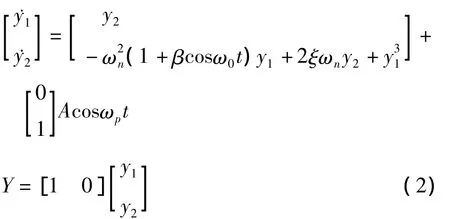
式(2)中有非线性项．在平衡位置y=0处对上述方程中的非线性项使用泰勒展开式进行线性化，可以得到线性化后的状态空间表达式为:

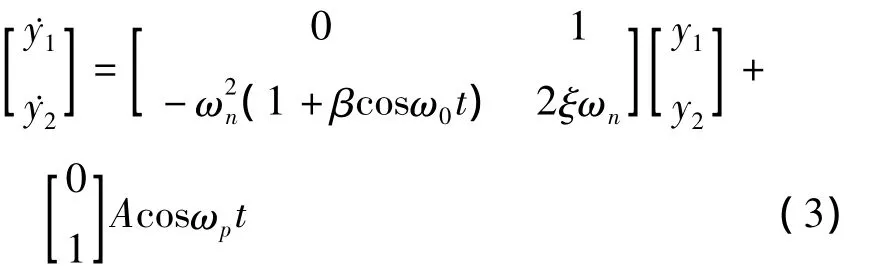
2 Liapunov－Floquet变换

利用Liapunov－Floquet变换法可以解决时变系统转换成常系数系统的问题．一般的T周期的Liapunov－Floquet数学变换(以下简称L－F变换)过程如下，若系统方程为:

对于系统(4)，引入周期为2T的L－F变换:

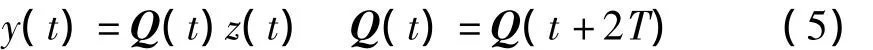
系统(4)变换成时不变系统:

其中R为常数矩阵，其表达式为:

Q(t)则是2T周期L－F变换矩阵:

其中φ为系统(4)的状态转移矩阵．

通过2T周期L－F变换，我们将得到常系数控制系统为:

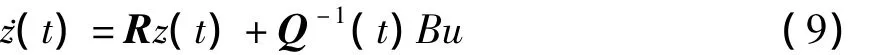
3 参数振动主动控制

对参数振动系统状态方程(4)，根据现代控制理论，采用Neumann级数［8］求解系统(3)的状态转移矩阵Φ(t)．t

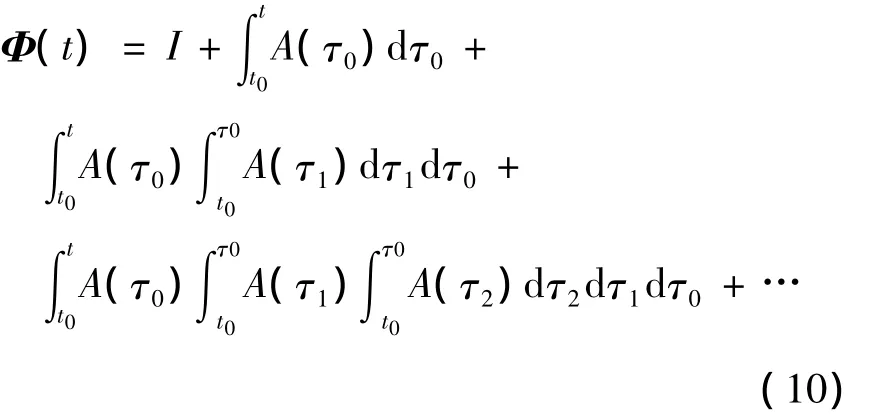
其中τ0，τ1为无物理含义的中间积分变量，对于系统(3)而言，积分下限为t0=0，积分上限为时间变量t．

在状态系统(3)中的参数为:阻尼系数ξ=0，系统固有频率为ωn=10(rad/s)，系统内周期变化参数频率为ω0=5(rad/s)，常数β=0．3．在计算过程中进行有限项进行积分运算，得到其时变状态转移矩阵φ(t):

时变状态转移矩阵φ(t)中各元素的数学表达式为:

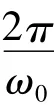
将式(13)代入式(7)得到L－F变换后的常数矩阵R:

将式(14)代入(8)得到在此情况下的L－F变换矩阵Q的表达式:

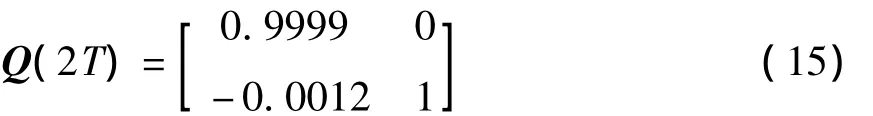
综上所述，将(14)和(15)代入(9)．原系统(1)线性化为:

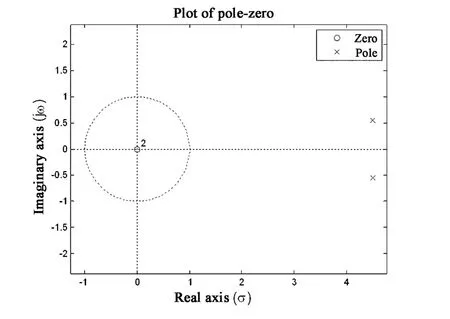
图1 极点配置前系统的零－极点图Fig．1 Plot of pole － zero for original system

从图1可以看出，系统(16)的两个极点分布于复平面的右半平面，系统在激励的作用下将产生增幅正弦振荡现象［9］．它可通过采用状态负反馈极点配置改善其稳定性．

由于控制系统的性能很大程度上取决于系统极点在复平面上的分布，因此，通过选择反馈增益矩阵，将闭环系统的极点恰好配置在复平面上所期望的位置，构建一个稳定性系统．对于系统(16)的状态空间表达式，引入状态反馈控制律为:

其中K为线性状态反馈矩阵，v为输入．则闭环控制系统状态空间表达式为:

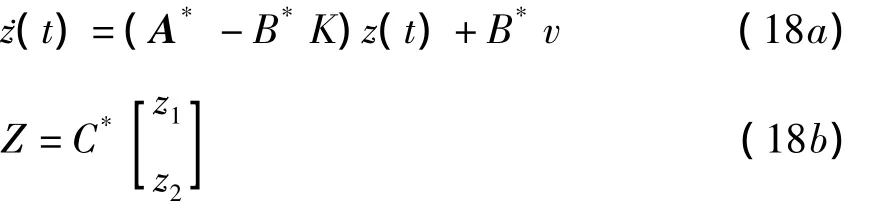
控制系统(18)矩阵为满秩，该系统完全可控．若建立一个稳定性系统，置系统的极点配置到复平面的左半面，而且位置不靠近单位圆．取理想极点为= －2+2i，= －2 －2i．极点配置后，特征多项式为:

通过线性变换，得到状态反馈矩阵K:

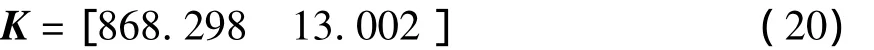
将状态反馈矩阵K代入式(17)得到极点配置后系统为:

极点配置后系统的零－极点图如图2所示，极点位置分布符合控制系统的稳定性条件．引入状态负反馈环节实现系统的零－极点重新分配．

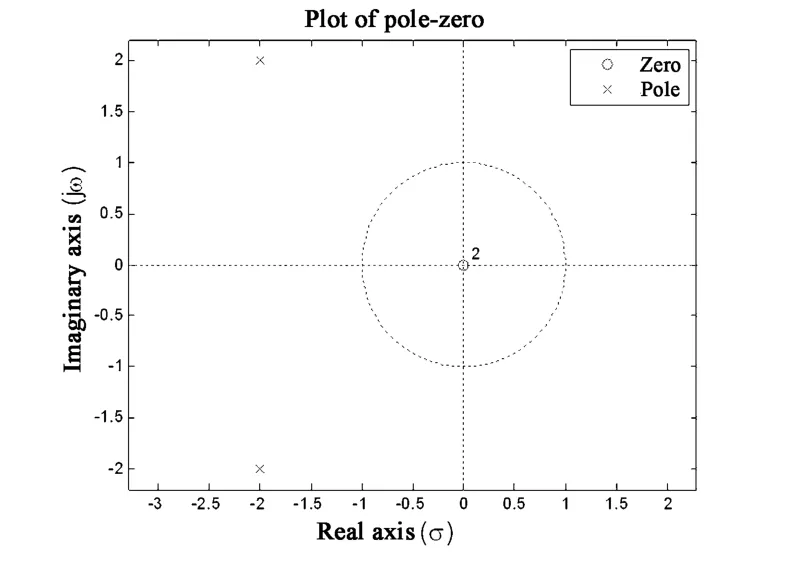
图2 极点配置后系统的零－极点图Fig．2 Plot of pole － zero after restting poles

4 参数振动主动控制应用

机翼与悬挂在其下方的航空发动机转子(如图3(a)所示)是飞机中的耦合结构．将机翼与航空发动机转子结构倒置后，建立如图3(b)所示的动力学模型．

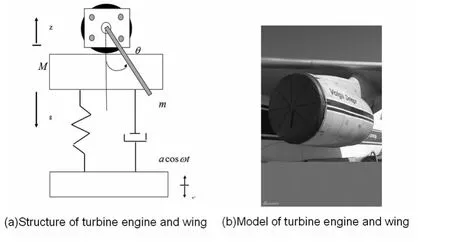
图3 机翼与航空发动机Fig．3 Turbine engine and wing

机翼所产生的颤振是动力学模型中的基础振动，对航空发动机产生耦合激励，若航空发动机转子为具有偏心的电机模型，则机翼和转子耦合动力学方程为:

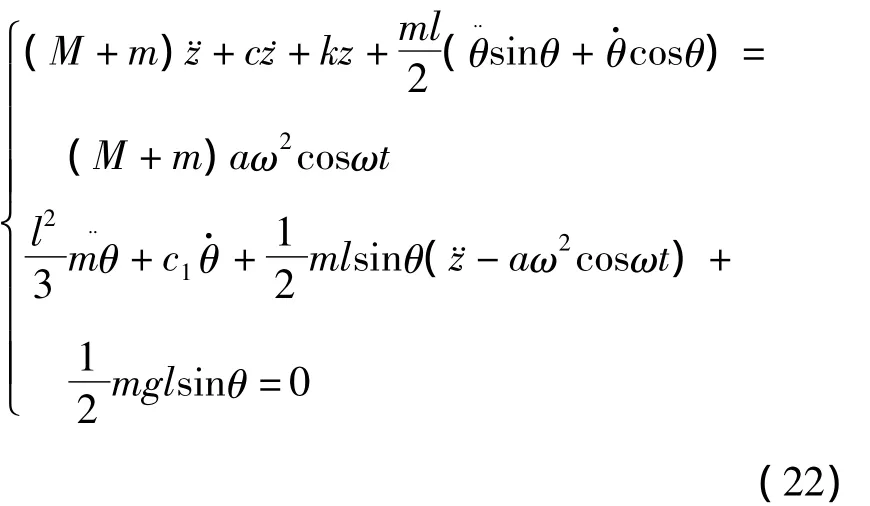
发动机转子扭振位移θ=θ0+φ是参数振动方程的变量，对转子扭振动扼制是航空动力关注的问题之一．

利用Liapunov－Floquet变换法可以解决时变系统转换成时不变系统的问题．由于系统的极点分布于复平面的右半平面，系统将在激励的作用下产生增幅正弦振荡现象，并且极点靠近单位圆，系统不稳定．

为了改善控制系统稳定性，在主动振动控制系统设计中，取理想极点为=－2+2i=－2－2i，并且选取状态反馈控制律为式(17)所示．通过极点分配，得到该系统的状态反馈矩阵向量K．构成的反馈闭环系统框如图4所示．

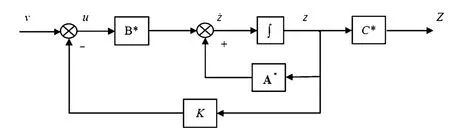
图4 状态负反馈闭环系统图Fig．4 Diagram of feedback control system

所建的主动控制系统结构示意如图5所示．其中φ(t)为角振动传感器测得的转子扭振动位移，z(t)为L－F变换后状态变量，K为状态反馈向量，v为系统输入．

图5 主动控制系统构成Fig．5 Active control for torsioanl vibtaion system

主动扭振控制系统阶跃响应性能如图6所示．从系统阶跃特性可知，响应经过上升后很快达到稳定，极点配置对系统稳定性起到了很好的效果．

5 结论

本文对机翼与航空发动机转子非线性参数振动系统模型，利用Liapunov－Floquet数学变换，将它转化成一个线性系统;采用极点配置方法，对变换后系统引入反馈环节，最后实现主动参数扭振动控制．所构成主动参数扭振动控制系统，对转子扭振起到了有效的扼制作用，并具有良好的稳定性．因此，进一步对其主动控制理论和实践的研究，可为改善飞机动力学特性研究提供了一种新的尝试．

1 Marghitu D B，Sinha S C，Boghiu D．Stability and control of a parametrically excited rotating system．Part I:Stability analysis．Dynamics and Control，1998，8:5 ～18

2 Anderson G L，Tadjbakhsh I G．Stabilization of Ziegler’s pendulum by means of the method of vibrational control．Journal of Mathematical Analysis and Applications，1989，143:198～223

3 Sinha S C，Pandiyan R，Bibb J S．Liapunov－Floquet transformation:computation and applications to periodic systems．Journal of Vibration and Acoustics，1996，118:209～219

4 Mori S，Nishihara H，Furuta K．Control of a mechannical system，control of a pendulum．International Journal of Control1976，23:673 ～692

5 王炜，张琪昌，田瑞兰．两自由度强非线性振动系统的渐近解及分岔分析，振动与冲击，2008，27(5):130～133(Wang W，Zhang Q C，Tian R l．Asymptotic solutions of strongly nonlinear two degrees of freedom vibration system and bifurcation analysis．Journal of Vibration and Shock，2008，27(5):130～133(in Chinese))

6 李友善．自动控制原理．北京:国防工业出版社．2005(Li Y S．Principles of automatic control．Beijing:National Defense Industry Publishing House，2005

7 于霞，刘建昌，李鸿儒．时变系统控制方法综述．控制与决策．2011，26(9):1281～1287(Yu X，Liu J C，Li H R．Methods of controlling time－varying systems．Control and Decision，2011，26(9):1281～1287(in Chinese))

8 王孝武，张晓江，现代控制理论基础．北京:机械工业出版社．2006(Wang X W，Zhang X J．Modern control theory．Beijing:Mechanical Industry Publishing House，2006(in Chinese))

9 吴宇．系统函数H(S)的极点位置分布对系统时域特性的影响．潍坊高等职业教育，2005，1(2):17～19(Wu Y．System time－domain characteristics’distribution on diffierent pole position of system function H(S)．Higher Vocational Education，2005，1(2):17～19(in Chinese))

10 肖建，张友刚．线形系统理论．成都:西南交通大学出版社，2011(Xiao J，Zhang Y G．Linear systems theory．Chengdu:Southwest Jiaotong University Publishing House，2011(in Chinese))

11 Sinha S C，Berlioz A，R Dufour．Bifurcation in a nonlinear autoparametric system using experimental and numerical investigations．Nonlinear Dynamics，2000，23:175～187

*The project supported by the National Natural Science Foundation of China(10872156，81071150)，and the Aviation Foundation of China(20111396011)

† Corresponding author E－mail:hdishan@shu．edu．cn

STUDY ON ACTIVE CONTROL FOR PARAMETRIC VIBRATION SYSTEM*

Fu Chenchen Huang Dishan†
(Shool of Mechtronical Engineering and Automation，Shanghai University，Shanghai200072，China)

A parametric vibration system was transferred into a linear time invariant system by applying the Liapunov－Floquet transform．After resetting the pole－zeroes position in the system，an active control for parametric vibration system was obtained with the stable response．A coupling vibration example of aero plane wing and rotor in a turbine engine was given，and active control structure for parametric torsional vibration and the simulation result of stable system were illustrated．

parametric vibration， Liapunov－Floquet transform， pole－zero reset， active control， turbine rotor

15 June 2014，

16 July 2014．

10．6052/1672－6553－2014－049

2014－06－15 收到第 1 稿，2014－07－16 收到修改稿．

*国家自然科学基金资助项目(10872156，81071150)，航空基金资助项目(20111396011)

E－mail:hdishan@shu．edu．cn