压缩感知在多载波EBPSK雷达中的应用

陈 鹏 吴乐南

(东南大学信息科学与工程学院，南京 210096)

压缩感知在多载波EBPSK雷达中的应用

陈 鹏 吴乐南

(东南大学信息科学与工程学院，南京 210096)

摘 要:将压缩感知(CS)技术应用于多载波相位编码脉冲雷达中，分析了该雷达的目标时延和多普勒频率估计以及不同频点散射系数估计的性能.对比了在不同目标数条件下采用BCoSaMP重构算法时EBPSK与BPSK的目标时延和多普勒频率估计性能，并估计了雷达的目标散射系数.仿真结果表明:基于CS的密集多载波雷达的目标检测性能优于正交多载波雷达，而且在正交与密集多载波条件下，EBPSK调制的目标检测性能优于BPSK调制;目标散射系数估计精度与信噪比呈对数关系，在低信噪比时EBPSK调制的目标散射系数估计性能优于BPSK调制.理论分析与仿真结果表明了CS技术在降低信号的采样频率方面的有效性和可行性.

关键词:多载波雷达;压缩感知;EBPSK;目标检测;BCoSaMP

宽带雷达具有较好的目标检测性能和较高的距离分辨率［1］，但高采样频率加重了接收端模数转换器(ADC)的负担，增加了系统复杂度.一些研究结果［2-5］表明将压缩感知(CS)技术应用在宽带雷达系统中，可以在低采样频率条件下实现雷达的目标检测，与传统技术相比，能进一步提升雷达的目标检测和分辨能力［4，6］.多载波雷达信号作为宽带雷达信号的一种，近几年得到了广泛的关注.与传统的步进频率宽带雷达信号相比，多载波信号的持续时间较短，对目标运动不敏感，因此比较适合用于高速目标的探测［7］.由于目标对不同频率电磁波的谐振系数不同，使得多载波雷达信号可以提供目标检测的频率分集增益［3］.

本文采用基于CS技术的多载波相位编码(MCPC)脉冲雷达系统对目标检测问题进行了研究，分析了子载波间隔与检测性能的关系;并根据目标散射系数估计与信道估计的相似性，将基于CS的信道估计算法［8］用于目标散射系数估计.针对目标时延和多普勒频率估计问题，由于目标在时延多普勒平面上的稀疏特性，本文采用文献［2，9-11］中提出的基于块稀疏的重构理论对目标的时延和多普勒频率进行了估计.

1 问题描述与建模

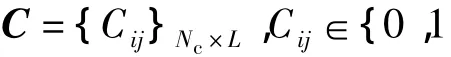
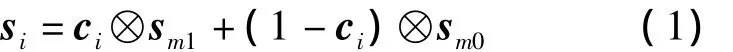
式中，ci为编码矩阵C的第i列;sm1与sm0分别为信息“1”和“0”调制波形的时域采样;⊗表示Kronecker积.则MCPC信号可表示为

假设目标对不同频率电磁波的散射系数为ξ={ξ0，ξ1，…，ξL－1}T，且时延 τ以及多普勒频率 β=fD/fc未知，则通过高斯白噪声信道后的雷达接收信号为

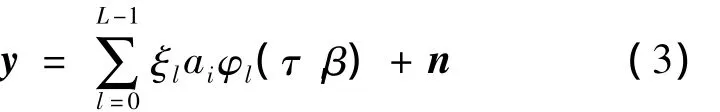
式中，φl(τ，β)为sl在时延以及多普勒频率分别为τ和β时对应的波形;n为高斯白噪声向量.将式(3)重写为矩阵形式:

式中，y=［y(t0)T，y(t1)T，…，y(tN－1)T］T，且 y(tn)=［y0(tn)，y1(tn)，…，yL－1(tn)］T;N为每个子载波信号的时域采样点数;矩阵 Φ=［Φ(t0，τ，β)T，…，Φ(tN－1，τ，β)T］T∈RLN×L包含了回波信号的时延和多普勒频率信息，且 Φ(tn，τ，β)=diag{φ0(tn，τ，β)，…，φL－1(tn，τ，β)};矩阵 A=diag{a}为不同子载波的权重.

由于时延多普勒平面的内在稀疏性，可将回波信号(4)建模为 CS中的块稀疏形式，设NG=NτNβ，从而将式(4)重写为

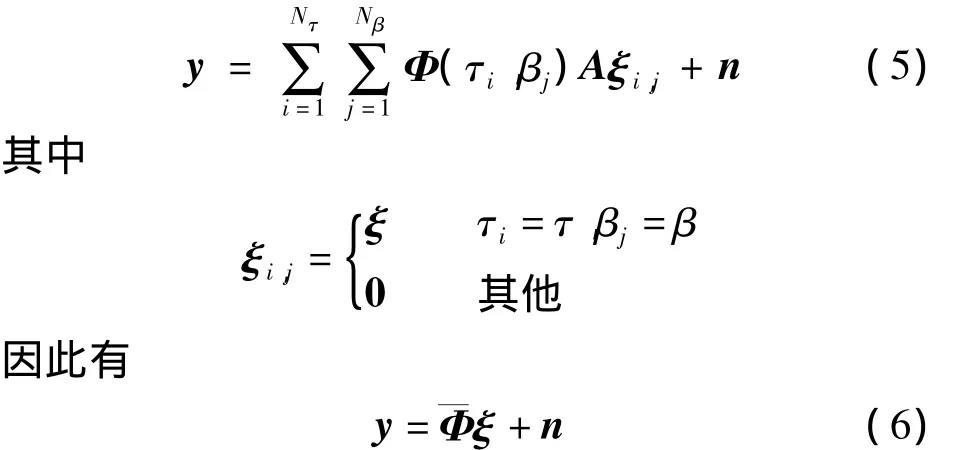
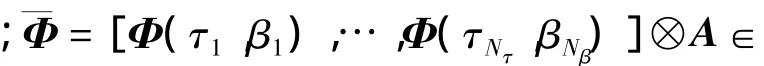
① 初始化估计值=(ξ)－，初始化余量r=y，i=0.

③重复步骤②直到满足终止条件，输出(ξ)+=.

本文采用相对均方误差来衡量目标散射系数估计的精确度，即

EBPSK 调制信号定义如下［12-13］:

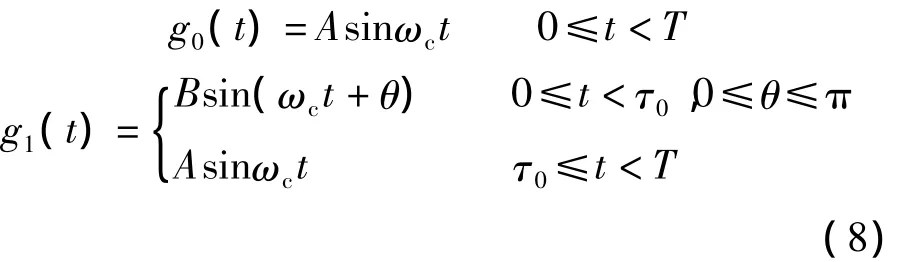
式中，T为调制符号时间长度;θ为信号“1”的跳变相位;ωc为载波角频率;τ0为跳变时间长度.

目标时延和多普勒频率估计只需估计出离散时延多普勒平面中目标的位置，而目标散射系数估计需要对各个载波频点的目标散射性能进行估计.图1和图2分别为不存在噪声时利用BCoSaMP算法得到的时延多普勒平面中目标位置估计以及目标散射系数的估计值，这里CS压缩比为9.566倍，从图中可知采用CS算法可以估计出所有目标时延和多普勒频率以及目标散射系数.

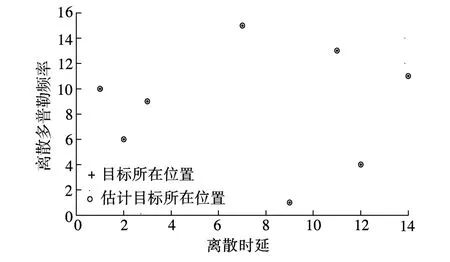
图1 目标在时延多普勒平面上的位置及位置估计值

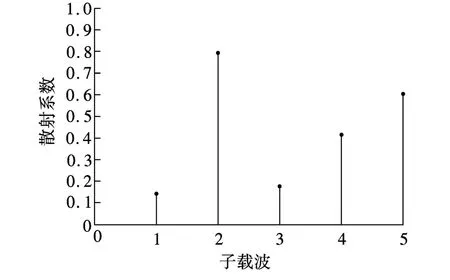
图2 不同频率的散射系数及其估计值

2 系统仿真结果

本文的仿真参数设置如下:雷达MCPC信号的调制方式为 EBPSK和 BPSK，编码矩阵 C={Cij}Nc×L，Cij∈{0，1}为随机矩阵，子载波编码长度Nc=5，子载波个数L=5，EBPSK调制占空比为1∶10，目标数为M，目标在离散时延多普勒平面上均匀分布，其中时延与多普勒频率离散点数分别为Nτ=15和Nβ=15，接收信号信噪比范围为SNR∈［－5，20］dB.CS 测量矩阵 Ψ∈RP×Q采用高斯分布随机矩阵，其中Q=LNG，P=O(LMlog(NG/M))，则目标反射波的压缩倍数为O(NG/［Mlog(NG/M)］)，在不同目标数下CS的降采样倍数如图3所示.由图可知，当目标数大于10时测量矩阵的压缩倍数较低，因此本文主要考虑目标数小于10的情况.

图3 不同目标数条件下CS的降采样倍数

2.1 不同目标数条件下的目标检测性能

当目标数不同且目标在时延多普勒平面上均匀分布时，采用BCoSaMP重构算法对目标的时延多普勒网格点进行估计，图4为不同目标数条件下采用EBPSK与BPSK调制时目标检测性能的对比.从图中可知当增加目标数时EBPSK调制会降低雷达的目标检测概率，而增加接收信号的信噪比可以明显提高检测概率，但仿真结果中也存在例外，即9个目标时的目标检测概率明显高于7个目标时的目标检测概率，而且BPSK调制可得到与EBPSK调制基本相同的结论.对比这2种调制方式可以发现子载波间正交时，EBPSK调制的多载波雷达脉冲信号的目标检测概率明显高于BPSK调制的目标检测概率.因此，在基于CS的时延多普勒估计中，EBPSK调制方式的性能优于BPSK调制.

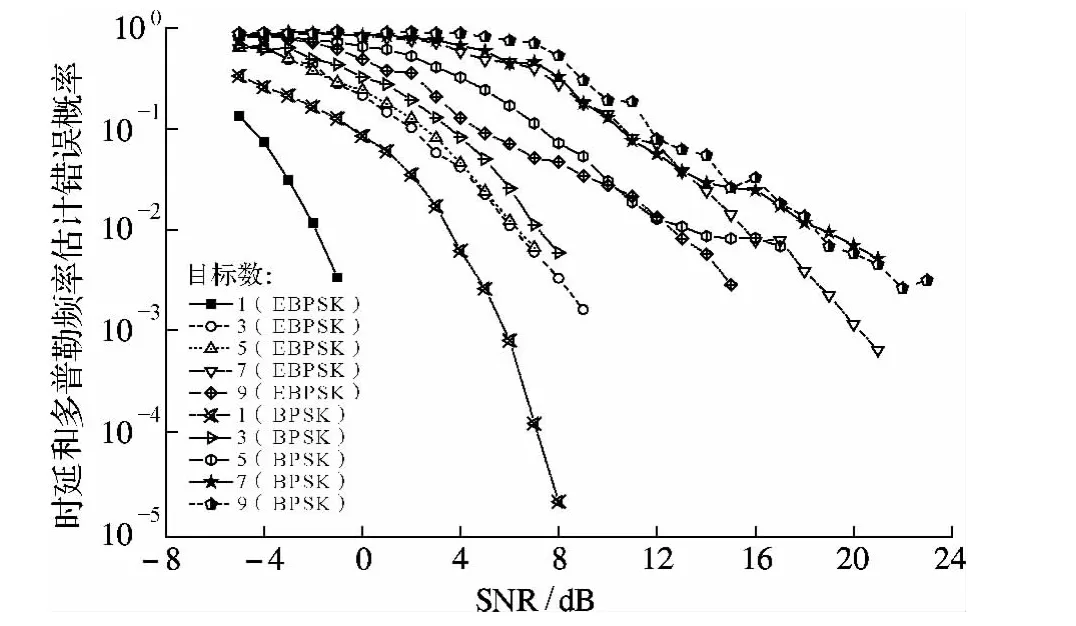
图4 EBPSK与BPSK调制在不同目标数条件下的对比

2.2 密集多载波条件下的目标检测性能

当雷达发送信号带宽为B=5/Tb时，如果子载波数超过5个，则其不再满足正交条件，本文对该条件下雷达的目标时延和多普勒频率的估计性能进行了仿真.图5为BPSK与EBPSK多载波雷达在不同子载波间隔条件下目标时延和多普勒频率估计性能的对比.当调制方式为EBPSK时，图5(a)为子载波间隔满足正交条件下的目标检测性能，图5(b)～(f)为子载波间隔小于正交条件下的目标检测性能.图5表明减小子载波间隔可提高目标检测性能，但并非子载波间隔越小越好，例如7个子载波的目标检测性能明显优于8个子载波的目标检测性能.在本文条件下发送信号的最佳子载波数为9个，相应的子载波间隔为Δf=5/(9Tb)＜1/Tb，这时雷达能获得较好的目标时延和多普勒频率估计性能.

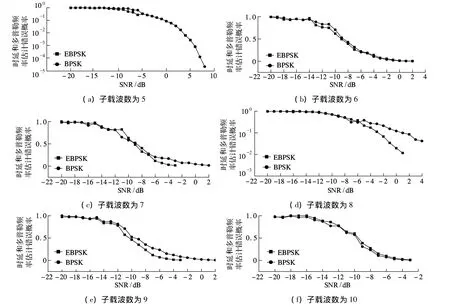
图5 BPSK与EBPSK多载波雷达在不同子载波间隔条件下目标时延和多普勒频率估计性能对比

采用BPSK调制时，当子载波间隔小于正交条件时，多数情况下目标时延和多普勒频率估计性能得到提高，除了图5(d)中子载波数为8的情况.当信噪比较低时密集多载波的目标检测性能优于正交多载波.虽然信噪比较高时密集多载波检测性能比正交多载波差，但是大多数情况下采用BPSK调制的密集多载波雷达信号，可提高雷达的目标时延和多普勒频率估计性能.在正交条件下(即图5(a)的5个子载波情况)，EBPSK的目标检测性能比BPSK稍好，而在非正交条件下，由于EBPSK功率谱比BPSK功率谱集中［14］，有利于进一步减小各个子载波间隔，因此EBPSK调制方式的目标检测性能与BPSK基本相同或更好.如子载波数为8和9时的EBPSK的目标检测性能明显优于BPSK，而子载波数为6，7和10时，EBPSK的目标检测性能与BPSK相差无几.因此多载波脉冲雷达使用CS算法对目标时延和多普勒频率进行估计时，采用EBPSK调制方式比BPSK调制方式有优势.

图6考虑了CS不同压缩比对目标时延和多普勒频率估计性能的影响.通常情况下目标的检测性能随着压缩比的减小而提高，但仿真结果表明对原始接收信号压缩10倍后的数据进行目标检测的性能比压缩12倍及16倍的还要差一些，但相差不大，都明显优于48倍压缩后的目标检测性能，而且较低压缩率会带来计算复杂度的增加，因此需要权衡系统目标检测精度提高所带来的系统复杂度的增加.

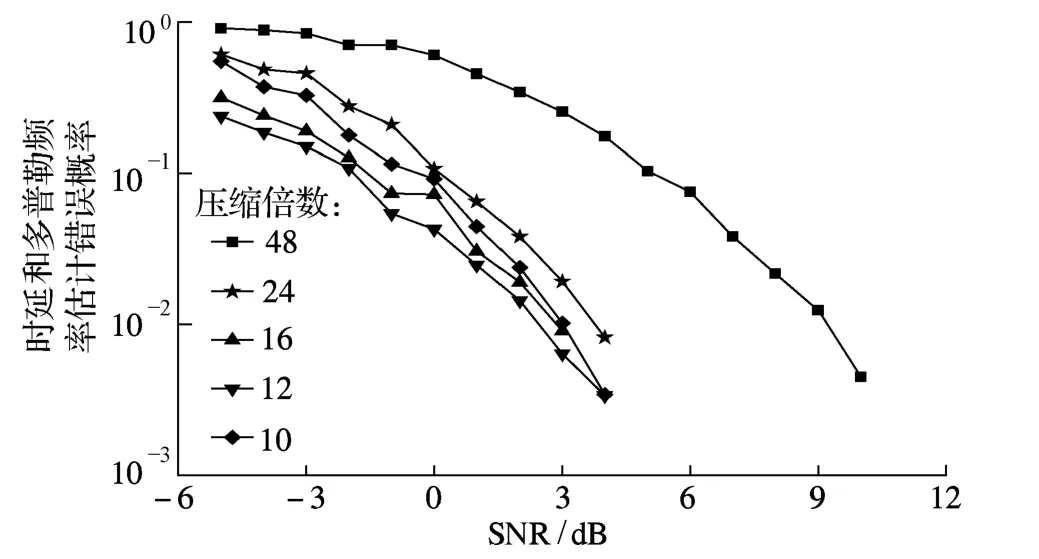
图6 CS不同压缩比对目标时延和多普勒频率估计的影响

2.3 目标散射系数估计

图7为采用CS算法对目标在不同频率处的散射系数进行估计的相对均方误差.从图中可看出，相对均方误差的减小与信噪比近似为对数关系，而且在信噪比较低时EBPSK调制方式对目标不同频率散射系数估计的性能明显优于BPSK调制的估计性能，体现了基于CS的多载波雷达中EBPSK调制的优势.

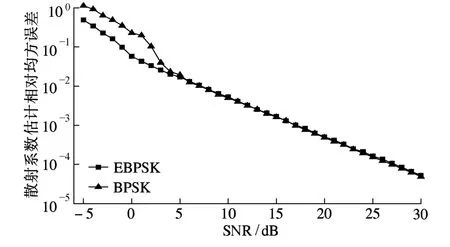
图7 EBPSK与BPSK调制目标散射系数估计性能对比

3 结语

本文给出了CS在多载波脉冲雷达中的应用仿真，在不同目标数条件下对比了 EBPSK与BPSK目标时延和多普勒频率的估计性能.结果表明基于CS的EBPSK多载波脉冲编码雷达的目标检测性能优于BPSK调制的目标检测性能.基于CS密集MCPC雷达的目标时延和多普勒频率估计性能优于正交MCPC雷达，而且EBPSK调制的密集多载波目标检测性能与BPSK调制基本相同，在有些条件下甚至更优.同时给出了不同压缩比下目标时延和多普勒频率估计的性能，指出在压缩比以及算法复杂度上的权衡关系.最后考虑了目标在不同频率下的散射系数估计问题，从仿真结果可知散射系数估计性能与信噪比呈对数关系，而且在低信噪比条件下EPBSK的目标散射系数估计性能优于BPSK的估计性能.

［1］Shen F F，Zhao G H，Shi G M，et al.Compressed sensing based ultra-wideband radar system［C］//IEEE CIE International Conference on Radar.Chengdu，China，2011，2:1850-1853.

［2］Baraniuk R G，Cevher V，Duarte M F，et al.Modelbased compressive sensing［J］.IEEE Transactions on Information Theory，2010，56(4):1982-2001.

［3］Sen S，Nehorai A.Sparsity-based multi-target tracking using OFDM radar［J］.IEEE Transactions on Signal Processing，2011，59(4):1902-1906.

［4］Herman M，Strohmer T.Compressed sensing radar［C］//IEEE Radar Conference.Rome，Italy，2008:1-6.

［5］刘俞伯.压缩感知在脉冲超宽带穿墙雷达中的应用［J］.大众科技，2012(5):47-49.

Liu Yubo.The application of CS in UWB through-wall radar［J］.Popular Science and Technology，2012(5):47-49.(in Chinese)

［6］Herman M A，Strohmer T.High-resolution radar via compressed sensing［J］.IEEE Transactions on Signal Processing，2009，57(6):2275-2284.

［7］王海青，张劲东，李彧晟，等.多载波雷达的单次回波速度估计方法［J］.电子与信息学报，2010，32(12):2868-2872.

Wang Haiqing，Zhang Jindong，Li Yusheng，et al.Multicarrier radar velocity measurement using single pulse［J］.Journal of Electronics and Information Technology，2010，32(12):2868-2872.(in Chinese)

［8］Berger C R，Wang Z H，Huang J Z，et al.Application of compressive sensing to sparse channel estimation［J］.IEEE Communications Magazine，2010，48(11):164-174.

［9］Eldar Y C，Mishali M.Robust recovery of signals from a structured union of subspaces［J］.IEEE Transactions on Information Theory，2009，55(11):5302-5316.

［10］Eldar Y C，Bolcskei H.Block-sparsity:coherence and efficient recovery［C］//IEEE International Conference on Acoustics，Speech and Signal Processing.Taipei，China，2009:2885-2888.

［11］Eldar Y C，Kuppinger P，Bolcskei H.Block-sparse signals:uncertainty relations and efficient recovery［J］.IEEE Transactions on Signal Processing，2010，58(6):3042-3054.

［12］Wu L N，Feng M，Qi C H，et al.Recent patents on ultra narrow band modulations［J］.Recent Patents on Signal Processing，2011，1(1):36-47.

［13］Feng M，Qi C H，Wu L N.Analysis and optimization of power spectrum on EBPSK modulation in throughput-efficient wireless system［J］.Journal of Southeast University:English Edition，2008，24(2):143-148.

［14］张士凯，吴乐南.EBPSK调制波的正交性及功率谱分析［J］.应用科学学报，2008，26(2):127-131.

Zhang Shikai，Wu Lenan.Orthogonality and power spectra of EBPSK modulated waves［J］.Journal of Application Sciences—Electronics and Information Engineering，2008，26(2):127-131.(in Chinese)

Compressive sensing for multi-carrier EBPSK radar

Chen Peng Wu Lenan

(School of Information Science and Engineering，Southeast University，Nanjing 210096，China)

Abstract:Compressive sensing(CS)technique is used in the multi-carrier phase-coded(MCPC)pulse radar，and the radar performance including the delay and Doppler frequency estimation and target scattering coefficients of different frequencies is analyzed.The extended binary phase shift keying(EBPSK)and binary phase shift keying(BPSK)performance of delay and Doppler frequency estimation are compared under the conditions of different numbers of targets using the block compressive sampling matching pursuit(BCoSaMP)reconstruction algorithm.And the target scattering coefficients of this radar are estimated.Simulation results show that the detection performance of the dense multi-carrier radar based on CS is better than that of the orthogonal multi-carrier radar，and under the condition of the orthogonal and the dense multi-carrier，the target detection performance of the EBPSK modulation outperforms that of the BPSK modulation.Furthermore，the estimation accuracy of the target scattering coefficients has a logarithmic relationship with signal to noise ratio(SNR)，and the EBPSK modulation signal has better target scattering coefficients estimation performance than the BPSK modulation signal at low SNR.Theoretical analysis and simulation results show the effectiveness and feasibility of the CS technique in terms of reducing the sampling frequency of the signal.

Key words:multi-carrier radar;compressive sensing;extended binary phase shift keying(EBPSK);target detection;block compressive sampling matching pursuit(BCoSaMP)

中图分类号:TN957.51

A

1001－0505(2014)01-0023-05

doi:10.3969/j.issn.1001 －0505.2014.01.005

收稿日期:2013-07-07.

陈鹏(1989—)，男，博士生;吴乐南(联系人)，男，博士，教授，博士生导师，wuln@seu.edu.cn.

基金项目:国家自然科学基金资助项目(61271204).

陈鹏，吴乐南.压缩感知在多载波EBPSK雷达中的应用［J］.东南大学学报:自然科学版，2014，44(1):23-27.［doi:10.3969/j.issn.1001 －0505.2014.01.005］