有色噪声背景下的水声跳频信号参数估计

姚 帅 方世良 王晓燕

(东南大学水声信号处理教育部重点实验室，南京 210096)

有色噪声背景下的水声跳频信号参数估计

姚 帅 方世良 王晓燕

(东南大学水声信号处理教育部重点实验室，南京 210096)

摘 要:针对现有跳频信号参数估计方法未考虑有色噪声的影响，且估计精度与速度难以兼得的问题，提出了一种有色噪声背景下的水声跳频信号参数估计方法.该方法首先根据水声信号有色噪声背景的特点，对有色噪声进行白化处理;然后，在详细推导分析跳频信号短时傅里叶变换时频脊线的特征的基础上，给出了跳频信号跳周期和起跳时间的估计方法;最后，基于估计得到的跳周期和起跳时间，进一步估计跳频频率.理论分析和仿真结果表明，该方法计算量小，工程实用性强，在有色噪声背景下可以实现跳频信号参数的快速稳健估计.

关键词:有色噪声;短时傅里叶变换;时频脊线;峰均功率比;跳频信号

跳频技术具有良好的抗干扰性、低截获概率和抗多径能力，已广泛应用于军事和民用通信中，近年来也开始应用于水下某些对通信保密、可靠性要求较高的场合［1-2］.受水声信道的复杂性、时变性以及自身载体平台辐射噪声的影响，水声跳频信号的背景噪声是有色的［3］.在有色噪声背景条件下，实现水声跳频信号参数的快速、高精度估计是最终达到水声对抗和侦察干扰目的的前提.

当前对跳频信号的参数估计大多采用时频分析的方法，时频分析方法通常分为线性和非线性两大类［4］.Wigner-Ville 分布(Wigner-Ville distribution，WVD)是典型的非线性时频分布［5-6］，具有理论上最高的时频分辨率，然而对于跳频信号这类多分量信号，WVD存在严重的交叉项干扰，使其应用受到限制.为了克服WVD交叉项的干扰，出现了大量的基于WVD改进的跳频信号参数估计算法.如文献［7］提出了一种采用平滑伪 WVD(smoothed pseudo WVD，SPWVD)的方法来估计跳频信号的参数，该方法能够有效地抑制交叉干扰项，但SPWVD对噪声敏感，在低信噪比(SNR)下参数估计性能急剧下降，且计算量十分巨大.文献［8-9］分别将SPWVD与快速折叠算法和小波变换相结合，这2个方法只是对跳频信号跳周期的估计方法进行了改进，与文献［7］的方法无本质区别.文献［10］提出了基于SPW 时频分析来估计跳频信号参数的方法，SPW与 SPWVD相比在计算量上占一定的优势，但在低SNR下，估计精度大大下降.文献［11］提出了基于重排SPWVD的参数估计方法，该方法提高了时频分布的聚焦性，但计算量大大增加.文献［12］将WVD与带通滤波器相结合，该方法能有效抑制跳频信号的交叉项干扰，但在低SNR下，带通滤波器的设计十分困难.上述基于WVD的方法，仅利用了时频脊线峰值频率或峰值频率能量特征中的一个，受噪声影响大，为了提高参数估计精度，需要增加大量的计算量，且均未考虑有色噪声，不适用于要求快速实现有色噪声背景下水声跳频信号参数估计的场合.

STFT在线性时频分布中应用最为广泛，其对噪声敏感度低、计算简单、运算量小，适用于要求快速实现跳频信号参数高精度估计的场合，因此本文采用基于STFT的跳频信号参数估计方法.该方法首先对水声跳频信号有色噪声进行白化处理;然后，提取STFT每段短时窗内白化后的功率谱的峰值频率并计算峰均功率比，利用跳频信号时频脊线在每一跳的起始时刻周期性地同时出现峰均功率比极小和频率瞬变的特征，使用 α-修正均值(α-TM)算法估计跳周期和起跳时间;最后，基于估计得到的跳周期和起跳时间，取各跳信号分别做FFT，并利用 Rife插值算法［13-14］修正有限长 FFT频谱泄露对频率估计的影响.此外，对算法的参数估计性能及运算复杂度进行了评估分析，并与文献［9］提出的参数估计方法进行了比较.

1 基于STFT时频脊线特征的跳频信号参数估计

1.1 有色噪声背景的预白化

跳频信号的离散模型为

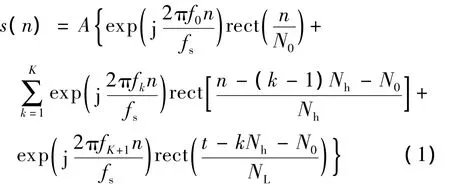
式中，A为信号幅度;rect(n/N0)为长度是N0的矩形窗;fs为采样频率;fk(k=0，1，2，…，K+1)为跳频频率;N0为起跳时间;Nh为跳周期;NL为末尾的非完整跳在观测时段内的持续时间.总观测长度为N=N0+KNh+NL，其中，N0，Nh和f0，fk，fK+1为待估计参数.含有色噪声的离散水声跳频信号模型为

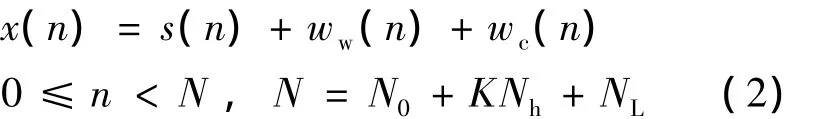
式中，ww(n)为高斯白噪声;wc(n)为水声载体平台产生的有色噪声，主要集中于低频段，该噪声可以用Esc型噪声的理论模型描述，其单边功率谱密度函数为［3］

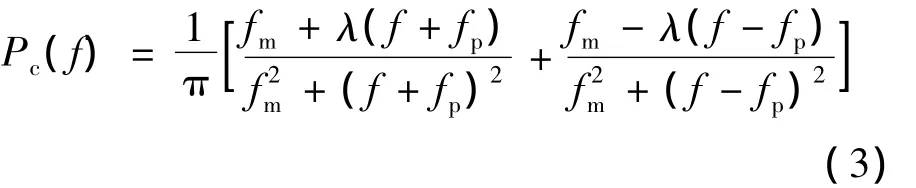
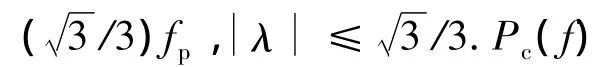
本文提出一种局部信噪比的方法对该有色噪声进行白化，局部信噪比的定义为

图1 有色噪声功率谱

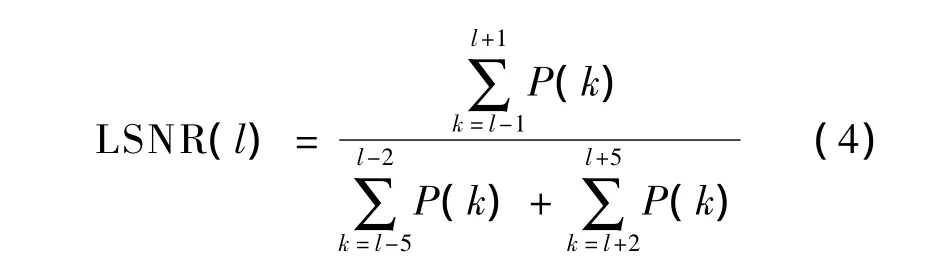
式中，P(k)为x(n)的离散功率谱密度.经过由式(4)定义的局部信噪比对接收信号的功率谱进行处理后，有色噪声功率谱被拉平，信号与白噪声的功率谱保持不变，如图2所示.白化后的离散信号x(n)可近似表示为

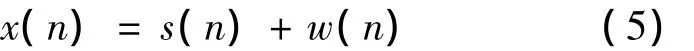
式中，w(n)为均值为0，方差为σ2的高斯白噪声.

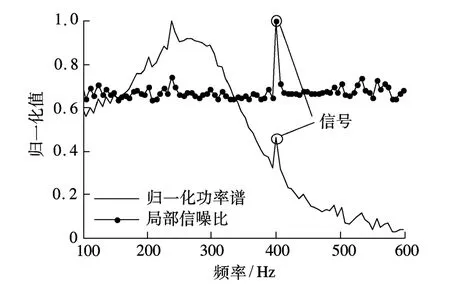
图2 有色噪声白化示意图

1.2 跳频信号STFT时频脊线特征

经过白化处理后的x(n)的离散STFT为

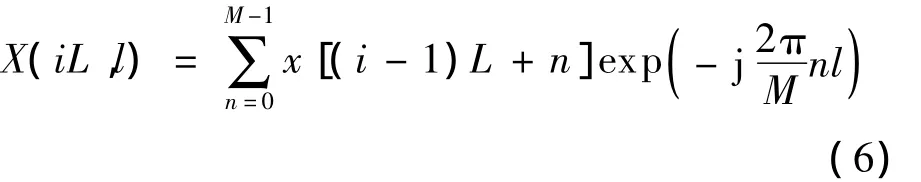
式中，l=0，1，2，…，M－1;i=1，2，…，I;L为短时窗的移动步进;M为短时窗长;I=「N/L」为观测时间内短时窗的总个数.式(6)可通过FFT实现，从而提高方法的计算效率.设STFT第i段短时窗内包含长度为Mk(0≤Mk≤M)的第k跳和长度为M－Mk的第k+1跳信号，如图3所示.记该段观测信号为

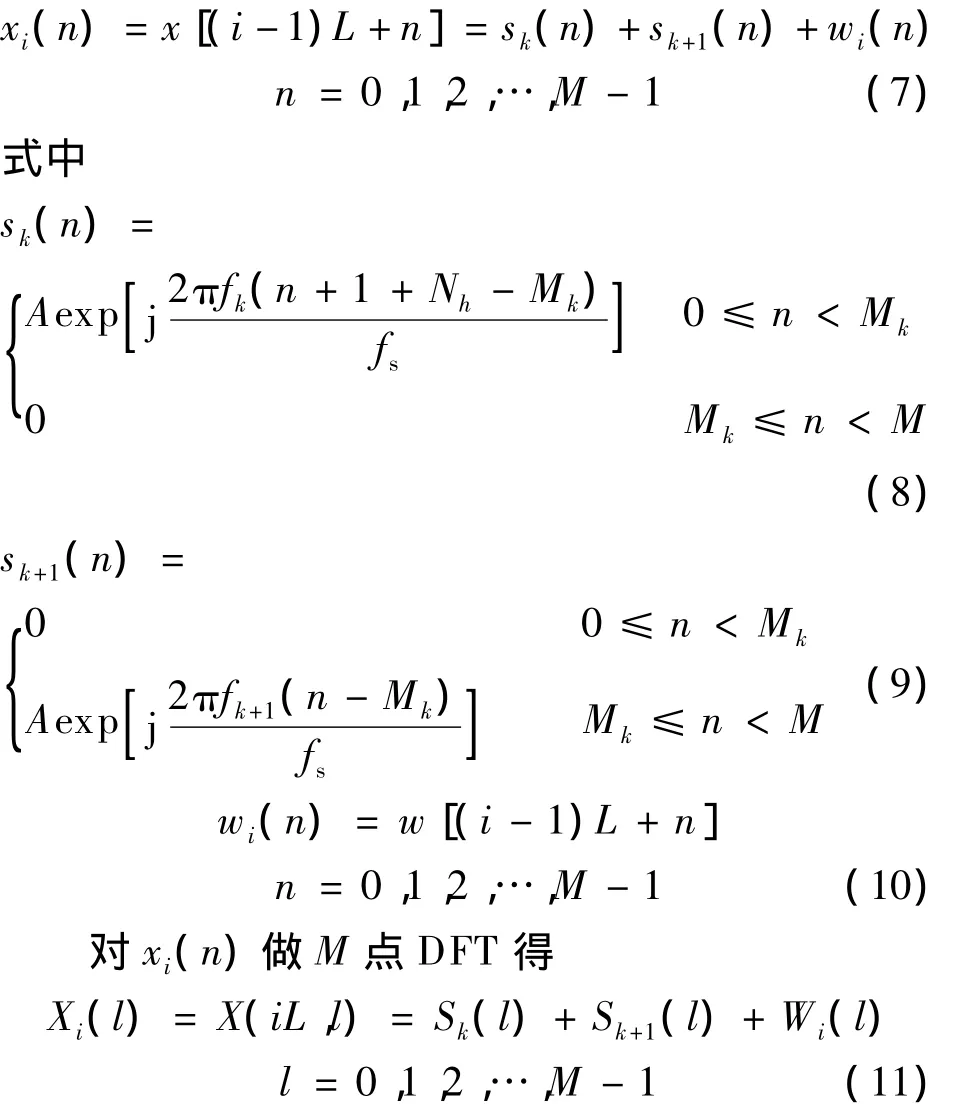
式中，Sk(l)，Sk+1(l)和Wi(l)分别为sk(n)，sk+1(n)和wi(n)的M点DFT.Wi(l)只在统计意义上成立，对每个离散频率l，Wi(l)均为随机变量，因此W(l)为随机序列.由式(11)可得xi(n)的功率谱密度为

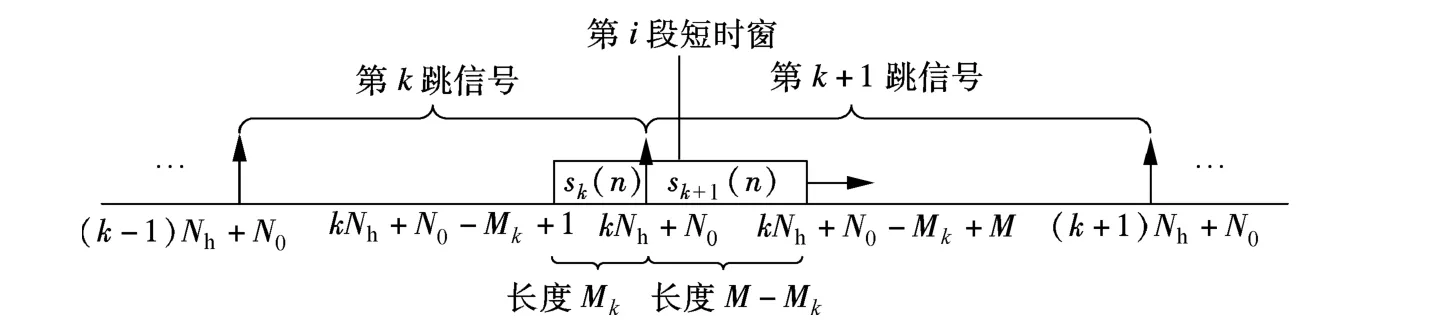
图3 跳频信号移动短时窗进行STFT的示意图

式中，real［·］为取实部运算.式(12)中的第4项为跳频信号的第k跳和第k+1跳的交叉项，由于跳频信号的不同跳信号是相互正交的，因此该项可以忽略;最后2项为跳信号与噪声的交叉项，由于噪声和信号是相互独立的，最后2项也可忽略.因此有

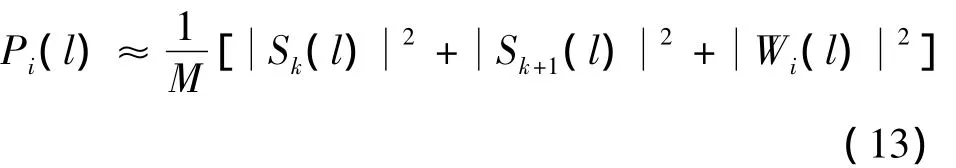
定义第i段短时窗时频脊线的峰均功率比为

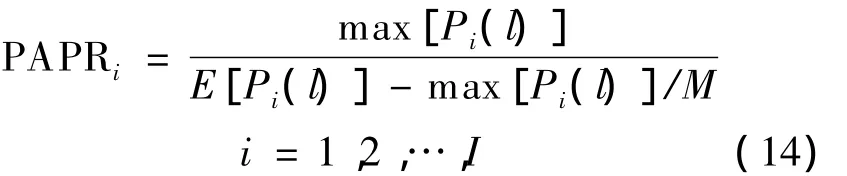
式中，E［·］表示数学期望;max［·］表示取最大值运算.下面分析式(13)中各项的取值，以求解式(14).

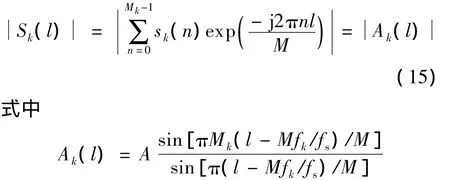
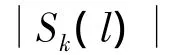
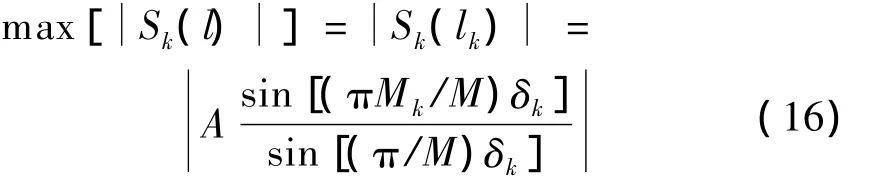
式中，δk=Mfk/fs－lk，当M较大时近似可得

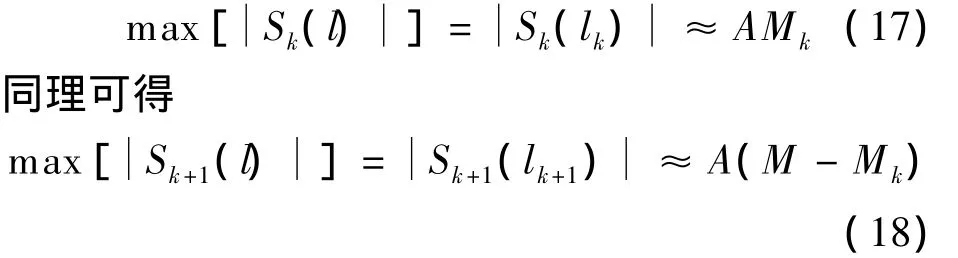
在较高SNR条件下，将式(17)和式(18)代入式(13)得

由于wi(n)是均值为0，方差为σ2的高斯白噪声，因此Wi(l)也服从高斯分布，其均值和方差分别为

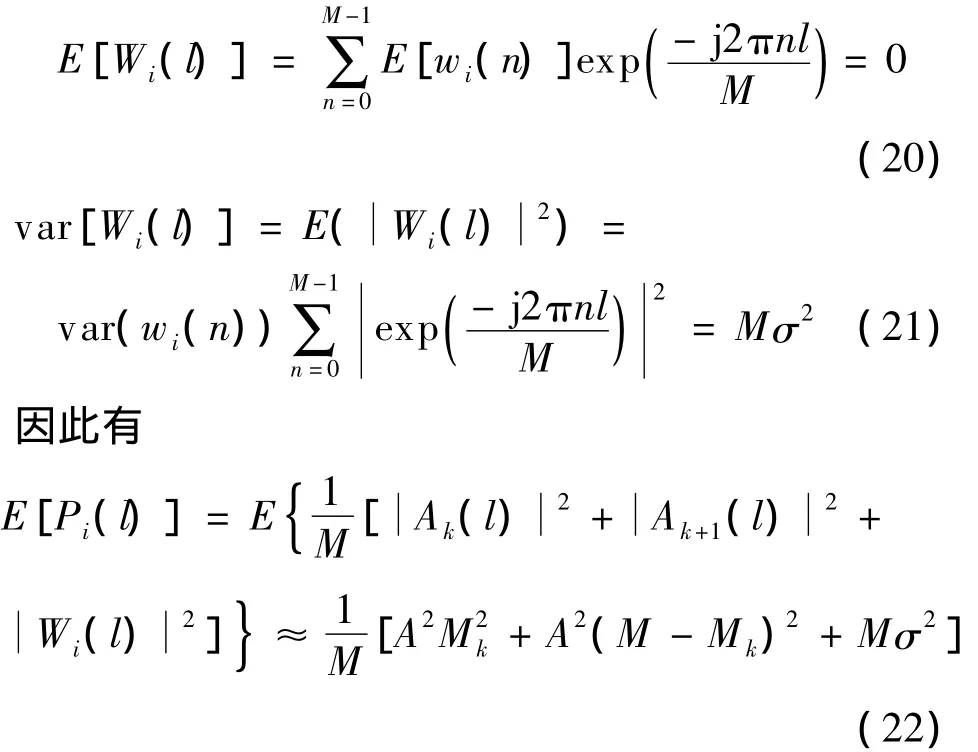
将式(19)和式(22)代入式(14)得

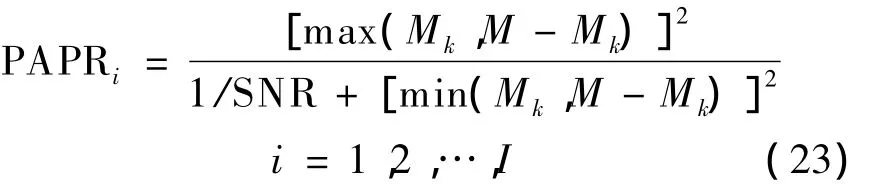
式中，SNR=A2/σ2;min(·)表示取最小值运算.由式(23)可得，当Mk=M/2时，即第i段短时窗的中心处于第k+1跳信号的起始时刻(对应于图3中的kNh+N0点)时，PAPRi取得极小值，即

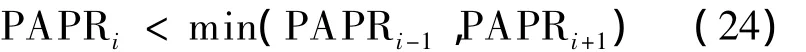
设Pi(l)的最大线谱对应的l记为li，其对应的峰值频率为，则由式(19)可得，当Mk=M/2时，有li－1=lk，li+1=lk+1.而索引lk和lk+1分别对应于第k跳和第k+1跳信号的跳频频率估计值，即第i－1段和第i+1段短时窗的峰值频率有瞬变现象.

综上所述，跳频信号的STFT时频脊线表现出如下特征:在跳频信号每一跳的起始时刻周期性地同时出现峰均功率比极小和频率瞬变的特征.利用这一瞬变特征，可初步估计得到跳频信号的每一跳的起始时刻为

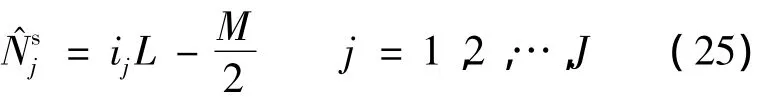
式中，J为满足时频脊线特征的总点数.

1.3 参数估计方法

首先，对做差值得(对应于各跳信号的起始时刻的时间差，即跳周期).当SNR较低时，受噪声影响，估计得到的中会存在异常值.因此，直接对求均值估计跳周期稳健性较差，本文采用对异常值敏感度较低的α-TM算法.跳周期Nh的α-TM估计值为

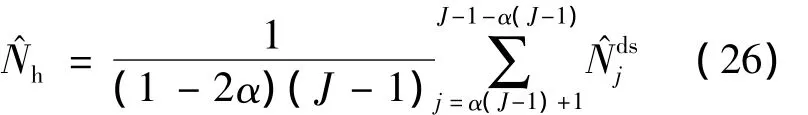
式中，为排序后的结果.估计得到后，可以用对每一跳的起始时刻进行异常值修正，修正的基本思想为:将对应于点剔除，在对应于的点后插入点.利用上述方法修正后的每一跳的起始时刻序列记为，其中J'为修正后的总点数，同样利用α-TM算法估计跳频信号的起跳时间，即

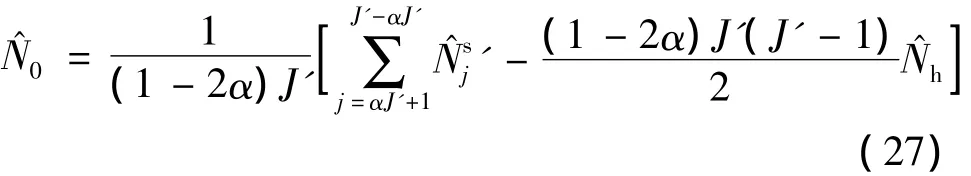
由和可进一步得到观测时间内的跳频数和每一跳所占的离散时间范围(非负整数)，分别为

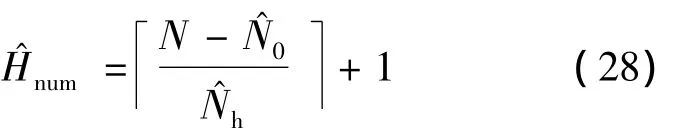
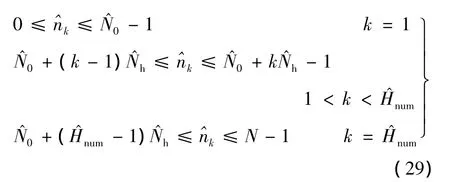
式中，「·」为向上取整运算.最后根据估计得到的k，取每一跳信号重新进行FFT，以估计各跳信号的频率.由式(19)可知，只要估计的各跳的时间范围k占实际各跳信号的主要部分，即可较为准确地估计出每一跳信号的频率.由于每一跳信号所占的时间长度是有限的，因此直接利用FFT最大线谱法估计信号频率时，不可避免地存在频谱泄露，本文采用Rife插值算法对频谱泄露进行修正.设第k跳信号的幅度谱为最大线谱所对应的索引值为lk，则Rife插值公式为

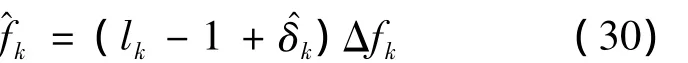
式中，Δfk=fs/Lk，Lk为所对应的离散采样点数;的表达式为

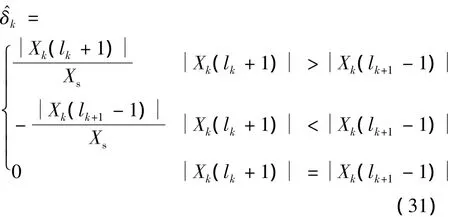
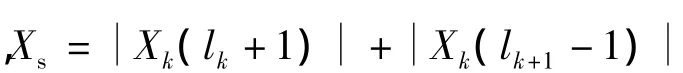
2 算法性能分析

2.1 仿真分析

为了验证本文提出的跳频信号参数盲估计方法的性能，根据式(1)和(2)的跳频信号和观测信号模型，仿真产生一段跳频信号.跳频信号参数为:采样频率fs=2.4 kHz，观测时间内包含8跳信号，其中包含K=6个完整跳周期，2个非完整跳周期，跳周期Nh对应的采样点长度为600，起跳时间N0对应的采样点长度为400，末尾的非完整跳长度NL为300个采样点，总观测长度N为4 300个采样点，跳频频率分别为 400，360，420，340，380，300，320，440 Hz;有色噪声参数fm=115.47 Hz，fp=300 Hz，λ=0.577;白噪声SNR=10lg(A2/σ2)，由－6 dB以步进为3 dB增加到12 dB.对于每一个SNR，各进行1 000次Monte Carlo试验.将本文方法与文献［9］提出的方法(同样利用时频脊线，且整体性能优于现有的跳频参数估计方法)进行比较.仿真分析中，STFT的窗长M取为256个采样点，步进L取为窗长的1/4，因此L对应的采样点长度为64.α-TM 算法中取 α=0.25.

统计跳周期和起跳时间的估计均方误差(MSE)，其定义为

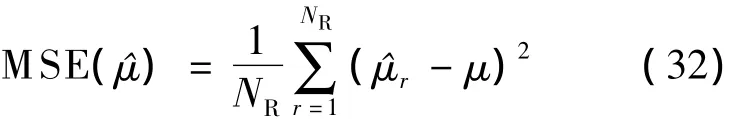
式中，为参数估计值;μ为参数真实值;NR为Monte Carlo试验次数，这里NR=1 000.对于跳频频率，由于观测时间内有多个跳频频率，为便于分析，统计跳频频率的平均均方误差(mean MSE，MMSE):

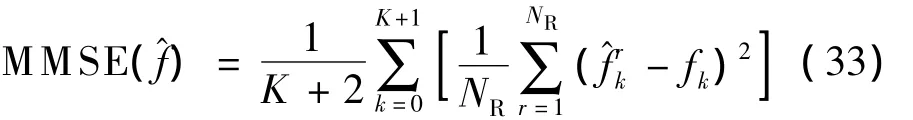
式中为第r次Monte Carlo试验中第k跳信号的频率估计值.

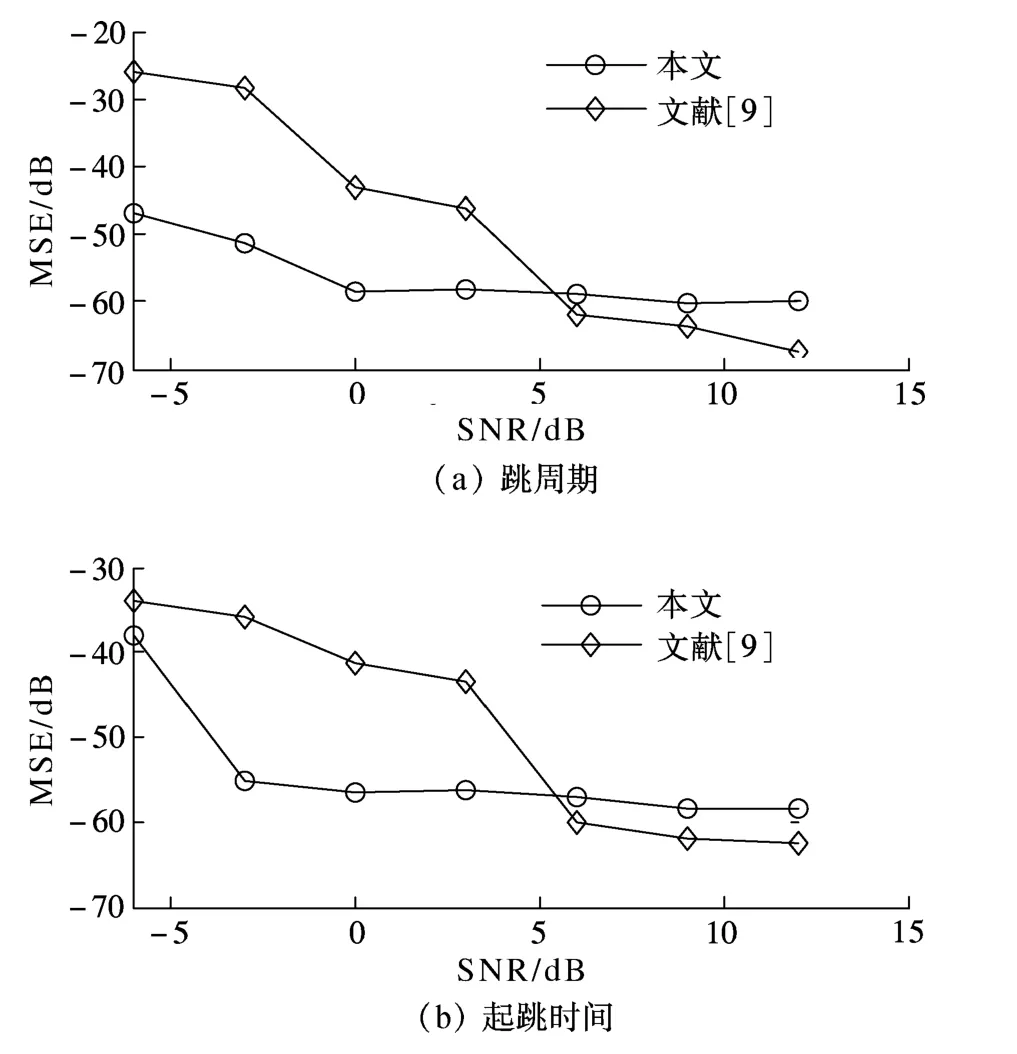
图4 跳周期和起跳时间的估计均方误差

跳周期和起跳时间的估计均方误差随SNR的变化曲线如图4所示.由图可见，当SNR＜6 dB时，本文方法的跳周期和起跳时间估计均方误差小于文献［9］的方法;而当SNR≥6 dB时，本文方法的估计均方误差大于文献［9］.这是由于低SNR下，影响跳周期和起跳时间参数估计精度的主要因素是随机噪声所带来的随机误差，而STFT提取信号的脊线频率及其能量对噪声的敏感度低于文献［9］中基于 SPWVD 的方法［15-16］，且本文方法同时利用了跳频信号时频分布的峰值频率和峰值频率能量(对应于峰均功率比)特征，而文献［9］仅利用了峰值频率能量特征，因此在低SNR下，本文方法稳健性更强;而当SNR较高时，影响跳周期和起跳时间参数估计精度的主要因素是方法的时间分辨率，本文方法的时间分辨率取决于STFT的窗长，远小于文献［9］方法的时间分辨率，因此在高SNR条件下，文献［9］方法的跳周期和起跳时间的估计精度更高.

跳频频率的平均均方误差随SNR的变化曲线如图5所示.由图可看出，当SNR＞-6 dB时，本文方法估计的跳频频率平均均方误差远小于文献［9］的方法.这是由于文献［9］中直接取估计得到的各跳周期时间中点的脊线频率作为该跳信号频率的估计值，而本文方法对各段跳频信号重新做FFT.这样处理的优势在于:① 只要估计得到的各跳的时间范围占实际各跳信号的主要部分，重新做FFT可有效克服跳周期和起跳时间估计误差所带来的影响;②采用了Rife插值算法能够有效降低有限长FFT方法的频谱泄露的影响.这与第1节的理论分析相一致，因此，本文方法跳频频率估计精度高于文献［9］的方法.

图5 跳频频率平均均方误差

2.2 运算复杂度分析

记一次M点的FFT运算量为ωM，本文方法的运算量为ΩSTFT，文献［9］方法的运算量为ΩSPWVD.这里仅统计占运算量主要部分的处理过程的计算量，而忽略部分实际处理过程.本文方法的主要处理过程包括跳频信号STFT的计算和跳频频率的估计，因此本文方法的总运算量为

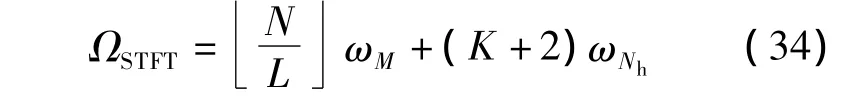
文献［9］方法的主要处理过程包括N点Hilbert变换，N点SPWVD和N点峰值频率能量的一维小波变换，其中N点Hilbert变换包括一次N点FFT和一次N点IFFT，每一采样时刻点SPWVD需要做N点FFT，因此计算量为

做一次M点FFT需要(Mlog2M)/2复数乘和Mlog2M复数加，为便于比较，将运算量由复数乘和复数加的次数表示.将本文的仿真参数N=4 300，M=256，L=64，K=6和Nh=600分别代入式(34)和(35)，其计算结果如表1所示.由表可知，本文方法的计算量远小于文献［9］的方法.相比文献［9］的方法，本文方法更适用于需要实现跳频信号参数快速估计的场合.

表1 本文方法与文献［9］方法计算量比较 次

3 结语

本文通过对跳频信号STFT时频脊线的峰均功率比和瞬时频率特征的分析，提出了一种有色噪声背景下，基于STFT时频脊线特征的水声跳频信号参数估计方法.理论分析和仿真结果表明，该方法可以在有色噪声背景和较低的信噪比下，以很小的计算量实现跳频信号参数的高精度估计.本文方法整体性能优于文献［9］的方法，能够较好地适用于非合作情况下跳频信号参数的快速高精度估计的应用场合，具有较高的工程实用价值.

［1］Lv S，Shen X H.Research on shallow water acoustic communication based on frequency hopping［C］//IEEE International Conference on Signal Processing，Communication and Computing.Hong Kong，China，2012:392-395.

［2］Yue L，Yang X，Wang M，et al.Performance of turbo coded FH/MFSK in shallow water acoustic channel［C］//IEEE11th International Conference on Signal Processing.Beijing，China，2012:1401-1405.

［3］陶笃纯.按辐射噪声平均功率谱形状识别船舶目标［J］.声学学报，1981(4):218-228.

Tao Duchun.Recognizing ship objects by the shape of averaged power spectrum of radiated noise［J］.Acta Acoustic，1981(4):218-228.(in Chinese)

［4］Hlawatsch F，Boundreaux-Bartels G F.Linear and quadratic time-frequency signal representations ［J］.IEEE Signal Processing Magazine，1992，9(2):21-67.

［5］Thomas M，Lethakumary B，Jacob R.Performance comparison of multi-component signals using WVD and Cohen's class variants［C］//IEEE2012InternationalConference on Computing，Electronics and Electrical Technologies.Tamil Nadu，India，2012:717-722.

［6］Thomas M，Jacob R，Lethakumary B.Comparison of WVD based time-frequency distributions［C］//2012International Conference on Power，Signals，Controls and Computation.Thrissur，Kerala，India，2012:1-8.

［7］赵俊，张朝阳，赖利峰，等.一种基于时频分析的跳频信号参数盲估计方法［J］.电路与系统学报，2003，8(3):46-50.

Zhao Jun，Zhang Zhaoyang，Lai Lifeng，et al.Blind parameter estimation of frequency-hopping signals based on time-frequency analysis［J］.Journal of Circuits and Systems，2003，8(3):46-50.(in Chinese)

［8］王国华，俞能海.基于快速折叠算法和时频分析的LPI跳频信号截获［J］.电子与信息学报，2007，29(7):1569-1572.

Wang Guohua，Yu Nenghai.FFA and TFA-based interception of LPI frequency hopping signal［J］.Journal of Electronics and Information Technology，2007，29(7):1569-1572.(in Chinese)

［9］冯涛，袁超伟.基于时频脊线的跳频参数盲估计［J］.电子学报，2011，39(12):2921-2925.

Feng Tao，Yuan Chaowei.Blind parameter estimation of frequency-hopping signals based on the time-frequency distribution maxima［J］.ACTA Electronica Sinica，2011，39(12):2921-2925.(in Chinese)

［10］郭艺，张尔扬，沈荣骏.跳频信号时-频域分析与参数盲估计方法［J］.信号处理，2007，23(2):210-213.

Guo Yi，Zhang Eryang，Shen Rongjun.The time-frequency analysis and blind parameter estimation of frequency hopping signals［J］.Signal Processing，2007，

http://journal.seu.edu.cn 23(2):210-213.(in Chinese)

［11］Chen T C.Joint signal parameter estimation of frequency-hopping communications［J］.Communications，IET，2012，6(4):381-389.

［12］冯涛，袁超伟.跳频信号的时频分析新方法［J］.北京邮电大学学报，2010，33(3):10-14.

Feng Tao，Yuan Chaowei.A method of time-frequency analysis for frequency-hopping signals［J］.Journal of Beijing University of Posts and Telecommunications，2010，33(3):10-14.(in Chinese)

［13］姚帅，方世良，王晓燕.联合STFT-迭代变权拟合的LFM 信号参数估计方法［J］.信号处理，2012，28(10):1408-1415.

Yao Shuai，Fang Shiliang，Wang Xiaoyan.Parameterestimation of LFM signal based on combined short time Fourier transform and iteratively reweighted fit［J］.Signal Processing，2012，28(10):1408-1415.(in Chinese)

［14］马阳阳，李京华，张燕荣.基于 FFT幅度和相位插值的频率估计改进算法［J］.计算机与数字工程，2012，40(8):39-41.

Ma Yangyang，Li Jinghua，Zhang Yanrong.An improved frequency estimation algorithm based on FFT phase and amplitude［J］.Computer and Digital Engineering，2012，40(8):39-41.(in Chinese)

［15］Djurovic I，Stankovic L.STFT-based estimator of polynomial phase signals［J］.Signal Processing，2012，92(11):2769-2774

［16］Pei S C，Huang S G.STFT with adaptive window width based on the chirp rate［J］.IEEE Transactions on Signal Processing，2012，60(8):4065-4080.

Parameter estimation of underwater acoustic frequency-hopping signals in colored noise

Yao Shuai Fang Shiliang Wang Xiaoyan

(Key Laboratory of Underwater Acoustic Signal Processing of Ministry of Education，Southeast University，Nanjing 210096，China)

Abstract:For the existing parameter estimation methods of the frequency-hopping(FH)signals，colored noise is without consideration and the estimation accuracy and speed are mutually exclusive.To solve these problems，a method is proposed for the parameter estimation of underwater acoustic FH signals in colored noise.The colored noise is first whitened according to the features of underwater acoustic colored noise.Then，based on detailed derivation and analysis for the characteristics of the short time Fourier transform time-frequency distribution maxima of the FH signals，methods for estimating the hop duration and hop timing are given.Finally，the hopping frequencies are estimated using the estimated hop duration and hop timing.The theoretical analysis and simulation results show that the proposed method has a small amount of computation amount and can be easily realized in practice.The parameters of underwater acoustic FH signals in colored noise can be estimated fast and robustly by the proposed method.

Key words:colored noise;short time Fourier transform(STFT);time-frequency distribution maxima;peak-to-average power ratio(PAPR);frequency-hopping signal

中图分类号:TN911.72

A

1001-0505(2014)01-0012-07

doi:10.3969/j.issn.1001-0505.2014.01.003

收稿日期:2013-07-23.

姚帅(1987—)，男，博士生;方世良(联系人)，男，博士，教授，博士生导师，slfang@seu.edu.cn.

基金项目:国家自然科学基金资助项目(11104141，11104029)、中央高校基本科研业务费专项资金资助项目(3204003301)、声纳技术国防科技重点实验室开放基金资助项目(KF201201).

姚帅，方世良，王晓燕.有色噪声背景下的水声跳频信号参数估计［J］.东南大学学报:自然科学版，2014，44(1):12-18.［doi:10.3969/j.issn.1001-0505.2014.01.003］