基于新型可逆门的可扩展可逆比较器

朱皖宁 陈汉武，2 阮 越

(1东南大学计算机科学与工程学院，南京 210096)(2东南大学计算机网络和信息集成教育部重点实验室，南京 210096)

基于新型可逆门的可扩展可逆比较器

朱皖宁1陈汉武1，2阮 越1

(1东南大学计算机科学与工程学院，南京 210096)
(2东南大学计算机网络和信息集成教育部重点实验室，南京 210096)

摘 要:针对当前可逆比较器设计方案缺乏可扩展性的问题，提出了基于新型可逆门的具有可扩展性的可逆比较器可逆逻辑电路设计方案.该方案根据二进制数比较的特点采用递归思想将电路分解为2种新型可逆门，对分解出的每一个可逆门进行可逆逻辑综合，再将这2种可逆门级联成可逆比较器.给出了设计方案中每一步的逻辑演算，利用编码的思想进行带无关项的可逆逻辑综合，最终给出了具体的可逆比较器的综合方案.同时，以可逆比较器作为元器件给出了败者树排序电路，将排序的时间复杂度降低到Θ(n).

关键词:可逆比较器;新型可逆门;递归

根据 Landauer［1］的研究，每个比特的信息量损失会造成至少KTln2焦耳的能量散发，其中K为 Boltzmann常量，K=1.380 650 5×10－23m2/(kg·s2·K)，T为绝对温度.信息量的损失是由于电路不可逆导致的.超大规模集成电路若继续采用不可逆电路设计，其芯片能量散发导致的片体发热将会限制其集成度进一步提高.

Barenco等［2］证明了必须使用可逆逻辑电路才能避免能量散发.因此在低能CMOS设计和纳米技术电路系统领域中可逆逻辑综合算法具有重要的研究意义.光计算和量子计算的电路模型也需要使用可逆逻辑电路.量子逻辑门都是酉变换，对应同一个数域上输入和输出的双射，所以量子逻辑门均可逆［3］.经典的可逆逻辑无法处理量子态的叠加，只能作为量子可逆逻辑电路的特例或者是量子可逆逻辑电路的一个子集.

自从1985年Peres发现了 Peres门后［4］，新型可逆门的研究成为热点之一.Khan［5］发现了 NG门，实现了经典的与或非操作.Thapliyal等［6］提出了TSG门，实现了单门的4量子线路全加，从而完成了多可逆门组合的可逆乘法器的设计.此后，HNG门、PFAG门等多种可逆逻辑门［7-10］的发现进一步降低了乘法器的开销.

Cheng等［11］提出了基于经典可逆比较器的量子归并排序算法电路，使归并排序算法的时间复杂度降低至Θ((logn)2)，并在此基础上提出基于排序的量子交换机，但未能给出可逆比较器具体的可逆逻辑电路描述.李明翠［12］提出了基于Toffoli门的可逆比较器综合方案，虽然此方案利用了模块化的思想，但并没有给出合并较小模块以获得较大模块的方法，并且合并后的CG可逆门电路仍然需要单独设计，因此该方案并不是一个可扩展的方案，在大规模集成电路设计中不能得到很好的应用.

为了构造具有可扩展性的任意n比特可逆比较器，本文使用递归的思想构建电路，利用编码的思路综合带无关项的可逆逻辑电路，从而大大简化了电路设计的复杂性，并且减少了方案的开销.并在可逆比较器的基础上，设计了经典的败者树排序算法的可逆逻辑电路，降低了败者树排序算法的时间复杂度.

1 CNT门库和EGT门

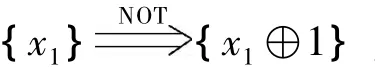
可控非门(CNOT门)是作用在2个比特上的可逆门，包含一个控制端c和一个受控端t.当c为真时，t发生翻转，反之则不做任何操作，即)

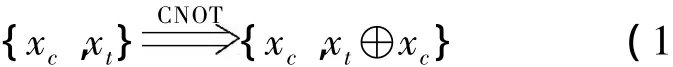
经典Toffoli门是作用在3个比特上的可逆门，包含2个控制端c1，c2和一个受控端t.当2个控制端c1和c2都为真时，t发生翻转，否则不做任何操作，即

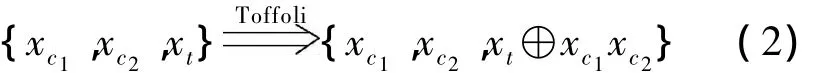
如图1所示的CNT门库包含了以上3个门.可以证明通过CNT门库能够生成所有经典的可逆逻辑电路.

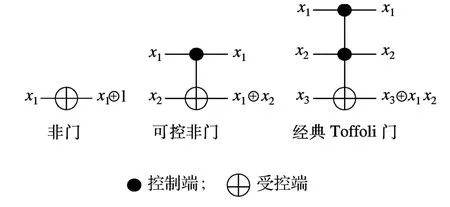
图1 CNT门库

当Toffoli门的控制端大于等于2个时，称为GT(general Toffoli)门.设GT门的控制端为{xc1，xc2，…，xci}，受控端为{xt}.如图 2(a)所示的 GT门，当控制端都为真时，受控端才发生翻转，否则不做任何操作.GT门的作用可用下式表示:

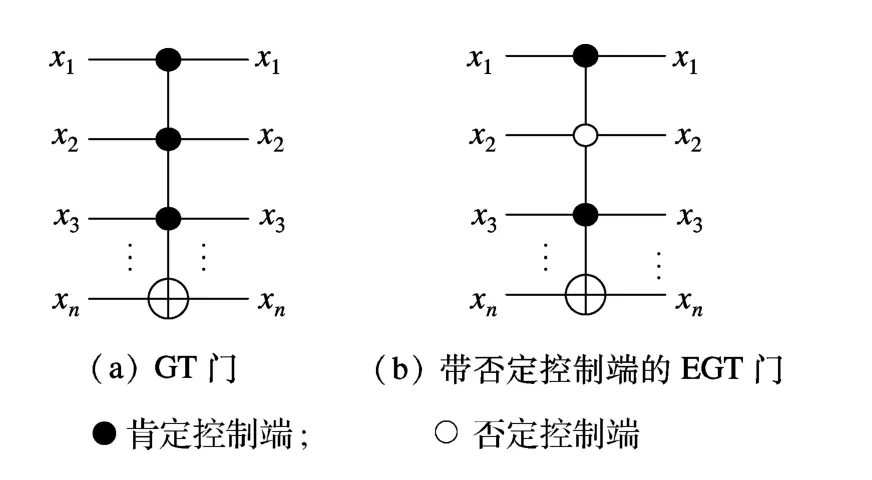
图2 EGT门

EGT(extend general Toffoli)门是在GT门的基础上，增加了控制端为假时受控端发生比特翻转的电路.为了区分2种控制端，称控制端为真时门生效的为肯定控制端，另外一种为否定控制端.设EGT 门的肯定控制端为{xc1，xc2，…，xci}，否定控制端为{xn1，xn2，…，xnk}，受控端为{xt}.EGT 门的作用可用下式表示:

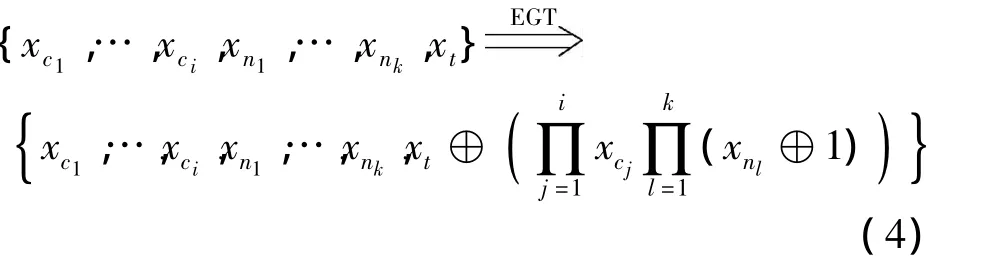
如图2(b)所示的EGT门，空心圈表示否定控制端，即当控制信号为0时，受控端翻转.当门的控制端数量较多时，开销很大，因此尽量使用控制端较少的门来综合电路.

2 可逆比较器的构造

设n位二进制数An=a1…an－1an，其中ai表示An中第i位的值，i∈{1，2，…，n}，ai∈{0，1}.类似地，定义n位二进制数Bn=b1…bn－1bn，若不满n位，则在高位补0.设An和Bn的比较结果为c=c1c2，则

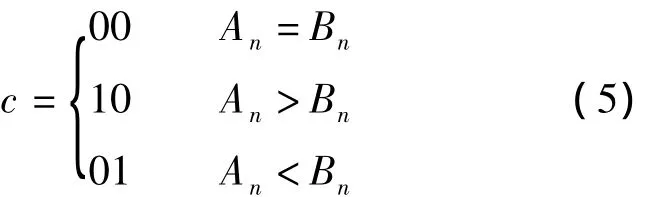
目前使用的可逆逻辑综合算法需要先求出电路的真值表，然后根据真值表求解，但该算法存在如下问题:①由于位数n是个变量，因此无法确定电路的真值表.② 由于根据真值表求解的电路不具备可扩展性，因此当n发生变化时，就必须重新构造真值表生成一个全新的电路.为了解决这2个问题，就不能从全局状态出发，而是需要将电路解构，用递归的方式进行分析.

2 个n位二进制数的比较是从高位开始按位比较，且第i－1位的比较结果会影响到第i位.设二元函数C(An，Bn)为2个n位二进制数的比较函数，实现该函数需要构造2个新的函数:① 比较2个1比特数大小的函数;② 根据高位情况进行综合比较的函数.设二元函数C0(a，b)为1比特数比较函数;二元函数C1(c'，C')为根据当前位和高位比较结果进行综合比较的函数，从而得到如下递归表达式:

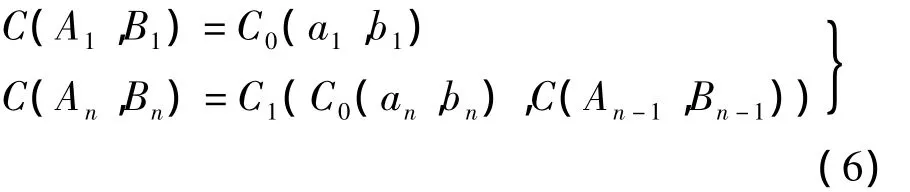
由式(6)可知，求解函数C就是求解函数C0和C1的可逆门电路，然后加以级联.

2.1 函数C0的可逆逻辑电路

对任意2个一位二进制数A1=a和B1=b的大小进行比较，存在如下4种可能:

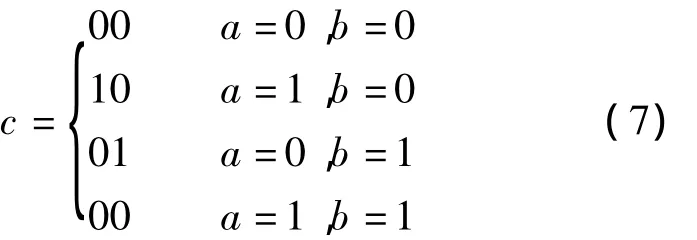
由式(7)可知，将c1和c2的初值赋为0，级联2个EGT门即可完成C0的可逆逻辑电路(见图3).为简便起见，下文将C0看作一个新的可逆门.

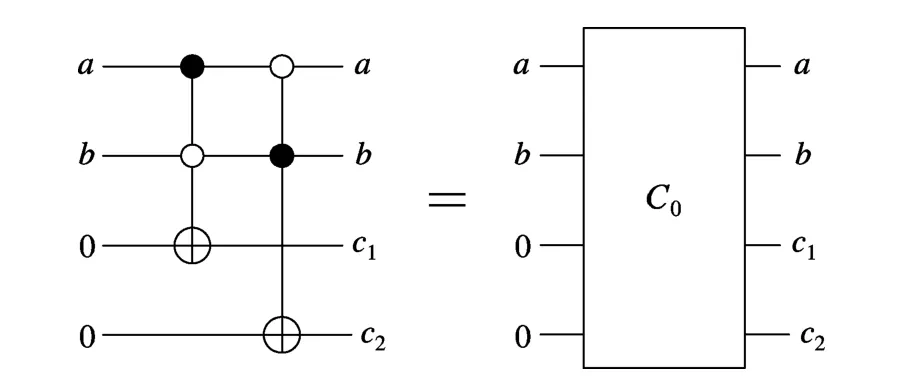
图3 C0的可逆逻辑电路

2.2 函数C1的可逆逻辑电路

求解函数C可逆逻辑电路的关键是设计C1可逆门电路.其设计过程可分为4个步骤:

①分析C1函数的功能

该函数的2个参数分别是当前位的比较结果和高位n－1位的比较结果.当高位不相等时函数值为高位比较结果，否则为当前位的比较结果.

② 确定C1(c'，C')的定义域和值域

由式(5)、(7)可知，c'∈{00，01，10}，C'∈{00，01，10}.因此函数C1(c'，C')的定义域为{00，01，10}.类似地，由于比较结果仅需要这3个二进制数即可确定，因此C1(c'，C')∈{00，01，10}.

③ 确定C1(c'，C')的映射方式

根据前文分析，当且仅当C'=00时，C1(c'，C')=c'，否则C1(c'，C')=C'.由此可得函数C1的映射方式为

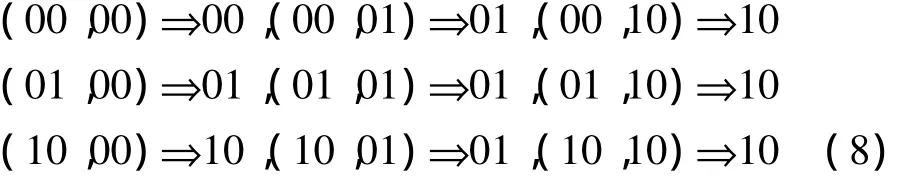
④由式(8)得到部分真值表

由式(8)可知，这是一个求解带无关项的可逆逻辑问题，即输出和输入不一一对应.因此在对应的可逆逻辑真值表中存在随机项.根据式(8)获得了C1的真值表，如表1所示，其中a'，b'是垃圾位，d'，e'表示函数的输出，a，b表示高位，d，e表示当前位.x可任意设置为0或者1，只要最后满足可逆即可.

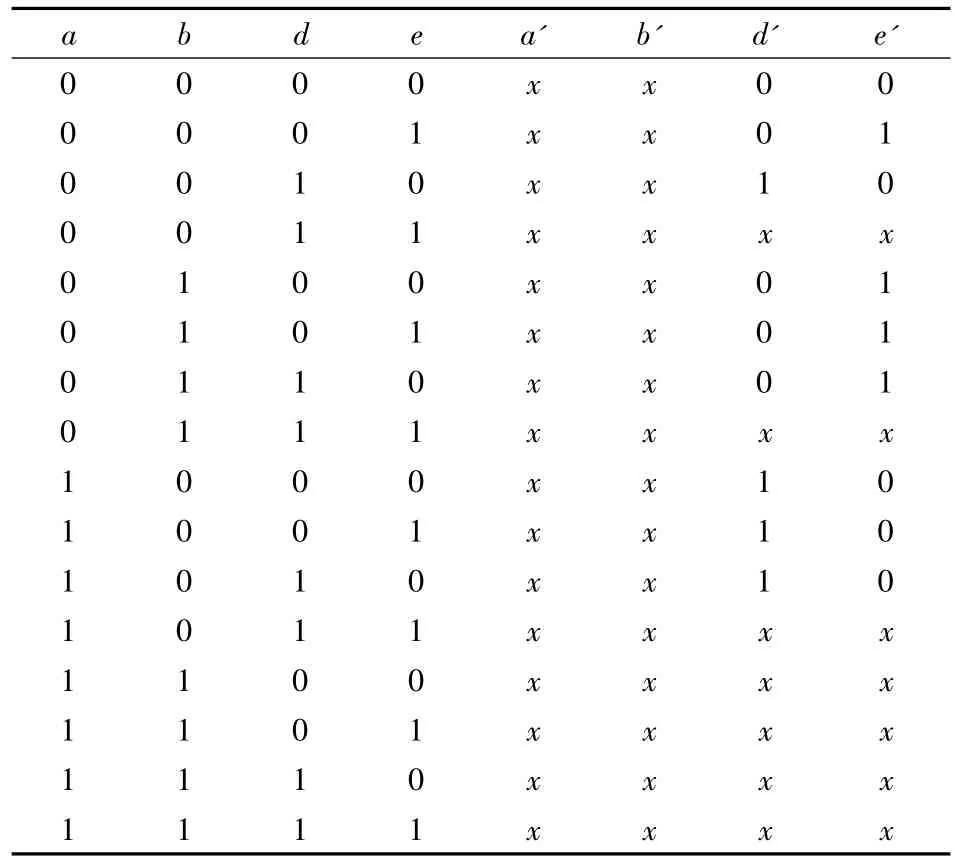
表1 C1的真值表

根据文献［13］，从不完整的真值表中可抽取出所需要的d'和e'的Reed-Muller展开式:

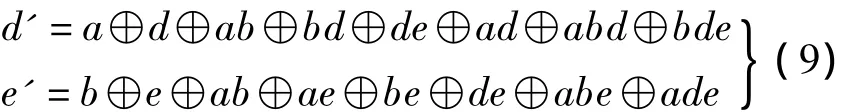
根据式(9)，利用Reed-Muller展开式可逆逻辑综合算法［14］，得到如图4所示的C1的可逆逻辑电路图.

从图4(a)可看出，实现该可逆逻辑电路所需要的门电路太多，并且还存在1个3控制端的EGT门，导致电路开销太大.在可逆比较器电路设计中，C1需要重复使用多次，若其开销太大，会导致整个电路的开销过大.因此本文提出利用编码的思想来构造C1电路，可以有效地降低电路开销.

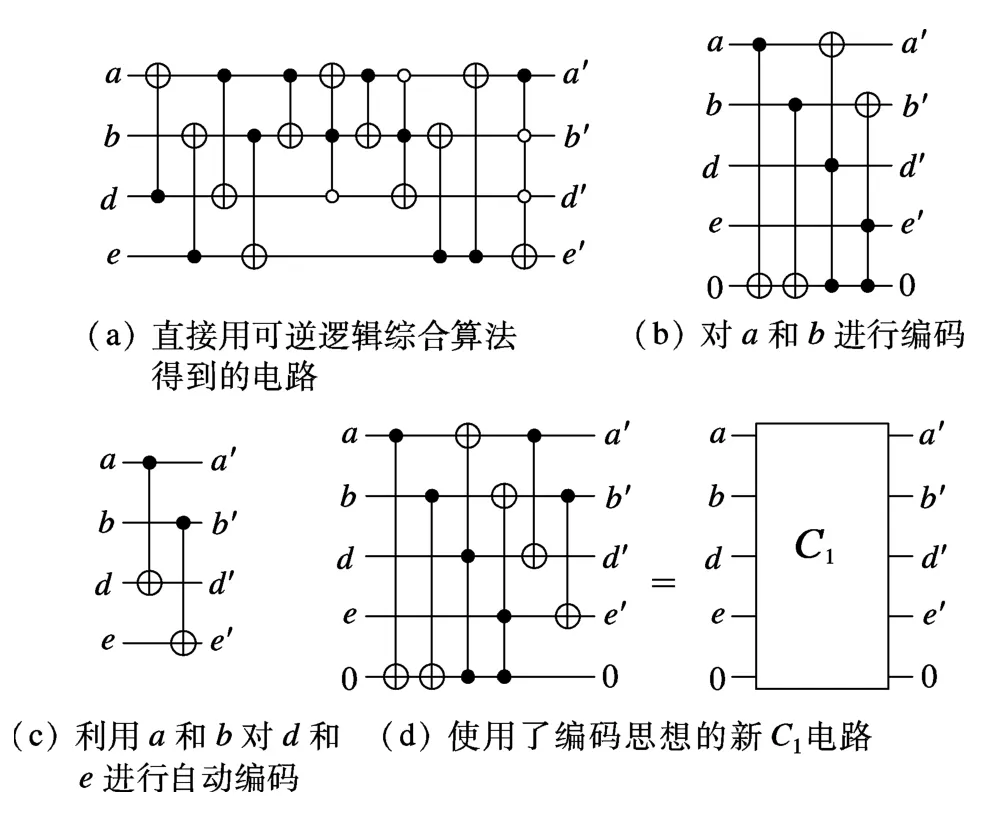
图4 C1的可逆逻辑电路图

从表1可看出，C1的函数值为d'和e'的值，因此可对整个电路进行编码操作.将a'和b'作为信号位，用a'和b'对d和e进行自动编码.在对a'和b'进行编码时，不能改变d和e，否则无法获得正确的解.设a'和b'的信号编码如下:

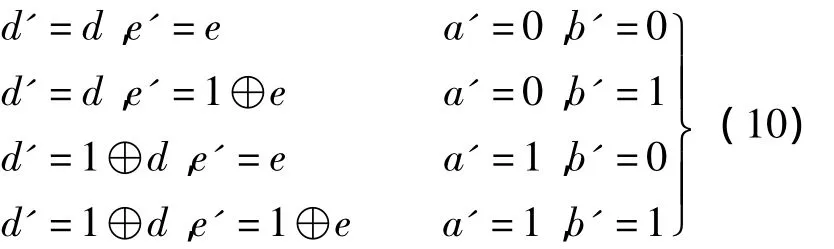
为减少门电路开销，增加了一个辅助位用于产生信号，如图4(b)所示.

根据式(10)形成如图4(c)所示的可逆逻辑电路对d和e进行编码.将图4(b)和图4(c)中的电路进行级联即可形成图4(d)所示的C1函数电路图.图4(d)比图4(a)所示电路仅多了一个辅助位，但减少了4个 CNOT门和1个3控制端的EGT门，开销大大降低.

2.3 可逆比较器的可逆逻辑电路

将C0和C1进行级联即可得到任意nbit可逆比较器.由式(6)可知级联方法为:将非最高位可逆门C0的c1和c2输出作为可逆门C1的d和e输入;将最高位可逆门C0的c1和c2输出和可逆门C1的d'和e'输出作为C1的a和b输入，如图5所示.c1和c2的值为比较结果.

图5所示的comparison门电路图只能进行4 bit的比较.按照级联结构，继续将可逆门C0和C1进行组装，就可以构造出任意n比特的可逆比较器.

2.4 可逆比较器代价分析

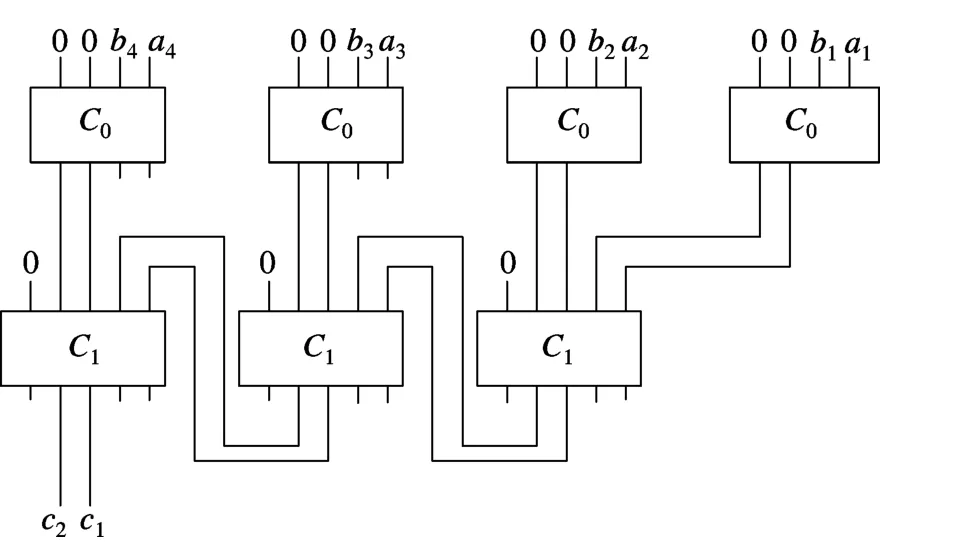
图5 可逆比较器的可逆逻辑电路

可逆门C0需要2个双控制端的EGT门和2个辅助位，产生2个垃圾位.可逆门C1需要4个CNOT门、2个双控制端的EGT门和1个辅助位，产生3个垃圾位.n比特的可逆比较器需要n－1个C1门和n个C0门，因此共需要3n－1个辅助位，4(n－1)个CNOT门，4n－2个双控制端EGT门，产生5n－3个垃圾位.根据Maslov所定义的可逆逻辑电路线性开销［15-16］，可计算出可逆比较器的线性开销为24n－14，因此可逆比较器的代价为Θ(24n).与文献［12］中的方案相比，在比特数为2t时(t为自然数)，本文所提出方案的开销要高.但文献［12］的方案可扩展性差，不同规模的CG电路需要单独设计，且必须扩展为2t比特，而本文提出的方案可扩展为任意比特数的可逆比较器.当比特数不为2t比特时，本文方案的开销低于文献［12］.

2.5 构造 comparator门

在图5所示的门电路后加入CNOT门和Toffoli门(控制位为c1)即可根据最终排序结果将数值较小的值交换到上方.

图6中的comparison门为图5所示电路的简化表示形式，A和B为2个二进制数，粗线表示多位比特线路，细线表示c1.当c1=1时，交换A和B的值;当c1=0时不做任何操作.这样就可将数值较小的数交换到上方的线路中.图6(b)为图6(a)的简化表示形式，称为 comparator门［11］.

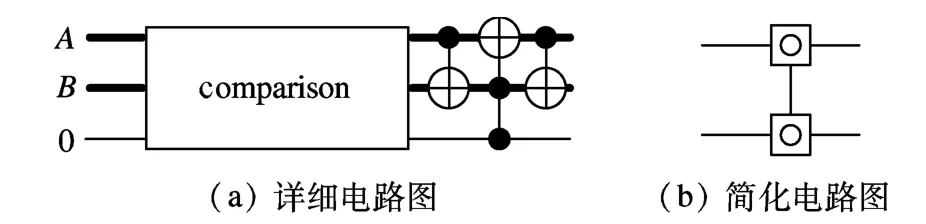
图6 comparator门

3 基于comparator门的败者树排序电路

败者树排序(竞标赛排序)是一种经典的选择排序算法［17］，排序的时间复杂度为O(nlog2n).由于可逆电路具有并行特性，可一次排序得出最大值和最小值，使基于可逆比较器的排序算法的复杂度降低为Θ(n).以下是基于可逆比较器的排序电路的递推生成方法.设n个数的败者树排序函数为TS(n).当只有2个数时，仅需要1个comparator门即可完成排序.

对于超过2 bit的败者树排序电路，可分为如下几个步骤设计.首先，当待排序数的数量n不是2的k次幂时，将其补充为2k个，新添加的数都为无穷大，其中k值根据下式确定:

然后将整个电路层层分解，由较小的模块构造较大的模块，最终构造出n个数的败者树排序电路.败者树排序电路可由下式递归而得:

式中，TM(n)为将2个排好序的数列进行竞标赛排序的模块.

下面以4个数为例，详细说明整个电路的构造方法.图7所示的电路图显示了败者树排序的前2轮比较.其中图7(a)中的电路将上面2个数中较小的交换至最上方，下面2个数中较大的交换至最下方;图7(b)中的电路将上下2个较小的数进行比较，得出最小的值，2个较大的值进行比较得出最大的值.最后只需要对中间2个数进行排序即可排序成功.

图7 败者树前2轮比较

图8(a)给出了4个数败者树排序电路.由层数可知，4个数排序只需要进行3次计算.为了简化电路图，图8(a)电路在下文中用图8(b)表示.

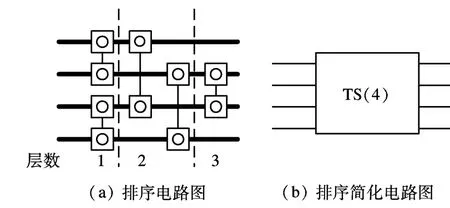
图8 4个数败者树排序可逆逻辑电路

通过分析4个数败者树排序电路，可发现整个电路由2部分构成:① 图7(a)的电路图;② 图8(a)的第2，3两层电路.因此可将整个TS(4)模块分解为2个TS(2)和1个TM(4)模块.

如图9(a)所示，TM(n)电路是排序电路的核心电路.TM(n)模块的主要作用是对2个已经排好序的数列进行败者树排序，每一次排序都要求选择出最小的数和最大的数.下面详细分析TM(n)模块的构造过程.考虑2个数列A=(a0，a1，…，an)和B=(b0，b1，…，bn)，假设A和B都已经排序.先比较a0和b0的值，将最小值交换至a0的位置然后锁定.同时对于任意i∈［1，n］，将ai和bi都进行一次比较，将最大值交换至bn的位置并锁定.然后去掉第一位和最后一位后重复以上过程，直到最终比较an和b0的值为止.

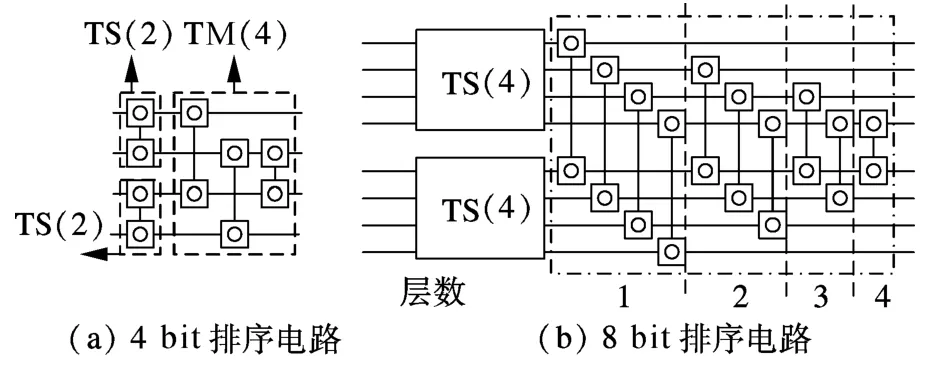
图9 败者树排序可逆逻辑电路递归分解

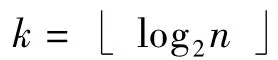
对所有的TM模块层数进行求和，可得到电路的复杂度为

由式(14)可知，可逆败者树排序的时间复杂度为(n).

4 结语

本文基于2种新型可逆门构造可扩展的任意n比特可逆比较器.首先提出了使用递归思想分解任意位电路的方法，并给出了可逆比较器的递归公式.然后使用当前常用的可逆门概念，将电路分解为2个新型可逆门.并且利用编码的概念进行C1可逆门的带无关项可逆逻辑综合，有效地降低了电路的开销.最后将2种新型可逆门级联得到了任意n比特可逆比较器，并给出了可逆比较器电路的代价分析.

利用可逆比较器可以生成comparator门，本文提出了基于comparator门的败者树排序电路，利用电路的并行性质，每经过一层电路可以得到一个最大值和一个最小值，大大加快了排序速度，将时间复杂度降低为(n).

［1］Landauer R.Irreversibility and heatgeneration in the computing process［J］.IBM Journal of Research and Development，1961，5(3):183-191.

［2］Barenco A，Bennett C H，Cleve R，et al.Elementary gates for quantum computation［J］.Physical Review A，1995，52(5):3457-3467.

［3］Song X Y，Yang G W，Perkowski M，et al.Algebraic characterization of reversible gates［J］.Theory of Computing System，2006，39(2):311-319.

［4］Peres A.Reversible logic and quantum computers［J］.Physical Review A，1985，32(6):3266-3276.

［5］Khan M M H A.Design of full-adder with reversible gates［C］//Proceedings of the5th International Conference on Computer and Information Technology.Dhaka，Bangladesh，2002:515-519.

［6］Thapliyal H，Srinivas M B.Novel reversible TSG gate and its application for designing reversible carry look ahead adder and other adder architectures［C］//Proceedings of the10th Asia-Pacific Computer System Architecture Conference.Singapore，2005:775-786.

［7］Haghparast M，Navi K.A novel reversible BCD adder for nanotechnology based systems［J］.American Journal of Applied Sciences，2008，5(3):282-288.

［8］Haghparast M，Jassbi S J，Navi K，et al.Design of a novel reversible multilplier circuit using HNG gate in nanotechnology［J］.World Applied Sciences Journal，2008，3(6):974-978.

［9］Islam M S，Rahman M M，Begum Z，et al.Low cost quantum realization of reversible multiplier circuit［J］.Information Technology Journal，2009，8(2):208-213.

［10］Banerjee A，Pathak A.An analysis of reversible multiplier circuits［EB/OL］.(2009-07-20)［2012-05-14］.http://arxiv.org/abs/0907.3357.

［11］Cheng S T，Wang C Y.Quantum switching and quantum merge sorting［J］.IEEE Transactions on Circuits and Systems，2006，53(2):316-325.

［12］李明翠.基于Toffoli门的可逆数值比较器的设计与优化［J］.华东交通大学学报，2011，28(6):91-95.

Li Mingcui.Design and optimization of reversible numerical comparator based on Toffoli gate［J］.Journal of East China Jiaotong University，2011，28(6):91-95.(in Chinese)

［13］朱皖宁，陈汉武，刘志昊，等.基于Ring-Sum-Expansion范式的Reed-Muller展开式算法［J］.东南大学学报:自然科学版，2010，40(5):932-936.

Zhu Wanning，Chen Hanwu，Liu Zhihao，et al.Reed-Muller expansion algorithm based on Ring-Sum-Expansion［J］.Journal of Southeast University:Natural Science Edition，2010，40(5):932-936.(in Chinese)

［14］王冬，陈汉武，安博，等.量子可逆电路综合的启发式快速匹配算法［J］.东南大学学报:自然科学版，2009，39(5):900-903.

Wang Dong，Chen Hanwu，An Bo，et al.Heuristic fast-matching algorithm for synthesis of quantum reversible logic circuits［J］.Journal of Southeast University:Natural Science Edition，2009，39(5):900-903.(in Chinese)

［15］Maslov D，Young C，Miller D M，et al.Quantum circuit simplification using templates［C］//Proceedings of Design，Automation and Test in Europe.Munich，Germany，2005:1208-1213.

［16］Banerjee A，Pathak A.An algorithm for minimization of quantum cost［EB/OL］.(2010-04-09)［2012-05-14］.http://arxiv.org/abs/0910.2129.

［17］殷人昆，陶永雷，谢若阳.数据结构［M］.北京:清华大学出版社，1997:313-316.

Extensible reversible comparator based on novel reversible gate

Zhu Wanning1Chen Hanwu1，2Ruan Yue1
(1School of Computer Science and Engineering，Southeast University，Nanjing 210096，China)
(2Key Laboratory of Computer Network and Information Integration of Ministry of Education，Southeast University，Nanjing 210096，China)

Abstract:The design proposal for an extensible reversible comparator based on a novel reversible gate is presented to solve the problem that the previous scheme is not extensible.Using the method of recursion，the circuit is decomposed to two kinds of novel reversible gates according to the features of the binary number comparison.And each reversible gate is synthesized with reversible logic.The reversible comparator is realized by cascading these reversible gates.The logical expression of every step is given;the theory of encoding is used to solve logic synthesis with“do not care”set;the detailed scheme for synthesizing reversible comparator is provided.Tournament sort circuit based on reversible comparator is presented，and the asymptotic time complexity of the circuit is decreased to Θ(n).

Key words:reversible comparator;novel reversible gate;recursion

中图分类号:TP387

A

1001－0505(2014)01-0039-06

doi:10.3969/j.issn.1001 －0505.2014.01.008

收稿日期:2013-08-26.

朱皖宁(1983—)，男，博士生;陈汉武(联系人)，男，博士，教授，博士生导师，hanwu_chen@163.com.

基金项目:国家自然科学基金资助项目(61170321)、高等学校博士学科点专项科研基金资助项目(20110092110024).

朱皖宁，陈汉武，阮越.基于新型可逆门的可扩展可逆比较器［J］.东南大学学报:自然科学版，2014，44(1):39-44.［doi:10.3969/j.issn.1001 －0505.2014.01.008］