一种基于OFDM训练序列的精确时延估计方法

黄 毅 胡爱群 成月良 谢胜东，3

(1东南大学信息安全研究中心，南京 210096)(2国电南瑞南京控制系统有限公司，南京 210003)(3南京信息工程大学计算机与软件学院，南京 210044)

一种基于OFDM训练序列的精确时延估计方法

黄 毅1胡爱群1成月良2谢胜东1，3

(1东南大学信息安全研究中心，南京 210096)
(2国电南瑞南京控制系统有限公司，南京 210003)
(3南京信息工程大学计算机与软件学院，南京 210044)

摘 要:提出了一种适用于OFDM系统的基于训练序列的精确时延估计方法.该方法利用频域差分互相关法，精确提取小数时延;在频域补偿小数时延后，再将时域相关法与上升沿法相结合，得到整数时延.由复杂度分析结果可知，当搜索法中获取小数时延的搜索次数大于2时，该方法的小数时延估计计算复杂度与搜索法相比低很多.仿真结果显示，当采样频率为10 MHz、多普勒频移为222.22 Hz、子载波个数为1 024的情况下，根据该方法所实现的时延估计精度能够达到分米级，平均比搜索法高出10 dB;同时，在低信噪比时，该方法比传统的时域相关法具有更健壮的整数时延估计性能.

关键词:差分互相关法;时延估计;OFDM

时延参数被广泛应用于声纳、雷达、生物工程和传感器网络定位中［1-2］.基于到达时间差(TDOA)的定位是一种优秀的定位技术，它需要获得从发射端到3个或更多个接收端的两两时延差.电磁波传播速度是常数，故距离差的估计和时延的估计是等价的.

OFDM系统具有高数据传输能力和对多径的免疫力，是一种很有前景的未来移动通信技术，也是4G移动通信标准的关键规范之一［3］.在OFDM系统中，假设接收机之间的同步已经实现，TDOA信息提取的任务可以转化为获得在每个接收机上的符号定时信息.同步对OFDM系统至关重要，近20年来，学者们已经提出了很多技术来处理符号同步问题［3-11］.同步包括载频同步［5］和符号定时同步［3-8］.本文只关心符号定时同步(时延估计)问题，相关技术可以应用到TDOA信息的提取中.

在过去的十几年中，学者们提出了许多应用于OFDM系统的基于训练序列的时延估计技术.该技术可以被分为2类，即只有整数的时延估计［5-8］和包括整数、小数的时延估计(现实时延估计)［1，3-4］.对于一个 OFDM 接收机而言，整数时延恢复能足够保证数据的解调，但这对于OFDM定位要求是不够的.例如，对于一个30 MHz采样频率的OFDM基带信号，一个采样延迟误差便可导致10 m的测距误差.此外，多径、非视距和多普勒效应也会影响测距误差，从而导致最后的定位精度达不到E911的要求［9］.因此，对于 TDOA信息的提取需要一种更精确的时延估计方法.文献［10］将2个相同符号组成1个前导，用于估计整数时延.文献［11］通过加权一个PN序列到常模零自相关序列(CAZAC)上，得到更加尖锐的相关峰.文献［12］先对训练序列进行循环相关预处理，以改善估计性能.文献［13］扩展了文献［12］的方法，得到了更有效的相关测度以适应恶劣的信道，但是这种处理实际上是高阶相关的，增加了计算复杂度.文献［12-13］的方法都是独立于序列结构的.然而，上述这些方法都只能进行整数时延估计.

对于现实应用中的时延估计问题，文献［1］提出了相关法，即先小数补偿接收到的OFDM基带信号，然后通过检测相关峰得到整数时延，所得结果能够达到E911的定位要求.文献［2］提出了差分相关法，即使用差分互相关测度来得到时延的厘米级精度，但是，该模型是基于加性高斯白噪声(AWGN)信道的，在多径条件下，估计性能会严重恶化，特别是在信道的首径不是主径的情况下.OFDM时延估计的另一大类是基于非训练序列的［5］，然而，这些方法大部分都不能处理小数时延.

本文提出了一种面向OFDM系统的基于训练序列的精确时延估计方法.该方法利用差分互相关法精确提取小数时延，然后将相关法和上升沿法相结合，得到整数时延估计.该方法不需要信道的任何先验信息.实验结果显示，即使在低信噪比下，该方法仍具有高的时延估计精度.

1 系统模型

考虑一个包含N个子载波的OFDM系统，用d(k)表示第k个子载波上的复数据，则连续时间基带信号可以表示为

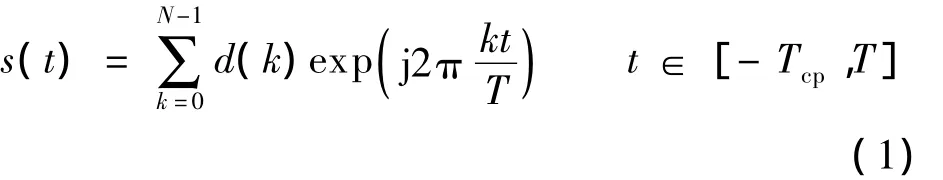
式中，t为连续时间;Tcp为保护间隔;T为有效的OFDM符号周期.用采样周期Ts对s(t)进行离散化，或者在发送之前先对d(k)进行IFFT处理，得到的离散信号为

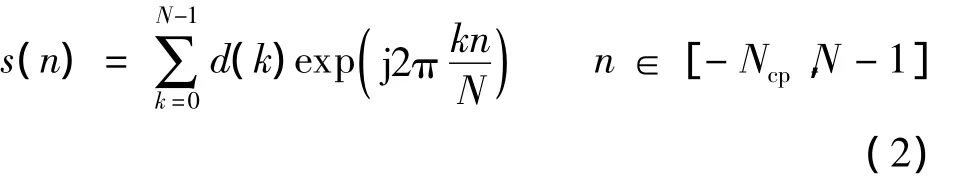
式中，n为离散时间;Ncp为归一化CP的长度;T=NTs;Tcp=NcpTs.

假设信号通过一个多径信道，则接收到的基带信号为

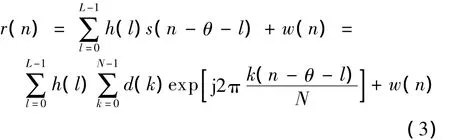
式中，h(l)为第l条径的系数;θ为归一化时延;w(n)为复高斯白噪声.

2 两步相关法

2.1 传统相关法

对于一般的训练序列，常采用相关法获得相关峰，以此作为整数时延估计值，即

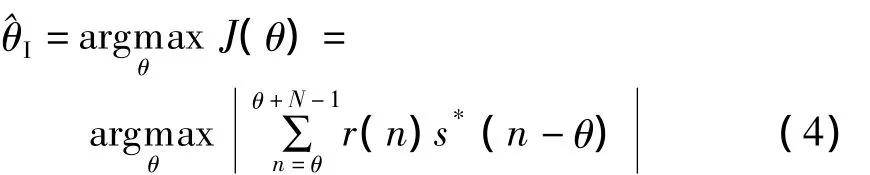
式中，J(θ)为代价函数.

然而，当有小数时延存在时，相关峰会被弱化，且产生旁瓣，使得估计性能大大降低［1］.文献［1］提出利用频域相位补偿小数时延，但这种方法属于搜索方法，每次搜索需要进行FFT处理和IFFT处理，计算复杂度较大.本文采用差分法提取小数时延，从而减小了复杂度，提高了估计精度.

2.2 两步相关法

假设信道中有一条径是主径(即系数最大)，先用文献［2］中的频域差分相关法得到精确的小数时延，然后将传统的时域相关法与上升沿法相结合，得到整数时延.

首先，对r(n)进行FFT处理，得到频域接收信号，即

然后，对式(6)进行迟滞m的差分相关处理，即

在l'为主径的情况下，I4(m)+W‴(m)都可以视为噪声.

最后，时延θ+l'可以由下式估计得到:

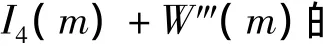
对接收到的频域信号进行频域补偿，可避免小数时延.为方便表示，忽略噪声项，即

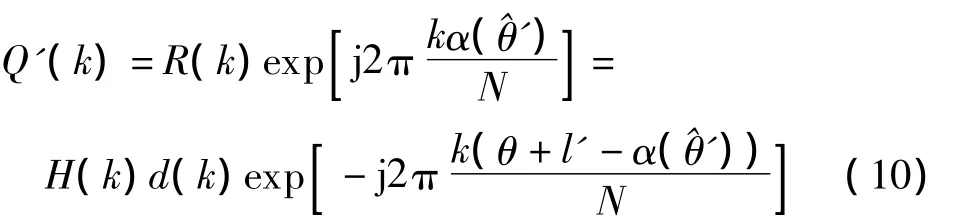
式中，α(')为'的小数部分;H(k)为信道频域响应.将Q'(k)变到时域，如果小数时延估计准确，则得到的时域信号仅剩下整数时延.通过解式(4)，并结合上升沿法，便可得到第1条径的时延I(即整数时延估计).至此，得到的时延估计为

2.3 计算复杂度分析

下面采用复乘的次数来评价计算复杂度.此处的整数时延估计与文献［1］中的相关法相同，仅小数时延估计不同.对于文献［1］方法中的小数时延估计，需要进行线性搜索，每次需要1次FFT处理、1次N点的复乘计算、1次IFFT处理和U次相关处理，即共需要2Nlog2N+(U+1)N次复乘计算.而对于差分相关法计算小数时延，需要1次2N点的FFT处理、1次2N点的复乘计算、1次2N点的IFFT处理、1次N点的FFT处理、1次N点的复乘计算、N/2－1次的复乘计算和N/2－1次的求幅角计算，由于CORDIC算法可以用于求幅角计算且复杂度大大降低，故此处忽略幅角计算，总共需要4Nlog2N+13N/2－1次复乘计算.差分相关法不是搜索法，当搜索法中获取小数时延的搜索次数大于2时，差分相关法的小数时延估计计算复杂度与搜索法相比低很多，因此，一般情况下所提方法的计算复杂度大大低于文献［1］中的相关法.

3 仿真结果

采用Jakes多径信道模型来模拟信道，信道模型参数见表 1.训练序列采用 Zad-Off序列［14］，OFDM系统参数如下:N=1 024，Ncp=64，载频fc=2 GHz，采样周期Ts=0.1 μs，移动速度为 120 km/h，相应的多普勒频移为222.22 Hz.

表1 Jakes多径信道模型参数

将文献［1］中的相关法和文献［2］中的差分相关法与本文提出的两步相关法进行比较.其中，相关法中小数时延估计采用的是一维搜索法——0.618法，终止精度级设定为0.001.将这3种方法的时延估计精度取为500次独立运行的平均值.

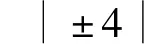
图1 最后时延估计中整数部分的误差直方图

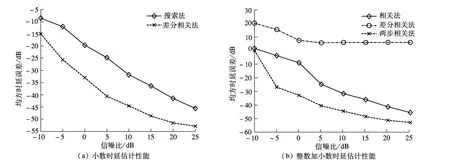
图2 时延估计的均方误差性能

图2(a)为最后时延估计中小数部分的均方误差性能.由于两步相关法中小数时延估计采用的是差分相关法，因此这幅图中只显示了相关法中搜索法和差分相关法的估计性能，且后者比前者约有10 dB的性能改善.图2(b)为整数加小数时延估计性能.由图可知，整数部分的误差导致3种方法最后估计性能的退化.但是，两步相关法在SNR≥0 dB时，精度和图2(a)中一样，这是由于其整数估计的健壮性(见图1);而另外2种方法的时延估计性能存在不同程度的下降，且差分相关法恶化更严重.此外，两步相关法所实现的时延估计精度在SNR≥0 dB的情况下能够达到分米级.

4 结语

OFDM系统中TDOA信息的提取一直是研究热点.为了得到现实中的时延估计，本文提出了一种基于训练序列的精确时延估计方法.该方法整合了差分互相关法提取小数时延的精确性和相关法求整数时延的健壮性，而且不需要信道和噪声的先验信息.一般情况下，该方法的小数时延估计计算复杂度比搜索法低很多.实验结果显示，即使在低信噪比下，该方法仍具有较高的现实时延估计精度.

［1］Ni H，Ren G，Chang Y.A TDOA location scheme in OFDM based WMANs［J］.IEEE Transactions on Consumer Electronics，2008，54(3):1017-1021.

［2］Dai L，Wang Z，Wang J，et al.Positioning with OFDM signals for the next-generation GNSS ［J］.IEEE Transactions on Consumer Electronics，2010，56(2):374-379.

［3］Yang B，Letaief K B，Cheng R S，et al.Timing recovery for OFDM transmission［J］.IEEE Journal on Selected Areas in Communications，2000，18(11):285-289.

［4］Zhou H，Huang Y F.A maximum likelihood fine timing estimation for wireless OFDM systems［J］.IEEE Transactions on Broadcasting，2009，55(1):31-41.

［5］Rotoloni M，Tomasin S，Vangelista L.Maximum likelihood estimation of time and carrier frequency offset for DVB-T2 ［J］.IEEE Transactions on Broadcasting，2012，58(1):77-86.

［6］Abdzadeh-Ziabari H，Shayesteh M G，Manaffar M.An improved timing estimation method for OFDM systems［J］.IEEE Transactions on Consumer Electronics，2010，56(4):2098-2105.

［7］Baek J S，Seo J S.Effective symbol timing recovery based on pilot-aided channel estimation for MISO transmission mode of DVB-T2 system ［J］.IEEE Transactions on Broadcasting，2010，56(2):193-200.

［8］Wang C L，Wang H C.Optimized joint fine timing synchronization and channel estimation for MIMO systems ［J］.IEEE Transactions on Communications，2011，59(4):1089-1098.

［9］Federal Communications Commission.Revision of the commissions rules to ensure compatibility with enhanced 911 emergency calling systems［R］.Washington DC:FCC，1996.

［10］Schmidl T M，Cox D C.Robust frequency and timing synchronization for OFDM ［J］.IEEE Transactions on Communications，1997，45(12):1613-1621.

［11］Ren G，Chang Y，Zhang H，et al.Synchronization method based on a new constant envelop preamble for OFDM systems［J］.IEEE Transactions on Broadcasting，2005，51(1):139-143.

［12］Kang Y，Kim S，Ahn D，et al.Timing estimation for OFDM systems by using a correlation sequence of preamble［J］.IEEE Transactions on Consumer Electronics，2008，54(4):1600-1608.

［13］Abdzadeh-Ziabari H，Shayesteh M G.Robust timing and frequency synchronization for OFDM systems［J］.IEEE Transactions on Vehicular Technology，2011，60(8):3646-3656.

［14］Chu D C.Polyphase codes with good periodic correlation properties［J］.IEEE Transactions on Information Theory，1972，18(4):531-532.

http://journal.seu.edu.cn

Accurate time delay estimation scheme based on training sequence in OFDM systems

Huang Yi1Hu Aiqun1Cheng Yueliang2Xie Shengdong1，3
(1Research Center of Information Security，Southeast University，Nanjing 210096，China)
(2NARI-TECH Control Systems Co.，Ltd.，Nanjing 210003，China)
(3Computer and Software Institute，Nanjing University of Information Science and Technology，Nanjing 210044，China)

Abstract:An accurate time delay estimation scheme based on training sequence in orthogonal frequency division multiplexing(OFDM)systems is proposed.The scheme employs differential crosscorrelation technology to extract the fractional delay in the frequency domain.Then，correlation technology and leading edge method are used to obtain the integer delay after compensation for the fractional delay in the frequency domain.The complexity analysis results show that if the number of searches for estimating the fractional delay is greater than two in the searching method，the computational complexity in the fractional delay estimation of the proposed algorithm is much lower than that of the searching method.The simulation results show that the proposed scheme can achieve an accuracy of decimeter level in the sampling frequency of 10 MHz，the Doppler shift of 222.22 Hz and the number of subcarriers of 1 024，which is about 10 dB higher than that of the searching method on average.Moreover，the proposed scheme has a more robust integer delay estimation performance than the traditional correlation technology even at low signal-to-noise ratio(SNR).

Key words:differential cross-correlation;time delay estimation;orthogonal frequency division multiplexing(OFDM)

中图分类号:TN929

A

1001－0505(2014)01-0007-05

doi:10.3969/j.issn.1001 －0505.2014.01.002

收稿日期:2013-05-31.

黄毅(1984—)，男，博士生;胡爱群(联系人)，男，博士，教授，博士生导师，aqhu@seu.edu.cn.

基金项目:国家高技术研究发展计划(863计划)资助项目(2013AA014001)、“十二五”国家科技支撑计划资助项目(2012BAH38B05).

黄毅，胡爱群，成月良，等.一种基于OFDM训练序列的精确时延估计方法［J］.东南大学学报:自然科学版，2014，44(1):7-11.［doi:10.3969/j.issn.1001 －0505.2014.01.002］