轻型货车用扭转缓冲器的优化设计

王灵犀,曹雪飞

(沈阳理工大学 汽车与交通学院,辽宁 沈阳 110159)

轻型货车用扭转缓冲器的优化设计

王灵犀,曹雪飞

(沈阳理工大学 汽车与交通学院,辽宁 沈阳 110159)

设计的扭转缓冲器以体积最小、质量最轻为优化目标，建立扭转缓冲器多目标优化设计的数学模型。采用统一目标法对帘布层进行优化，并借助Matlab编制多目标优化设计程序，进行优化运算。结果表明：采用该种方法可获得不同要求的设计方案，提高设计效率。

扭转缓冲器；帘布层；多目标优化

由于货车的行驶环境比较恶劣，传动系中的冲击载荷较大，对高速柴油机的可靠性和使用寿命均构成威胁。通过在传动系中加装扭转缓冲器可减少传递给发动机的动载荷，从而减少对发动机的损坏。

目前对扭转缓冲器研究大部分基于单目标优化理论，重点集中在结构改进上。刘卫真[1]利用单目标优化理论对钛合金扭转缓冲器研究。于海江[2]利用多目标优化理论对弹簧型扭转缓冲器的结构进行研究。刘文清[3]对扭转缓冲器结构研究采用单目标优化设计方法。大部分扭转缓冲器的研究都利用了单目标优化设计理论，而利用多目标优化在结构上使用弹簧扭转缓冲器研究。本文采用多目标优化方法设计钢丝帘布层为主要结构的扭转缓冲器，降低传动系扭转刚度，减轻发动机的负载。

1 建立扭转缓冲器多目标优化设计数学模型

本文所设计的扭转缓冲器是利用橡胶帘布层为主要零件结构进行缓冲作用的装置。该缓冲器的主体部分由传力销、钢丝帘线、橡胶包裹层构成。缓冲原理为：由于钢丝帘线是弯曲的(有弧度)，在传力伸直过程中会挤压内圈的橡胶体，橡胶体的变形将允许椭圆形的钢丝帘线圈伸缩，使传动轴产生较大的弹性变形角，降低传动轴的扭转刚度，起到缓冲作用。缓冲器中的橡胶块起支撑弹簧作用；橡胶还包裹固定钢丝帘线，其与钢丝帘线之间的摩擦可提供阻尼，但由于该摩擦会导致橡胶块受损而应在设计中尽量避免；缓冲器的阻尼主要来自橡胶块内部的迟滞能量损失。本设计的优化主要考虑钢丝帘线的强度，对橡胶阻尼暂不考虑。

采取多目标优化方法对帘布层钢丝进行优化。借助Matlab优化工具进行求解，可得到优化设计参数[4]。所设计的扭转缓冲器如图1所示。

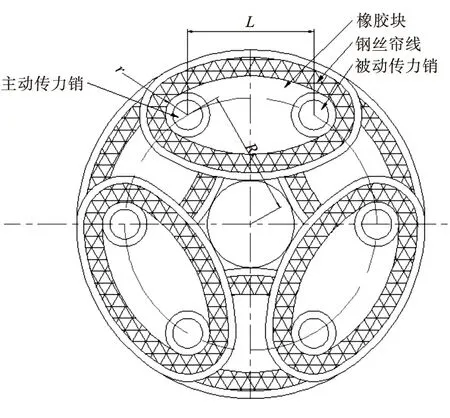
图1 扭转缓冲器

1.1 设计变量的确定[5]

图2为设计的扭转缓冲器的结构力学图。

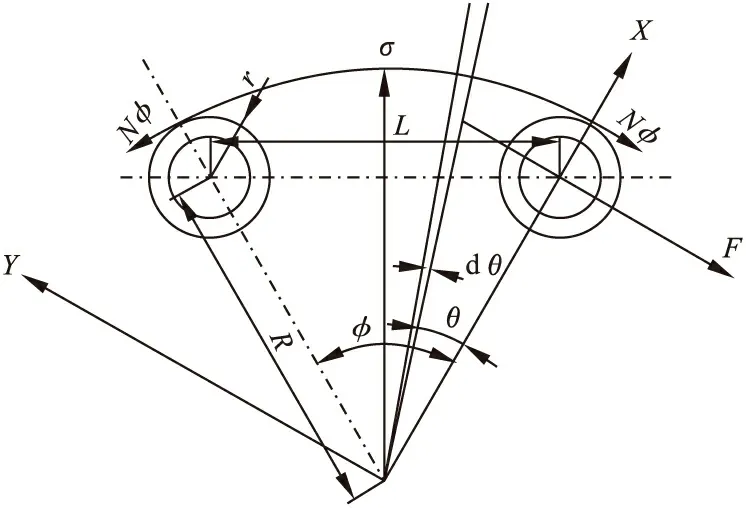
图2 结构力学图

本文选取R、r、L为设计变量，构成设计向量：

X=[R，r,L]T=[x1,x2,x3]T

式中：R为扭转缓冲器的中心到销孔中心的距离；r为扭转缓冲器圆柱销外边缘半径；L为扭转缓冲器两个销孔中心距；xi(i=1,2,3)为设计变量的函数。

1.2 目标函数的确定[6]

本文的优化目标是：在保证原缓冲器机械强度的前提下缩小其体积、减轻其重量。故据此设计目标函数。

(1)体积目标函数

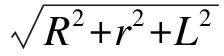
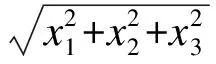
式中R、r、L均为决定缓冲器体积的主要设计参数，将其几何平均值M最小作为优化目标。

(2)质量目标函数

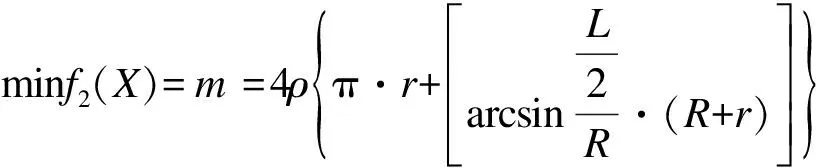
式中R、r、L均为决定缓冲器质量的主要设计参数。将其帘布层中钢丝的质量m最小作为优化目标。ρ为钢丝材料密度(7.85×10-3g/mm3)

1.3 约束条件的确定

在优化目标函数的同时，设计变量的取值必须服从各种规律和限制，即构成设计的约束条件。按照设计变量的性质不同，约束有性能约束和边界约束两类。

1.3.1 性能约束

性能约束是根据设计性能或指标要求而定的一种约束条件，如零件的强度条件、刚度条件、稳定性条件、模态条件、重量条件均属于性能约束。通常表达成如下形式

gj(x)≤0(j=1,2,…,n)

由于帘布钢丝工作时处于抗拉状态(本次优化只考虑最大扭矩时钢丝强度约束)，所以帘布层钢丝强度要满足一定约束条件[7]：

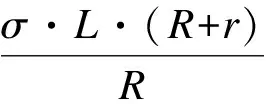
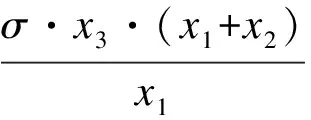
式中，σ为橡胶对钢丝的内侧应力，取常数，Tmax为钢丝所承受的最大抗拉强度。

1.3.2 边界约束

边界约束又称区域约束或辅助约束，用于限制某个设计变量(结构参数)的变化范围或某组变量之间的相对关系，以防止在优化设计过程中出现不切实际的量值。通常表达成如下形式：

Xmin≤X≤Xmax

(1)扭转缓冲器的中心到销孔中心的距离

Rmin≤R≤Rmax

g1(x)=Rmin-x1≤0

g2(x)=x1-Rmax≤0

(2)扭转缓冲器圆柱销外边缘半径

rmin≤r≤rmax

g3(x)=rmin-x2≤0

g4(x)=x2-rmax≤0

(3)扭转缓冲器两个销孔中心距

Lmin≤L≤Lmax

g5(x)=Lmin-x3≤0

g6(x)=x3-Lmax≤0

综上所述，可建立扭转缓冲器的多目标优化数学模型。

即X=[R,r,L]T=[x1,x2,x3]T

s.tgj(x)≤0(j=1,2,…,11)

2 多目标优化设计及工程实例

2.1 多目标优化及目标函数确定方法

利用多目标优化求解的方法很多，本文将多目标优化问题求解时做适当的变化，采用统一目标法又称综合目标法，将多目标优化问题通过一定方法转化为统一目标函数，目标优化问题的评价函数既该函数，然后利用单目标函数优化方法求解。这里是采用线性加权法把多目标优化问题转化为评价函数[8]。

minF(X)=min[w1f1(X)+w2f2(X)]

wj(j=1,2)为加权因子且

w1+w2=1,wj≥0

采用容限法选取加权因子。即：若已知某分目标函数fj(X)的变动范围为

αj≤fj(X)≤βj

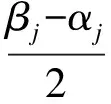
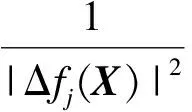
2.2 工程实例

设计扭转缓冲器中帘布层中最大工作扭矩Tmax=432N·m结构设计要求:

60mm≤R≤75mm，20mm≤r≤35mm，60mm≤L≤80mm。按照质量最轻，体积最小进行优化。

3 对扭转缓冲器进行优化求解

3.1 数学模型

(1)根据给定的工作环境和结构设计要求,依据2.1介绍的方法,其目标函数为minF(X)=min[w1f1(X)+w2f2(X)]

(2)根据1.3约束条件,可得相应的约束函数:

g(1)=60-x1

g(2)=x1-75

g(3)=20-x2

g(4)=x2-35

g(5)=60-x3

g(6)=x3-80

g(7)=7800×10·x3·(x1+x2)-432

3.2 利用Matlab优化求解

(1)多目标优化问题在Matlab中主要由函数fgoalattain来实现，根据数学模型编写目标函数、约束条件和fgoalattain运行程序。

(2)根据传统机械设计原理及经验设计出扭转缓冲器,选定扭转缓冲器的中心到销孔中心的距离R，扭转缓冲器圆柱销外边缘半径r和扭转缓冲器两个销孔中心距L的设计尺寸为初始点，即X0=[70,25,70]，根据编辑好的优化设计程序可解得设计变量和目标函数值:

xopt=68.0184 24.0135 67.0208

fopt=100.5289 3.9301

取整后

R=68mmr=24mmL=67mm

表1 优化结果对比

由表1可知，在满足钢丝的强度约束条件下，R减小了2mm,r减小了1mm,L减小了3mm,帘布层的几何平均数减小，缓冲器的体积缩小,重量减小,满足了工程实际应用。

4 结束语

建立了扭转缓冲器的多目标优化数学模型，利用Matlab优化工具箱进行优化分析，并计算出优化结果。结果表明，采用该种方法，可获得不同要求的设计方案，提高设计效率。由优化结果对比可知，新方案比原设计方案，重量下降了24%，帘布层体积几何平均数减小18%，扭转缓冲器的体积得到减小，同时满足约束条件,结构更加紧凑，节省安装空间，优化综合效果显著。实践中对算出的结果还需根据实际情况进行调整。

[1]刘卫真.钛合金柔性联轴节设计优化与疲劳验证[D].上海:上海交通大学，2009.

[2]于海江.扭转缓冲器弹簧的多目标优化设计[J].沈阳理工大学学报,2012,28(3):68-72.

[3]刘文清.扭转缓冲器可靠性单目标优化设计[J].山西机械,2007,13(4):62-78.

[4]龚纯,王正林.精通Matlab最优化计算[M].北京:电子工业出版社，2012.

[5]郭建瑞,张彪.联轴器系列设计方法探讨[J].机械设计,1995,13(4):62-78.

[6]揭琳锋.基于复合材料理论的轮胎帘线受力模型及测试技术研究[D].镇江:江苏大学，2010.

[7]李轩.大型肋骨冷弯机结构优化研究[D].武汉:武汉理工大学,2008.

[8]耿玉磊,张翔.多目标优化的求解方法与发展[J].机械研究与应用,2009,11(4):42-51.

OptimizationDesignofReverseBufferinLightTrucks

WANG Lingxi，CAO Xuefei

(Shenyang Ligong University,Shenyang 110159 China)

Focus on designing a reverse buffer of minimum size and weight.The mathematical model of multi-objective optimization design of reverse buffer is established.Unified method is employed to optimize the cord fabric layer.Matlab is used for multi-objective optimal design program and optimization calculation.The results show that,using this method,different requirements of the design schem can be satisfied,the design efficiency can be also greatly improved.

reverse buffer；cord fabric layer；multi-objective optimization

2013-09-10

王灵犀(1956—)，男，教授，研究方向：车辆工程.

1003-1251(2014)04-0067-04

TH122

A

赵丽琴)