标准映射和Lorenz混沌系统彩色图像加密算法

祁 燕，刘丽萍

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)

标准映射和Lorenz混沌系统彩色图像加密算法

祁 燕，刘丽萍

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)

基于标准映射和Lorenz混沌映射，针对RGB彩色图像，提出一种混沌加密算法。利用标准映射产生的非线性混沌序列，对图像像素位置进行置乱；利用Lorenz混沌系统的三维优势，结合彩色图像的R、G、B分量，对像素进行扩散。通过置乱和扩散两个步骤的混沌映射完成图像的加密，克服了单一加密安全性不高的缺点。相关实验和分析表明，该算法有良好的安全性和加密性能。

混沌系统；图像加密；标准映射；Lorenz系统

数字图像在人们日常生活中的使用越来越广泛，但随着计算机网络和多媒体等技术的迅猛发展，数字图像的版权和安全问题受到社会广泛的关注。围绕安全问题，广大学者开展了各种研究工作，图像加密是其中一个重要研究分支。图像加密属于密码编码技术，是集数学、密码学、信息论、计算机等多门学科的交叉学科，通过对数字图像进行像素位置和灰度的变换，隐藏图像原有信息，实现数字图像基于内容的保护，该技术在保密通信、信息隐藏和数字水印等领域中有广泛的应用。

目前，国内外专家学者对图像加密的研究主要集中在空间域、变换域、基于混沌、基于神经网络、基于细胞自动机、量子密码技术等[1-3]。其中，混沌是一种具有特殊性质的复杂动力学行为，它具有对初始条件和系统参数的极度敏感性、运动轨迹的无规则性、内随机性、有界性和遍历性等特性。用混沌系统来产生数字混沌序列是目前常用的图像加密方法。混沌图像加密大多是针对图像的特点，在空域和频域上对其进行加密，目前研究比较多的是利用混沌映射对图像进行空域变换，最具代表性的映射方法有[4-6]：面包师(Baker)映射、猫(Cat)映射、标准(Standard)映射等。

本文提出一种针对彩色图像的双重加密算法。首先，对原始图像像素的位置采用标准映射混沌序列进行置乱；然后，分别对图像RGB分量的像素值采用Lorenz混沌序列进行扩散变换；最后，将各分量合成为密文图像。

1 图像加密算法

1.1 标准映射

本文加密算法先对图像像素位置进行置乱，常用的置乱变换有Arnold 变换、幻方变换、Cat映射等。置乱方式可分为直接法和分块法，直接法对图像各个像素点的坐标位置直接进行变换；分块法先对图像进行分块，然后在块内进行局部置乱。但是，这些置乱变换多为线性变换，与密钥无关，其安全程度不高，且分块后的置乱有局部性，置乱程度不高。因此，本文采用具有非线性特征的标准映射对图像进行非线性置乱。

标准映射具有极其丰富的动力学性质，是混沌系统的基本模型之一，反映了弹跳球模型在高弹跳情形下的二维映射。标准映射定义如下[7]：

S(x,y)=(S1,S2)=((x+y)mod2π,

(y-ksin(x+y))mod2π)

(1)

式中参数k为正常数。式(1)可推广为

(2)

式(2)的逆为

(3)

为设计置乱变换系统，需要将式(2)和式(3)离散化，由此可设计置乱变换为

(4)

本文对分辨率为256×256、灰度级为256的Lena图像采用标准映射进行像素置乱实验的结果如图1所示。

图1 标准映射像素置乱结果

由图1可以看出，图像置乱可以有效地打乱原图的次序，但像素值并未改变，离散后的混沌映射变为周期性，且置乱后的直方图与原直方图相同。在现代密码体制下，任何图像置乱算法都可通过穷举法来破密，因此为了增强加密效果，需要进行扩散过程以改变图像像素值，弥补置乱加密有周期性的不足，也能使加密图像的直方图统计呈均匀分布。

1.2 Lorenz混沌映射

Lorenz混沌映射是一个三维混沌系统，这一特征能与彩色图像的RGB三个分量结合起来。Lorenz混沌系统的动力学方程如下[8]：

(5)

式(5)中，σ、γ和b是系统参数。Lorenz系统在保持σ和b取值不变，γ>24.74时，Lorenz系统进入混沌状态。一般来说，系统参数取典型值σ=10、γ=28和b=8/3。

本文用Lorenz系统产生的三维混沌序列对彩色图像的RGB分量分别进行扩散变换，与二维混沌系统相比结构更复杂，系统变量序列更不可预测，因此能达到更好的加密效果。

1.3 算法流程

本文图像加密算法采用像素位置置乱和像素值扩散相结合的加密方案，如图2所示。先用标准映射对原始图像像素位置进行非线性置乱；然后利用Lorenz三维映射的三个参数，构造混沌序列，分别对应彩色图像的R、G、B分量，实现像素的扩散过程。

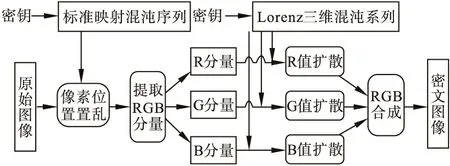
图2 本文加密算法流程

算法具体步骤如下：

(1)读入原始图像和密钥K1=(x(1),y(1),z(1),h)、K2=(μ2,c(0),k2)、K3=(μ3,c′(0),k3)；

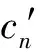
(4)依次对原始图像中的每个像素点，应用式(4)迭代进行置乱变换；

(5)将K1代入式(5)，生成混沌序列x(i)、y(i)和z(i)；

(6)通过mod(256x(i),256)将序列转换到[0,255]之间；

(7)从彩色图像中分别提取R、G、B分量，分别对应混沌序列x(i)、y(i)和z(i)，对各分量像素值按行优先序列进行异或运算；

(8)将R、G、B分量运算结果合成彩色图像，保存并输出密图。

解密算法是加密的逆过程。

2 仿真实验及性能分析

2.1实验结果

为验证本文提出的加密算法，对lena和logo彩色图像进行了相关实验和性能分析。实验环境为2.5GHz CPU、2G内存、Windows XP操作系统、Matlab软件工具。实验对象为24位真彩色图像，分辨率为256×256。参照经典值，密钥设为

K={K1,K2,K3}

其中

K1=(1.1840,1.3627,1.2519,0.01)

K2=(3.9,0.3,10000)、K3=(3.6,0.5,10000)。

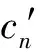
对lena图像进行标准映射置乱变换，迭代次数分别为1、2和30时的置乱结果如图4所示。折中考虑置乱效果和时间复杂性，后续实验中迭代次数取30次。

在lena图像中随意取三个像素点，经过30次迭代后，其位置的变化如图5所示。可以看出置乱位置在整个图像区域内分布较为均匀。

对lena和logo图像的加密和解密结果如图6所示。

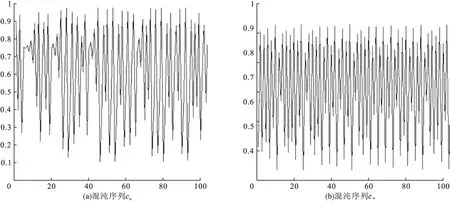
图3 部分混沌序列

图4 不同迭代次数的置乱

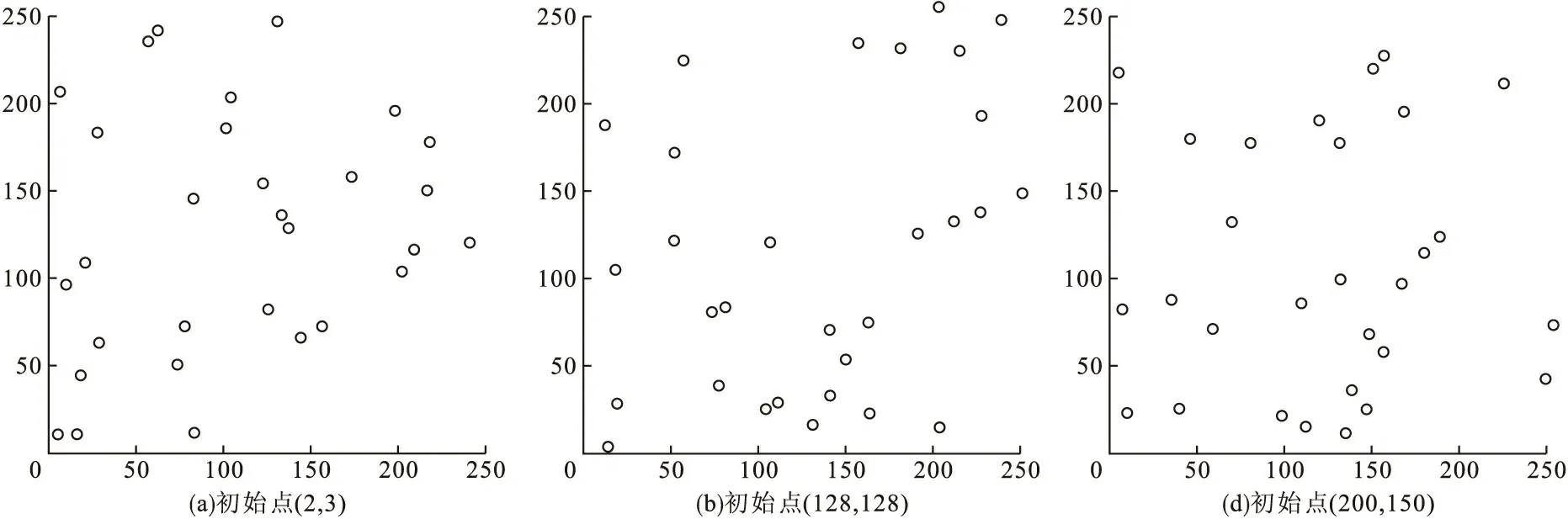
图5 像素点30次置乱

2.2 相关性分析

原始图像中，相邻像素之间的相关性很强，如图4a～图4c，图像加密则应该尽可能降低其间的相关性。相邻像素相关系数ρxy即为评价加密效果的重要客观评价指标。相关系数ρxy可按如下公式计算：

(6)

式中：

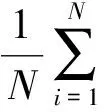
本文分别在logo原图与密图的R、G、B三个分量中随机选取1500对像素点，分别从水平、垂直和对角三个方向进行相关性分析实验，其中R分量的相关性结果如图7所示，G和B分量的相关性分析结果与R分量的结果一致。

图6 本文算法加解密结果

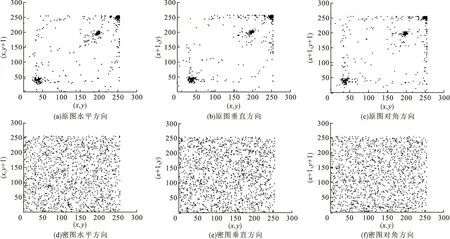
图7 logo原图与密图R分量的相邻像素相关性

由图7a～图7c可知，原图三个方向像素点之间的相关性在y=x的直线附近分布较为集中，说明其相邻像素间的相关性较强。而图7d～图7f中，三个方向的相关性均匀分布，说明密图中相邻像素相关性较弱。相关系数ρxy具体的定量分析如表1所示，并且与S_L算法的数据进行了对比。

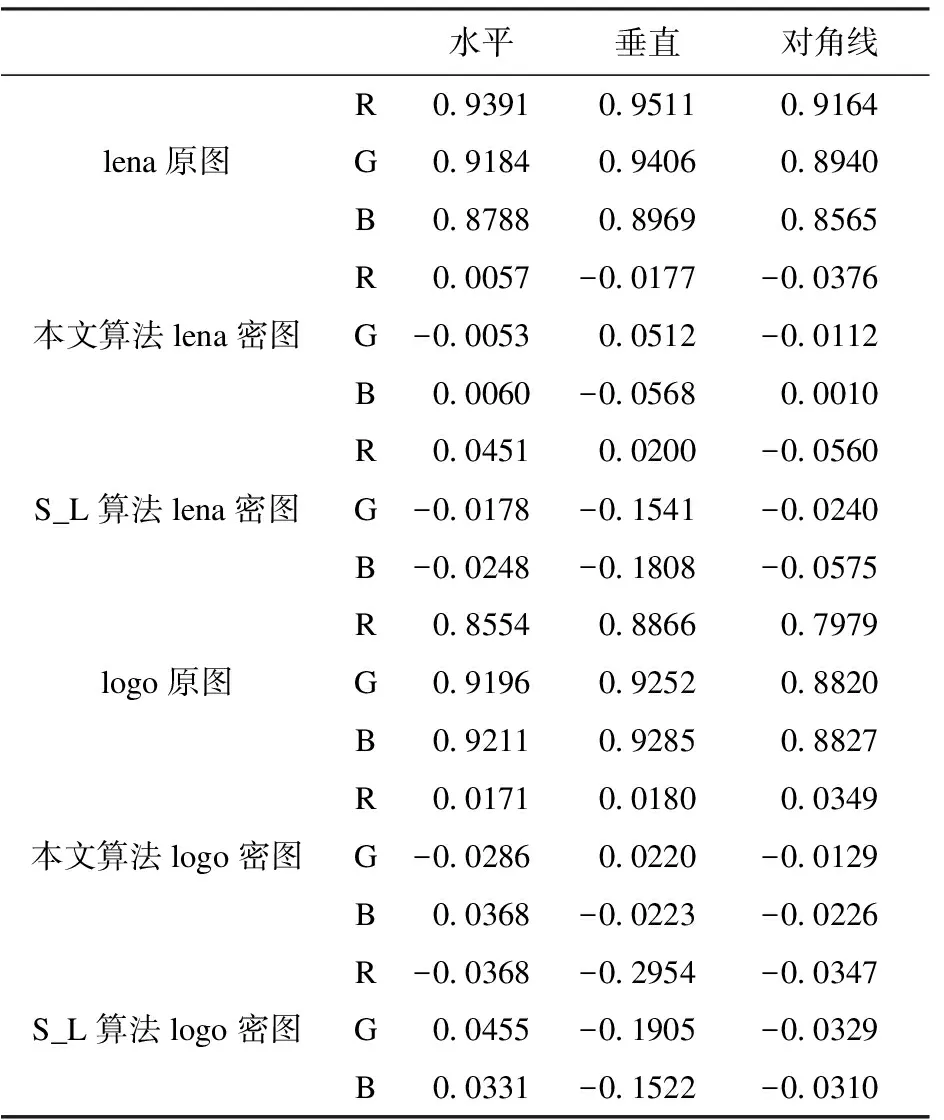
表1 原图与密图相关系数ρxy

S_L算法采用标准映射进行置乱，Logistic混沌进行扩散。为了降低对比实验结果的随机性，实验中选用相同的密钥参数，而且选取像素点对时设置了随机序列种子，以保证随机点对的一致性。原图像与密图的相关系数实验数据说明本文提出的加密算法极大地降低了图像的相关性，具有较好的扩散能力，加密效果好。不同算法的对比实验数据说明本文算法与S_L算法相比有较为明显的优势。

2.3 直方图分析

对logo原图和密图进行直方图分析的结果如图8所示。

由图8可知，加密后图像的直方图与原图像的直方图相比，其分布比较均匀，从而加密效果更加理想，能有效地抵抗统计分析。

2.4 密钥敏感性分析

为验证密钥的敏感性，本文对Lorenz混沌系统的正确密钥作细微的调整，然后进行解密。正确密钥为K1=(1.1840,1.3627,1.2519,0.01)，错误密钥分别取值为

Ke1=(1.1840+10-15,1.3627,1.2519,0.01)、

Ke2=(1.1840,1.3627+10-15,1.2519,0.01)、

Ke3=(1.1840,1.3627,1.2519+10-14,0.01)、

Ke4=(1.1840,1.3627,1.2519,0.01+10-16)，logo密图解密结果如图9所示。

图8 logo原图与密图直方图

图9 错误秘钥解密结果

由图9可知，当错误密钥与正确密钥之差仅为10-14(接近精度极限)时，仍不能正确解密。因此本文加密算法对密钥具有极强的敏感性。

本文加密算法中Lorenz映射密钥K1=(x(1),y(1),z(1),h)可取任意实数，精度为10-16，因此该算法的密钥空间极大，从而使得对密图的暴力破解几乎不可能。

3 结论

针对RGB彩色数字图像，提出了一种将标准映射和Lorenz三维混沌系统相结合的加密算法，并对该算法进行了实验和性能分析。标准映射具有非线性特征，且不具有周期性，因此安全性更高。Lorenz三维混沌序列运算掩盖了混沌子序列的分布特性，改变了子混沌系统的动力学行为。实验证明，该算法具有良好的加密效果、极高的密钥敏感性及较大的密钥空间，能有效抵制暴力破解和统计攻击。

[1]刘家胜.基于混沌的图像加密技术研究[D].合肥:安徽大学,2007.

[2] 张晓强,王蒙蒙,朱贵良.图像加密算法研究新进展[J].计算机工程与科学,2012,34(5):1-6.

[3] 文昌辞,王沁,苗晓宁,等.数字图像加密综述[J].计算机科学,2012,39(12):6-9,24.

[4] Fridrich J. Symmetric ciphers based on two-dimensional chaotic maps[J].Int J Bifurcation and Chaos,1998,8(6):1259-1284.

[5] 胡春强,邓绍江,秦明甫,等.基于Logistic与标准映射的数字图像加密算法[J].计算机科学,2010,37(12):57-59.

[6] 盛苏英,吴新华.一种新的图像加密算法研究与应用[J].微电子学与计算机,2011,28(2):124-128.

[7] N.K.Pareek,V.Patidar,K.K.Sud.Image encryption using chaotic logistic map[J]. Image and Vision Computing,2006,(24):926-934.

[8]Chaohai Tao,Chunde Yang. Three control strategies for the Lorenz chaotic system[J].Chaos,Solitons & Fractals,2008,35(5):1009-1014.

ColorImageEncryptionAlgorithmBasedonStandardandLorenzChaosSystem

QI Yan,LIU Liping

(Shenyang Ligong University,Shenyang 110159,China)

A double encryption algorithm of color image is proposed based on Standard map and Lorenz chaos system. Standard map was used to scramble the pixel position by its nonlinear feature. Lorenz chaos system was combined with R,G,B components of color image to diffuse pixels of image based on Lorenz′s 3D feature. The double encryption is composed by scrambling and diffusing,which overcomes the weakness of single encryption in poor security. Experimental and analysis results prove that the proposed algorithm has higher security and encryption performance.

chaos system;image encryption;standard map;Lorenz system

2013-12-24

辽宁省教育厅科学研究项目(L2011037)

祁燕(1978—)，女，副教授，研究方向：图像处理，计算机图形学和虚拟现实技术.

1003-1251(2014)04-0040-08

TP391

A

马金发)