随机相位对一类Bonhoeffer-Van der pol系统的影响

刘 红，张 宇

(1. 哈尔滨金融学院 基础部，哈尔滨 150001；2. 哈尔滨工业大学 理学院数学系，哈尔滨 150001)

近年来，混沌控制及其理论在国内外得到了迅速的发展，它在物理、医学、工程等方向上的应用已经成为一个热点话题.自从Ott, Grebogi和Yorke提出混沌控制的方法以来[1-3]，混沌控制方法就不断地被提出和改进，而这些混沌控制方法一般分为反馈控制和非反馈控制这两种类型，其中反馈控制是指将不稳定的周期轨道最终稳定到某个具体稳定的周期轨道上，非反馈控制是指利用所给的参数激励或外部激励来实现对系统的控制[4].之后，随着研究的不断深入，Ramesh和Narayanan实现了在服从均匀分布噪声背景下对混沌系统的控制[5]，Wei和Leng讨论了在白噪声背景下Duffing振子的混沌运动[6]，Liu等人研究了有界噪声对Duffing系统动力学行为的影响[7]，Qu和Hu等人利用弱谐和激励来研究非自治系统的混沌控制，尤其是在弱谐和激励下实现了随机相位对非自治系统的混沌控制[8]，Lei和Xu等人将随机相位应用到一类复Duffing系统中，从而实现系统的混沌控制[9-10].

混沌控制作为混沌研究的一个新阶段，已经呈现了广阔的发展前景.然而在一些实际的问题中，人们发现确定性的动力系统常常受到随机激励的影响，也就是小噪声的扰动，随着随机混沌控制这一方法的提出，利用随机激励对系统进行混沌控制已经受到各界的广泛关注.噪声在实际工程中广泛存在，因此研究噪声对系统的扰动产生的影响，不论在理论上还是在实际的应用中都具有普遍的意义.随机控制主要包括随机参数控制，随机力控制和随机相位控制这三种控制方法，本文主要研究噪声作为随机相位对系统进行混沌控制.

1 Bon hoeffer-Van der pol系统的混沌动力学行为

Bonhoeffer-Van der Pol振子是生物学、物理学、机械工程学中的一个重要系统，它是用来描述电刺激在神经细胞膜上传播的一个二维模型，简称为BVP系统[11].它是生物学中著名Hodgkin-Huxley模型的一种简单形式，和Van der Pol振子相比较，BVP振子有特殊的分叉结构，带有感应器的电阻是BVP振子的一个组成部分.Rabinovitch证实了在控制动力学行为方面，BVP振子比Van der Pol振子更有优势，这是因为在BVP振子中由于电阻的存在，可以诱导次临界的Andronov-Hopf分叉发生[12].它的应用渗透到各个领域，不论是在机械工程领域里，还是在通信工程领域中，Bonhoeffer-Van der Pol系统的特性都得到很好的发展.

Bonhoeffer-Van der pol模型的动力学方程为：

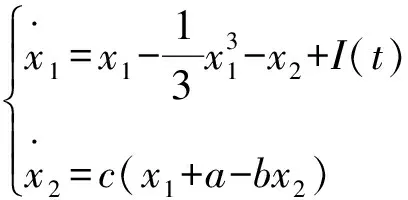
(1)

其中

I(t)=A0+A2cos(ωt)

在神经细胞学的应用中，x1表示神经细胞膜上的电势，x2表示折射率，I(t)是输入电流，a，b，c是常数，分别代表细胞膜的半径，不固定的电阻率和温度因数.

方程(1)可以写成：

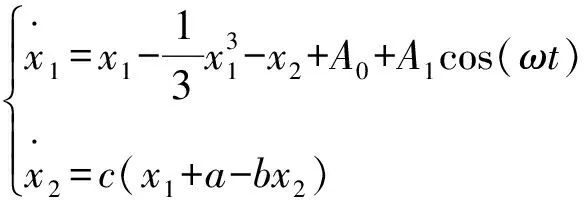
(2)

系统方程(2)的线性化方程为：

(3)

计算系统的最大Lyapunov指数为：

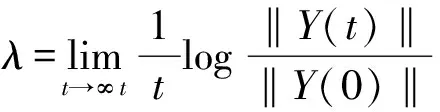
(4)

其中

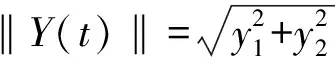
(5)

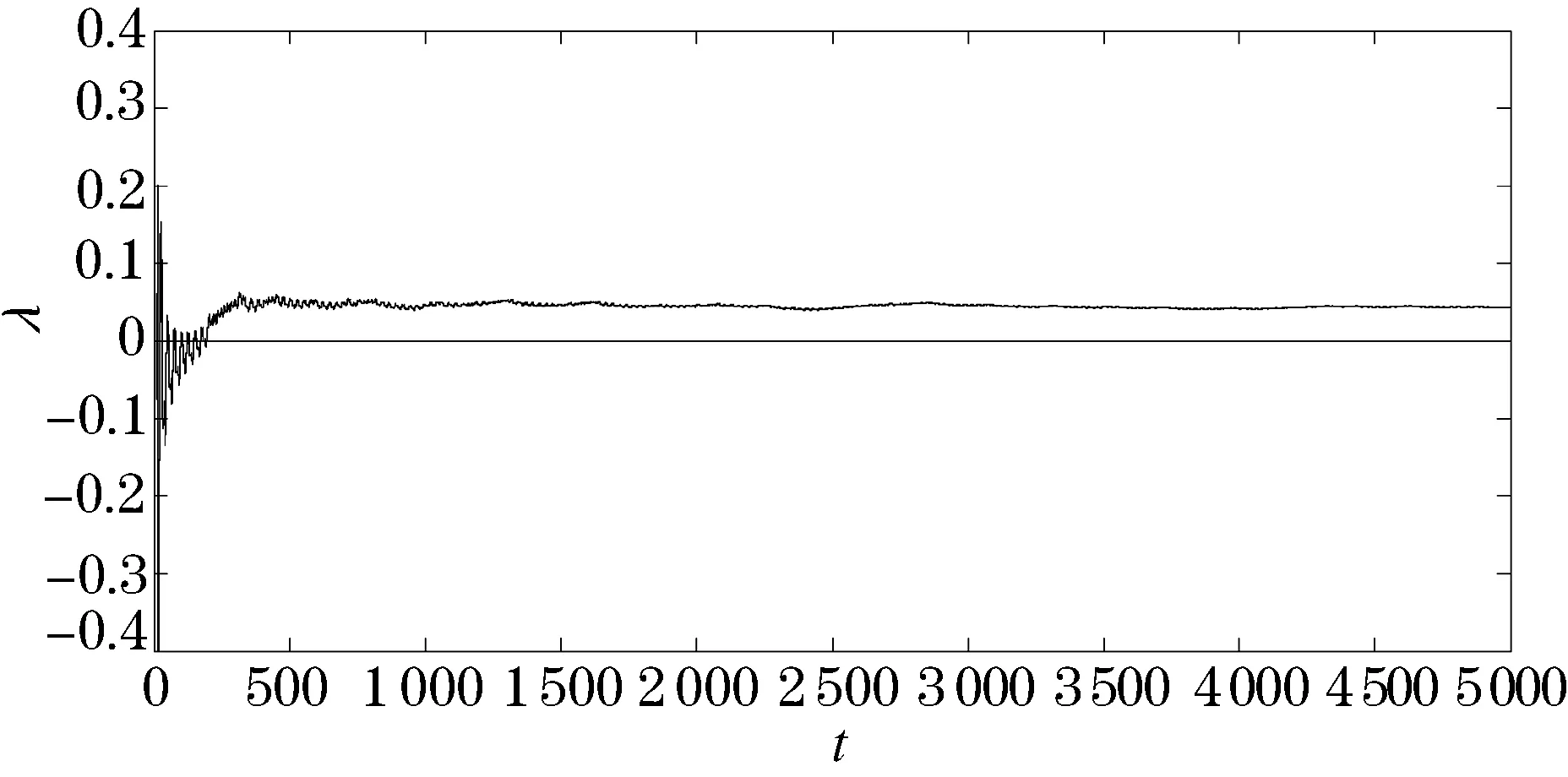
图1 最大Lyapunov指数随时间变化图

从图1中可以看出，最大Lyapunov指数λ值在开始的一段时间里在零点处上下波动，随着时间的变化，最大Lyapunov指数值始终大于0,系统出现了混沌现象.

为了进一步证实上述结论，做出Poincaré 截面

令

θ∶R1→S1

t→θ(t)=wt,mod 2π

(6)

方程(2)可以写成

(7)

定义截面为：

∑θ0={(x,θ)∈Rn×S1|θ=θ0∈(0,2π]}

(8)

做出系统的Poincaré 截面，如图2所示.

从图2中可以看到，Poincaré 截面上有成片的密集点，说明存在混沌吸引子，可知系统是混沌的.

我们随后做出系统的相图和时间历程图来证实结论的正确性，分别如图3、4所示.

从相图中可以看出，系统的相轨迹很混乱，没有一定的规律；从时间历程图中同样可以看出，时间历程不规则.通过对图像的分析，可知BVP系统在一定的参数范围内和初始条件下是混沌的.

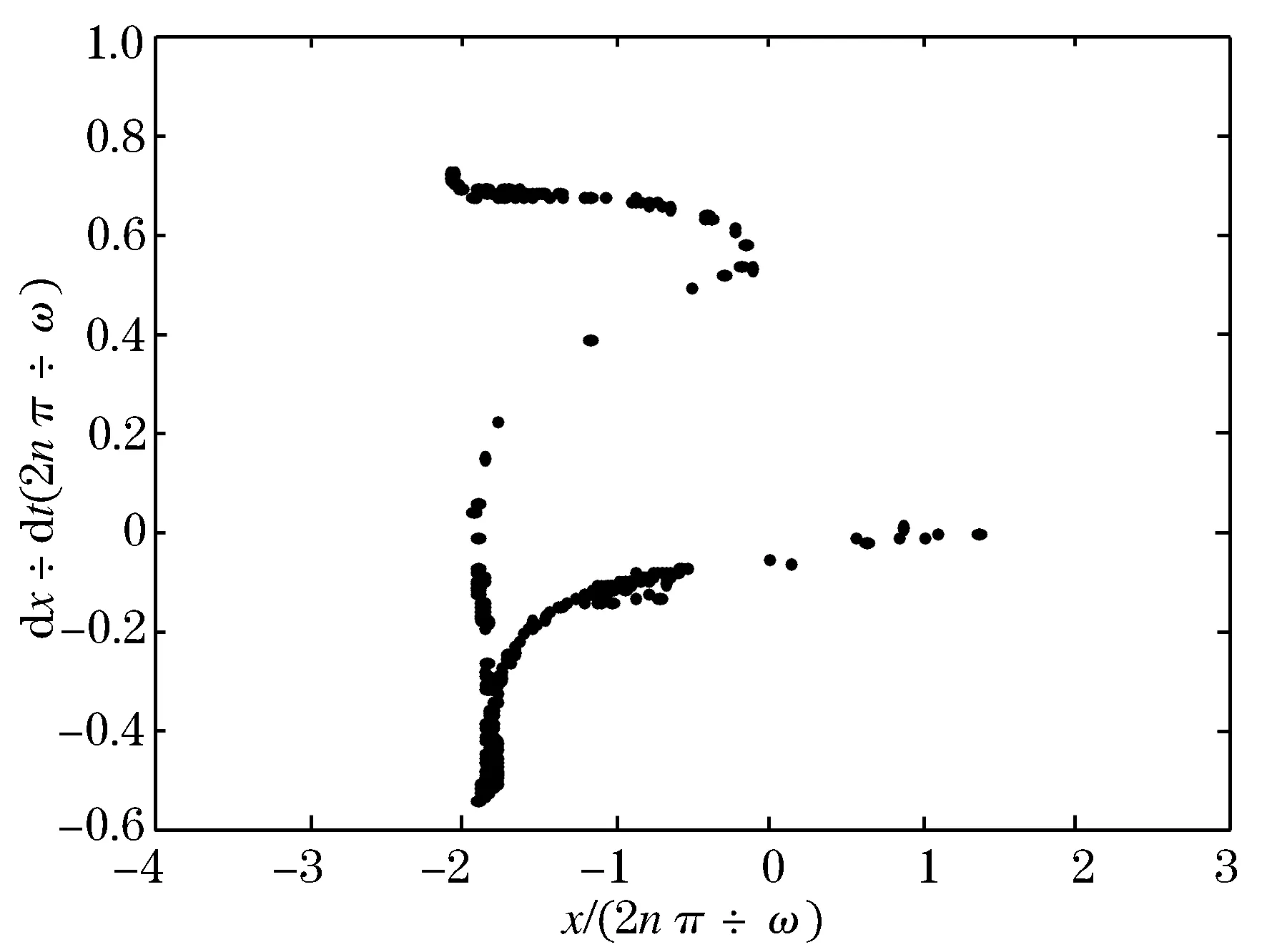
图2 Poincaré截面

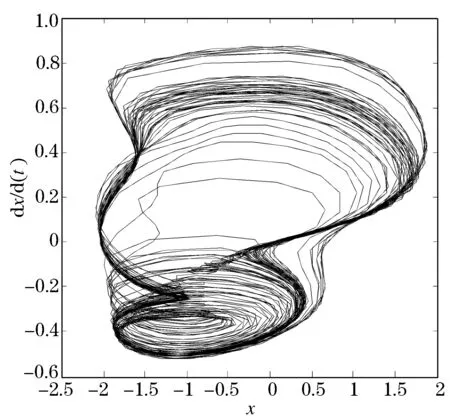
图3 相图

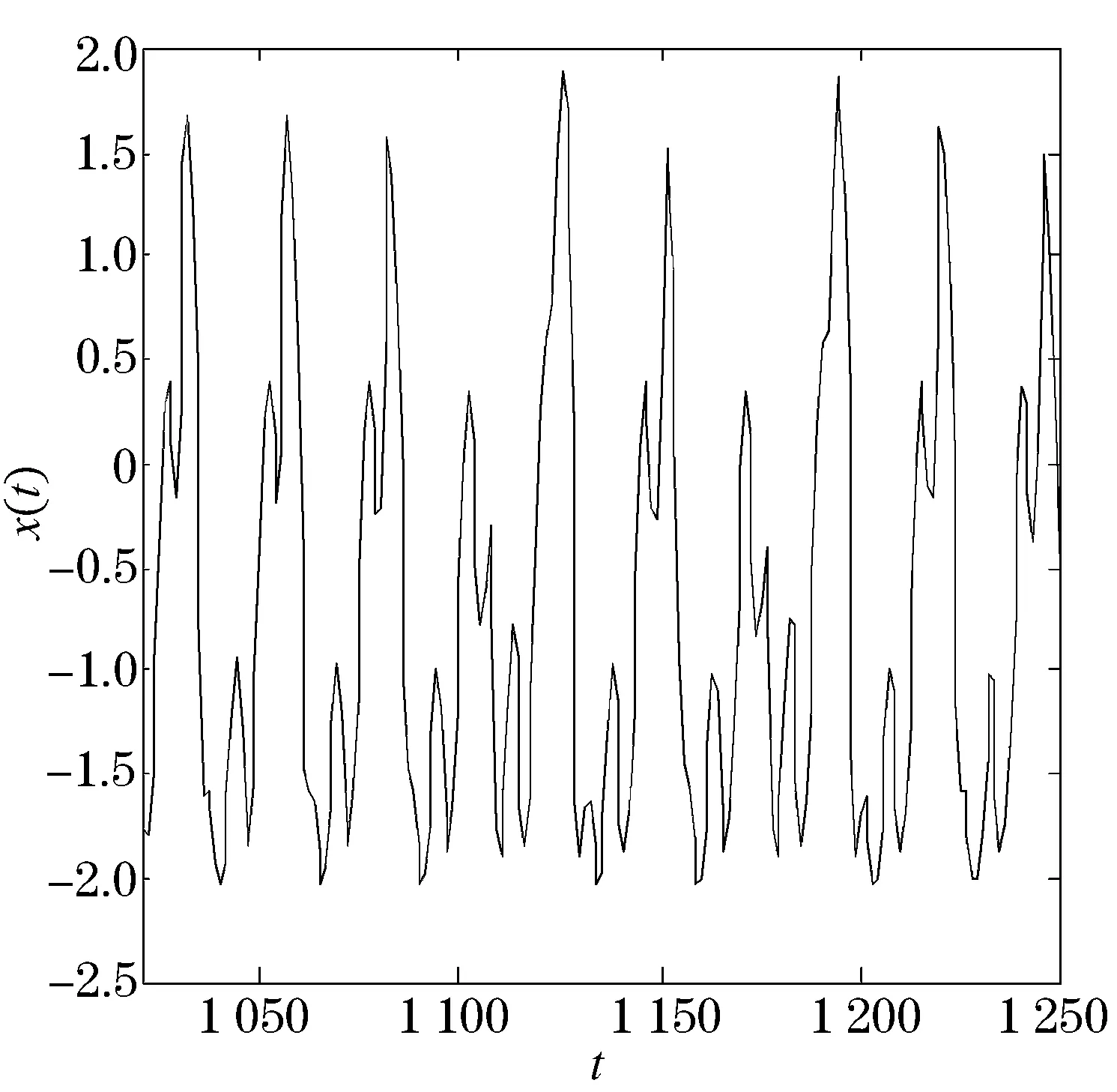
图4 时间历程图

2 Bonhoeffer-Van der pol系统的混沌控制

方程(2)加入随机相位后变成：

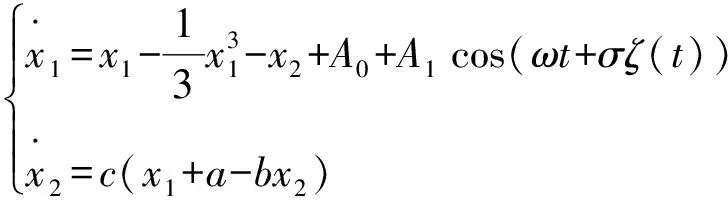
(9)

这里ζ(t)为标准的Gauss白噪声，σ表示噪声强度，其中ζ(t)满足：Eζ(t)=0，Eζ(t)ζ(t+τ)=δ(τ)，其中δ(τ)为Dirac-Delta函数.

相应的线性化方程为

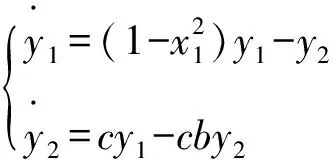
(10)

令

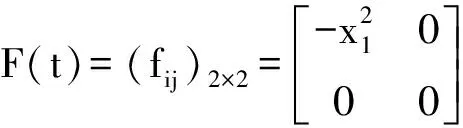
则有

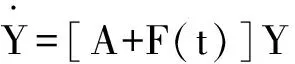
(11)

假设F(t)是遍历的，且有E[‖A+F(t)‖]<∞，由Oseledec多遍历性定理[13], ∃λ1,λ2和两个随机子空间E1,E2，其中，E1,E2满足：E1⨁E2=Uδ(0)⊂R2，其中Uδ(0)代表0点的邻域，则有

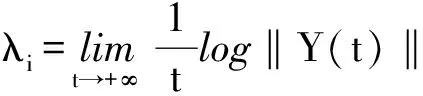
Y0∈Ei{0},i=1,2

这里

(12)

则λi(i=1,2)定义为Lyapunov指数.如果有

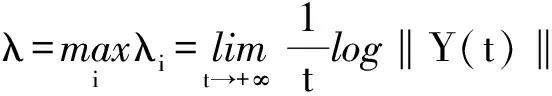
(13)

则λ被定义为系统的最大Lyapunov指数.

运用Wedig[14]引入的Khasminskii球面坐标变换[15]可得到最大Lyapunov指数的计算方法如下：

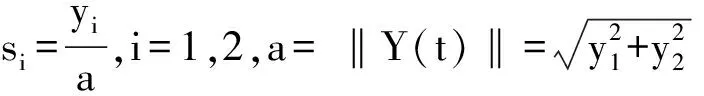
(14)

则有

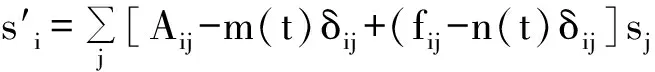
(15)

其中

且有

a′=[m(t)+n(t)]a

(16)

系统的最大Lyapunov指数为

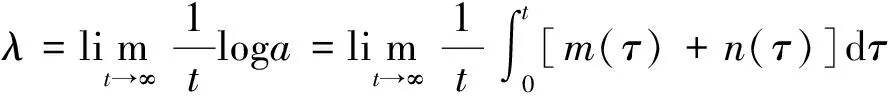
(17)

在实际的计算过程中，设步长为Δt，则式(17)右端可化为

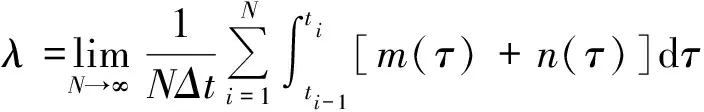
(18)

结合式(14)～(18)，对方程(9)和(10)求解，可以得到系统的最大Lyapunov指数.取上一节中相同的参数值和初始条件，经过多次数值模拟，得到系统平均最大Lyapunov指数随噪声强度σ的变化图1～5.

从图5可知，系统在σ=0时是混沌的，随着噪声强度σ的不断增加，当增加到一个临界值σc=0.05时，这时平均最大Lyapunov指数值λ由正变为负，表示系统的混沌现象变为了稳定的周期现象，之后σ的变化对平均最大Lyapunov指数的符号影响不大，这表明，在σ>σc=0.05这个范围内，成功地抑制了系统的混沌行为.接下来，我们做出系统的Poincaré 截面来证实上述的结论.

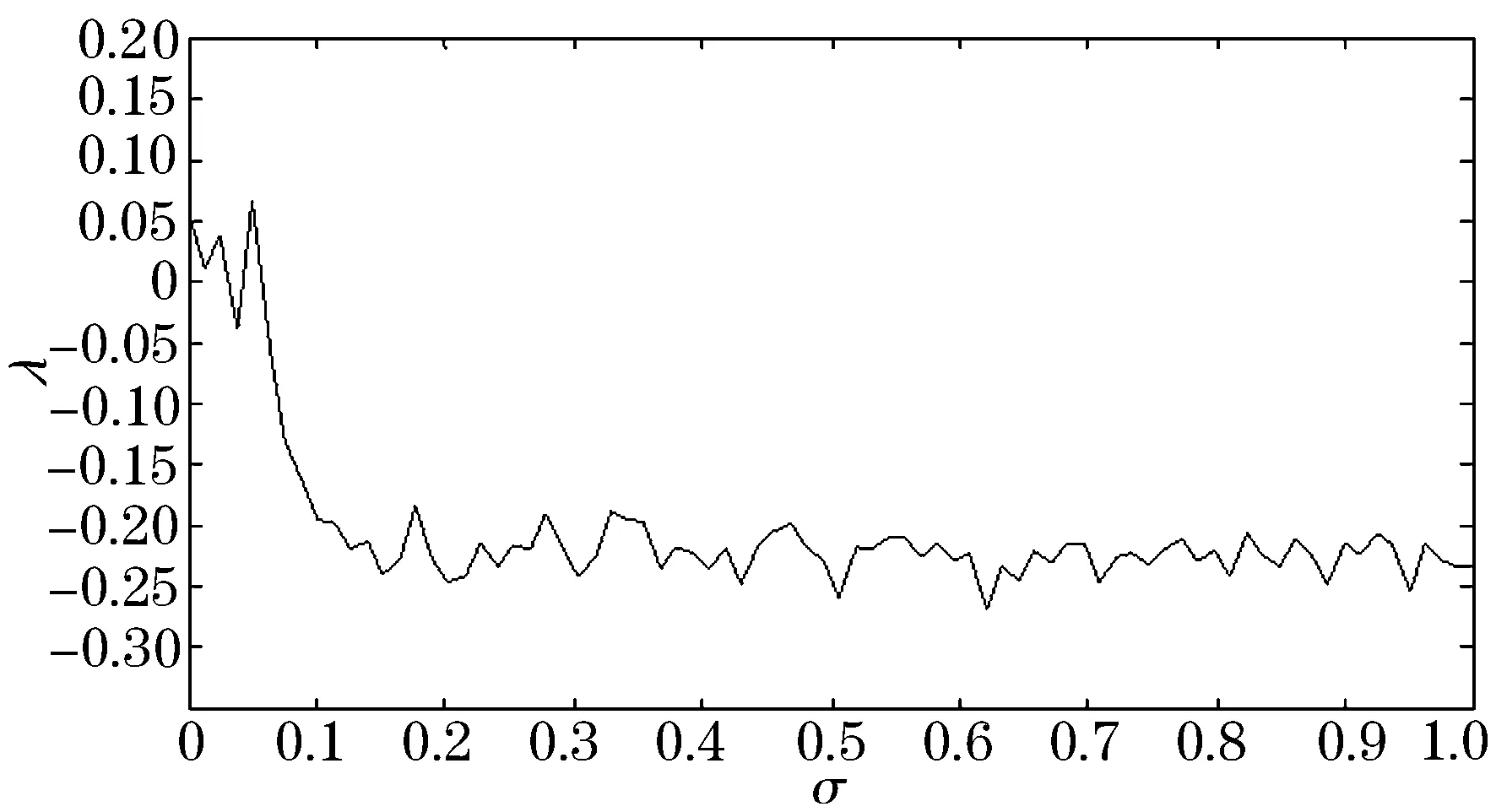
图5 平均最大Lyapunov指数随噪声强度变化的曲线图

令Poincaré 截面为

∑→∑,∑{(x(t),x(t))|t=0,2π/Ω,4π/Ω,…}⊆R2,

利用四阶Runge-Kutta法对微分方程(9)进行求解，在迭代一个周期T=2π/ω的时间内绘制一个点，删除最初200个点后，用剩下的200个迭代点来绘制系统的Poincaré 截面，当噪声强度σ=0.3时如图6所示.

从图6中可以看出，系统有稳定的吸引子，说明系统的混沌行为受到了控制.在相同的噪声强度下，做出系统的相图和时间历程图，分别如图7、8所示.

分析可知，系统的相轨迹从原来杂乱无章的曲线变成一个规则的圆点，时间历程图也呈规则状态.总之，通过这些图形的比对和分析，说明了利用Guass白噪声作为随机相位实现了BVP系统的混沌控制，系统从混沌状态转变为稳定状态.

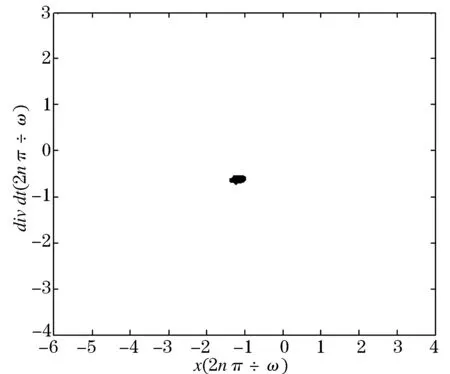
图6 σ=0.3时Poincaré 截面

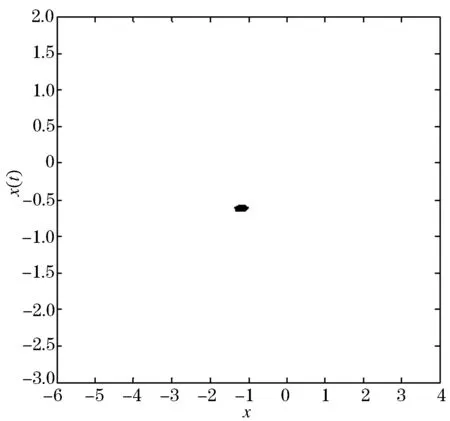
图7 σ=0.3时相图

图8 σ=0.1时时间遍历图

3 结 语

本文研究了Bonhoeffer-Van der pol系统的随机混沌控制，在给定的参数范围内，通过对系统的最大Lyapunov指数图的分析，基本可以判断系统是混沌的.为了能抑制混沌的产生，介绍了利用Guass白噪声作为随机相位对系统进行干扰，利用Matlab程序做出干扰后的最大Lyapunov指数图，通过对比分析，可知在一定的噪声强度下，系统的混沌行为得到了抑制.

参考文献：

[1] OTT E, GREBOGI C, YORK J A. Controlling chaos [J]. Physical Review Letters, 1990, 64(11): 1196-1999.

[2] SHINBROT T, OTT E, GREBOGI C. Using small perturbations to control chaos [J]. Nature, 1993, 363(3): 411-417.

[3] SHINBROT T, OTT E, GREBOGI C. Using chaos to direct trajectories [J]. Physical Review Letters, 1990, 3(65): 3215-3218.

[4] 李 爽, 徐 伟, 李瑞红. 利用随机相位实现Duffing系统的混沌控制[J]. 物理学报, 2006, 55(3): 1049-1054.

[5] RAMESH M, NARAYANAN S. Chaos control by non-feedback methods in the presence of noise [J]. Chaos, Solitons & Fractals, 1999, 6(10): 1473-1489.

[6] WEI J G, LENG G. Lyapunov exponent and chaos of duffing’s equation perturbed by white noise [J]. Applied Mathematics and Computation, 1997, 6(88)：77-93.

[7] LIU W Y, ZHU W Q, HUANG Z L. Effect of bounded noise on chaotic motion of a duffing oscillator under parametric excitation [J]. Chaos, Solitons&Fractals, 2001, 3(12): 527-537.

[8] QU Z, HU G. Phase effect in tamping non-autonomous chaos by weak harmonic perturbations [J]. Physical Review Letters, 1995, 74(6): 1736-1739.

[9] LEI Y M, XU W, XU Y. Chaos control by harmonic excitation with proper random phase [J]. Chaos, Solitons & Fractals. 2004, 21(3): 1175-1181.

[10] XU Y, XU W. Suppressing chaos of a complex duffing’s system using a random phase [J]. Chaos, Solitons&Fractals, 2005, 23(3): 265-273.

[11] 张 莹, 徐 伟, 孙晓娟. 随机Bonhonffer-Van der Pol 系统的随机混沌控制[J]. 物理学报, 2007, 56(10): 5665-5672.

[12] FREIRE J G. Stern-brocot trees in cascades of mixed-mode oscillations and canards in the extended Bonhoeffer-Van der pol and the fithugh-nagumo models of excitable systems [J]. Physical Review Letters, 2011, 375(7): 1097-1103.

[13] OSELEDEC Y I. A multiplicative ergodic theorem: Lyapunov characteristic number for dynamical system [J]. Transactions of the Moscow Mathematical Society, 1968, 19(6): 197-231.

[14] WEDIG W V. Dynamic stability of beams under axial forces: Lyapunov exponents for general fluctuating loads [J]. Earthquake Engineering & Structural Dynamics, 1990, 21(3): 141-148.

[15] KHASMINSKII R Z. Necessary and sufficient conditions for the asymptotic stability of linear stochastic systems [J]. Theory of Probability and its Applications, 1967, 12(2): 44-147.

[16] 许 楠，刘丽杰，徐耀群.高斯激励混沌神经元系统及其应用[J]. 哈尔滨商业大学学报：自然科学版，2014，30(5)：599-603.