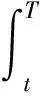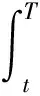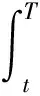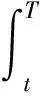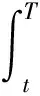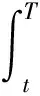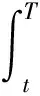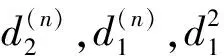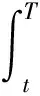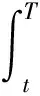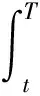分数跳-扩散O-U过程下幂型期权定价
2014-09-14符双,薛红
符 双,薛 红
(西安工程大学 理学院,西安 710048)
期权定价问题是金融数学和金融工程学的核心问题之一.文献[1]假设股票价格服从布朗运动,得到了著名的Black-Scholes公式.文献[2]首次提出期权定价的保险精算方法,将期权定价问题转化为等价的公平保费确定问题,它不仅对于无套利、均衡、完备的市场有效,且对于有套利、非均衡、不完备的市场也有效.文献[3]利用保险精算方法得到了欧式期权的定价公式.
近年来,国际金融市场涌现了大量由标准期权变化、组合、派生而来的新品种,即新型期权.幂型期权是新型期权中的一种,它允许持有人得到一个标准期权的损益,但标的资产的价值被提高到它的q次幂,它与标准欧式期权的区别在于在期权到期日,当期权处于实值状态时,标准欧式看涨(跌)期权的支付函数为标的资产价格的线性函数,而幂型期权的支付函数为标的资产价格幂函数的线性函数.目前已有不少学者对幂型期权的定价进行了研究,文献[4]研究了几何布朗运动下幂型期权的定价问题.由于股票价格对过去价格具有依赖性,而分数布朗运动具有的长程依赖性和自相似性,弥补了几何布朗运动描述标的资产的不足,一些学者考虑用分数布朗运动刻画股票价格的变化[5-7],在现实资本市场中,因突发事件的影响,股票价格会发生跳变.许多学者用Possion过程和分数布朗运动驱动的随机微分方程来描述股票价格的变化[8-10].研究发现,分数跳-扩散Ornstein-Uhlenback 模型能更好地描述股票价格的运动变化,一些学者讨论了分数跳-扩散Ornstein-Uhlenback 模型的欧式期权和欧式双向期权的定价问题[11-12].
本文在文献[11-12]基础上,假定股票价格服从分数跳-扩散Ornstein-Uhlenback过程,且无风险利率和股票波动率均为时间的确定性函数,利用保险精算方法,讨论幂型期权的定价问题.
1 金融市场数学模型
假设金融市场中,有两类可交易的资产:一种是无风险资产(如债券),其价格过程记为Pt,t≥0,满足如下常微分方程
dPt=r(t)Ptdt,
(1)
其中:r(t)为时刻t的函数,称其为无风险利率.另一种是风险资产(如股票),其价格过程记为St,t≥0,它满足如下随机微分方程
dSt=St[μ(t)-αlnSt-λθ)dt+σ(t)dBH(t)+dJ(t)],
(2)
其中:μ(t)为股票的预期收益率,σ(t)为股票的波动率,μ(t)和σ(t)均为确定性的函数,α>0且为常数.{BH(t),t≥0}是定义在概率空间(Ω,F,P)上Hurst参数为H(0 {N(t),t≥0}表示强度为λ的泊松过程,Ui表示第i次跳跃幅度(无跳跃发生时U0=0),{Ui,i≥0}为一列独立同分布的随机变量,并且θ=E[Ui],Ui>-1(i=1,2…).假定{BH(t),t≥0},{N(t),t≥0}和{Ui,i≥0}相互独立.{*t≥0}是由{BH(t),t≥0},{N(t),t≥0}和{Ui,i=1,2,…}生成的σ-代数流. 定理1 随机微分方程(2)的解为 证明假定[0-,t]之间没有跳发生,根据分数型Ito公式及(2)可知 那么 假定只在时刻T1∈[0,t] 发生一次跳, 则 由式(2)有 当n→∞时,可得 ST1-ST1-=ST1-U1. 所以 σ(τ)dBH(τ)]}. 当跳的次数服从Possion过程时,则有 定理证毕. 证明 由于 从而完成定理证明. 定义2 幂型期权的保险精算价值定义为:当期权被执行时,在[t,T]内标的资产q的次幂的折现值与敲定价格的折现值之差,在股票价格实际分布的概率测度下的数学期望值.资产折现值的计算方法按如下计算:风险资产(如股票)按期望收益率折现,无风险资产(如债券或银行存款)按无风险利率折现.用公式表示为 其中ST为标的资产的价格,K为敲定价格,T为到期日,且 ds})q}, C(t,K,T)和P(t,K,T)分别表示到期日为T,敲定价格为K,在时刻t的欧式幂型看涨期权和看跌期权的价值. 其中Φ(·)为标准正态分布的分布函数,且 证明由定理1和定理2可知 从而 从而 注1:当a→0时,可得分数跳-扩散环境下欧式幂型期权的价格.特别地,当σ为常数时,即为文献[10]的相应结果. 注2:当λ=0,Ui=0,i=0,1,2,…时,可得分数O-U过程下的欧式幂型期权的价格.特别地,当a→0,σ为常数时,即为文献[7]的相应结果. 参考文献: [1] BLACK F, SCHOLES M. The pricing of options and corporate liabilities [J]. Journal of Political Economy, 1973, 81: 637-659. [2] BLADT M, RYDBERG H T. An actuarial approach to option pricing under the physical measure and without Market assumptions [J]. Insurance: Mathematics and Economics, 1998, 22(1): 65-73. [3] 闫海峰, 刘三阳. 广义Black-Scholes模型期权定价新方法—保险精算方法[J]. 应用力学和数学, 2003, 24(7): 730-738. [4] 陈万义. 幂型支付的欧式期权定价公式[J]. 数学的实践与认识, 2005, 35(6): 52-55. [5] 赵佃立. 分数布朗运动环境下欧式幂型期权的定价[J]. 经济数学, 2007, 24(1): 22-24. [6] 唐 奎, 杜 燕, 张志恒. 分数几何布朗运动环境下幂型支付期权的保险精算定价[J]. 重庆理工大学学报:社会科学版, 2010, 24(6): 33-37. [7] 刘海媛, 周圣武, 索新丽. 标的资产价格服从分数布朗运动的几种新型期权定价[J]. 数学的实践与认识, 2008, 38(15): 54-59. [8] 董志英. 股票价格服从分形跳-扩散过程的欧式幂型期权定价[J]. 乐山师范学院学报, 2009, 24(5): 19-20. [9] 胡素敏, 胡电喜. 基于分数跳扩散过程的幂期权定价[J]. 湖南师范大学自然科学学报, 2012, 35(6): 16-17. [10] 薛 红, 孙玉东. 分数跳-扩散环境下几种新型期权定价模型[J]. 数学的实践与认识, 2012, 42(24): 136-140. [11] 孙玉东, 薛 红. 分数跳-扩散环境下欧式期权定价的Ornstein-Uhlenbeck模型[ J]. 经济数学, 2009, 26( 3): 23-28. [12] 马惠馨, 薛 红, 杨 珊. 分数跳-扩散环境下欧式双向期权定价的Ornstein-Uhlenbeck模型[J]. 西安工程大学学报, 2011, 25(2): 261-265.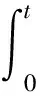
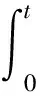
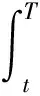
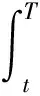
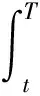
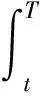
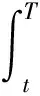
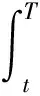
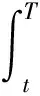
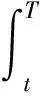
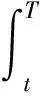
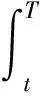
2 欧式幂型期权的定价