加权有穷自动机的代数性质*

2014-09-13张丽霞

计算机工程与科学 2014年11期

关键词：半环幂级数自动机

张丽霞

(安庆师范学院数学与计算科学学院,安徽安庆 246013)

加权有穷自动机的代数性质*

张丽霞

(安庆师范学院数学与计算科学学院,安徽安庆 246013)

在加权有穷自动机理论基础上，利用强同态的概念，证明两个加权有穷自动机在计算能力上是等价的，并在加权有穷自动机的状态集上建立一种等价关系，得到加权有穷自动机的商自动机，证明加权有穷自动机与其商自动机在计算能力上也是等价的。并通过引入加权有穷自动机的可交换性、分离性、(强)连通性及层的概念，讨论在(强)同态的条件下，两个加权有限状态机之间的可交换性、分离性、(强)连通性及层的关系。

形式幂级数；加权有穷自动机；同态；强连通

1 引言

在计算机科学中，自动机作为计算过程的动态数学模型，用来研究计算机的体系结构、逻辑操作、程序设计乃至计算复杂性理论[1～5]。1961年，Schützenberger M P[6]首先提出了加权自动机的概念，并提出了半环上的形式幂级数的概念，证明了Kleene-Schützenberger 定理，即加权有穷自动机所识别的形式幂级数和有理幂级数是一致的。随后，又有很多学者在这一领域作出了进一步有意义的工作[7～12]。目前，加权自动机在模式识别、模型检测、数字图像压缩算法等领域取得了广泛的应用[13～15]。由于 Successor 和Source 算子是自动机理论中的重要工具之一，Kuroki N、Tiwari S P，Srivastava A K等[16～21]利用 Successor 和 Source算子研究了模糊有穷自动机(强)连通性、分离性、交换等性质，并给出了模糊自动机一些结构刻画。本文将在半环的结构上，研究加权有穷自动机的同态和强同态及其性质，并在加权有穷自动机的状态集上建立一种等价关系，从而得到加权有穷自动机的商自动机。进一步，利用(强)同态的概念，讨论了两个加权有限状态机之间的可交换性、分离性、(强)连通性及层的关系。

2 基本概念与符号

首先，我们引入一些必要的概念与记号，详细请参考文献[11,12,17,20]。

集合S是带有两个二元运算⊕、⊗和两个特殊元素0、1的集合，并且满足:

(1)(S,⊕,0)是交换幺半群;

(2)(S,⊗,1)是幺半群;

(3) 对任意a,b,c∈S，有a⊗(b⊕c)=a⊗b⊕a⊗c，(b⊕c)⊗a=b⊗a⊕c⊗a;

(4) 对任意a∈S，有0⊗a=a⊗0=0。

称(S,⊕,⊗,0,1)为半环。为了方便讨论，本文简记S。如果对任意a,b∈S，都有ab=ba，则称半环S为交换半环。半环理论作为具有广泛应用背景的代数系统在计算机理论科学中具有特殊性及重要性。特别在经典的形式语言理论中，最重要的半环是Boolean半环S={0,1}。

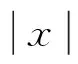
设S是一个半环，称Σ*到S的映射A为形式幂级数。对任意x∈Σ*，A在x处的值记为(A,x)，并记A为:

称A为变量在Σ中的形式幂级数，其中(A,x)为此形式幂级数的系数。所有形式幂级数组成的集合记为S≼Σ*。

设A,B∈S≼Σ*，若对任意x∈Σ*，有A(x)=B(x)，则称A等于B，记作A=B。

定义1[11]设S是半环，加权有穷自动机(简记为WFA)(WeightedFiniteAutomata)是五元组W=(Q,Σ,δ,I,F)，其中，Q为有限状态集合，Σ为有限输入字符集，I:Q→S与F:Q→S分别代表权值初始状态与权值接受状态，而δ:Q×Σ×Q→S为权值转移函数。

更进一步，若对q∈Q,x∈∑，存在唯一的p∈Q使得δ(q,x,p)=1，而对其余的r∈Q，都有δ(q,x,r)=0，并且存在唯一的q′∈Q使得I(q′)=1，则得到通常的确定型加权有穷自动机的概念。

转移函数δ可以扩张到Q×∑*×Q上，即δ*:Q×∑*×Q→S满足如下条件:

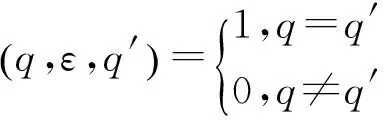
(2) 对输入序列x=x1x2…xk∈∑*,k≥1,则:

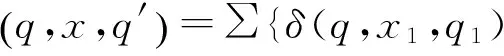
根据上述定义，易验证下列等式成立:

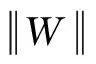
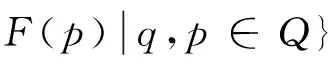
另外，对任意A∈S≼Σ*，若存在一个WFAW使A恰为W接受的形式幂级数，则称A为Σ上的正则幂级数。

为了对不同的加权有穷自动机进行比较，下面引入加权有穷自动机之间同态和强同态的概念。

定义3[11]设S是半环，W=(Q,Σ,δ,I,F)和W1=(Q1,Σ,δ1,I1,F1)是两个WFA。设映射φ:Q→Q1，对任意q,q′∈Q，x∈Σ，若满足下列条件：

I(q)≤I1(φ(q))，F(q)≤F1(φ(q))，δ(q,x,q′)≤δ1(φ(q),x,φ(q′))

则称φ为同态映射。

进一步，若φ满足:

F1(φ(q))=F(q)。

则称φ为强同态。若φ是强同态且同时是双射，则称φ为同构。

Successor算子是自动机理论中的重要工具之一。在文献[22]中，Zamir B首先提出了Successor算子的概念，并利用Successor算子研究了有穷自动机一些特有的性质。近年来，Tiwar S P等[19～21]在模糊集合的理论基础上，利用Successor算子给出了模糊有穷自动机一些结构刻画。本文将利用Successor算子来定义加权有穷自动机的交换性、强连通性、分离性等概念，利用这些概念来讨论加权有穷自动机的一些特性。

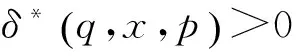
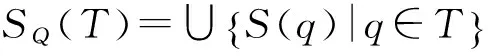
定义5设S是半环，W=(Q,Σ,δ,I,F)是一个WFA，则:

(1) 对任意p,q∈Q，若q∈S(p)当且仅当p∈S(q)，则称W满足交换性。

(2) 对任意p,q∈Q，都有p∈S(q)，则称W是强连通的。

(3)T⊆Q，δ是T×Σ×T的一个加权子集。若满足以下两个条件:

①δ|T×Σ×T=η;

②SQ(T)⊆T。

则称N=(T,Σ,η,I|T,F|T)是W的子加权有穷自动机。若T≠Q且T≠∅，则称N是W的真子加权有穷自动机。

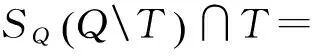
定义7设S是半环，W=(Q,Σ,δ,I,F)是一个WFA。如果W是没有可分离的真子加权有穷自动机，则称W是连通的。

3 主要结果

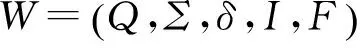
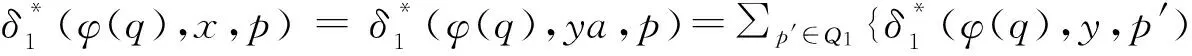
∑p′∈Q1{∑s∈Q{δ*(q,y,s)|φ(s) =p′} ⊗∑p∈Q1{δ*(s,u,r)|φ(r)=p}}=

∑p′∈Q1{∑r,s∈Q{δ*(q,y,s)|φ(s) =p′} ⊗{δ*(s,u,r)|φ(r)=p}}=

∑r∈Q{δ*(q,yu,r)|φ(r)=p}

充分性。因为φ是单射，故对任意q,r∈Q，且x∈Σ*，有：

因此，φ是强同态。

□

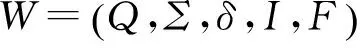
证明对任意x∈Σ*，有:

□

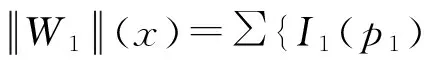
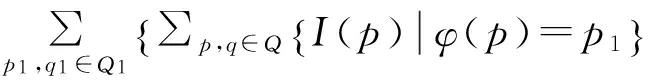
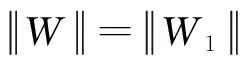
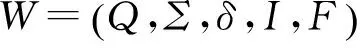
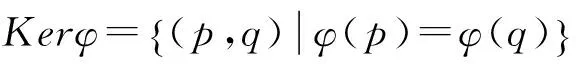
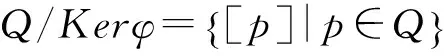
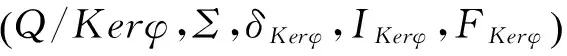
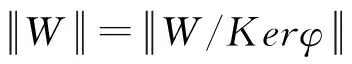
证明对任意x∈Σ*，有：

□

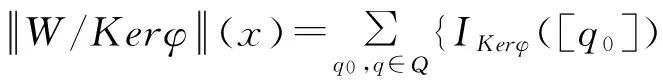
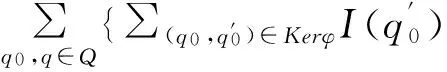
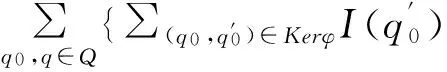
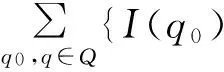
定理3说明了加权有穷自动机与其商自动机在计算能力上是等价的，从而实现了加权有穷自动机的状态极小化。

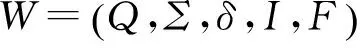
引理1[19]设S是半环，W=(Q,Σ,δ,I,F)是一个WFA，则W是强连通的充分条件是W没有真子加权有穷自动机。

定理5设S是半环，W=(Q,Σ,δ,I,F)是一个WFA，则：

(1) 若W是强连通的当且仅当W是连通的且满足交换性;

(2) 若W是强连通的，则Q自身为W的一个层。

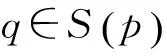
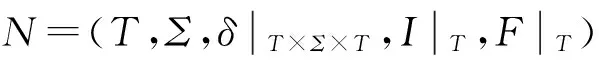
(2) 显然，若W=(Q,Σ,δ,I,F)是强连通的当且仅当S(q)=Q，q∈Q，根据可分离的定义，Q为W的一个层。

□

定理6设S是半环，W=(Q,Σ,δ,I,F)是一个WFA，则W必有一个强连通的子加权有穷自动机。

□

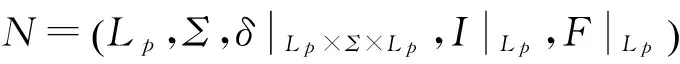
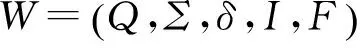
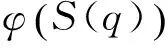
(2) 若p∈Q，Lp为W的一个层，则φ(Lp1)为W1的一个层。

证明(1) 根据加权有穷自动机同态的定义可得。

□

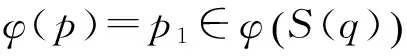
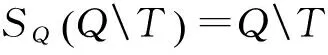
根据引理2，我们有如下结论。

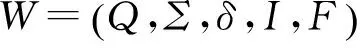
4 结束语

本文在半环的结构上，利用强同态的概念，证明了两个加权有穷自动机在计算能力上是等价的，并在加权有穷自动机的状态集上建立了一种等价关系，得到了加权有穷自动机的商自动机，证明了加权有穷自动机与其商自动机在计算能力上也是等价的，从而实现了加权有穷自动机的状态极小化。此外，我们给出了加权有穷自动机的可交换性、分离性、(强)连通性及层的概念，讨论了在(强)同态的条件下，两个加权有限状态机之间的可交换性、分离性、(强)连通性及层的关系。这些研究结果进一步丰富了加权自动机的理论。

[1] Shannon C E, MeCary J. Automata studies[M]. Prineeton:Prineeton University Press, 1956.

[2] Hopcroft J E, Ullman J D. Introduction to automata theory, languages and computation[M]. New York:Addison-Wesley, 1979.

[3] Zadeh L A. Outline of a new approach to the analysis of complex systems and decision processes[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1973(1):28-44.

[4] Mordeson J N, Malik D S. Fuzzy and languages:Theory and applications[M]. Boca Paton:Chapman &Hall/CRC, 2002.

[5] Malik D S, Mordeson J N, Sen M K. On subsystems of a fuzzy finite state machines[J]. Fuzzy Sets and Systems,1994,68(2):83-92.

[6] Schützenberger M P. On the definition of a family of automata[J]. Information and Control,1961(4):245-270.

[7] Salomaa A, Soittola M. Automata theoretic aspects formal power series[M]. Berlin:Springer, 1978.

[8] Droste M,Kuich W,Vogler H.A Kleene theorem for weighted tree automata[J]. Theory of Computing Systems, 2005,38(1):1-38.

[9] Droste M, Gastin P. Weighted automata and weighted logics[J]. Theoretical Computer Science,2007,380(1-2):69-86.

[10] Berstel J, Reutenauer C. Noncommutative rational series with applications, encyclopedia of mathematics and its applications[M]. Cambridge:Cambridge University Press, 2010.

[11] Li Y M,Wang Q.The universal fuzzy automation[J].Fuzzy Sets and Systems,2014,249:27-48.

[12] Li Y M. Analysis of fuzzy systems[M].Beijing:Science Press,2005.(in Chinese)

[13] Ong G H, Kai Y. A binary partitioning approach to image compression using weighted finite automata for large images[J]. Computers & Mathematics with Applications, 2006, 51(11):1705-1714.

[14] Albert J, Kari J. Digital image compression[M]∥Handbook of Weighted Automata[M]. Berlin:Springer -Verlag,2009(Chapter11).

[15] Bouyer P. Weighted timed automata:Model-checking and games[J]. Electronic Notes in Theoretical Computer Science, 2006, 158(5):3-17.

[16] Kuroki N, Mordeson J N. Successor and source functions[J]. J Fuzzy Math, 1997(5):173-182.

[17] Srivastava, A K, Tiwari S P. A topology for fuzzy automata [C]∥Proc of AFSS’02, 2002:485-490.

[18] Srivastava A K , Tiwari S P. On another decomposition of fuzzy automata [J]. Journal of Uncertain Systems, 2011,5(1):33-37.

[19] Tiwari S P, Singh A K, Sharan S. Fuzzy automata based on lattice-order monoid and associated topology[J]. Journal of Uncertain Systems, 2012,6(1):51-55.

[20] Tiwari S P, Sharan S. Fuzzy automata based on lattice-ordered monoid with algebraic and topological aspects[J]. International Journal of Fuzzy and Information Engineering, 2012, 4(2):155-164.

[21] Tiwari S P,Yadav V K,Anupam K S.On algebraic study of fuzzy automata [J]. International Journal of Machine Learning and Cybernetics,doi:10.1007/s13042-014-0233-5.

[22] Zamir B. Introduction to the theory of automata[M]. Virginia:Reston Publishing Company, 1983.

附中文参考文献:

[12] 李永明. 模糊系统分析[M].北京:科学出版社,2005.

ZHANGLi-xia,born in 1984,MS,lecturer,her research interests include representation theory of algebras, and algebraic theory of automata.

Algebraicpropertiesofweightedfinitestateautomata

ZHANG Li-xia

(School of Mathematics and Computation,Anqing Normal University,Anqing 246013,China)

On the basis of the theory of weighted finite automata,we prove the computing equivalence between two weighted finite automatas under the strong homomorphism of weighted finite automatas, and obtain the quotient weighted automata by establishing the equivalence relation on the states of weighted finite automata.Based on the equivalence relation,the equivalence between weighted finite automata and its quotient automata is also proved.Specifically,the concepts such as commutability,separateness,(strong) connectedness properties and layers of weighted finite automata are introduced,and their relations in two different weighted finite automata are discussed under the homomorphism or strong homomorphism.

formal power series;weighted finite automata;homomorphism;strong connectedness

1007-130X(2014)11-2186-05

2014-07-10;

：2014-09-16

安庆师范学院青年科研基金项目(KJ201214)；安徽省优秀青年人才基金项目(2011SQRL097)

TP301

：A

10.3969/j.issn.1007-130X.2014.11.022