农产品生产商主导的分销网络博弈模型
2014-09-13刘晓华梁雪春
刘晓华,梁雪春
(南京工业大学 自动化与电气工程学院,江苏 南京 211816)
农产品生产商是农产品分销网络中最具敏感边际效益的群体,分销中心几乎垄断控制了分销网络生产环节以外的其他环节,例如流通存储、运输、店铺摊位、运行管理等,导致了农产品生产商的信息不对等,无法有效识别和分析农产品价格信息。市场调节的快速性及不对称性使得农产品生产商获取信息滞后,最终处于分销网络弱势的地位。农产品生产商利润的提高需要农产品分销网络各成员在市场链条中对其策略进行保护并做出博弈均衡[1]。
国内外很多文献研究博弈论及延期支付策略在分销网络中的应用:Erlebacher和Daskin[2-3]都从风险分担合作的角度分析了分销网络支付策略和博弈合作问题,Kazaz[4]从市场角度分析橄榄油的生产问题,并提出了生产支付决策方法,Inderfurth[5]在产量和需求均是均匀分布的前提下从支付决策的角度来分析产量和需求之间的博弈关系,并对各种博弈模型做了比较;Yang和Barueh[6-7]对库存策略、订货模型进行了研究,并得到生产商最优订货量和生产量的解析解;Chang和Liao[8-9]分析了在延期支付期限条件下易逝品的最优订货问题;朱文贵等[10-11]重点研究了延期支付策略等定价问题;赵菊和曾文瑛[12-13]则从博弈的角度研究了订货决策问题。
结合以上研究发现,延迟支付库存优化策略更能提高生产商利润,可以作为提高农产品生产商竞争力的库存优化策略。同时Stackelberg博弈是一种有效地解决博弈问题中信息不对等和不完全理性的决策理论,博弈过程中可以强行保护从方的利益和地位。农产品生产商为主导的stackelberg博弈模型将农产品生产商作为从方参与,农产品分销中心作为主方,可以进一步提高农产品生产商在分销网络中的竞争力,具有重要的理论和现实意义。
1 农产品分销网络各节点延期支付
利润模型
延期支付是一种商业信贷和资金投放的形式,它指生产商(卖方)给与分销商或零售商(买方)一定的贷款支付期限优惠。在买卖双方的合作中,延期支付库存优化策略可以促使农产品生产商获取更多的信息,对分销中心的状况有比较全面的了解,增强了其对分销中心的控制力和处理价格歧视行为的能力。同时,如果有违约情况发生,生产商处理库存的成本更低,减少了其成本损失。
生产商模型符号如下:pM为生产商单位农产品售价,s为单位运输费用,c为单位成本,e为单位时间产量,k为单位库存费用,T为订货周期(固定),IP为利息支付每单位时间每单位货币。农产品分销中心模型符号如下:pD为单位农产品售价,A为订货费用,IR为利息收入每单位时间每单位货币,h为分库存设施、库存管理及资金积压等费。其他参数:M为延期支付期限,I(t)为农产品分销中心t时刻库存,农产品分销中心单位时间需求D=a-bPD。
本文中农产品分销中心总的利润函数=销售利润-库存费用-订货费用-运输费用+延期支付收入。单位周期的订货量为Q=I(0)=DT,订货费用为A+sQ,销售利润为(pD-pM)Q;随着产品的销售分销中心的库存逐渐减少,库存满足dI(t)/dt=-D,0≤t≤T,得到I(t)=(T-t)D农产品分销中心的库存费用为

(1)
分销中心延期支付期限获得的利息:当M≥T时,分销中心在T时间内销售所有农产品,持有全部销售收入至M时刻才缴纳pMDT的货款; 当M (2) 农产品分销中心总利润函数π为 (3) 农产品生产商利润Φ=农产品销售利润-利息支出-农产品库存费用,其中销售利润为(pM-c)Q,生产商周期内支付产生的利息为MpMQIp;库存为eT,eT>Q;生产商的库存费用表达式为:k(eT-DT)。 Φ(pD,M)=(pM-c)Q-MpMQIP.-k(eT-DT) (4) 分销网络利润函数Π=分销中心利润+生产商利润,由式(2)~(4)可以得出:农产品分销网络库存成本Ψ=农产品分销中心库存成本+农产品生产商库存成本: (5) Stackelberg博弈的基本参量如下,信息载体有:农产品产量、库存水平、订货状态、需求预测、生产/发货计划、提前期、延迟;农产品生产商的行动是生产、销售、契约、质量保证,而分销中心的行动是: 订货、契约、质量保证; 农产品生产商和农产品分销中心的支付函数就是其分别的利润函数,其相应的战略就是最大化自己的利润函数。 Stackelberg博弈模型如下: 式中:x为从方决策参量,y为主方决策参量,函数F代表利益函数。 决策机制为:农产品生产商首先宣布,使它的利润函数达到最优的延迟支付期限,这一决策将影响后行动者农产品分销中心的利润,分销中心在这一前提下选取使自己利润最优的订货量。 农产品生产商预先估计到分销中心针对延期支付策略而产生的反应,确定最优延期支付期限:Q=DT=(a-bp)T,将PD1带入生产商利润模型可以得到 (pM-c-MpMIP+kT)-keT (6) c-kT=K3,得 Φ1(pD1,M)= (7) 对式(7)求导得到一阶和二阶函数为: 农产品分销中心根据生产商的延期支付策略制定出能使自身利润最大化的决策,结合D=a-bp,对式(3)进行一阶和二阶求导,得出分销中心利润函数π1(pD)和π2(PD)存在最大值,则农产品分销中心结合生产商的延期支付策略,其最优销售价为 (8) 农产品分销中心根据给定的延期支付期限M*和函数(8)得到最优的价格,根据Q=(a-bp)T及I(t)=(T-t)D得到最优的订货批量。 整个农产品分销网络的库存成本Ψ=生产商的库存成本+分销中心的库存成本,p*:分销中心根据公式得到最优的价格: (9) 本节通过算例说明延期支付策略模型前后的利润和库存成本的对比。假设产品农生产商的单位产品成本c=20,单位时间产量为e=4 000,库存费用为k=15,单位售价PM=60。农产品分销中心固定订货费用A=10 000,单位产品订货运输费用s=35,单位产品库存成本h=10,订货周期T=1,分销中心收益IR=8%,农产品生产商支付的利率D=10 000-60PD。 以利息支出和利息收入不同组合的角度,对农产品延期支付期限、农产品生产商利润、农品分销中心利润、农产品分销网络总利润和总库存成本带来的影响进行分析,具体见表1。 表1 利息灵敏度分析 与表1结果对比可以发现所设计的延期支付策略博弈模型显著地提高了农产品生产商利润,降低了分销网络库存。进一步对表1进行分析,分销网络各成员函数值随支付期限变化的趋势如图1所示。 图1 分销网络函数总变化曲线Fig.1 The movement of the distribution network function 从图1可以看出,随着延迟支付期限的增加,分销中心利润有较大增幅,农产品生产商利润有所下降,但分销网络总体利润有所增加;同时分销网络库存成本有所下降。 IP-IR的值对延期支付期限的影响呈现如图2所示。 在最初的假设条件中,假定价格与需求函数为线性函数,对模型结果也有较大影响,,从图2中可以看出延迟支付期限是随着IP-IR的值的减小而不断降低。 农产品生产商支出利息IP和分销中心收入利息IR的变化对于延迟支付期限有着重要的影响,延迟支付期限的支出、收入利息的具体大小与农产品分销网络的具体情况有关。随着延迟支付期限的增加,分销中心利润有较大增幅,农产品生产商利润有所下降,但分销网络总体利润有所增加,同时分销网络库存成本有所下降。 图2 延期支付期限随利率变化曲线Fig.2 The curve of deferred payment period following interest 在表明延迟支付期限选择与订购周期相近时,不仅可以使得生产商利润达到预期的满意度,而且可以使得分销网络总体利润也得到满意的结果。在实际应用中由于参数选择的不同,导致最优延迟支付期限也不同,需要对其进行更深入的博弈分析,但是本文在对延期支付策略和数量折扣策略的研究中仅仅只有2个参与者,因此如何对2级以上的分销网络进行博弈分析需要继续进行探讨。 参考文献: [1]GÜLER M G, BILGI T.On coordinating an assembly system under random yield and random demand[J].European Journal of Operational Research,2009,96(l):342-350. [2]ERLEBAEHER S J,MELLER R D.The interaction of location and inventory in designing distribution systems[J].IIE Transactions, 2000, 32(2): 155-166. [3]DASKIN M S, COULLARD C R. An inventory-location model: formulation, solution, algorithm and computational results[J]. Annals of Operations Research, 2002, 110(l): 83-106. [4]KAZAZ B. Production planning under yield and demand uncertainty with yield-dependent cost and price[J]. Manufacturing and Service Operations Management, 2004, 6(3): 209-224. [5]INDERFURTH K. Analytical solution for a single-period production-inventory problem with uniformly distributed yield and demand[J]. Central European Journal of Operations Research, 2004, 12: 117-127. [6]YANG Shitao, YANG Jian, ABDEL-MALEK L. Sourcing with random yields and stochastic demand: a newsvendor approach[J]. Computers and Operations Research, 2007, 34(12): 3682-3690. [7]KERENA B. The single-period inventory problem: extension to random yield from the perspective of the supply chain[J]. Omega, 2009(37): 801-810. [8]CHANG C T, OUYANG L Y, TENG J T. An EOQ model for deteriorating items under supplier linked to odering quantity[J]. Applied Mathematical Modeling, 2003, 27(12): 983-996. [9]LIAO J J. A note on an EOQ model for deteriorating items under supplier credit linked to ordering quantity[J]. Applied Mathematical Modeling, 2007, 31(8): 1690-1699. [10]朱文贵,朱道立,徐最.延迟支付方式下的存货质押融资服务定价模型[J].系统工程的理论与实践, 2007(12): 1-7. ZHU Wengui, ZHU Daoli, XU Zui. Pricing model for inventory impawn financing under conditions of permissible delay in payments[J]. Systems Engineering-theory and Practice, 2007(12): 1-7. [11]胡劲松,胡玉梅.模糊环境下考虑缺货和延期支付的Stackelberg均衡策略[J].管理工程学报, 2011, 25(2): 87-94. HU Jinsong,HU Yumei. Stackelberg equilibrium strategy with shortage and permissible delay in payments in fuzzy environment[J]. Journal of Industrial Engineering and Engineering Management, 2011, 25(2): 87-94. [12]赵菊,周永务.两层供应链三级库存系统共同生产补货及协调策略[J].系统工程理论与实践, 2012, 32(10): 2163-2172. ZHAO Ju, ZHOU Yongwu. Joint replenishment and channel coordination policy for two echelon supply chain with multi-echelon inventory system[J]. Journal of Industrial Engineering and Engineering Management, 2012, 32(10): 2163-2172. [13]曾文瑛.供应不可靠条件下零售商订货及提前支付策略研究[D].上海: 上海交通大学, 2012: 5-14. ZENG Wenying. Study on retailer’s order and advanced payment strategies under unreliable supply[D]. Shanghai: Shanghai Jiaotong University, 2012: 5 -14.2 农产品生产商为主导的Stackelberg博弈模型



3 算法实例

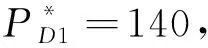


4 结束语
