改进特征样本方法的KPCA变压器故障检测模型
2014-09-12唐勇波
唐勇波
1.宜春学院物理科学与工程技术学院,江西宜春 336000
2.中南大学信息科学与工程学院,长沙 410083
改进特征样本方法的KPCA变压器故障检测模型
唐勇波
1.宜春学院物理科学与工程技术学院,江西宜春 336000
2.中南大学信息科学与工程学院,长沙 410083
针对核主元分析(KPCA)监控模型由于建模样本不纯而导致故障检测失效问题,提出基于改进特征样本方法的KPCA故障检测模型并应用于变压器故障检测中。利用特征值变化信息,设计出异常样本剔除算法以避免异常样本被选入特征样本集;采用特征样本方法提取建模样本集,建立KPCA监控模型,采用复合统计量对变压器运行状态进行检测,实验结果验证了改进特征样本算法的有效性,表明提出的方法具有较高的故障敏感性和检测效率。
电力变压器;故障检测;核主元分析;特征样本
1 引言
油中溶解气体分析(Dissolved Gas Analysis,DGA)是大型油浸式电力变压器内部潜伏性故障检测和诊断的有效手段之一。由于累积效应,采用油中溶解气体的注意值[1-2](即含量限值)来监视变压器运行状况,并不是达到注意值就能确定变压器存在某种故障,而是应该注意跟踪分析。在实际应用中,注意值的设定非常重要,规定得太低也是不经济的,太高是不安全的,通常注意值的设定需要结合安全性和经济性来考虑,具有较大的主观因素,而且,注意值的设定与变压器制造水平有关,制造水平不同,注意值也不相同[3]。
主元分析[4-6](Principal Component Analysis,PCA)为线性降维方法,当用于非线性过程监控时其性能会大大降低[6]。核主元分析(Kernel Principal Component Analysis,KPCA)能有效地提取非线性特征[7-9]。KPCA监控不适合应用于大样本情况,因为计算和存储的核矩阵维数为训练样本的数目。针对这种情况,文献[10-11]提出特征样本(Feature Sample,FS)方法解决了核矩阵的计算问题。但是,文献[10-11]均认为原始样本集中的样本是正常的,不存在异常样本。由于测量手段的局限性、存在测量误差等原因,实际上所采集到的原始样本存在不纯的问题,即含有其他工况数据或潜伏性故障样本,直接采用特征样本方法而不首先剔除这类异常数据,该类数据更容易被选为特征样本,导致监控模型失效。因此,在应用FS算法提取建模样本之前,十分有必要进行建模数据纯化,剔除异常样本。文献[12]提出Fisher判别分析结合可能性C均值聚类的KPCA故障检测算法,但算法较复杂,较难应用。
因此,本文提出改进的特征样本方法,利用特征值变化信息设计出异常样本剔除算法,然后采用特征样本算法提取KPCA建模样本集。变压器DGA实验验证了本文提出的基于改进特征样本方法的KPCA检测模型的有效性。
2 KPCA监控模型
KPCA的基本思想是引入非线性映射φ将输入空间Xn×m映射到高维特征空间F,在高维特征空间中对映射数据φ(xi)的协方差矩阵进行特征向量分析,找到主元。协方差矩阵可以表示为:

CF的特征矢量v可表示为:

其中,ai是相关系数;定义核函数矩阵K=[Kij]n×n,Kij=<φ(xi),φ(xj)>,则公式(2)转化为求解矩阵K的特征值问题:

由K的特征向量a即可求出协方差矩阵CF的特征向量v,即为特征空间的主元方向。通过计算映射数据在特征向量vk上的投影来计算主元,即

其中,<x,y>表示x与y的点积,k为保留主元数,通常采用方差累积百分比(Cumulative Percent of Variance,CPV)来选取。这样,特征空间又可分为主元空间和残差空间。KPCA的求解过程参见文献[7]。
核函数常选用高斯径向基函数:

其中,σ为核宽度。
类似于PCA方法,在主元空间和残差空间中建立KPCA过程统计模型可以实现多变量过程监测。
主元空间中的T2统计量定义为:

虽然T2和SPE统计量在统计过程监控中应用广泛,但有时会出现监测结果不一致,不利于进行故障分析。文献[13]结合T2和SPE统计量,提出一种统一形式的复合统计量。

其中,λc为调整参数,一般可选λc=λk/2;为统计量D的控制限,由核密度估计方法[14]求得。
3 改进特征样本方法的变压器KPCA故障检测模型
3.1 改进特征样本方法
改进的特征样本提取方法(Modified Feature Sample,MFS)分两阶段:第一阶段,对原始正常样本集提纯,剔除可能含有其他工况或含有潜伏性故障等异常样本;其基本思想是利用KPCA模型中最大特征值变化信息来剔除异常样本。简述为:建立n个建模样本的KPCA模型,得到第一个最大特征值λ1(n),并计算n个样本的D统计量,剔除D统计量最大的样本;重新建立n-1个样本的KPCA模型,得到特征值λ1(n-1)和D统计量,判断特征值λ1的变化量Δλ1=|λ1(n)-λ1(n-1)|<λ1(n)/n成立,算法结束;否则,继续剔除D统计量最大的样本。第二阶段,采用特征样本提取方法提取特征样本集。
MFS算法具体步骤如下:
步骤1输入原始正常样本集Xn×m,n为样本数,m为变量数。
步骤2将数据集进行标准化后,按式(6)计算核矩阵K,并按式(10)作均值化处理:

其中,En是元素为1/n的n×n常数方阵。
步骤3按式(4)解决的特征值问题,得到第一最大特征值记为λ1(n)。
步骤4按CPV>85%选取主元数k,并标准化ak,使λ<ak,ak>=1。
步骤5按式(5)提取各样本的非线性主元,并按式(7)和式(8)分别计算各样本的T2和SPE统计量,再按式(9)计算各样本的D统计量。
步骤6剔除D统计量最大的样本,令n=n-1,重复步骤2至步骤5,剔除一个样本后按式(4)解决的特征值问题得到最大特征值记为λ1(n-1)。
步骤7计算特征值的变化量如果Δλ1<λ1(n)/n成立,则结束;否则转至步骤6。
剔除异常样本过程结束后,采用FS算法求取特征样本集,过程如下:
步骤8从数据集任选一个样本到特征样本集S中,令d=1,按式(6)计算相应的核矩阵。
步骤9逐个检验样本,按式(11)计算Δ,设定一个较小的阈值ε>0,如果Δ<ε,则该样本不加入样本集S,否则加入S,令d=d+1,修改相应的核矩阵。

步骤10所有样本检验完毕后,得到特征样本数d和特征样本集S。
3.2 变压器故障检测KPCA建模
DGA是检测变压器早期潜伏性故障的重要手段,DGA检测主要有甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)、氢气(H2)这五种特征气体。变压器运行过程中积累了大量的DGA数据,反映了变压器运行状态的丰富信息,对变压器的故障检测和诊断具有重要价值。传统的注意值判据存在注意值选择和难以解决油中溶解气体浓度的累积效应等问题,难以满足日益增长的变压器故障检测和诊断的需求。KPCA能有效地提取非线性特征,构建统计量能够实现过程监控,在工业过程监控领域应用广泛。因此,本文基于DGA数据,提出变压器故障检测的MFS-KPCA建模,步骤描述如下:
步骤1按3.1节提出的MFS方法剔除原始正常样本集中的异常样本,并获得特征样本集S。
步骤2以特征样本集S作为建模样本集,标准化后按式(6)计算核矩阵K∈Rd×d,并对核矩阵K按式(10)作均值化处理。
步骤3按式(4)解决的特征值问题,按CPV>85%选取主元数k,并标准化ak,使λ<ak,ak>=1。
步骤4按式(5)提取各建模样本的非线性主元,并按式(9)计算各建模样本的D统计量。
步骤5采用核密度估计方法对建模样本D统计量进行估计,取置信度为99%时得到D统计量控制限δ2D。
步骤6输入测试样本集XTE,并标准化。
步骤7对标准化后的每一测试样本xte,计算其内核向量Kte=<xte,xi>,按式(12)均值化处理;xi为建模样本,i=1,2,…,d。

其中,Ed是元素为1/d的d×d常数方阵,Id是元素为1/d的d维行向量。
步骤8按式(5)提取测试样本的非线性主元,并按式(9)计算各测试样本的D统计量。
步骤9将测试样本的D统计量与控制限作比较,如果D≤,正常;否则,故障。
4 实验结果分析
实验选用的变压器DGA样本均为220 kV或500 kV大型油浸式变压器检测样本,其中,原始正常样本(阴性)550例,取自某供电局所辖主变DGA检测样本;故障样本(阳性)275例,部分取自现场,部分来自公开发表的文献。故障检测本质为二分类问题,采用以下指标评价检测性能。
故障敏感性,即阳性样本的分类正确率:

其中,|FN|表示阳性样本分类为阴性的个数,|TP|表示阳性样本分类为阳性的个数。
阴性样本的分类正确率:

其中,|FP|表示阴性样本分类为阳性的个数,|TN|表示阴性样本分类为阴性的个数。
全局的分类正确率:

几何均值Gmean综合考虑了阳性和阴性样本的分类结果。

在这些检测性能评价指标中,最为关注的是故障敏感性和几何均值。
经多次实验,核参数σ=8的性能较好。采用MFS算法对原始正常样本集提取特征样本集,剔除了15个异常样本,表1为MFS算法剔除的异常样本,当ε=10-6时,提取88个特征样本;而采用FS算法,当ε=10-6时,得到84个特征样本,在这84个特征样本中,有13个样本为纯化算法剔除的异常样本,这表明异常样本不先剔除更容易被FS算法选为特征样本。由表1可见,被剔除的样本除14号样本外,至少有一个变量超过注意值。分别采用MFS和FS方法提取的特征样本集建立PCA和KPCA模型,PCA和KPCA模型的分析结果见表2。由表2可见,MFS-PCA的前4个主元的CPV=95.17%,而FS-PCA的前4个主元的CPV=87.55%;MFS-KPCA的前4个主元的CPV=93.78%,而FS-KPCA的前4个主元的CPV=85.33%;并且,取相同的主元数,MFS算法选取的特征样本集建立的PCA或KPCA模型主元捕获数据的变动信息均比FS算法选取的特征样本集建立的PCA或KPCA模型多。可见,MFS算法比FS算法选取的特征样本集更能表征数据特征。

表1 MFS算法剔除的DGA样本(uL·L-1)
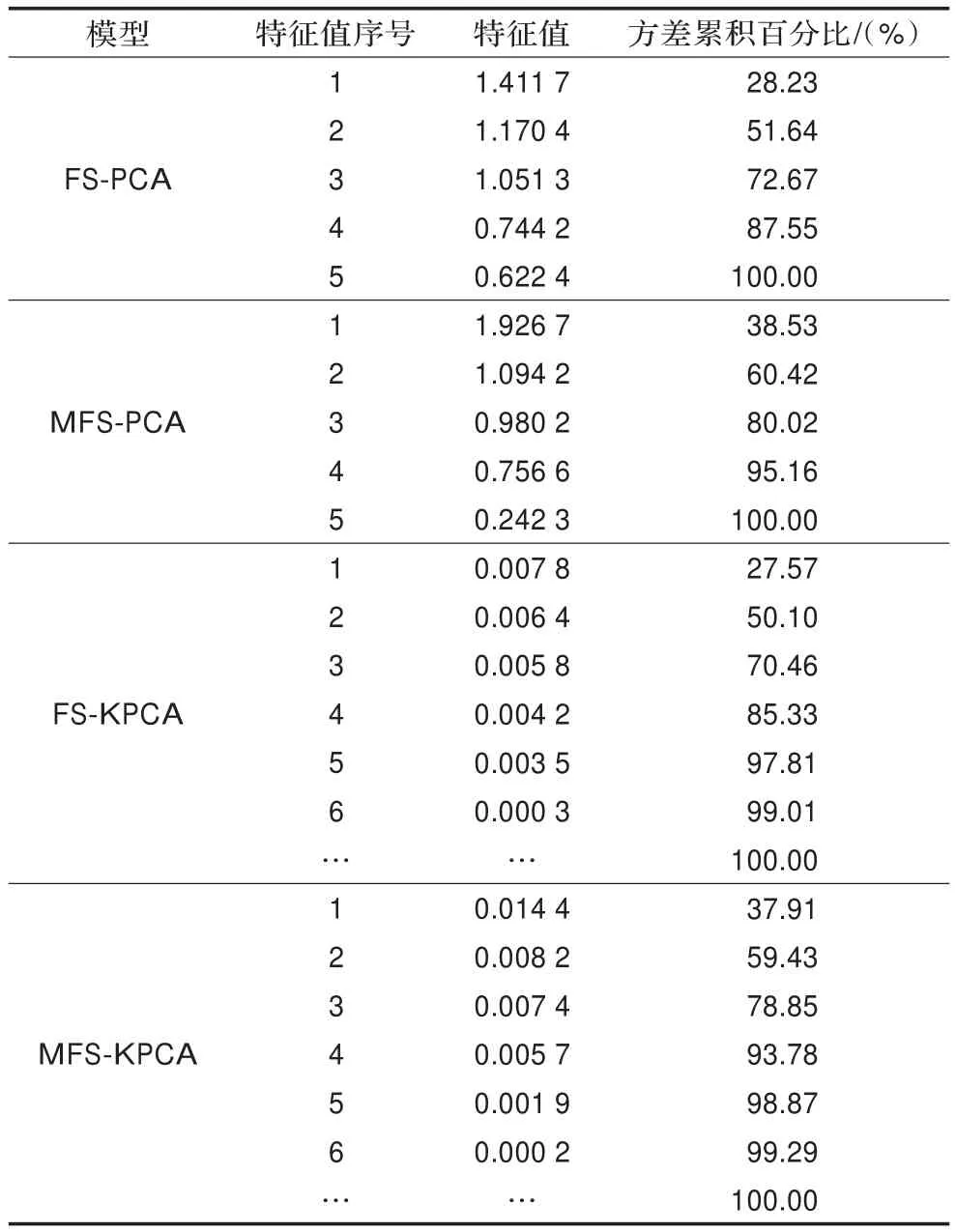
表2 PCA和KPCA模型分析结果
以剔除异常样本剩余的正常样本535例和故障样本275例作为测试样本集,应用于MFS-KPCA,FS-KPCA和MFS-PCA,FS-PCA,其中PCA监控采用文献[15]提出的复合统计量。表3为这几种检测模型的分类性能结果。由表3可见,FS-KPCA虽然tn最高,达到98.69%,但故障敏感性tp却为86.55%,几何均值为92.42%,甚至低于注意值判据,这是由于FS-KPCA的建模样本集中包含较多的异常样本,导致监控模型失效。MFS-KPCA除tn稍低于FS-KPCA和FS-PCA,其他性能指标均为最优,故障敏感性tp达到94.91%,几何均值为96.42%。比较而言,采用MFS提取特征样本集建模的,无论是PCA还是KPCA,均优于FS提取特征样本集建模。充分说明MFS算法能够有效地剔除异常样本,所得到的特征样本集建模优于特征样本方法。

表3 检测结果统计表
另外,阈值ε的选取影响特征样本集的规模,进而影响MFS-KPCA的检测性能,由于KPCA的计算效率取决于建模样本数量,定义KPCA建模效率:

其中,nm为特征样本数,n0为剔除异常样本后的正常样本集的样本数。
显然,特征样本数越小,计算效率越高,另一方面,特征样本数越小,对数据集的特征描述越不充分。图1为阈值ε与γ,tp,Gmean之间的关系图。由图1可见,随ε越小,计算效率γ越低,故障敏感性tp和几何均值Gmean先是逐步增加,在ε=10-6时到达最大值,后降低。综合考虑计算效率和检测效率,阈值ε可选范围在[10-6,10-3]较为适宜。

图1 γ,tp,Gmean与阈值ε的关系曲线
5 结束语
本文针对变压器故障检测中由于建模样本不纯而导致KPCA故障检测模型失效问题,提出了基于改进特征样本的KPCA变压器故障检测模型。利用特征值变化信息提出的改进特征样本方法可以有效剔除异常样本,达到净化建模样本的目的,解决了因异常样本建模导致的检测模型失效问题。MFS-KPCA,FS-KPCA和MFS-PCA,FS-PCA对比实验表明改进特征样本方法的可行性和有效性。MFS-KPCA的故障敏感性和几何均值分别为94.91%和96.42%,高于FS-KPCA的故障敏感性和几何均值分别达8个和4个百分点,验证了MFSKPCA变压器故障检测建模的有效性。
[1]GB/T7252-2001变压器油中溶解气体分析和判断导则[S].北京:国家质量监督检验检疫总局,2001.
[2]廖瑞金,廖玉祥,杨丽君,等.多神经网络与证据理论融合的变压器故障综合诊断方法研究[J].中国电机工程学报,2006,26(3):119-124.
[3]操敦奎.变压器油中气体分析诊断与故障检查[M].北京:中国电力出版社,2005:19-20.
[4]章宗标.一种基于PCA-BP神经网络的示例优选方法[J].计算机工程与应用,2013,49(19):108-111.
[5]唐勇波,桂卫华,彭涛,等.基于重构贡献和灰关联熵的变压器诊断方法[J].仪器仪表学报,2012,33(1):132-138.
[6]Dong D,Mcavoy T J.Nonlinear principal component analysis based on principal curves and neural networks[J]. Computers and Chemical Engineering,1996,20(1):65-78.
[7]Lee J M,Yoo C,Choi S W,et al.Non-linear process monitoring using kernel principal component analysis[J]. Chemical Engineering Science,2004,59(1):223-234.
[8]唐勇波,桂卫华,彭涛.代价敏感核主元分析及其在故障诊断中的应用[J].中南大学学报:自然科学版,2013,44(6):2324-2330.
[9]唐勇波,桂卫华,欧阳伟.基于KPCA和CPSO的故障检测方法[J].计算机工程,2012,38(24):244-246.
[10]付克昌,吴铁军.基于特征子空间的KPCA及其在故障检测与诊断中的应用[J].化工学报,2006,57(11):2664-2669.
[11]Bo Cuimei,Zhang Shi,Zhang Guangming,et al.Fault identification of Tennessee Eastman process based on FS-KPCA[J].Journal of Chemical Industry and Engineering,2008,59(7):1783-1789.
[12]祝志博,宋执环.融合FDA-PCMC样本分类的KPCA故障检测新算法[J].控制与决策,2010,25(4):542-545.
[13]Choi S W,Lee I B.Nonlinear dynamic process monitoring based on dynamic kernel PCA[J].Chemical Engineering Science,2004,59(24):5897-5908.
[14]Chen Q,Wynne R J,Goulding P.The application of principal component analysis and kernel density estimation to enhance process monitoring[J].Control Engineering Practice,2000,8(5):531-543.
[15]Yue H H,Qin S J.Reconstruction-based fault identification using a combined index[J].Industrial and Engineering Chemistry Research,2001,40(20):4403-4414.
TANG Yongbo
1.School of Physical Science and Engineering,Yichun University,Yichun,Jiangxi 336000,China
2.School of Information Science and Engineering,Central South University,Changsha 410083,China
In order to handle the invalidation problem of fault detection when Kernel Principal Component Analysis(KPCA)modeling sample is impure,a new KPCA monitoring model for power transformer fault detection based on Modified Feature Sample(MFS)method is proposed.A new purification algorithm is proposed to eliminate abnormal samples from original database by using eigenvalue variation.Then a Feature Sample(FS)method is adopted to extract modeling samples of KPCA;compound statistics is used to verify the state of power transformer.Experimental results show effectiveness of the modified feature sample algorithm and the proposed method has high fault sensitivity and diagnosis accuracy.
power transformer;fault detection;Kernel Principal Component Analysis(KPCA);feature sample
A
TP277;TM411
10.3778/j.issn.1002-8331.1402-0262
TANG Yongbo.Kernel Principal Component Analysis model for transformer fault detection based on modified feature sample.Computer Engineering and Applications,2014,50(21):4-7.
国家科技支撑计划项目(No.2012BAK09B04)。
唐勇波(1975—),男,博士,副教授,研究领域为智能控制,故障诊断等。E-mail:tybcsu@163.com
2014-02-24
2014-05-04
1002-8331(2014)21-0004-04
CNKI出版日期:2014-05-22,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0262.html
