利用1～2阶分数阶微分掩模的边缘检测

李军成

湖南人文科技学院数学系，湖南娄底 417000

利用1～2阶分数阶微分掩模的边缘检测

李军成

湖南人文科技学院数学系，湖南娄底 417000

现有的分数阶微分边缘检测算子大都是基于0～1阶分数阶微分而构造，鲜有文献讨论基于1～2阶分数阶微分的边缘检测算子。为此，分析了1～2阶分数阶微分对信号的作用，基于1～2阶分数阶微分构造了一种新的边缘检测掩模算子。实验结果表明，该算子不仅优于常用整数阶微分算子，而且比现有的一些0～1阶分数阶微分算子具有更好的边缘检测效果。

边缘检测；分数阶微分；掩模算子；1～2阶微分

边缘检测是图像处理的一个重要环节，也是进行信息提取与模式识别的一个基本手段。传统的边缘检测算子多为微分算子，主要包括一阶与二阶微分算子。常用的一阶微分算子主要有Rebort算子、Sobel算子、Prewitt算子和Canny算子等，而常用的二阶微分算子则有Laplician算子和LOG算子等[1]。

近年来，随着分数阶微积分理论在图像处理领域中的成功应用[2-5]，利用分数阶微分进行边缘检测逐渐成为一个研究热点。Mathieu等人[6]提出了分数阶鲁棒轮廓边缘检测器，适当选择分数阶微分的阶数时，该检测器不仅能选择性地检测出边缘；杨柱中等人[7]构造了一种基于0～1阶分数阶微分的Tiansi掩模模板，相对于传统的微分算子，该模板在有效提取图像边缘的同时具有较高的信噪比；王卫星等人[8]根据Tiansi掩模模板的特点，提出了一种改进的Tiansi算子，该算子在进行边缘检测时可大幅增强图像的纹理细节边缘信息值；Pu等人[9]和Gao等人[10]分别利用分数阶微分替换传统一阶微分，构造了两种不同的分数阶边缘检测算子；汪成亮等人[11]针对Tiansi模板的最佳分数阶阶数需要人为指定这一缺陷，提出了一种基于图像纹理复杂度的自适应分数阶微分算法；何春等人[12]首先利用分数阶微分和分数阶积分组成复合导数，然后在此基础上提出了一种基于复合导数的边缘检测算子；蒋伟等人[13]基于0～1阶分数阶微分理论和传统的Sobel算子，提出了一种分数阶Sobel算子的边缘检测模型。

现有的分数阶微分边缘检测算子大都是基于0～1阶分数阶微分而构造，相对于传统的微分算子，0～1阶分数阶微分算子的边缘检测方法不仅能有效提取图像的边缘信息，而且还能保留图像的纹理细节，对噪声也具有一定的抑制作用。在分数阶微分中，除了可以定义0～1阶分数阶微分，还可定义1～2阶分数阶微分[14]。然而，目前鲜有文献讨论基于1～2阶分数阶微分构造的边缘检测算子。为此，本文基于1～2阶分数阶微分构造了一种用于边缘检测的分数阶微分掩模算子，该算子不仅比常见一阶和二阶微分算子具有更好的边缘检测效果，而且比现有的一些0～1阶分数阶微分算子在边缘信息提取和纹理细节保留方面更具优势。

1 1～2阶分数阶微分

1.1 1～2阶分数阶微分的定义

分数阶微分也称为非整数阶微分，是整数阶微分运算的一种推广。从不同的应用角度分析问题可得到不同的分数阶微分定义。经典的分数阶微分定义主要有Grümwald-Letniko、Riemann-Liouville和Capotu定义[15]。由于Grümwald-Letniko定义是通过将经典微分定义中的阶数由整数扩展到分数推衍而来，在信号的数值实现中表现得更为精确，因此成为图像处理中较为常用的一种分数阶定义。

不失一般性，将函数s(x)的持续期[0，x]进行N等分，共得N+1个节点，这N+1个因果像素点的值分别记为：

将图像的边界作周期扩展，对图像中的非因果像素点进行处理，即

于是，基于Grümwald-Letniko定义可推导出函数s(x)的v阶微分的差分近似公式为[14]：

注：若补充定义Γ(1)=0!=1，则式（1）中的分数阶阶次v满足1≤v≤2，此时将式（1）定义的分数阶微分称为1～2阶分数阶微分。

当k=n≤N-1时，由式（1）可推导出二元函数f(x，y)在x方向和y方向上1～2阶分数阶微分的前3项近似差分表达式可表示为：

不难验证，当v=1时，式（2）与式（3）变为一阶微分的差分近似表达式，即

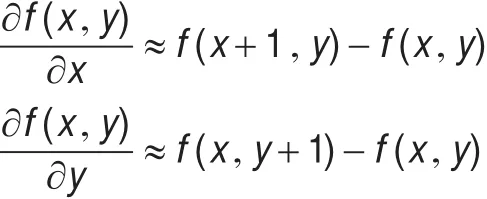
当v=2时，式（2）与式（3）变为二阶微分的差分近似表达式，即

由此可见，1～2阶分数阶微分是一阶与二阶微分的一种推广。

式（4）表明函数f(x，y)在y轴负向和x轴负向上1～2阶分数阶微分的前3项近似差分表达式中的系数之和不为零，这也是1～2阶分数阶微分与整数阶微分的显著区别之一。

1.2 1～2阶分数阶微分对信号的作用分析

将式（1）中的整数阶微分算子Dk推广为任意阶微分算子Dv(v∈R+)，则分数阶微分fv(t)在频域的形式可表示为[7]：

由式（5）与式（6）可得一阶、二阶和1～2阶分数阶微分对信号的幅频特征曲线如图1所示。

图1 微分对信号的幅频特征曲线图

由图1可知，随着微分阶数的增加，微分运算对高频信号的提升作用呈非线性的增长，同时，不同阶数的微分运算对低频信号都有一定的削弱作用。一阶微分运算对甚高频信号的提升作用明显小于二阶微分运算，且对甚低频信号的削弱作用也明显大于二阶微分。虽然1～2阶分数阶微分对甚高频信号的提升作用小于二阶微分，但要大于一阶微分，高频信号得到了足够程度的提升；同时，1～2阶分数阶微分对中低频信号有一定的增强，且对甚低频信号也进行了较大程度的非线性保留。因此，对于纹理细节较为丰富的图像，利用1～2阶分数阶微分进行边缘检测不仅可以较为精确地提取图像的边缘信息，而且还可以较大程度地保留图像的纹理细节。由于边缘和噪声都是高频信号，当图像存在噪声时，1～2阶分数阶微分在增强边缘的同时也会增强噪声，所以由1～2阶分数阶微分对高频信号的提升作用可知，1～2阶分数阶微分的抗噪性比二阶微分好，但要比一阶微分差。在实际应用中，为了获得令人满意的边缘检测效果，可先对图像进行去噪处理后再利用1～2阶分数阶微分进行边缘检测。

图2 不同方向上的掩模算子

2 基于1～2阶分数阶微分掩模算子的边缘检测

2.1 1～2阶分数阶微分掩模算子的构造

与文献[14]类似，依据式（2）与式（3）首先构造出x轴正向和y轴正向上大小为3×3的1～2阶分数阶微分掩模算子，然后类似地可分别构造出x轴负向、y轴负向、左右对角上下方向等6个方向的大小为3×3的1～2阶分数阶微分掩模算子，于是可得8个对称方向上的1～2阶分数阶微分掩模算子，如图2所示。

将所构造的8个方向的掩模算子相加，得到具有旋转同向性的最终1～2阶分数阶掩模算子W(x，y)，如图3所示。

特别地，在W(x，y)中取v=1或v=2且将每一项除以-1，则W(x，y)分别变为：

图3 最终分数阶微分掩模算子

显然，W1(x，y)与W2(x，y)是8-领域的二阶Laplacian算子[1]。由此可见，1～2阶分数阶微分掩模算子是二阶Laplacian算子的一种扩展。

与常用一阶微分算子（如Roberts算子、Prewitt算子、Sobel算子、Canny算子等）以及二阶微分算子（如Laplacian、LoG算子等）相比，本文构造的分数阶微分掩模算子含有1个分数阶参数v，这个参数的取值对图像边缘信息的提取和纹理细节的保留具有重要作用。对于不同的图像，用户也可通过调整分数阶参数v的取值获得不同的边缘检测效果。

另一方面，本文构造的分数阶微分掩模算子是一种基于1～2阶分数阶微分的边缘检测算子，而现有的其他分数阶微分边缘检测模型大都是基于0～1阶分数阶微分而构造，相对而言，本文构造的1～2阶分数阶微分掩模算子在图像边缘的提取和纹理细节的保留方面更有优势。

2.2 算法步骤

设灰度图像函数为f(x，y)，则利用本文构造的分数阶微分掩模算子对图像进行边缘检测的步骤为：

步骤1对图像f(x,y)进行去噪处理，得图像f*(x,y)。

步骤3适当选取分数阶参数v(1＜v＜2)，利用分数阶微分掩模算子W*(x，y)对图像f*(x，y)进行卷积运算，得图像的分数阶掩模运算值G(x，y)=W*(x，y)*f*(x，y)。

步骤4图像的边缘信息值E(x，y)为：

E(x,y)=G(x,y)-f*(x,y)=W*(x,y)*f*(x,y)-f*(x,y)

步骤5适当选取阈值T，得二值化的边缘图像e(x，y)为：

由上述步骤可知，在利用本文算法进行边缘检测时，分数阶参数v和阈值T的大小决定了边缘检测效果。因此，要根据具体的图像合理地选取分数阶参数v和阈值T。在实际应用中，可先对分数阶参数v和阈值T赋予一个适当的数值，若所获得的结果不满意，则可将v和T的取值作适当修改，直到满意为止。

3 实验结果与分析

在PC机上（CPU：Pentium T4400，RAM：2 GB，OS：WIN7 Basic）利用MATLAB7.0软件进行边缘检测实验。实验分为两组。

第1组实验以Lena图为例，对比观察常用一阶、二阶微分算子及本文算法的边缘检测效果，如图4所示。在实验中，Roberts算子、Prewitt算子、Sobel算子、LoG算子及Canny算子的阈值采用Matlab7.0自带的边缘检测函数edge.m中的默认阈值，该阈值是算法根据图像梯度幅值的概率密度而确定；Laplacian算子的最佳阈值取T=70；本文算法中对图像的去噪算法采用的是Matlab7.0自带的3×3自适应Wiener线性滤波函数。

图4 本文算法与常用整数阶微分算子的边缘检测效果对比

由图4可知，Roberts算子检测到的边缘出现了较为严重的不连续现象；Sobel算子和Prewitt算子的边缘检测效果基本相当，都要优于Roberts算子，但纹理细节丢失较多；Laplacian算子在边缘信息的提取方面具有较好的效果，但含有较多的噪声；LoG算子与Canny算子的边缘检测效果较为理想，但由于都利用了高斯函数进行滤波处理，因此也丢失了部分纹理细节；适当选取分数阶参数v与阈值T时，本文算法的两种情况都能较好地提取图像的边缘信息和较大程度地保留图像的纹理细节，且所含噪声较少。另外，由图4也可看出，虽然Canny算子、LoG算子与本文算法都是事先对图像进行去噪处理后再进行边缘检测，但相对而言，本文算子在较好地提取图像边缘信息的同时，图像的纹理信息也得到了较大程度的保留。因此，本文算法的边缘检测效果在总体上要优于常用的一阶与二阶微分算子。

第2组实验以cameraman图为例，对比观察Tiansi算子[7]、分数阶Sobel算子[13]这两种0～1阶分数阶微分算子与本文算法的边缘检测效果，如图5所示。在实验中，文献[7]方法的最佳分数阶参数取v=0.2，阈值取T= 8；文献[13]方法的最佳分数阶参数取v=0.8，阈值取T= 90；本文算法的分数阶参数取v=1.5，阈值取T=80，对图像采用的去噪算法是Matlab7.0自带的3×3自适应Wiener滤波函数。这里，所谓最佳参数指的是使得边缘信息提取、纹理细节保留以及噪声抑制等方面同时取得最好效果时的参数。

图5 不同分数阶微分算子的边缘检测效果对比

由图5可知，与Tiansi算子[7]、分数阶Sobel算子[13]等0～1阶分数阶微分算子相比，本文构造的1～2阶分数阶微分掩模算子在边缘信息提取、纹理细节保留以及噪声抑制等方面都具有优势。因此，本文算法的边缘检测效果在总体上也要优于现有的一些0～1阶分数阶微分算子。

在时间消耗方面，由于本文算法先对图像进行去噪处理，然后再利用3×3掩模模板进行边缘检测，其复杂度要略高于Roberts算子、Prewitt算子、Sobel算子和Laplacian算子，但要低于LoG算子和Canny算子，因此本文算法的时间复杂度是符合实际需要的。

4 结语

本文主要讨论了一种基于1～2阶分数阶微分的边缘检测算子。实验结果表明，当参数适当取定时，该算子不仅比常用一阶和二阶微分算子具有更好的边缘检测效果，而且比现有的一些0～1阶分数阶微分算子在边缘信息提取和纹理细节保留等方面更具优势，为图像的边缘检测提供了一种有效的新方法。由于分数阶微分掩模算子的分数阶参数和阈值需要人为设定，对于实时性要求较高的场合不太适用，因此如何根据图像的特点自适应选取阈值及分数阶参数值将是进一步的研究问题。

[1]许录平.数字图像处理[M].北京：科学出版社，2007.

[2]Liu J，Chen S C，Tan X Y.Fractional order singular value decomposition representation for face recognition[J].Pattern Recognition，2007，41（1）：168-182.

[3]杨柱中，周激流，晏祥玉，等.基于分数阶微分的图像增强[J].计算机辅助设计与图形学学报，2008，20（3）：343-348.

[4]Pu Y F，Zhou J L，Yuan X.Fractional differential mask：a fractional differential-based approach for multiscale texture enhancement[J].IEEE Trans on Image Processing，2010，19（2）：491-511.

[5]Zhang J，Wei Z H.A class of fractional-order multi-scale variational models and alternating projection algorithm for image denoising[J].Applied Mathematical Modeling，2011，35（5）：2516-2528.

[6]Mathieu B，Melchior P，Outsaloup A，et al.Fractional differentiation for edge detection[J].Signal Processing，2003，83（11）：2421-2432.

[7]杨柱中，周激流，黄梅，等.基于分数阶微分的边缘检测[J].四川大学学报：工程科学版，2008，40（1）：152-157.

[8]王卫星，于鑫，赖均.一种改进的分数阶微分掩模算子[J].模式识别与人工智能，2010，23（2）：171-177.

[9]Pu Y F，Zhou J L.A novel approach for multi-scale texture segmentation based on fractional differential[J].International Journal of Computer Mathematics，2011，88（1）：58-78.

[10]Gao C B，Zhou J L，Hu J R，et al.Edge detection of color image based on quaternion fractional differential[J]. IET Image Processing，2011，5（3）：261-272.

[11]汪成亮，乔鹤松，陈娟娟.基于纹理复杂度的自适应分数阶微分算法[J].计算机工程，2012，38（7）：177-178.

[12]何春，叶永强，姜斌，等.一种基于分数阶次微积分模板的新型边缘检测方法[J].自动化学报，2012，38（5）：776-787.

[13]蒋伟，陈辉.基于分数阶微分和Sobel算子的边缘检测新模型[J].计算机工程与应用，2012，48（4）：182-185.

[14]张意，蒲亦非，周激流.分数阶微分掩模及其滤波器的构造[J].华南理工大学学报：自然科学版，2011，39（7）：95-101.

[15]Podlubny I.Fractional differential equations[M]//Mathematics in Science and Engineering.[S.l.]：Academic Press，1999，198：150-158.

LI Juncheng

Department of Mathematics,Hunan University of Humanities,Science and Technology,Loudi,Hunan 417000,China

The present fractional differential operators for edge detection are constructed based on 0～1-order fractional differential.There are rare papers which discuss the edge detection based on 1～2-order fractional differential.This paper analyses the effect of 1～2-order fractional differential to signal,and then constructs a novel mask operator for edge detection based on 1～2-order fractional differential.Experimental results demonstrate that the novel fractional operator is better than the normal integer order differential operators,and has better edge detection results than some present 0～1-order fractional differential operators.

edge detection;fractional differentiation;mask operator;1～2-order differential

A

TP391

10.3778/j.issn.1002-8331.1403-0184

LI Juncheng.Edge detection using 1～2-order fractional differential mask.Computer Engineering and Applications, 2014,50（21）：14-18.

湖南省自然科学基金（No.13JJ6081）；湖南人文科技学院省级重点建设学科“计算机应用技术”资助。

李军成（1982—），男，博士在读，主要从事计算机辅助几何设计、数字图像处理等方面的研究。

2014-03-14

2014-04-29

1002-8331（2014）21-0014-05

CNKI出版日期：2014-05-22，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1403-0184.html