模型导向的矩形建筑物三维重建
2014-09-12杨玲阮心玲
杨玲,阮心玲
河南大学环境与规划学院,河南开封 475004
模型导向的矩形建筑物三维重建
杨玲,阮心玲
河南大学环境与规划学院,河南开封 475004
针对以航空影像为数据源的矩形建筑物半自动重建进行了研究。采用模型导向的方法,用CSG与B-Rep相结合描述的矩形体基本模型,提取航空影像中建筑物边缘线,人机交互建立建筑物的初始模型;将初始模型反投到影像上,根据建筑物边缘与模型投影线之间套合程度,通过基于广义点摄影测量理论的模型影像匹配算法计算建筑物的精确参数。该方法利用影像上的直线信息进行广义点平差,减少运算量,提高建模效率与建模精度。实验结果证明该方法有较高的准确性。
建筑物三维重建;广义点;矩形建筑物模型;模型影像匹配
1 引言
目前,智慧城市的发展对自动或半自动建立城市三维模型的需求越来越多。由于航空影像获取的便捷性、高效性和高信息容纳性,用摄影测量的方法以大比例尺的航空影像为数据源获取建筑物的三维几何信息和表面的纹理,是实现三维建筑物重建的有效途径之一[1]。从航空影像自动提取建筑物的研究成果已经有很多,但是由于建筑物的复杂性,至今仍然没有一种能够对所有建筑物进行全自动重建的方法,全自动化以及如果减少人工干预依然是建筑物三维重建中的难题[2-4]。
模型导向的建筑物三维重建方法一般流程为:(1)构建模型元件(primitive)库,并根据布尔运算将复杂建筑物分割为一系列元件;(2)根据成像将元件投影到影像上,并对影像上建筑物进行边缘提取;(3)迭代计算模型参数使得模型在影像上的投影线与影像上建筑物边缘配准。这类方法能取得较好的效果,但也存在一定问题,主要表现在模型与影像匹配计算时所采用的匹配模型较为复杂,常用的模型有:最小二乘模型影像套合法[5-7]、直线摄影测量法[8]与遗传算法[9]。最小二乘模型影像套合法以影像上提取建筑物边缘点到模型投影线距离为观测值,直线摄影测量法以模型线端点投影到其在影像上共轭直线的距离为观测值,两者观测方程都比较复杂不易线性化,而遗传算法运算时间过长、不易于掌控。
本文针对比较常见的矩形建筑物,根据模型导向的方法,首先利用影像上提取的直线信息计算矩形建筑物的初始模型参数,而后根据最邻近直线广义点平差算法迭代计算建筑物模型的精确参数,以提高自动化程度,简化观测方程,减少计算量,提高计算效率。
2 模型元件的描述与参数
模型元件是组成建筑物的最小单元,其附带一组参数,可根据参数调整模型形状、空间位置与姿态。模型参数包括形状参数和姿态参数。形状参数用以描述模型的尺寸或外形;姿态参数用于描述模型的位置与方位。三维模型的描述方法很多,CSG模型[6]与B-Rep[6]是较为常用的方法,本文采用二者结合的方式来描述矩形基本模型,即以CSG模型描述形状与姿态参数,B-Rep定义模型内的点线面关系。
2.1 矩形基本模型
矩形模型元件是一个边长为1的立方体,角点编号如图1所示,编号为0的角点为模型坐标系统的原点,定义为基点。

图1 矩形建筑物基本模型
矩形模型的形状参数有3个:长(L1)、宽(L2)、高(H),分别决定矩形模型在Xm、Ym、Zm方向上的尺寸,无论形状参数如何变化,矩形体的形状保持不变,由B-Rep定义的点线面关系也保持不变。姿态参数为基点坐标(dX,dY,dZ)以及绕X轴的旋转角s、绕Y轴的旋转角t以及绕Z轴的旋转角a。故矩形模型可以用9个参数(L1,L2,H,dx,dy,dz,s,t,a)描述。根据立方体特征很容易获取矩形建筑物各个角点在模型坐标系下的坐标[4]。
2.2 坐标系统转换
由于实体模型是定义在模型空间坐标系,而三维模型定义在大地坐标系统下,且模型需要投影到影像坐标系下,影像坐标系与屏幕坐标系也不相同,所以模型实体要经历一系列的坐标变换,如图2所示。

图2 坐标系统转换
为方便计算,本文采取先缩放再旋转后平移的顺序将建筑物初始模型由模型空间坐标系转换到物空间坐标系,旋转时采用摄影测量中以y轴为主轴的方式,旋转矩阵(RR)可以表示为:

其中m1i,m2i,m3i含义与摄影测量[10]中ai,bi,ci一致,本文不再详述。
若某点P在模型坐标系中的坐标为(X0,Y0,Z0),其在物空间坐标系下的坐标为(X,Y,Z),则(X,Y,Z)是(dx,dy,dz,L1,L2,H,s,t,a)的函数,表达式为:

若影像内外方位元素已知,可以根据共线方程[10]将空间坐标系中的建筑物角点坐标逐个投影到影像上,按照角点编号以及预先定义的B-Rep点线面关系即可重组模型边缘。
3 初始模型参数计算
本文通过建筑物边缘直线来计算模型参数的初始值。如图3所示,模型基准线为通过模型基点且能计算模型参数的边线。
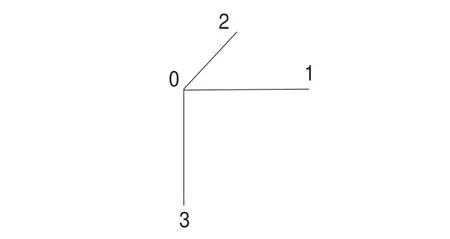
图3 矩形建筑物模型基准线
若已知基准线及其端点坐标,则模型参数的初始值可以通过公式(2)计算。

其中,(X0,Y0,Z0)为基点(点0)的坐标,dis表示两点间的距离,pt0,pt1,pt2,pt3分别为图3所示的点0、1、2、3。
已知四个点在模型坐标系与物空间坐标系中的坐标,很容易求得两个坐标系间的旋转矩阵RR,具体方法此处不再详述。而(s,t,a)可以通过以下公式计算:

其中,mij为RR矩阵中的元素。
为得到影像中建筑物边缘直线信息,必须对影像进行边缘提取,本文采用log算子提取建筑物边缘,然后通过直线跟踪、拟合、最小二乘直线模板匹配、断裂共线直线段的自动识别与合并等操作得到建筑物的边缘直线段。在多像的情况下,物方点与像点满足摄影测量中的空间前方交会,见公式(4),给定一组(x,y),通过公式(5)可计算其物空间坐标,按公式(2)、(3)即可求得模型参数的初始值。

模型初始参数有一定的不准确性,所以初始模型反投影到影像上模型边缘线并不能与影像中建筑物边缘很好地吻合,所以需要用迭代算法计算最佳模型参数。
4 广义点平差迭代计算模型参数精确值
本文使用广义点平差理论代替传统的根据点线距离的最小二乘平差方法,由最佳对应边缘线广义点平差迭代的算法求取模型参数的精确值。张祖勋提出的广义点摄影测量理论是对基于点的摄影测量理论的扩展,它将点、直线、圆、圆弧、任意曲线以及灭点归纳为一个数学模型进行统一平差[11-15]。广义点平差的基本数学形式与摄影测量中传统的共线方程类似,如公式(6)所示。式中,θ是影像特征在(x,y)处的切线角度,物方直线投影到影像上,根据θ的不同仅取它与对应直线上沿x或y方向的残差;(X,Y,Z)为(dx,dy,dz,L1,L2,H,s,t,a)的函数。
广义点误差方程中的直线采用有6个未知数的两点式来表达,而空间直线的自由度是4,直线上任意两点都可表达直线,平差迭代很难收敛,因此必须增加两个独立的限制条件。
由于节点是建筑物模型的基本数据,模型中的线均为节点的连线。本文采取基于模型的重建方法,建筑物中任意节点都可以表示为9个模型参数的函数,因此,可以直接用模型参数表示模型的3D直线边缘进行平差计算,其原理类似于带有限制条件的间接观测平差模型。
在进行广义点平差理论迭代计算前,需根据一定的规则搜索确定模型边缘线在影像上对应的直线。搜索时只需考虑可见的边缘投影线,根据初始投影线设定一定的搜索区域,计算搜索区域内直线与投影线的相似性,选择最佳对应直线。

根据上式即可建立方程,迭代计算得到模型参数最佳值。
5 实验与分析
本文选择两组航空摄影数据分别进行实验,每组数据均使用两张已知内外方位元素的影像。实验流程如下:首先根据人的先验知识建立建筑物模型、建筑物坐标系并设定模型参数;然后提取建筑物边缘直线,人工在影像上选择任意一对位于建筑物顶部没有被遮挡的共轭角点作为基点,搜索基准线,并计算模型参数的初始值,建立初始模型;再将初始模型反投到影像上,搜索最佳对应边缘线,最后进行广义点平差迭代计算模型参数的精确值。
从第一组数据的实验结果看,最小二乘平差迭代算法中,第一张影像中提取的边缘像素点为206 533个,抽稀后边缘点数为8 326个,第二张影像中边缘点数为235 496个,抽稀后点数边缘特征点数量为9 502个,取投影边缘线左右5个像素为计算区域,则两张影像建立的观测方程数目为1 993个。
第二组数据实验结果显示:最小二乘平差迭代算法中,第一张影像中提取的边缘像素点为122 894个,抽稀后边缘点数为5 679个,第二张影像中边缘点数为120 963个,抽稀后点数边缘特征点数量为5 873个,同样取投影边缘线左右5个像素为计算区域,则两张影像建立的观测方程数目为1 637个。
基于广义点平差的迭代计算中,由于矩形建筑物共有12条边,两组数据中每张影像上的可见边数均为9,所有可见的投影边缘线均可以在影像上搜索到对应边缘线,所有9条边都有对应的影像边缘线,则广义点平差的观测方程个数为36个。
若建筑物的参数初始值相同(均通过建筑物模型的基线信息计算得到),设置迭代次数均为20次,实验在同一台计算机上进行。结果显示:最小二乘模型影像配准算法,第一组数据耗时6 s,第二组数据耗时4 s,而基于广义点的迭代算法两组数据耗时均不到1 s。
计算所得参数在影像上的投影如图4和图5所示,由于没有进行实地量测,以上建筑物的坐标与形状参数未知,所以未能进行精度计算。但是从图4和图5可以看出,第一组初始值的误差最大为5个像素左右,最小二乘法迭代后结果改善不明显,基于广义点摄影测量的模型与影像配准结果较好,模型投影边缘线都与影像上提取的特征直线良好。第二组数据的初始值误差最大约为10个像素,最小二乘法迭代后结果有所改善,基于广义点摄影测量的模型与影像配准结果与影像中建筑物边缘更为接近。平差的模型影像配准计算量较小,耗费时间短,计算结果精度较高,模型与影像的配准能达到全自动化。

图5 第二组数据实验结果

图4 第一组数据实验结果
仍然存在不完全吻合的情况,其原因如下:(1)精确参数计算主要依赖于影像上能提供的边缘信息,影像分辨率高,计算结果会较为理想,反之,计算结果依然存在误差。(2)航空影像中建筑物的底部大部分被遮挡,纹理不清晰。(3)特征提取的算法与参数选择,不同的算法和参数提取的边缘数据不完全相同,计算结果自然也存在差别。
为评价本文算法的精确性,选择一个尺寸已知的长方体积木模拟矩形建筑,放置在一个圆形平台上,以平台中心为原点,绕平台一周,每旋转15°拍摄一次,共获取24张影像,将影像分为12组,每组2张。以平台平面为XOY平面,Z轴竖直向上,建立物方坐标系。采用本文方法对12组数据分别实验,流程与前文两组数据一致,并统计12组结果的均值与方差,具体结果如表1所示。由于现实中建筑物大多数垂直于地表,即物方坐标系与模型坐标系的Z轴平行,这种情况下,模型的旋转参数t=s=0。在模拟实验中,也采取积木底部平行于地面,t、s不参入计算,旋转参数只有a。计算结果如表1所示,表中长度单位为毫米(mm),角度单位为弧度(rad)。

表1 长方体积木计算结果比较
因此,与最小二乘模型影像配准相比,基于广义点
从表1中可以看出,广义点摄影测量法所得计算结果所有未知数的均值都更加接近真实值,而且方差也比最小二乘法小,可见本文方法精度高于传统的最小二乘法计算结果。从计算时间来看,此实验中,广义点摄影测量法计算时间不到1 s,最小二乘法耗时为3 s左右。
6 结束语
实验证明本文的算法能较有效地对建筑物半自动三维重建,避免了传统方法中点匹配与直线跟踪与拟合等复杂的计算,大幅度减少计算时间,并且能达到较高的精度。本文中算法不需要其他辅助数据,人工操作部分只涉及1对基点的选择与模型选择,充分利用了人脑的先验识别能力与计算机的数字计算能力,提高了效率和应用范围。
[1]江万寿.航空影像多视匹配与规则建筑物自动提取方法研究[D].武汉:武汉大学,2004.
[2]张剑清,张祖勋,徐芳,等.城区大比例尺影像三维景观重建[J].武汉测绘科技大学学报,1998,23(4):355-358.
[3]程曦冉,张剑清,张祖勋.航空影像多直角平顶房屋的半自动提取[J].武汉大学学报:信息科学版,2004,29(12):1097-1100.
[4]杨玲,张剑清.基于模型的航空影像矩形建筑物半自动建模[J].计算机工程与应用,2008,44(33):10-12.
[5]Veldhuis H.Performance analysis of two fitting algorithms for the measurement of parameterised objects[J].International Archives of Photogrammetry and Remote Sensing,1998,32:400-407.
[6]Lowe D G.Fitting parameterized three-dimensional models to images[[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1991,13(5):441-450.
[7]Vosselman G.Interactive alignment of parameterised object models to images[J].International Archives of Photogrammetry and Remote Sensing,1998,32:272-278.
[8]Van den Heuvel,Frank A.A line-photogrammetric mathematical model for the reconstruction of polyhedral objects[C]// Proceedings of SPIE,San Jose,CA,USA,1999.
[9]林志交.基因演算法于模型影像套合计算之应用[D].中国台湾:国立成功大学,2002.
[10]王之卓.摄影测量原理[M].北京:测绘出版社,1980.
[11]张祖勋,张剑清.广义点摄影测量及其应用[J].武汉大学学报:信息科学版,2005,30(1):1-5.
[12]唐敏,张剑清,张祖勋.基于广义点理论的多基线影像钣金件3D重建与尺寸检测[J].武汉大学学报:信息科学版,2007,32(12):1095-1098.
[13]杨玲.基于广义点摄影测量理论的模型导向建筑物三维建模研究[D].武汉:武汉大学,2009.
[14]郑顺义,郭宝云,李彩林.基于模型和广义点摄影测量的圆柱体自动三维重建与检测[J].测绘学报,2011,40(4).
[15]李畅,李芳芳,李奇,等.一种利用广义点和物方补偿纠正建筑影像的算法[J].武汉大学学报:信息科学版,2012,37(10):1232-1235.
YANG Ling,RUAN Xinling
College of Environment and Planning,Henan University,Kaifeng,Henan 475004,China
A semi-automatic 3D building modeling method based on aerial images is proposed.Building model is built, building edges are extracted from the aerial images,and the accurate model parameters(position parameters and shape parameters)of buildings are calculated based on generalized point photogrammetry theory.The primitive model of buildings is described by CSG and B-Rep.The initial parameters of model are calculated through human-computer interaction.The initial model is projected to images according to the collinearity equation,and the exact parameters are calculated based on generalized point photogrammetry theory.Experiments are done to prove validity of the algorithm.
buildings 3D reconstruction;generalized point;cube building model;model-image fitting
A
TP39
10.3778/j.issn.1002-8331.1312-0230
YANG Ling,RUAN Xinling.Model-driven method of cube buildings 3D reconstruction.Computer Engineering and Applications,2014,50(21):24-28.
国家自然科学基金(No.41101450,No.41201402)。
杨玲(1983—),女,博士,副教授,研究领域为数字摄影测量、计算机视觉、数字图像处理;阮心玲(1977—),男,博士,副教授,研究领域为地理信息系统、统计分析。E-mail:yangling0606@163.com
2013-12-17
2014-05-16
1002-8331(2014)21-0024-05
CNKI出版日期:2014-06-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1312-0230.html
