液化天然气及天然气物性计算软件设计①

田士章 陈 帅 杨 波

(1.中石油大连液化天然气有限公司 2.中海广东天然气有限责任公司)

LNG接收站主要用于接收、储存和气化LNG，并通过外输天然气管道向用户提供天然气。LNG接收站工艺流程简图如图1所示。LNG由卸料臂输送至储罐存储，然后通过储罐中的低压泵加压至槽车和高压泵；至槽车的LNG直接由槽车至用户，而高压泵则将LNG再次加压，输送至气化器将LNG气化为NG，NG通过计量系统输送至外输管网。接收站在正常运行过程中，由于LNG储罐自身漏热、LNG管线保冷漏热等因素[1-2]会有BOG产生，这些BOG经过压缩机加压后，再由再冷凝器冷凝[3-4]为LNG输送至高压泵。而在接收站的整个运营过程中，液化天然气和天然气物性是其安全、高效、节能运行的基础。因此，为了给接收站的生产、运行提供帮助，设计了一款适用于液化天然气及天然气物性计算的软件。

1 BWRS方程

1.1 状态方程选择

目前，计算天然气混合物的状态方程有很多，常用的有LKP、P-R、RK、RKS、BWR等状态方程[5-8]。而Starling和Han在关联大量实验数据基础上提出的修正的BWR状态方程(简称BWRS方程)，对扩大原BWR方程的应用范围及进一步提高其精度取得了良好的效果。同时，此方程被认为是当前烃类计算中最佳模型之一。因此，选择BWRS方程作为整个软件设计的理论基础。

1.2 BWRS方程中各参数求法

BWRS方程形式如下：

(1)

式中，p为介质绝对压力，kPa；ρ为介质密度，kg/m3；R为气体常数，kJ/(kmol·K)；T为介质温度，K。

式(1)中的各参数A0、B0、C0、D0、E0、a、b、c、d、α、γ可通过文献[9]中的方法来求解；不同组分混合的二元交互系数则可通过查阅文献[10]中的表2获得；计算中所需的天然气各纯组分临界参数可通过表1查询而得。

表1 天然气各纯组分临界参数

2 物性参数求解

2.1 密度及气体压缩因子求解

在给定介质组分后，通过方法(1)求解出BWRS方程的11个参数。将BWRS方程变形为以下函数形式：

(2)

在给定了温度T和压力p后，求解方程(2)便可求得介质密度ρ。由于此方程为高阶非线性方程，直接求解难度非常大，所以采用正割法[9]进行求解。正割法对应迭代公式如下：

(3)

式中，k为迭代序号。而在用正割法求解时需要给定两个初值ρ0、ρ1(求解NG密度：ρ0=0，ρ1=p/RT；求解LNG密度：ρ0=40 kg/m3，ρ1=3 840 kg/m3)。同时，|ρk+1-ρk|≤ερ(其中，ερ=10-6)迭代收敛，ρk+1即为所求密度。

2.2 定压及定容比热计算

2.2.1纯组分理想气体定压比热容求解

纯组分理想气体定压比热容可按式(4)线性回归式[11]求解。

(4)

2.2.2LNG定压比热容求解

求解LNG定压比热容时，首先采用Sternling-Brown方程[12]求解出纯物质液体定压比热容，然后按照理想气体混合规则求解出LNG定压比热容cp_LNG(kJ/(kmol·K)。

Sternling-Brown方程：

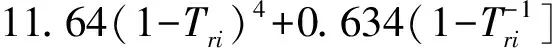
(5)

式中，cpLi为纯组分i的液体定压比热容，kJ/(kmol·K)；ωi为纯组分i的偏心因子；Tri为纯组分i的对比温度(Tri=T/Tci)。

2.2.3天然气定容比热容及定压比热容求解

(6)

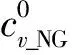
在求解出天然气理想气体定容比热容后，根据式(7)方可求得天然气定容比热容；再由式(8)得到天然气定压比热容。

(7)

式中，cv_NG为天然气定容比热容，kJ/(kmol·K)。

(8)

式中，cp_NG为天然气定压比热容，kJ/(kmol·K)。而其中的偏微分式可通过以下方程式求得：

(9)

(10)

2.3 焓、熵计算

2.3.1理想气体焓、熵求解

纯组分理想气体焓、熵可按照式(11)、(12)线性回归式[11]求解。

(11)

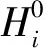
(12)

2.3.2LNG或天然气焓、熵求解

在求解出天然气理想气体焓、熵后，可根据式(13)、(14)的余焓、余熵式求解出LNG或天然气的焓、熵值。在求解LNG焓、熵时，式(13)、(14)中的密度ρ为2.1节中的LNG液体密度；求天然气焓、熵时则为2.1节中天然气密度。

(13)

(14)

式中，Hm为LNG或天然气焓，kJ/kmol；Sm为LNG或天然气熵，kJ/(kmol·K)；ρ0=101.325/RT，kg/m3。

2.4 天然气绝热节流降压后温度计算

由于天然气绝热节流过程[13-15]可以近似地看作等焓过程，所以其节流前和节流后的焓值是相等的。而节流前压力、温度和节流后的压力通常是已设定的。因此，可以通过2.3节直接求出节流前的焓值，对于节流后的温度则可用正割迭代法来求解。具体求解方法为：

首先,由Hms=f(Ts,ps)求解出节流前天然气焓值。Hms为节流前焓值，kJ/kmol；Ts为节流前天然气温度，K；ps为节流前天然气压力，kPa。然后以节流后温度为变量，建立节流前后焓差函数，如式(15)所示。

F(Te)=Hme(Te,pe)-Hms=0

(15)

式中，Te为节流后温度，K；pe为节流后压力，kPa；Hme为节流后由Te、pe根据2.3节计算得到的焓值，kJ/kmol。

建立如下正割迭代式：

(16)

式中，k为迭代序号。而在用正割法求解时需要给定两个初值Te0、Te1(Te0=Ts-(ps-pe)×0.005，Te1=Ts-(ps-pe)×0.003)；同时，当|Tek+1-Tek|≤εTe(其中，εTe=10-2)迭代收敛时，Tek+1即为所求温度。

2.5 天然气发热量计算

软件主要针对LNG接收站所设计。考虑到接收站发热量参比温度范围，所以软件设计的天然气燃烧发热量参比温度范围为(0～20 ℃)，而参比压力则为101.325 kPa。

2.5.1摩尔发热量计算

理想气体纯组分在燃烧参比温度为20 ℃、15 ℃和0 ℃时的摩尔发热量可查阅文献[16]获得。根据文献[16]给出的数据，通过式(17)方可求得天然气理想气体对应温度的摩尔发热量。由LNG气化得到的天然气，其理想气体摩尔发热量与真实气体摩尔发热量误差不会超过50 J/mol,所以软件将以理想气体摩尔发热量近似为天然气真实气体的摩尔发热量[16-17]。而对于0 ～20 ℃范围内非表6中的温度点对应的摩尔发热量，则根据线性插值法求解。

(17)

2.5.2体积发热量计算

通过式(7)求解出天然气理想气体摩尔发热量后，可根据式(18)得出天然气理想气体体积发热量。再由2.1节中的方法求解天然气在计量参比温度、压力下的压缩因子，最后通过式(19)便能得到天然气体积发热量。

(18)

(19)

2.6 特殊组分泡点计算

接收站的LNG泡点计算主要应用在低压区。同时，LNG组分通常比较固定。所以软件设计了4种特殊组分(见表2)压力范围在50～4 000 kPa的泡点计算。首先由Apsen_Plus[18]计算出4种组分在压力范围内的对应泡点温度；然后由MATLAB软件[19]拟合出“压力-泡点温度”和“温度-泡点压力”的函数关系式；最后在软件中设计出4种组分泡点压力和温度的计算。实际应用中，对于非4种组分的实际LNG，则可以选择与其最接近的组分形式作为近似计算值。

表2 LNG中4种特殊组分

拟合公式如式(20)所示，并在表3中给出了对应的拟合参数。

(20)

式中，pbp为泡点压力，kPa；Tbp为泡点温度，K；qi为拟合式参数。

表3 泡点压力、温度回归式参数

qi式20-E式20-F式20-G式20-H183.970 488 961 062 6-350.366 930 577 69-211.172 931 819 20130.483 213 964 837 420.000 602 382 328 488 385529.114 599 323 563365.582 335 602 66656.658 826 345 375 735.618 239 163 374 57×10-10-274.544 403 373 088-192.386 001 722 561-23.314 961 262 073 741.125 274 446 857 6479.333 973 429 146 156.686 893 975 107 95.253 367 351 894 7650.348 858 266 821 844-13.577 608 120 783 3-9.881 678 271 508 56-0.419 689 207 049 15861.381 109 536 744 011.024 433 596 293 97-0.044 353 660 368 776 57-0.077 204 368 369 392-0.058 382 677 367 2860.012 971 973 686 439 880.001 832 482 988 387 10.001 414 571 302 456 7-0.001 088 508 724 977 9390.000 033 059 870 227 543 6

3 软件使用说明

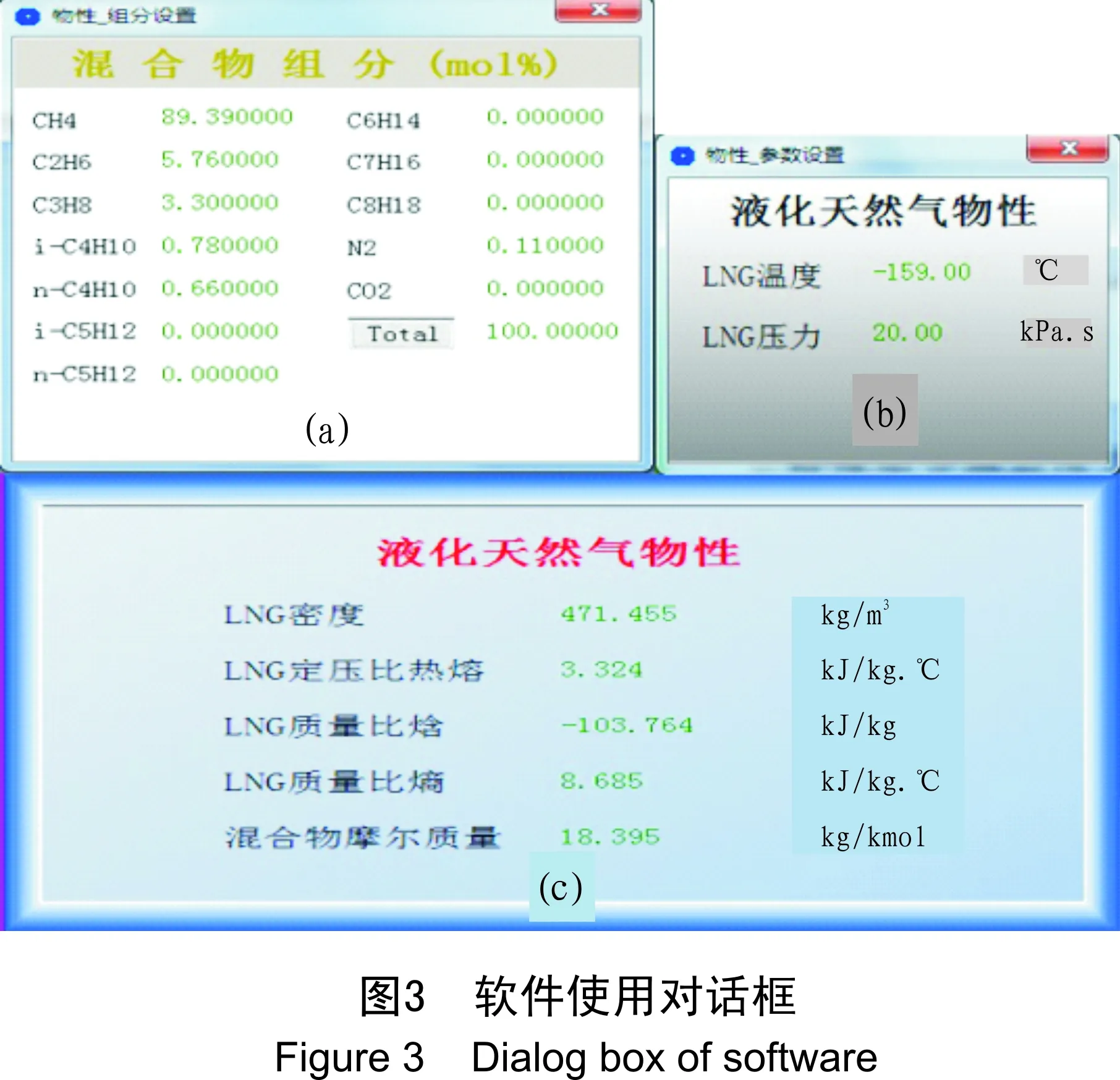
根据以上所做的研究和分析，在Forcecontrol V7.0平台上设计出LNG及天然气相关物性的计算软件[20]，图2为软件人机界面。在使用过程中，首先点击“设置”按钮，通过弹出的“物性_组分设置”对话框(图3a)输入各组分的摩尔分数；然后点击计算选择项按钮，通过弹出的“物性_参数设置”对话框(图3b)输入计算所需的基本参数值；最后，点击“运算”按钮执行计算，结果则会在计算结果显示窗口中显示(图3c)。

4 软件计算结果误差分析

软件计算物性参数较多，所以在此选择LNG接收站常用的密度、焓和高位发热量作误差分析。

4.1 密度及高位发热量误差分析

对比大连接收站实际工况运行中3种LNG(天然气)组分所对应的实测LNG密度，天然气密度、高位发热量和软件计算相同工况的值，求出相对误差。表4为实际运行组分，表5为对应工况误差分析数据列表。

表4 大连接收站实际运行组分 (y/%)

通过表5的相对误差可以看出：①计算LNG密度时，最大相对误差为1.177 8%；②计算天然气密度时，最大相对误差为-0.133 8%；③由于天然气高位发热量是经GB/T 11062-1998《天然气发热量、密度、相对密度和沃泊指数的计算方法》中的数据处理而来，所以其相对误差非常小，最大只有0.007 7%。同时，为了检测BWRS方程为最佳选择方程，也采用了其他状态方程对以上3种工况进行了计算。在计算LNG密度时， LKP方程最大相对误差为2.731 6%、P-R方程为-1.625 4%、RKS方程为2.283 9%；计算天然气密度时，LKP为2.567 6%、P-R为1.895 7%、RKS为-2.332 4%。由此可以看出，在密度计算上BWRS方程精度最高；虽然其形式比较复杂，在计算上相对困难，但经过软件设计后已很好地克服了此问题。

表5 密度及高位发热量误差分析数据

4.2 焓误差分析

焓作为LNG接收站运行能耗分析的重要物性参数，通常无法直接获取。因此，将Apsen_Plus软件计算的相应工况焓差与此软件计算的对应工况焓差进行对比，以计算其相对误差。表6给出了2.6节中常规气的相关焓误差分析数据。

表6 焓误差分析数据

通过表6焓差的最大相对误差可以看出，软件所计算的最大相对误差为0.884 4%，远远小于工程上所要求的5%，所以软件可很好地计算LNG和NG的焓值。由于通常采用状态方程计算物性中密度是其他参数计算的基础，而在4.1节中已经确认BWRS在计算中的优势，故在此不再使用其他状态方程求解LNG或天然气焓值。综上所述，软件在对LNG、天然气物性计算中具有较高的精度，能够较好地满足LNG接收站的物性计算需求。

5 计算实例

下面以大连LNG接收站常用天然气组分，即表4中的组分2为例，计算不同工况的LNG或NG物性。但是，因为计算物性较多，所以只列举出几个特殊物性用以实例计算。

(1) 卸船完成后，吹扫目标温度。卸船完成后，对码头各液相臂所在管线的吹扫，需保证管线内无液体，吹扫工作方完成。而吹扫时的最高压力为500 kPa(G)，所以此压力下的泡点温度即为其目标温度，通过软件计算为-133.441 ℃。

(2) 储罐内及高压泵出口的LNG密度，外输计量条件下的天然气密度及高位发热量计算。LNG储罐压力一般为20 kPa(G)、温度为-159 ℃，软件计算密度为444.138 kg/m3；高压泵出口压力为10 MPa(G)、温度为-140 ℃，软件计算密度为423.404 kg/m3；外输计算条件为压力0 kPa(G)，温度为20 ℃，软件计算密度为0.704 91 kg/m3，高位发热量为38.789 MJ/m3。

(3) SCV效率的计算需要先求解出入口LNG的总焓值和出口NG总焓值；之后求出二者焓差；然后计算出燃料的总发热量；最后用焓差除以发热量即可求出SCV的效率(由于NG出口压力与LNG入口压力非常接近，因此以LNG入口压力作为LNG出口压力)。表7中列出了SCV效率计算所需的参数，通过这些参数计算出SCV的效率为95.23%。

表7 SCV效率计算所需参数

6 结 语

软件以BWRS方程为基础，计算出LNG和NG的密度、比热、焓和熵，同时得出天然气的压缩因子和绝热降压后温度；而发热量则是根据GB/T 11062-1998标准中的数据建立适合的关系式求得；为了满足LNG接收站泡点需求，通过数据拟合求解出了接收站常用的一些LNG(NG)组分所对应的泡点温度和压力。通过误差及实例计算可以看出，软件具有使用简单、运算精度高等特点，能满足LNG接收站常规工况物性计算的需求。

参考文献

[1] 吕俊，张昌维，傅皓. LNG接收站BOG压缩机处理能力计算及选型研究[J]. 化工设计，2011，21(1)：14-16.

[2] 张艳春,于国杰,杜国强,等.LNG大型储罐加强圈设计[J].石油与天然气化工,2011,40(5):433-436.

[3] 陈雪,马国光.流程参数对LNG接收终端蒸发气再冷凝工艺流程性能的影响[J].石油与天然气化工,2008,37(2):100-104.

[4] 付子航.LNG接收站蒸发气处理系统的动态设计计算模型[J].天然气工业，2011，31(6)：85-88.

[5] 洪丽娜，陈保东，李庆杰，等. P-R 方程在天然气热物性计算中的应用[J].辽宁石油化工大学学报，2008,28(2)：48-52.

[6] 喻西崇，赵金洲，邬亚玲,等.PVT状态方程的选择与分析[J].油气储运，2001,20(9)：24-27.

[7] 刘璐，刘宝玉，李少华,等.LNG热物性计算[J].当代化工，2010,39(6)：696-698.

[8] 顾安忠，鲁雪生，汪荣顺,等.液化天然气技术[M].北京：机械工业出版社，2003.

[9] 郭天民，阎炜，濮芸辉,等.多元气-液平衡和精馏[M].北京：石油工业出版社，2002.

[10] 苑伟民.修改的BWRS方程[J].石油工程建设，2012,38(6)：9-12.

[11] 北京石油设计院.石油化工工艺计算图表[M].北京：烃加工出版社，1985.

[12] 罗焕章.石油化工基础数据手册[M].北京：化工出版社，1984.

[13] 彭世尼，陈建伦，杨建.天然气绝热节流温度降的计算[J].煤气与热力，2006，26(1)：1-4.

[14] 张鸿鹏，李颜强.门站调压节流引起管道低温的分析[J].煤气与热力，2009,29(1)：B1-B4.

[15] 董正远，肖荣鸽.计算天然气焦耳-汤姆逊系数的BWRS方法[J].油气储运，2007,26(1)：18-22.

[16] 中国石油天然气总公司.GB/T 11062-1998 天然气发热量、密度、相对密度和沃伯指数的计算方法[S].北京：国家质量技术监督局，1998.

[17] 魏凯丰，张作群，牛滨.天然气混合气体发热量的计算[J].哈尔滨理工大学学报，2005,10(6)：109-116.

[18] 孙兰义.化工流程模拟实训—Apsen Plus教程[M].北京：化学工业出版社，2012.

[19] 陈杰.MATLAB宝典[M].北京：电子工业出版社，2011.

[20] 张运刚.从入门到精通—工业组态技术与应用[M].北京：人民邮电出版社，2008.