模块化神经网络集成方法研究

刘文波，李来鸿

(1. 胜利油田电力管理总公司，山东 东营 257200；2. 胜利油田电力管理总公司 河口供电公司，山东 东营 257200)

自1991年Jacobs[1]提出模块化神经网络MNN(Modular Neural Network)以来，MNN已经在控制、建模等领域得到了广泛的应用。MNN采用“分而治之”的思想，将复杂问题分解为若干独立的子问题，对于每一子问题构建相应子网络。对于给定输入，MNN只选择一个子网络对其进行处理，子网络的输出即为整个网络的输出。“分而治之”的策略有效地降低了神经网络的复杂程度，解决了单一神经网络在面对复杂问题时存在的结构设计困难、学习速度慢、泛化性能差等诸多问题。但是，传统MNN的每个子网络只处理独立的样本空间，这使得MNN的子网络功能之间出现了明显的边界，从而MNN对于边界输入的处理精度较低。

针对MNN的缺点，一些学者提出在MNN中引入集成学习的思想[2-5]，理论和实践的研究均证明[6]集成学习可以有效地提高神经网络的逼近精度和泛化能力。2007年，Gao等[4]采用类模块划分方法将一个n分类问题分解为n个2分类问题，其中，每个子网络除对本网络的样本子空间进行训练外，还对相邻子网络样本子空间的样本进行训练。2009年，Mario[5]也采取了类似的方法解决图像识别问题。在子网络整合中两者都采用了集成的方法。对于任一给定输入，与该输入相邻的所有子网络均参与信息的处理。上述方法在总体“分而治之”的基础上，通过局部的“集思广益”，有效地提高了神经网络的性能。但是，上述方法中MNN的每个子网络都对所有相邻区域的样本进行训练，这使得每个子网络训练的样本空间增大，势必会增大子网络的规模。此外，2002年，Zhou等[6]对集成学习问题进行了研究，提出了“Many could be better than all”的思想，并证明从与输入相邻的所有子网络选择部分子网络进行集成可以获得更好的性能。所以，对于一个输入信息，如何从与输入相邻的所有子网络选择部分合适的子网络对其进行处理，针对各子网络的输出如何进行整合仍然是MNN尚未解决的问题。

笔者提出了一种基于距离测度和模糊决策的子网络选择方法，并提出了基于样本空间重构的方法来优化子网络的输出权重。上述方法实现了MNN的在线自适应集成。

1 模块化神经网络

一般的MNN结构如图1所示。其主要由任务分解、子网络、输出整合三个部分组成。

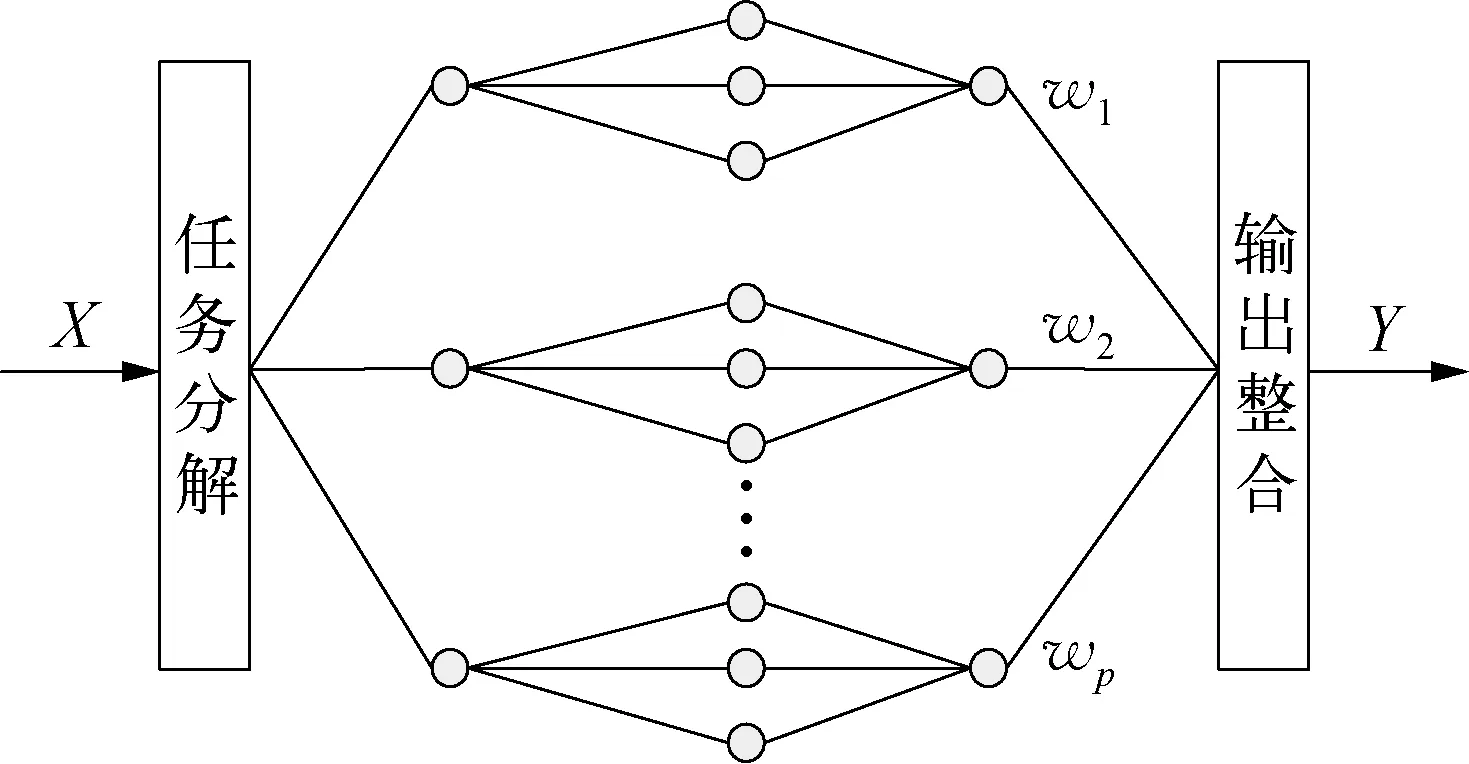
图1 MNN结构示意

离线学习时，任务分解实质是将整个输入样本空间按照一定规则划分为若干子样本空间[7](由于样本集的模糊性，各子样本空间可以存在一定程度的交叠)。对于在线输入信息，任务分解模块需首先判断该输入属于哪个子样本空间，然后将输入信息送入相应子样本空间对应的子网络进行处理。子网络的个数与子样本空间个数相同。

输出整合是将被选择进行信息处理的子网络的输出进行合并。一般MNN的整合采用线性整合方式[4-6，8]，图1所示的模块化神经网络的总输出为

(1)

式中：P——子网络个数；yi——第i个子网络(记为NETi)的输出；wi——NETi的权重，满足∑wi=1，且0≤wi≤1，i=1， …，P。

对于在线输入，传统的MNN子网络选择方法(记为SM1)只选择一个子网络(假设为NETs)，对其进行处理，即有w=1，wi， i≠s=0。而文献[4-5]提出的网络选择方法(记为SM2)则选择所有与输入相邻的子网络对输入信息进行集成处理，即对于所有与输入相邻的子网络，有0≤wi≤1，而与输入不相邻的子网络，wi=0。

实际上，MNN的子网络选择与输入点位置有关。如图2所示，当输入位于A点时，子网络1对输入进行单独处理即可取得较好的效果。而当输入位于B，C点时(样本子空间的交界处)，任何单一子网络对该点的处理能力均有限。按照集成学习理论，选择与B，C点临近的部分子网络对其进行集成处理可以获得较好的效果。因此，笔者提出了一种根据输入信息位置动态选择参与信息处理的子网络方法SM3。采用该种方法，每个子网络只对相应子空间及其某一邻域的样本进行训练。对于任一输入信息，SM3的选择的子网络个数介于SM1和SM2之间，因而该方法可以使MNN具有更强的自适应能力。

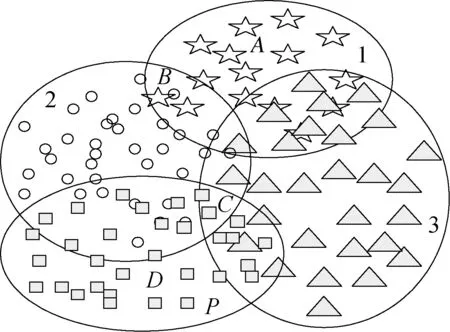
图2 样本分割示意

综合上述分析，SM3的集成问题主要有两个： 如何根据输入信息动态选择参与信息处理的子网络；如何确定参与信息处理的子网络的权重(对于未被选择的子网络，其权重wi=0)。

2 SM3的动态集成方法

2.1 子网络选择

子网络选择的实质是针对给定输入从所有子网络中选择出最适合处理该输入的子网络集合。文献[4-5]采用局部全集成策略，易导致子网络规模过大。文献[8]提出了一种基于距离测度选择子网络的方法。对于给定输入Xs，计算该输入与NETi对应样本中心的距离测度di，与输入距离测度小的子网络更适合处理该输入。其做法是设定一阈值K，若di≤K，则NETi被选择，否则，NETi被剔除。文献[9]提出了一种首先用遗传算法优化权重，然后剔除对权重小于某一阈值的子网络。相比文献[4-5]的方法，文献[8-9]的方法更为灵活，但文献[8-9]的方法需要凭经验确定阈值K，K值选择不合理，会引入差的子网络或剔除好的子网络，从而达不到通过集成处理提高性能的目的。此外，对于不同的输入，文献[8-9]中阈值K是固定的，使得神经网络对不同输入的适应能力较差。

针对上述问题，笔者提出了一种基于距离测度和模糊决策的子网络选择方法，该方法不需要确定阈值，并且子网络选择具有较强的自适应能力。

设V={V1， …，VP}为样本分类中心，令

di=‖Xs-Vi‖/dai

(2)

其中，

(3)

式中：dai——第i个样本子空间的样本平均距离；di——输入Xs对NETi的相对距离测度；Ni——第i个样本子集的样本数。

显然，对于输入Xs，相对距离小的子网络应首先被选择。而相对距离大的子网络不仅不能提高网络性能，反而会降低网络精度，因此，网络选择过程实质是保留相对距离小的子网络，同时剔除相对距离大的子网络。按照这种思想，子网络的选择即转化为输入对子网络的相对距离判别问题。

首先将Xs对所有子网络的相对距离测度按照下式进行归一化处理：

(4)

其中，ui∈[0 1]， ∑ui=1。

令相对距离测度的模糊集A={很小(VS)，小(S)，中等(M)，大(B) }。ui对A的模糊隶属函数曲线如图3所示。

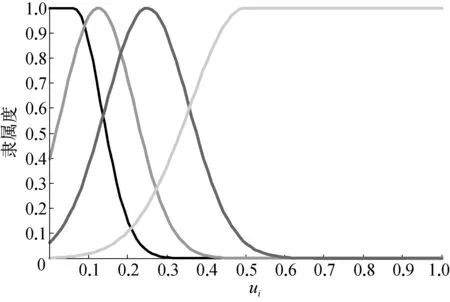
图3 ui的隶属度曲线(P=4)

ui的大小可以反映输入Xs与NETi的距离。若ui∈{VS}，则说明Xs距离NETi很近，则子网络NETi应该被选择用于处理Xs；若ui∈{B}，则说明Xs距离NETi很远，则对于Xs来说子网络NETi应该被剔除。子网络选择的算法如下：

Step1： 对于输入Xs，通过式(2)～(4)计算输入Xs对相应子网络的ui值。

Step2： 根据图3所示的隶属函数曲线，计算ui相对于A各模糊子集的隶属度。

Step3： 通过最大隶属度法判断ui属于哪个模糊子集，然后按照从VS到B的顺序选择属于同一集合的子网络进行集成。

Step3中，首先选择ui∈{VS}的子网络进行集成，其余的子网络均被舍弃。若ui∈{VS}的子网络不存在，则选择ui∈{S}的子网络，否则选择ui∈{M}的子网络。

设置隶属函数中模糊子集{VS，S，M，B}的中心点分别为1/(4P)， 1/(2P)， 1/P， 2/P，并且满足：ui<1/(4P)，ui∈{VS}的隶属度为1；ui> 2/P，ui∈{B}的隶属度为1。由于∑ui=1，因而所有的ui不会同时满足ui>1/P，即ui∈{VS，S，M}对应的子网络不会为空集。由于step3中子网络的选择顺序为VS到B，所以ui∈{B}的子网络不可能被选择。

2.2 子网络整合权重的确定

对于输入Xs，设被选择的子网络为NETks(k=1， …，m)，m为被选择的子网络个数。网络的总输出为

(5)

式中：wk——子网络NETks的权重；yks——NETks对Xs的输出。权重确定问题实质上是为被选择用于信息处理的子网络集合选择一组最佳的值。Zhou等[6，9-10]提出了一种基于遗传算法的权重优化方法(GASEN)，由于遗传算法寻优速度较慢，因而GASEN方法不适合参数的在线优化。此外，由于Xs为在线输入，其目标值未知，因而很难构造遗传算法的适应度函数。王攀等[8]提出了一种基于距离测度的权重确定方法，这种方法使得与输入距离近的网络获得更高的权重。Sun等[2]提出了一种将输出误差倒数作为权重的方法。这两种方法本质上属于一种经验方法，无法保证权重的最优性。针对上述方法的不足，笔者提出了一种基于样本空间重构的权重优化方法。

对于输入样本空间，若两个样本的距离越近，则这两个样本的相似性越强。对于输入Xs，参与信息处理子网络为NETks(k=1， …，m)，则用该子网络集合对于Xs的某一微小邻域的输入进行处理也是合适的。

设δ为Xs的一个微小的邻域，其包含的样本为{X1， …，XK}，相应目标值为{t1， …，tK}，K为δ邻域包含的样本数，所有样本均满足：

‖Xi-Xs‖≤δ。

由于δ很小，因此该K个样本均可由NETks(k=1， …，m)处理。将δ空间中的样本输入到神经网络，网络泛化误差为

(6)

其中，Yj为神经网络对Xj的输出：

显然，权重向量w的选择应使式(6)最小化。因此，上述问题可以用一个约束优化模型描述：

minJ(J=MSE)

(7)

由于δ邻域中样本的目标值tj是已知的，因而权重的确定问题转化成一个如式(7)约束优化问题，其未知数为w=[w1， …，wm]T。该问题可以用动态规划的方法求解。

上述方法通过重构一个Xs的邻域δ，通过δ邻域内已经学习过的样本信息将权重优化问题转换成了一个约束优化问题。但是，当样本点较为稀疏或δ邻域过小时，可能会出现K=0的情况(δ邻域内不包含样本点)，此时w不能用式(7)所表示的模型优化。出现这种情况时，w可以采用文献[8]的方法确定。在实际应用中，可以人为给定一个样本个数最小值KF，当K≤KF时，子网络的w由下式确定：

(8)

式(8)赋予与输入距离小的子网络以较大的权重。

3 仿真实验

首先以一维“SinC”函数(二维Mexican Hat)[9-10]逼近为例对网络的逼近能力进行研究，“SinC”函数表达式为

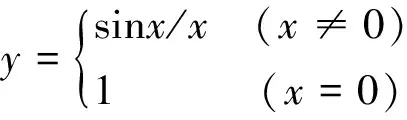
其中，x∈[-10， 10]，在区间[-10， 10]内随机产生1000个训练样本和200个测试样本，样本中不含噪声。取P=5(子网络采用BP网络，为方便起见，每个子网络隐层节点数取为相同)，采用Fuzzy C-means技术将1000个样本分为10组，各组样本之间存在一定程度的交叠。分别采用SM1(只选取一个子网络参与信息处理)、SM2(选择与输入相邻的所有子网络参与信息的处理)、SM3(笔者提出的子网络选择方法及权重确定方法)、SM4(文献[8]提出的基于距离测度和阈值选择子网络和确定子网络权重的方法)进行逼近性能测试。SM3方法的拟合曲线如图4所示。

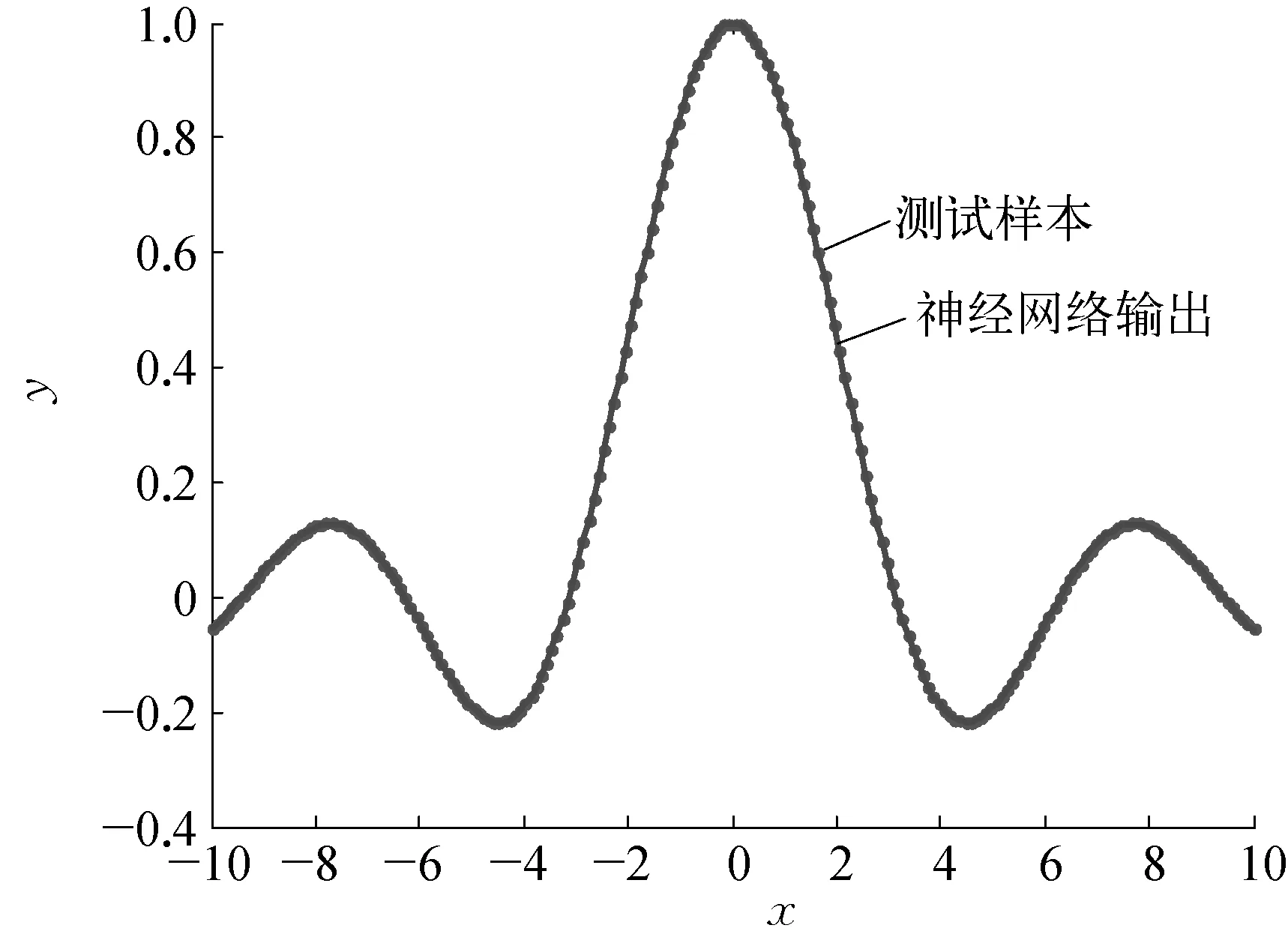
a) 无噪声

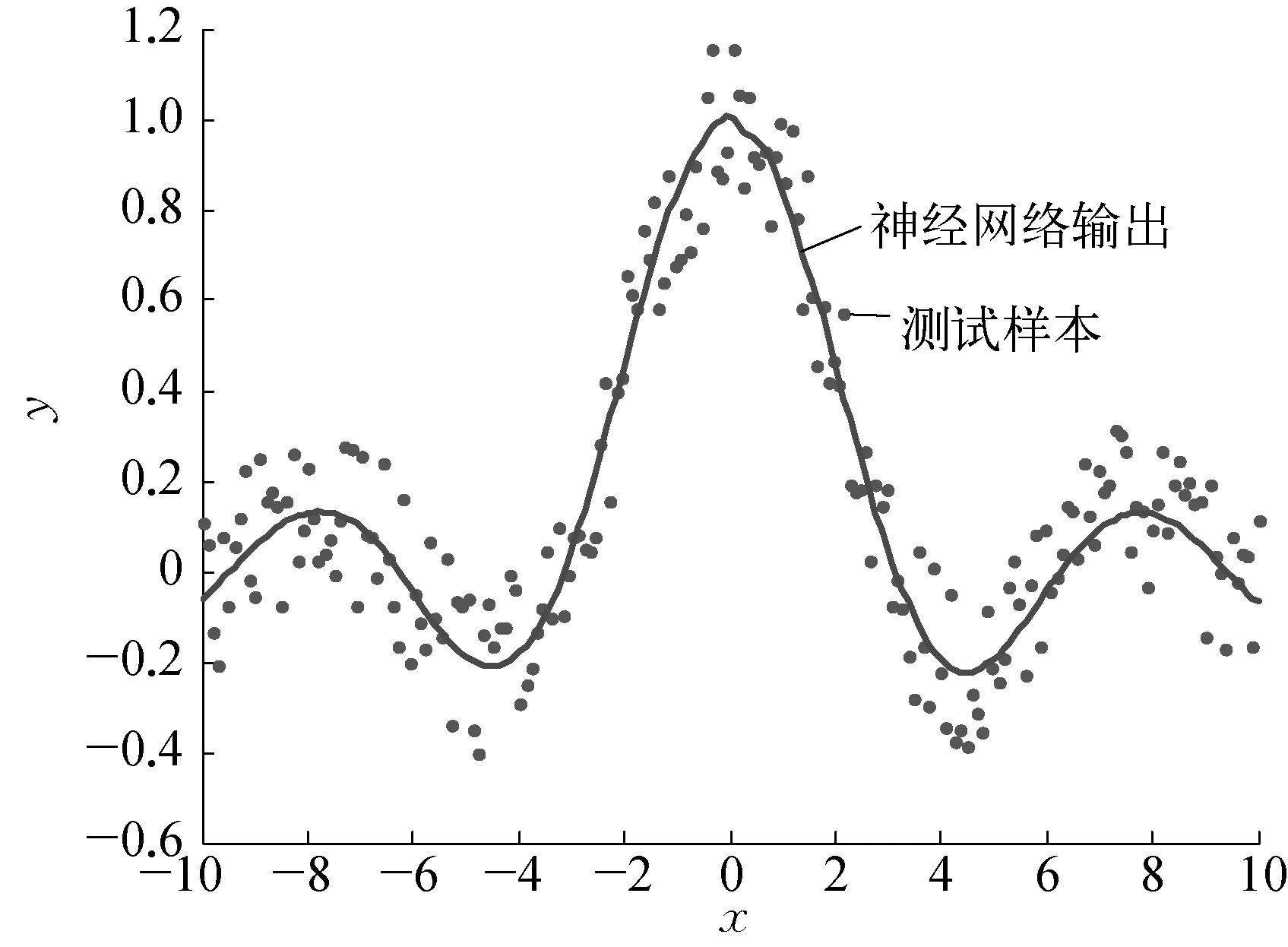
b) 有噪声

四种网络在隐层节点个数不同情况下的均方误差见表1所列。从表1可以看出，在隐层节点数较少的情况下，SM1， SM3， SM4方法的逼近精度高于SM2方法，这是由于SM2方法采用局部全集成策略，每个子网络都要对相邻的样本子空间实现映射，子网络映射范围较大。当隐层节点数较少时(子网络隐层节点数为3)，子网络映射能力不足，导致SM2的泛化误差较大。当隐层节点数与问题复杂度匹配时(子网络隐层节点数为4)，SM2的泛化误差明显减小。而SM1， SM3， SM4方法需要映射的样本子空间较小，实现映射所需要的子网络结构也较SM2简单，因而在子网络节点较少的情况下也可以获得较高的精度。在训练样本不含噪声的情况下，四种方法都可以达到较高的精度，但SM3在获得较低的泛化误差同时，还可以使网络保持较为简单的结构。

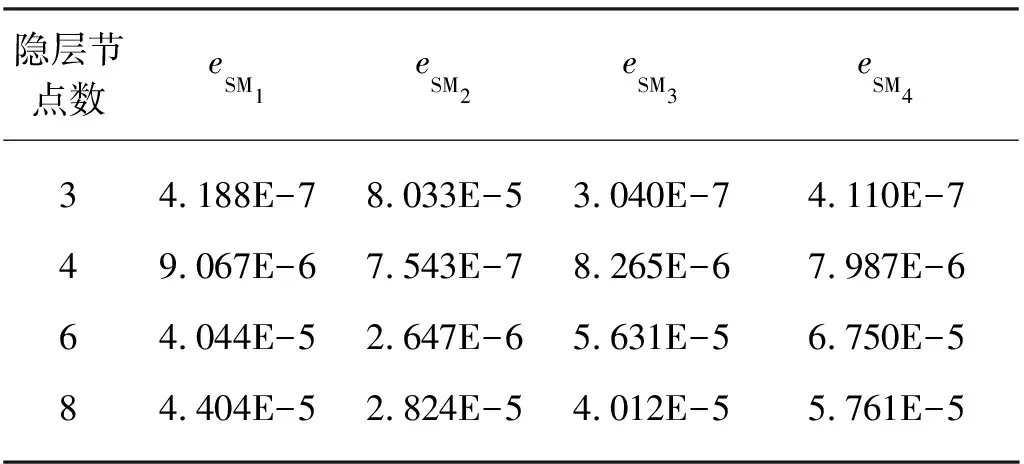
表1 网络的拟合误差(无噪声)

由于实际数据往往含有噪声，为了测试SM3在噪声下的泛化能力，在所有训练样本上附加取值范围为[-0.2， 0.2]的随机噪声。图4b)为SM3的拟合曲线。几种网络在隐节点数不同情况下的拟合均方误差见表2所列。

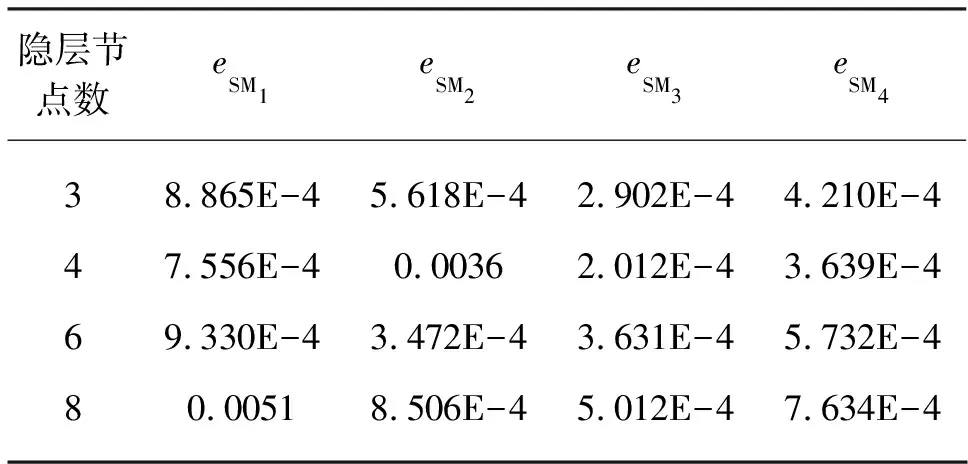
表2 网络的拟合误差(有噪声)

从表2可见，当训练样本含有噪声时，SM3的泛化误差明显小于SM1，这是由于SM3采用了集成学习的思想，降低了噪声的影响。在子网络隐层节点数较少的情况下，SM3的泛化误差明显小于SM2，与SM4相比，SM3的泛化误差相当，但是SM4方法的阈值需要经过多次测试才能得到较好的结果，而SM3则避免了此困难，因此，在结构的简单性、泛化能力及参数选择难度上，SM3优于其余三种方法。

接下来对SM3处理多维信息的能力进行测试，首先选择三维Mexican Hat函数(二维“SinC”函数)[11]：

仿真结果如图5所示：

SM3拟合的均方误差为5.132E-5，文献[11]也采用一种基于遗传算法的集成方法(GPCMNN)对该函数进行了测试，均方误差为9.613E-5，所以该方法在泛化能力存在一定优势。

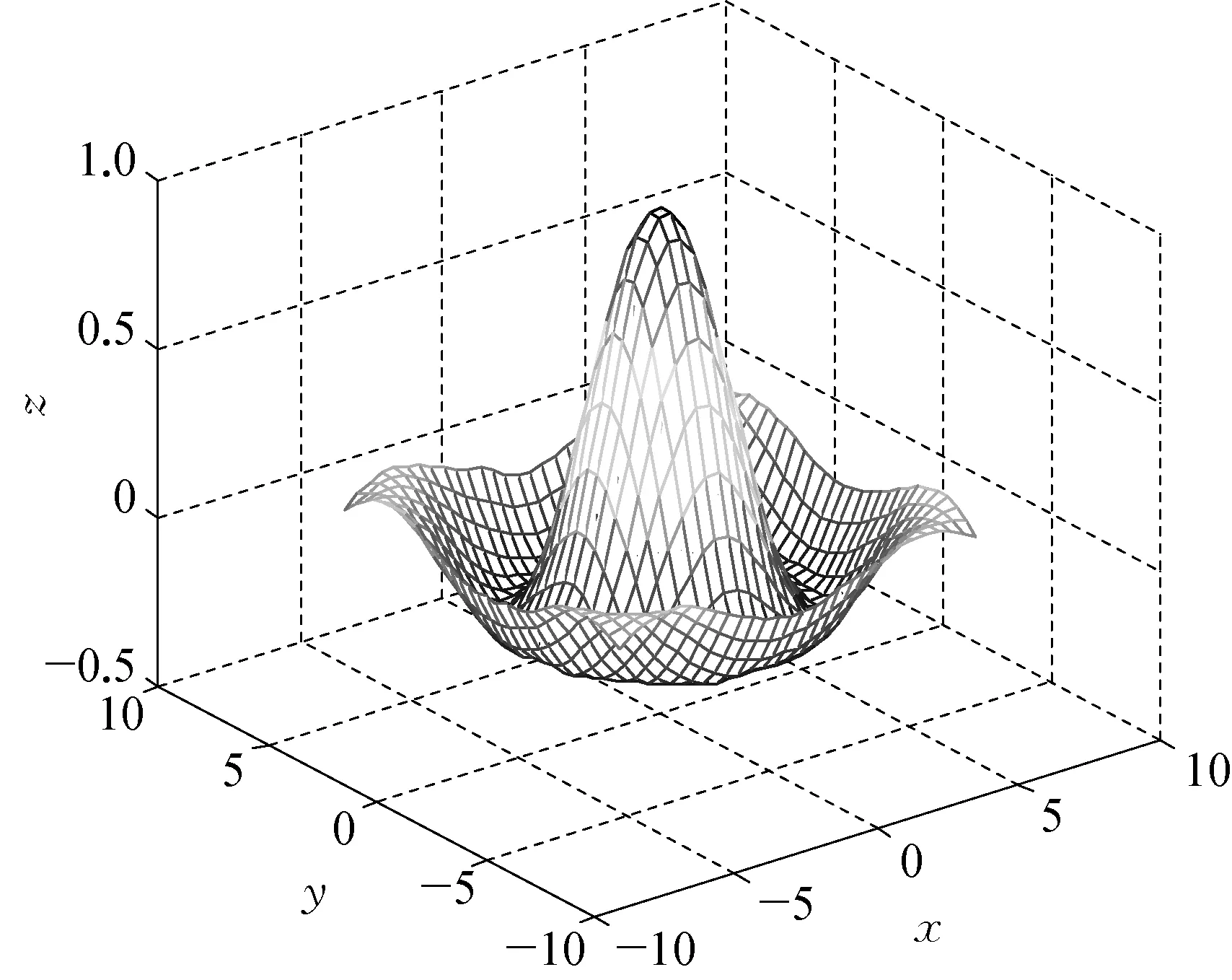
a) 拟合曲面

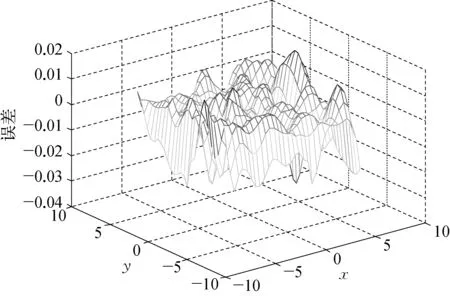
b) 误差曲面

进一步，对Friedman #1， Friedman #2， Plane 3个人工数据集进行测试(其中前两个数据集输入为5维，后一个为2维)。3种人工数据集的生成方式见文献[10]，文献[10]采用了集成神经网络(ENN)进行测试。采取不同集成方法时神经网络测试均方误差见表3所列。由表3可见，模块化网络的均方误差均比文献[10]的均方误差要低，说明MNN“分而治之”的思想在解决复杂回归问题方面具有一定的优势。而在3组数据集实验中，SM3的测试误差最小，说明本文的子网络选择方法和权重优化方法是有优势的。

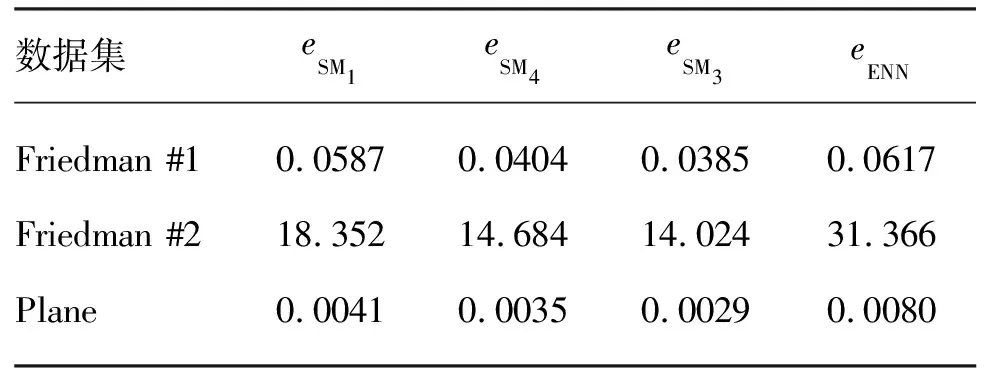
表3 网络的测试误差

4 结束语

在“分而治之”的基础上，融合了“集思广益”的思想，使神经网络结构大幅简化的同时，提高了神经网络的性能。对于给定输入信息，采用模糊决策的方法实现处理该信息的子网络集合的选择，避免了人为设定阈值的困难。通过重构输入信息的邻域样本空间，将权重的优化问题转化为一个约束优化问题，从而可以使用动态规划等多种方法实现权重的优化。大量的仿真实验表明，笔者提出的MNN集成方法在结构的简单性、泛化能力、参数选择的难度等方面与ENN及其他的模块化网络集成方法相比具有一定的优势。

参考文献：

[1] JACOBS R A， JORDAN M A. Modular Connectionist Architecture for learning Piecewise Control Strategies [C]. America： Proceedings of the American Control Conference. 1991： 343-351.

[2] SUN Jianzhong， ZUO Hongfu， YANG Haibin. Study of Ensemble Learning-Based Fusion Prognostics [C]. Prognostics and Health Management Conference， 2010.

[3] GANGARDIWALA A， POLIKAR R. Dynamically Weighted Majority Voting for Incremental Learning and Comparison of Three Boosting Based Approaches [C].

Canada： Proceedings of International Joint Conference on Neural Networks. 2005.

[4] GAO Daqi. Class-modular Multi-layer Perceptions， Task De-composition and Virtually Balanced Training Subsets [C]. Florida： Proceedings of International Joint Conference on Neural Networks. 2007.

[5] MARIO G C A， WITOLD P， BEATRICE L， et al. Using Multilayer Perceptrons as Receptive Fields in the Design of Neural Networks [J]. Neurocomputing， 2009(72)： 2536-2548.

[6] ZHOU Zhihua， WU Jianxin， WEI Tang. Ensembling Neural Networks Many Could be Better Than All [J]. Artificial Intelligence， 2002(137)： 239-263.

[7] WITOLD P， GEORGE V. Granular Neural Networks [J]. Neurocomputing， 2001(36)： 205-224.

[8] 王攀，李幼凤.模块化神经网络的动态集成方法研究[J].系统工程与电子技术，2008，30(06)： 1143-1147.

[9] ZHOU Zhihua， WU Jianxin， WEI Tang. Combining Regression Estimators： GA-Based Selective Neural Network Ensemble [J]. International Journal of Computational Intelligence and Applications， 2001， 1(04)： 341-356.

[10] 王正群，陈世福，陈兆乾.并行学习网络集成方法[J].计算机学报，2005，28(03)： 402-408.

[11] 凌卫新，郑启伦，陈琼.基于梯度的并行协作模块化神经网络体系结构[J].计算机学报，2004，27(09)： 1256-1263.