后方交会模型病态问题分析与改善

刘新竹，康志忠

(中国地质大学(北京)土地科学技术学院，北京 100083)

后方交会模型病态问题分析与改善

刘新竹，康志忠

(中国地质大学(北京)土地科学技术学院，北京 100083)

病态性问题一直广泛存在于各种数据处理中。摄影测量学中的许多基本模型在有些条件下也容易使方程组产生病态，如在后方交会时加入自检校解算内方位元素等情况下易得到不稳定的解。主要介绍摄影测量中的一种基本模型——后方交会，以及病态性的基本概念、几何含义、危害性和几种改善算法。实验部分对后方交会中的病态问题进行研究，并利用岭估计及截断奇异值法进行改善分析，提高解算精度。

病态问题；后方交会；截断奇异值分解；条件数

测量学中的很多问题，经过归纳和分析最后都可以归结为解算方程组：将观测值带入模型中，通过测量平差的手段求得未知量的估计值。近些年来，随着空间科学技术的发展和人类社会生活模式的改变，人们对地理信息的需求也在发生转变，测量技术和测量手段也都发生了翻天覆地的变化，测量数据的处理过程变得复杂起来。而某些特殊情况下，系统对数据的微小扰动有非常强的敏感性，此时称系统为病态的[1]。如果平差模型的设计阵呈现病态，则法方程系数矩阵更加病态，使用最小二乘法虽然能够得到最优的线性无偏估计，保证在无偏的条件下方差最小，但这时的估计值偏离真实值的幅度变得很大，片面追求无偏估计已经不是最优答案。因此，对于病态问题，必须寻找其他方法来改善解的精度。

从20世纪60年代以来，数学界对病态问题的研究已经得到高度的重视，70年代末开始，国外学者不同领域对模型病态问题进行长期大量的研究。M.M.Lavrent’ev,V.G.Romanov在1986年对一些常见病态问题的原理和成因进行研究，并分析数学、物理中的一些病态性例子，为后人的研究和处理奠定一定的基础。国内一些专家也于80年代开始针对测量工程、岩土工程、土木工程等领域对病态性进行探究。王志中等于1988年从病态问题的实质和几何意义出发，给出评估方程病态的指标；在测量工程领域里，1987年郑肇葆在其文章中分析病态方程的表现，针对几种求解病态方程的方法进行对比。郭建锋在其硕士学位论文[1]中，详述病态性的成因和诊断，分析复共线性与其之间的关系，对病态性的本质进行深入的研究。叶松林在多篇文章中就矩阵奇异值分解法和广义岭估计对解算病态性问题的思想、途径、适用范围、工作量大小等方面进行论述，并实验证明其改善效果。

1 后方交会模型的病态性分析

1.1 后方交会模型概述

摄影测量中，描述每一个像点、摄影中心与对应地面点都满足位于一条直线上的关系的模型就是共线条件方程

(1)

单像空间后方交会是指利用地面控制点及其在像片上的像点，确定1张像片外方位元素，恢复其空间姿态的方法。进行解算的理论基础就是对共线条件方程的线性化及泰勒公式展开，得到如下误差方程式

(2)

式中：vx，vy是像点坐标的改正数，(x)，(y)为函数的近似值，是将外方位元素初值XS0，YS0，ZS0，φ0，ω0，κ0代入共线方程中所得到的值。

将像点坐标及对应地面点坐标代入方程，并把误差方程式化为间接平差V=AX-l的形式，运用最小二乘法进行平差计算x=(ATA)-1ATl，最后由逐步趋近的方法进行迭代，得到外方位元素的准确值。

1.2 后方交会模型病态性分析

在后方交会中，由于地形的特殊性常常会导致模型出现病态问题。当选择的控制点处于近似的水平高度上，或近似分布于同一斜面上，所组成的方程组中就较容易存在复共线关系。在实际测量中，模型本身构造的优劣、解算方法的不当、观测时图形的几何构型较差以及过度参数化都有可能导致病态问题的出现，从而导致解的失真。

假设存在理想状态，如图1所示。

图1 理想情况下求解外方位元素

已知数据设定为：相机主距f=150 mm，像片大小为23 cm×23 cm，且呈水平，像平面坐标系x轴与地面坐标系X轴在竖直面平行；航高为

150 m，摄影中心的准确坐标为(0，0，150)，此时外方位角元素真实值为(0,0,0)。根据相似关系，假设像片上有4个控制点的像点和地面坐标分别为

(50,50)，(-50,50)，(-50,-50)，(50,-50)，单位为mm;

(50,50)，(-50,50)，(-50,-50)，(50,-50)，单位为m。

对像点坐标和地面点坐标真实值分别加入0.001 mm、0.005 m的随机误差，用最小二乘方法对线性化之后的平差模型进行解算，结果如表1所示。

表1 理想情况下模拟实验结果

表1中线元素的结果偏离真实值较大，可见该模型在选点均匀、误差合理的情况下解算结果仍不理想，说明模型本身的构造就存在不稳定性，易出现病态问题。

另外,在相机自检校的过程中，把内方位元素x0,y0,f当作未知参数，利用多余观测对内外方位元素同时开放求解，也易出现最小二乘解不稳定的情况，本文将在实验部分针对这种情况作详细阐述。

2 病态问题的基本原理

2.1 病态性原理概述

对于线性方程组

(3)

由最小二乘理论可得到法方程

(4)

(5)

(6)

将变得很大；在这种情况下求解得到的值在数值上是极不稳定的，观测值或是系数矩阵的微小变化很可能引起解的巨大波动，解的精度和准确度很差，这样的模型称其存在病态问题。

2.2 病态问题的诊断方法

条件数指标是在各领域病态性研究中相对来说最成熟的衡量指标。

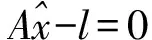
(7)

那么在数值上，称

(8)

被称为法矩阵N的条件数，λ1，λn表示N矩阵最小、最大特征值。

通过几十年的研究，总结出用条件数评价方程组病态程度的量化标准[2-3]：

1)条件数小于100可以认为没有病态问题；

2)条件数在100～1000之间认为存在中等程度的病态；

3)条件数超过1000认为存在严重病态性。

用条件数法诊断病态性的优势在于它运用一个相对的数值代替判断特征根最小值“很接近于0”这种模糊的说法，度量法方程系数阵特征根的大小分散程度，判断起来也较为方便。

3 病态问题的改善算法

3.1 岭估计法

(9)

3.2 奇异值分解法

(10)

式中：U，V为正交矩阵，ui，vi为U，V的第i列，S=diag([σ1，σ2，…，σt])为A的奇异值按从大到小排列的对角阵。该模型的广义逆解为

(11)

通过计算和推导可以得到，大部分情况下奇异值分解算法和最小二乘法是等价的，只是将设计矩阵表达成谱分解的形式[4]。而在实际计算中，分解得到的奇异值矩阵S会有很小的奇异值，这样直接对S求逆会产生极不稳定的解。而观测值的噪声是不可避免的，导致得到的X的估计值与准确值相差很大。若想达到减小均方误差的目的，需要去掉那些较小的奇异值或者进行修正，以此来达到提高可靠性的目的。

3.3 截断奇异值分解法

针对设计矩阵中奇异值存在接近于0的较小值、使均方差趋近很大的这种情况，一种比较直接的改进方法就是将那些较小的奇异值舍去，来改善模型的病态程度。假设截断后t-k个奇异值(即保留前k个奇异值)，由式(12)可以推得X的估计值

(12)

例如图1 的模拟实验中，利用截断奇异值分解法就可以得到外方位元素准确的解：线元素为(0,0,150)，角元素为(0,0,0)，精度大大提高。

3.4 改善方法参数的选取

选取岭参数及截断参数最常使用的方法就是L-曲线法，即在权衡残差与解的图像曲线中，选择拟合曲线上曲率最大点的k值作为岭参数或截断参数(有时也可以选取L曲线上到原点O最短距离的点的参数作为合理值)。但有时得到的参数会呈现均匀减小，曲线拐点不明确，从而造成参数不易选取或带有较大的主观性。

4 实验与分析

主要针对后方交会自检校部分利用模拟数据进行实验，并用前文提到的改善方法求解，比较其精度相对于最小二乘解是否有提高。

实验数据由三维激光扫描仪实测地面点坐标模拟得到,如表2所示。

模拟数据的处理方法为：将7个地面点坐标设为真值，扫描仪内测定的外方位元素值作为真实值，由此解算像素点坐标真实值；再给地面点坐标、像素点坐标加入随机误差(像点随机误差为0.3个像素，地面点为5 mm)，由此解算的外方位元素与设定的真实值对比如表3所示。

表2 实测像点与地面点坐标

表3 3种方法解算后方交会模型结果

表3所示为对3种方法解算外方位元素的结果与真实值作差进行对比。该模型的法方程系数矩阵条件数K=3.046 7×1011，属于严重病态，此时最小二乘解与真值相比偏离已较大。对岭参数进行不同的取值，得到的岭估计解与最小二乘结果基本一致，无法从根本上改善法方程的病态性。而使用截断奇异值法将9个特征根中后3个数量级相同的较小奇异值去掉后，得到相对于真实值较为近似的解。实验证明截断奇异值分解法可以有效改善后方交会模型中病态问题解的可靠性和准确性。

5 结束语

简要介绍摄影测量学中的一种基本模型——后方交会，阐述病态性产生的原理，以及两种数学上常用的改善病态问题的方法，并针对后方交会的具体模拟数据进行实验和病态性分析。实验结果显示：在地面摄影测量后方交会中，截断奇异值法能更大程度地改善法方程系数矩阵的病态性，有效地提高估计值的准确度和精确度，得到更优解。

[1]郭建锋.测量平差系统病态性的诊断与处理[D].郑州: 信息工程大学,2002.

[2]陈希孺,王松佳.近代回归分析: 原理方法及应用[M].湖北：安徽教育出版社,1987.

[3]卢波.病态问题的奇异值分解算法与比较[J].测绘信息与工程,2011,36(4): 19-22.

[4]归庆明,郭建锋,边少锋.基于特征系统的病态性诊断[J].测绘科学,2002,27(2): 13-15.

[5]叶松林,朱建军.矩阵奇异值分解与广义岭估计及其在测量中的应用[J].中国有色金属学报,1998,8(1): 160-164.

[6]王振杰,欧吉坤.一种新的病态问题奇异值修正方案及其在大地测量中的应用[J].自然科学进展，2004(6).

[7]付玉立,李全海.病态问题中奇异值修正法初探[J].海洋测绘,2011,31(2): 42-44.

[8]KLINGER A.Approximate Pseudo Incerse Solutions to Ill-Conditioned Linear Systems [J].Journal of Optimization Theory and Applications,1968,2(2): 117-124.

[9]TIKHONOV A N,ARSENIN V Y.Solutions of Ill-Posed Problems[M].New York: Wiley & Sons,1977.

[10]郑肇葆.摄影测量中病态方程求解问题——数学规划在摄影测量中应用之二[J].测绘学报,1987(3).

[11]张永军,吴磊,林立文,等.摄影测量中病态问题的条件数指标分析[J].武汉大学学报: 信息科学版,2010,35(3): 308-312.

Analysis and optimization of ill-posed model in space resection

LIU Xin-zhu,KANG Zhi-zhong

(School of Land Science and Technology,China University of Geosciences,Beijing 100083,China)

Ill-posed problem widely exists in data processing.Many models in photogrammetry can easily cause ill-posed equations under some conditions.For example,adding self-calibration in resection is easy to obtain unstable solutions of orientation elements.It presents a basic model of photogrammetry and space resection.It also presents the basic concept of ill-posed condition,as well as the harmfulness and several algorithms to improve the results.The experiments mainly aim at the ill-posed model in resection,with ridge estimate and truncated singular value decomposition method to improve the accuracy.

ill-pose porblem; resection; TSVD; condition number

2013-12-10

刘新竹(1991-)，女，硕士研究生，研究方向：摄影测量与遥感方向.

P232

A

1671-4679(2014)03-0015-04

郝丽英]