基于点云数据三维重建方法的研究
2014-09-07纪志浩于明旭
纪志浩,于明旭
(1.徐州市三联测绘服务有限公司,江苏 徐州 221116;2.江苏建筑职业技术学院,江苏 徐州 221116)
基于点云数据三维重建方法的研究
纪志浩1,于明旭2
(1.徐州市三联测绘服务有限公司,江苏 徐州 221116;2.江苏建筑职业技术学院,江苏 徐州 221116)
由于三维激光扫描仪采集的点云数据是离散的,这些离散的点云数据由于分辨率有限,缺少灵活性,导致无法满足对实际场景重建出具有几何精确性的模型。为解决上述问题,用Delaunay三角化方法构造网格逼近物体的三维表面模型,把离散的点云数据连续化生成表面模型来模拟场景,实验证明该方法有效。
点云数据;Delaunay三角化;Voronoi图;曲面模型;三维重建
依据离散点云数据集与重建三维曲面之间关系,三维重建分为逼近法和插值法两大类。依据重建曲面的表现形式,可将重建分为以下几种:网格重建、参数重建、隐式重建、变形重建和细分重建。
离散点云数据重建实际场景三维表面模型就是将离散点连续化,其本质是进行插值。利用离散点数据构建网格有不规则三角网和不规则四边形,不规则三角网TIN与四边形格网模拟表面相比具有如下优点:一是在分辨率相同的情况下,TIN模型占用存储空间少,构网时间短,且表示复杂曲面精细度好。二是通过离散点组成的三角形,其几何算法最可靠,并且绝大部分软件、硬件的图形真实感反映系统运算的基本单元都是以TIN作为基础。基于上述特点,模拟场景表面模型最常用的方法是构建三角形网格,目前,Delaunay三角剖分方法是构建三角形网格中最为常用的方法。
1 Delaunay三角剖分
本文通过离散点集的Delaunay三角剖分实现重建实际场景的三维模型。为更好了解Delaunay三角剖分,首先介绍Voronoi图和三角剖分概念。
1.1 Voronoi图
Voronoi图是一个广泛应用的图结构。它是由连接两邻点直线的垂直平分线组成的连续多边形,是Delaunay三角剖分的基础,Voronoi三角形是Delaunay图的对偶图。
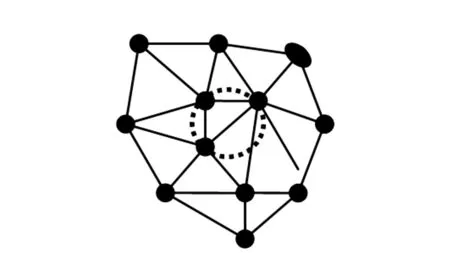
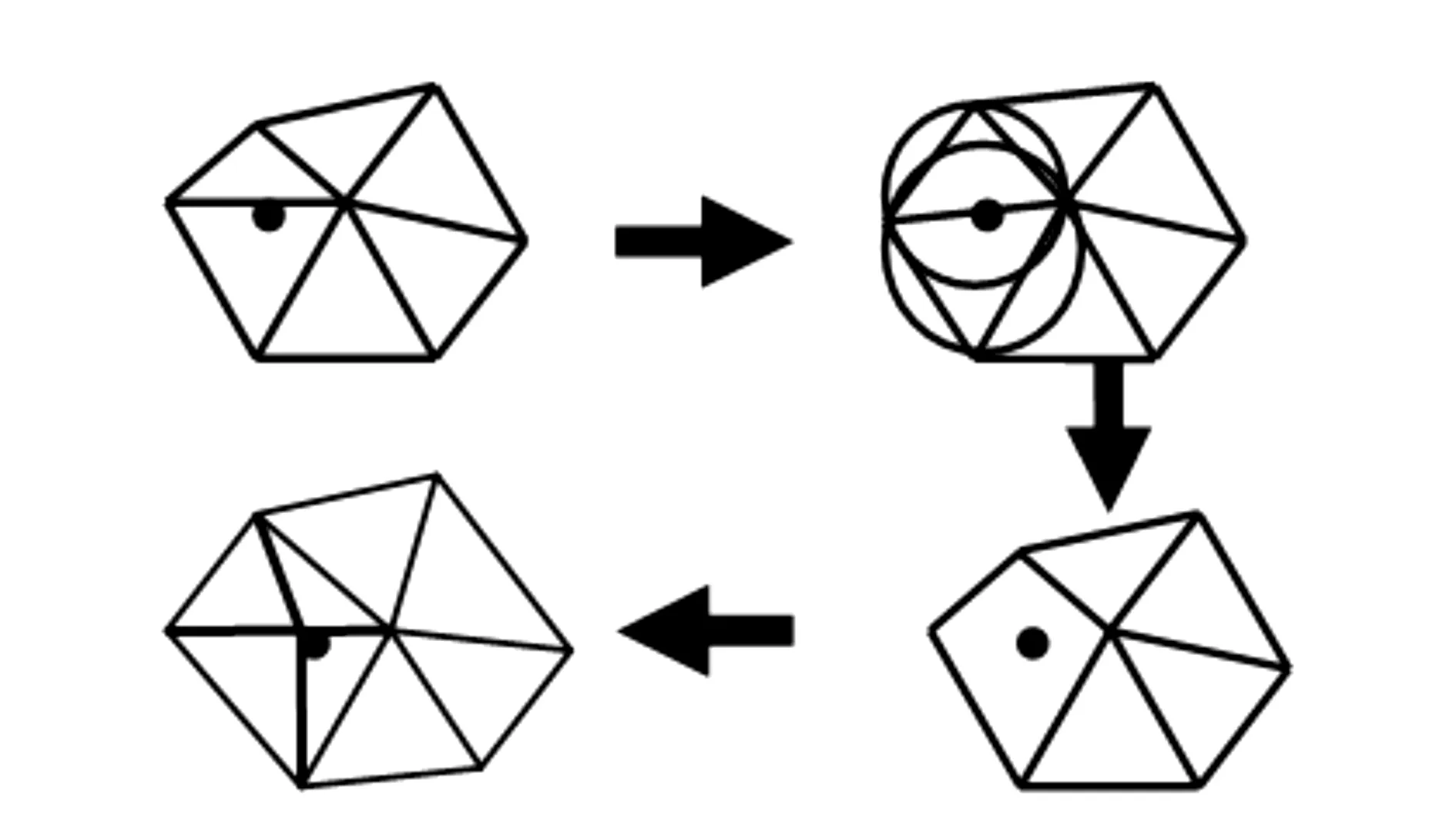
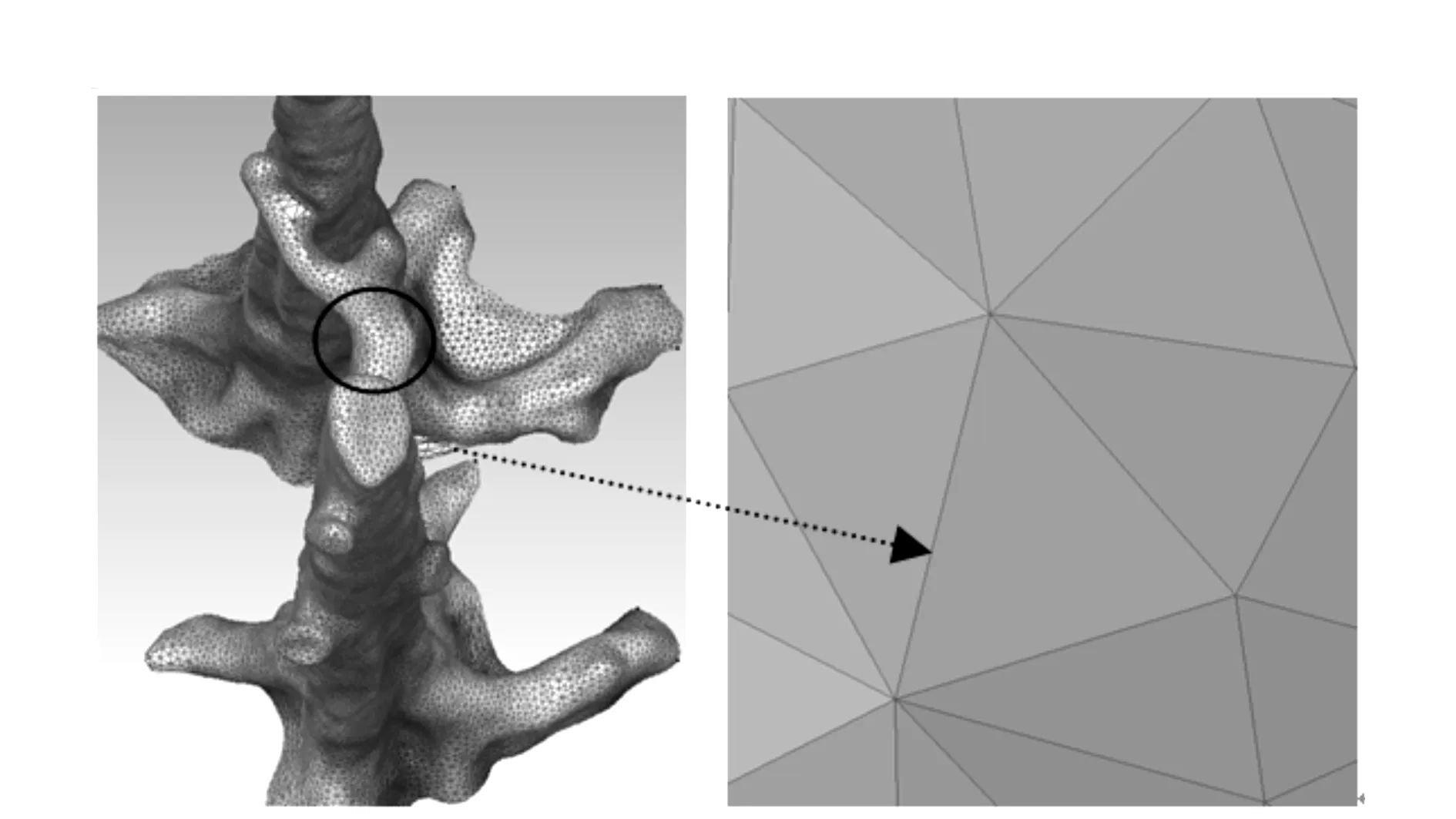
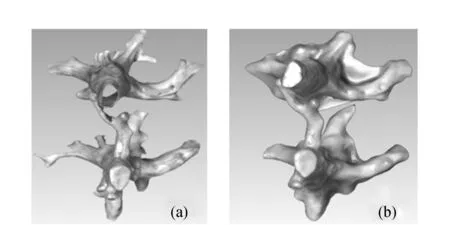
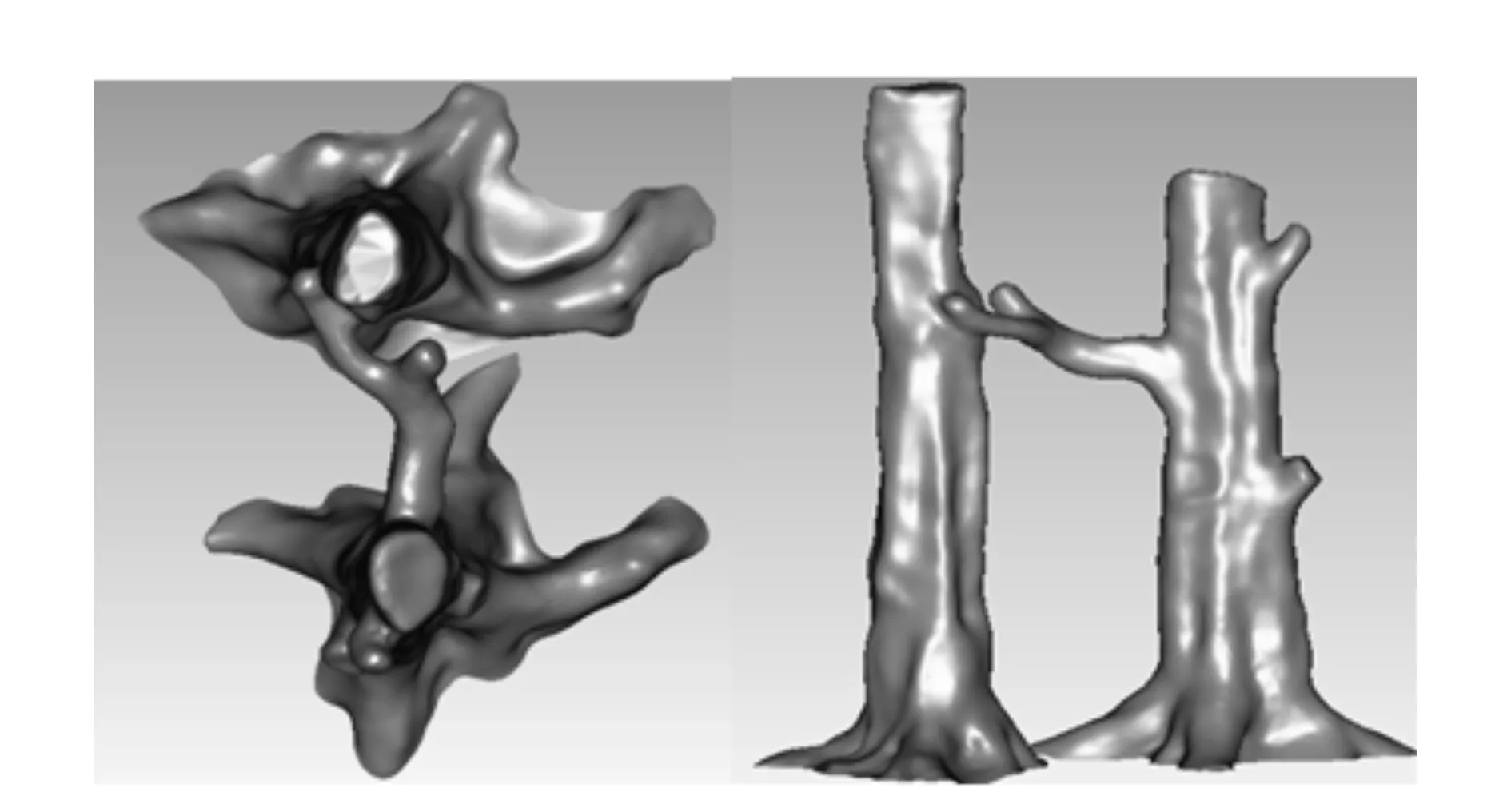
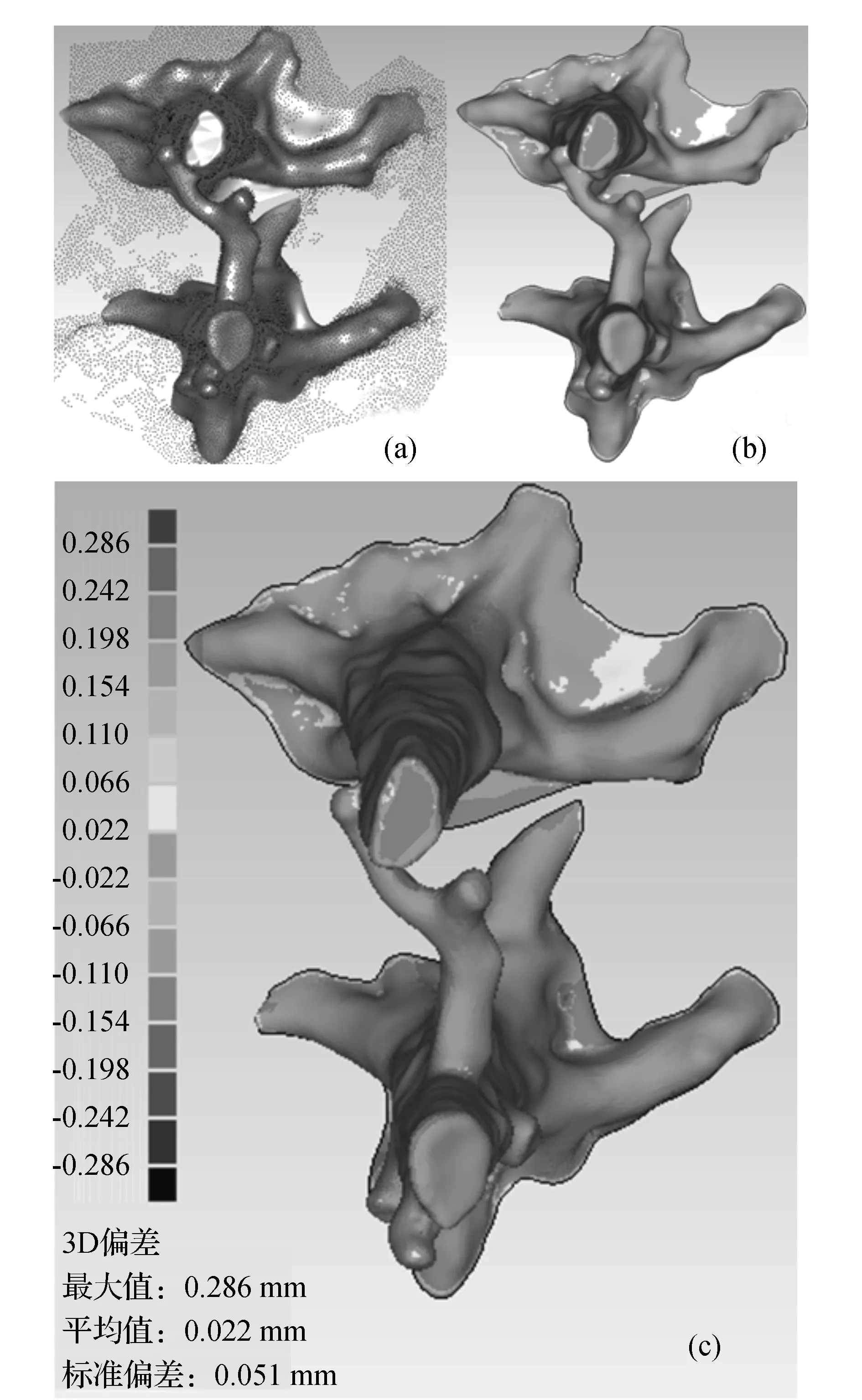
Voronoi图定义:对于平面上离散点集p={pi,0≤i≤n,i∈N},pi是该点集内任意一点,通过pi可以定义一个局部点集Vi,任意一点R∈Vi,有d(R,pi) 图1 Voronoi图 1.2 Delaunay三角剖分定义 Delaunay(Delaunay Triangulation,DT)三角剖分是指点集V的一个三角剖分T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。 1.3 Delaunay三角剖分特性 Delaunay三角剖分组成的三角网格性质如下: 1) 在所有的三角剖分中,Delaunay三角剖分中三角形的最小内角之和是最大的,即最小内角最大性质。 2) 不论从区域何处开始构网,最终都将得到一致的结果,即构网具有唯一性。 3) 任何一个三角形的外接圆都不包含其它的离散数据点集中的点,即空外接圆性质,如图2所示(图中三角形的外接圆边界用虚线表示)。 图2 DT空外接圆性质 以上性质可以确保在Delaunay三角剖分中尽可能不出现过于尖锐的三角形,进而保证构网的三角形最大限度地接近等边或等角三角形。所以,对于平面内的离散点集而言,Delaunay三角剖分是构建TIN技术最为常用的方法。 实现Delaunay三角剖分的算法有多种。由Reifl和Brasse提出以离散点集中的任意一点为起始点,以循环搜索方式查找任意一点一维排序链表中的Dirichlet邻域点法, Lawson提出的逐点插入法实现Delaunay三角剖分算法,其中,Bowyer-Wateson的网格剖分算法是公认的、使用较广泛的算法,其基本思想是:构造一个包含所有散乱点的Delaunay三角形,并将此三角形放入三角形链表中,向初始化的Delaunay三角形中依次插入散乱点集中的点,根据上述内容中的优化方法,完成一个点在Delaunay三角形链表中的插入,依次将所有点插入完毕,然后迭代该过程,直至点集中所有点处理结束。该过程可以用图3表示。本文选取化石林中的化石点云经过三角化后的结果,如图4所示。 图3 Delaunay三角剖分过程 图4 化石Delaunay三角网模型 本文使用Geomagic studio 12所提供的Delaunay三角剖分模块来完成散乱点集的三角剖分以及模型重建。在Geomagic studio12中,实现离散激光点云数据三维表面模型重建过程如下。 3.1 多边形修整 多边形修整阶段主要任务是:1)对点云数据构建Delaunay三角网;2)对构网后的多边形修整,包括基于曲率孔填充、边界修补、光顺边界、特征构建、探测曲线并调整、多边形简化、多边形细化等。图5为多边形修整后的化石,5(a)为修补破孔前的数据,5(b)为修补破孔后数据。 图5 多边形修整前后的化石模型 3.2 曲面编辑 曲面质量的好坏直接影响到三维模型的精度,曲面编辑主要包括特征线提取、特征识别、边界构建、面片组织、面片光顺等。 1)创建曲面片阶段。 2)对创建后的曲面片划分。划分曲面片不能过大,过大导致捕捉点云形状困难,得到曲面质量差。划分曲面片不能过小,过小导致曲面太碎,给后续工作带来一定困难。曲面片划分应遵循以下原则:① 较平滑的部位曲面片少而大。特征多的地方曲面片多而细。② 曲面片的曲率变化尽量保持均匀,这样可以提高创建曲面质量。③ 创建曲面片尽量是四边域曲面。 调整曲面片布局,构建曲面片后,通过对曲面片的控制点增加、减少、改变方向、拖动等方式进行调节,目的是使各曲面片纵横方向有序、方向尽量相同。如图6所示曲面片阶段化石的模型。 3)网格线建立。调整曲面片后,构造“网格线”,对曲面片内的网格线做进一步调整,将其调整到方向一致、均匀的光顺曲面网格为止。曲面片内的网格线越稀疏,曲面数据的精确度相对较低;点云数据文件所占空间较小,数据处理速度较快。与之相反,网格线越密集,精确度越高;数据处理速度较慢。图7所示为网格线阶段化石的模型。 图7 化石网格阶段模型 4)建立曲面模型。基于上述创建的曲面片和网格线,建立无纹理属性的化石表面模型,如图8所示。 图8 无纹理属性化石模型 图9 误差比对模型 3.3 文件输出 为了检查模型是否符合精度标准,需要比较曲面与点云间的误差(3DCompare),如图9所示,其中图9(a)为化石点云数据与化石重建后模型,图9(b) 为曲面与点云间的误差比较过程,图9(c)为曲面与点云间的误差比较结果。 从图9(c)可以得出,曲面和点云间最大偏差为0.268 mm,平均偏差为0.022 mm,标准偏差为0.051 mm,经过查阅文献知其精度符合模型重建要求。 使用三维激光扫描仪获取点云数据进行三维场景重建时,为使模型效果更逼真,可以对模型进行渲染。本实验验证了三维激光扫描仪在三维模型重建领域有一定的实用性。 [1]王晓南,郑顺义.基于激光扫描和高分辨率影像的文物三维重建[J].测绘工程,2009,18(6):53-55. [2]于明旭,纪志浩,黄国斌,等.地面激光扫描和数码相机在化石重建中的应用[J].交通科技与经济,2013,15(4):124-126. [3]胡影峰.逆向工程后处理中基于点线面的曲面重建[J].煤矿机械,2008,29(6):201-202. [4]梁振华,王晨,谢宏全.基于莱卡C10获取校园三维点云数据设计[J].测绘工程,2013,22(1):47-50. [5]权毓舒,何明一.基于三维点云数据的线性八叉树编码压缩算法[J].计算机应用研究,2005(8):70-72. [6]喜文飞,方源敏,李帅,等.一种新的激光点云数据精简方法[J].测绘工程,2012,21(4):38-40. [7] 范剑英.结构光深度图像获取和处理与三维重建研究[D].哈尔滨:哈尔滨理工大学,2012. Research on 3D reconstruction method based on point cloud JI Zhi-hao1,YU Ming-xu2 (1.Xuzhou Sanlian Mapping Co.Ltd.,Xuzhou 221116,China; 2.Jiangsu Vocational College of Architecture,Xuzhou 221116,China) The 3D laser scanning point cloud data is discrete because of the limited resolution and lack of flexibility which lead to be unable to satisfy with the geometric accuracy of the model to the actual scene reconstruction.In order to solve the above problems,the 3D surface model uses Delaunay Triangulation method to construct the grid approximation of an object and the point cloud data of discrete continuous generation of surface model to simulate the scene.The experiments show it is an effective and feasible method to reconstruct the fossil modeling. point cloud; Delaunay triangulation; Voronoi diagram; surface model; three dimensional reconstruction 2014-02-16 纪志浩(1986-),男,助理工程师,研究方向:工程测量. P208 A 1671-4679(2014)03-0007-03 郝丽英]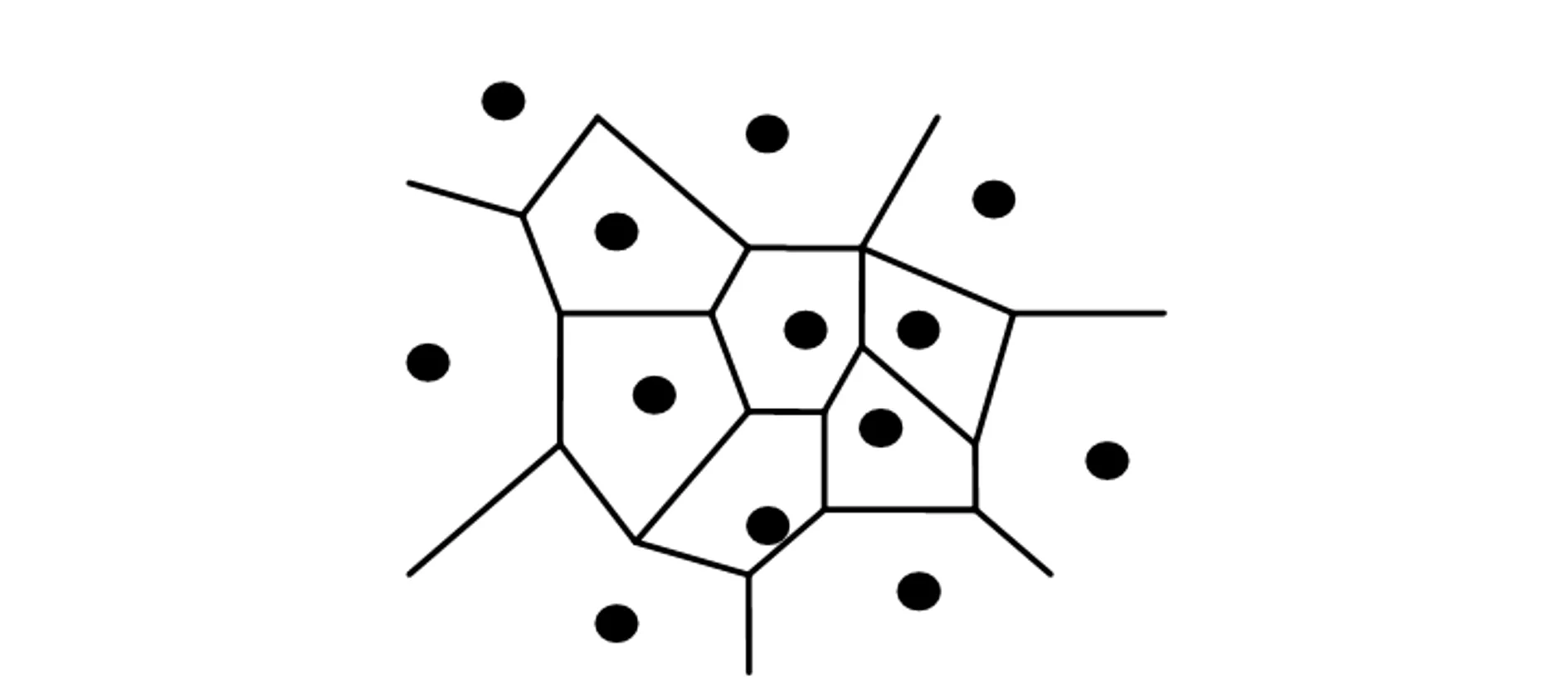
2 构网实现方法
3 模型重建方法

4 结束语
