基于维托假设的连续配筋混凝土路面应力分析与配筋率计算

魏建军，邢姣秀

(黑龙江工程学院 土木与建筑工程学院，黑龙江 哈尔滨 150050)

基于维托假设的连续配筋混凝土路面应力分析与配筋率计算

魏建军，邢姣秀

(黑龙江工程学院 土木与建筑工程学院，黑龙江 哈尔滨 150050)

由于连续配筋混凝土路面板产生干缩变形和温缩变形，导致路面出现横向裂缝，横向裂缝按一定间距分布。利用维托假设，对由温缩和干缩影响下产生裂缝的连续配筋混凝土路面内应力进行分析，重点对横向裂缝间距和最小配筋率的计算公式进行推导。

连续配筋混凝土路面;横向裂缝间距;配筋率;应力

连续配筋混凝土路面由于不设置胀缝和缩缝，需要在其内部纵向设置足够数量的钢筋，用来抵制混凝土路面板纵向收缩产生的开裂。尽管设置钢筋，连续配筋混凝土路面仍会产生一定数量的横向裂缝。根据国内外已有连续配筋混凝土路面的使用情况，横向裂缝间距过小时，混凝土易发生冲断破坏；裂缝间距过大且裂缝的宽度较大时，会降低裂缝处的传荷能力并导致钢筋锈蚀[2-3]。因此，合理地分析配筋后混凝土路面的内应力变化，对连续配筋混凝土路面的纵向钢筋配筋设计，计算裂缝间距和裂缝宽度有很重要的意义。

1 维托假设

维托(Vetter，C.P.)是最早研究连续配筋混凝土路面体积和应变变化的学者之一。维托在不考虑车轮荷载对钢筋应力影响的前提下，提出连续配筋混凝土路面横向裂缝主要是由混凝土材料干燥收缩和温度收缩产生。在分析连续配筋混凝土路面的收缩变形时，维托提出以下三种假设[1]：

1)在路面中段单位长度内，钢筋的变形与混凝土的变形相等；

2)钢筋与混凝土的粘结力与混凝土承受的拉力相等，也与钢筋承受的力的和相等；

3)钢筋受拉的伸长与钢筋受压的缩短量相等。

2 带横向裂缝连续配筋混凝土路面应力分析

假定连续配筋混凝土路面板在干燥收缩和温度收缩作用下，产生横向裂缝将路面分成若干路段，如图1(a)所示。取其中一个路段并设其长度为L，则L即为相邻横向裂缝的间距，如图1(b)所示。

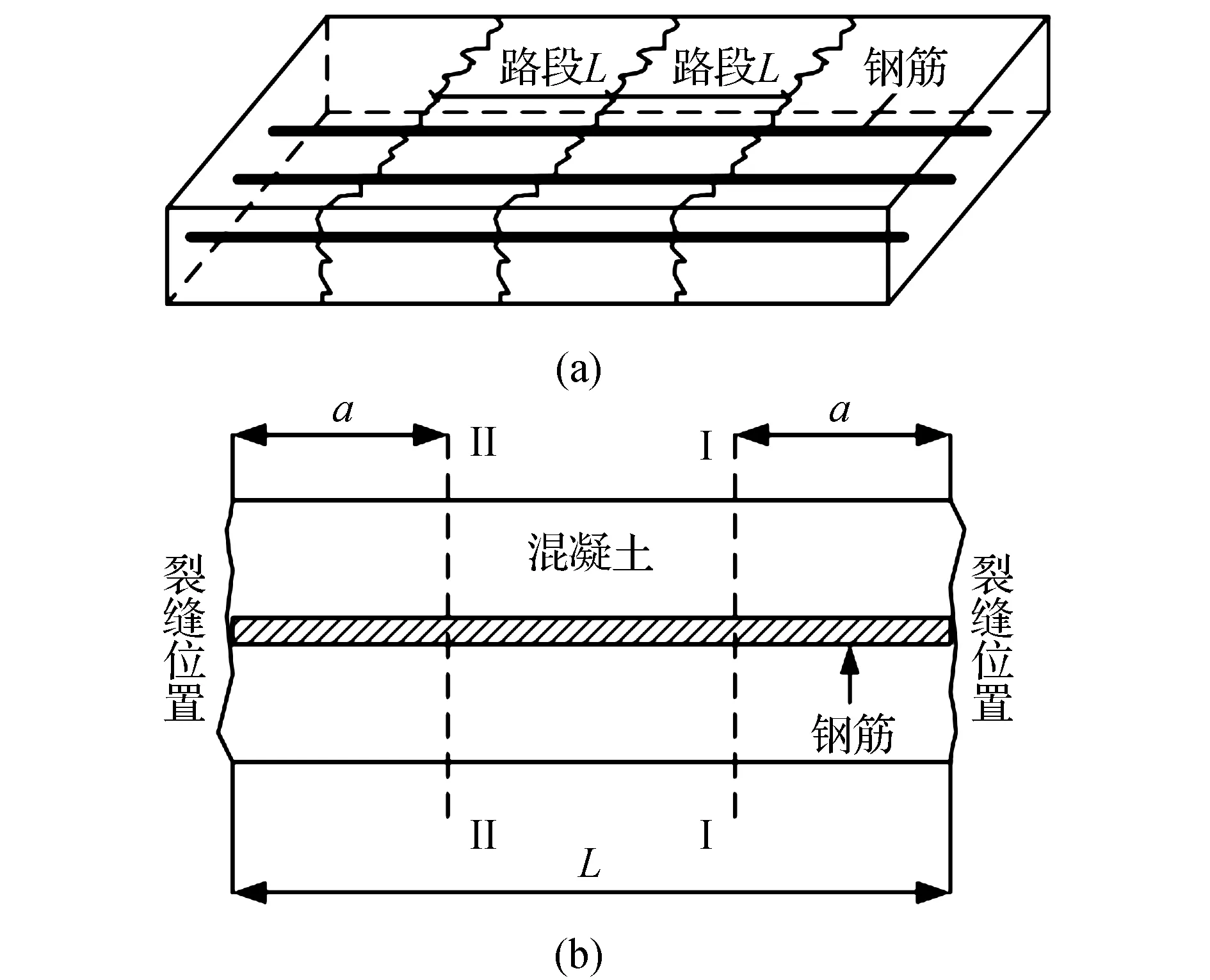
图1 带横向裂缝连续配筋路面路段

路段L在裂缝位置的混凝土不受干缩和温缩应力作用(或约束应力得到释放)，应力为0。随着向路段中心发展，混凝土因干缩和温缩作用受到内部钢筋的约束而产生拉力。拉力大小随混凝土长度增加而增加。假设在距路段L两端裂缝位置长度为a处，混凝土受到拉力与钢筋产生的约束力或钢筋与混凝土之间的粘结力平衡。此时混凝土受到拉力最大，如图2(b)所示。

在裂缝位置处的钢筋，因混凝土断裂所释放应力由其承担而产生拉应力。在长度为a的路段范围内，钢筋从拉力逐渐变化为压力，并与混凝土受到的拉力平衡，如图2(a)所示。

在裂缝位置的钢筋受拉，混凝土不受力。为了实现力的平衡，钢筋与混凝土的粘结应力存在，且为最大值。在路段长度为a处，混凝土受力与钢筋受力达到平衡，此时混凝土与钢筋的粘结力为0。在路段a范围内，混凝土与钢筋之间存在粘结力。粘结应力沿长度呈线性变化，如图2(c)所示。

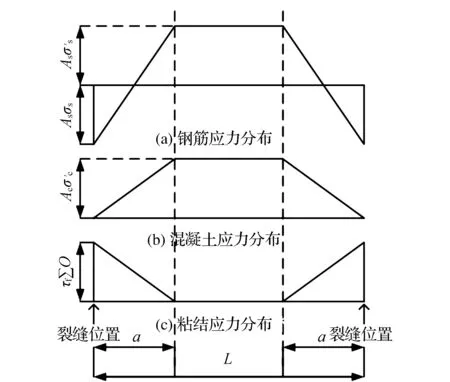
图2 路段中混凝土、钢筋及粘结力应力分布

3 横向裂缝间距计算

根据维托假设(1)，路段L中混凝土受拉产生的变形与钢筋受压的变形相等。式(1)和式(2)分别列出干缩条件和温缩条件下混凝土受拉变形和钢筋受压变形的相等关系。

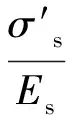
(1)

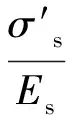
(2)

式中：εsh为混凝土干缩变形，Es为钢筋弹性模量，Ec为混凝土弹性模量，ΔT为混凝土板平均温度的变化(℃)，αc为混凝土与钢筋的相对温度变形系数。

(3)

(4)

取路段L中裂缝端至截面I-I段长度为a的路段为研究对象(见图1)。路段a中的混凝土在I-I断面受到拉力P作用，内部受到钢筋与混凝土粘结力S的作用。路段a中的钢筋在I-I断面受到压力P1的作用，在裂缝一端受到拉力P2的作用。同时还受到混凝土与钢筋粘结力S′的作用。其中S=S′=τfa∑O(见图3)。

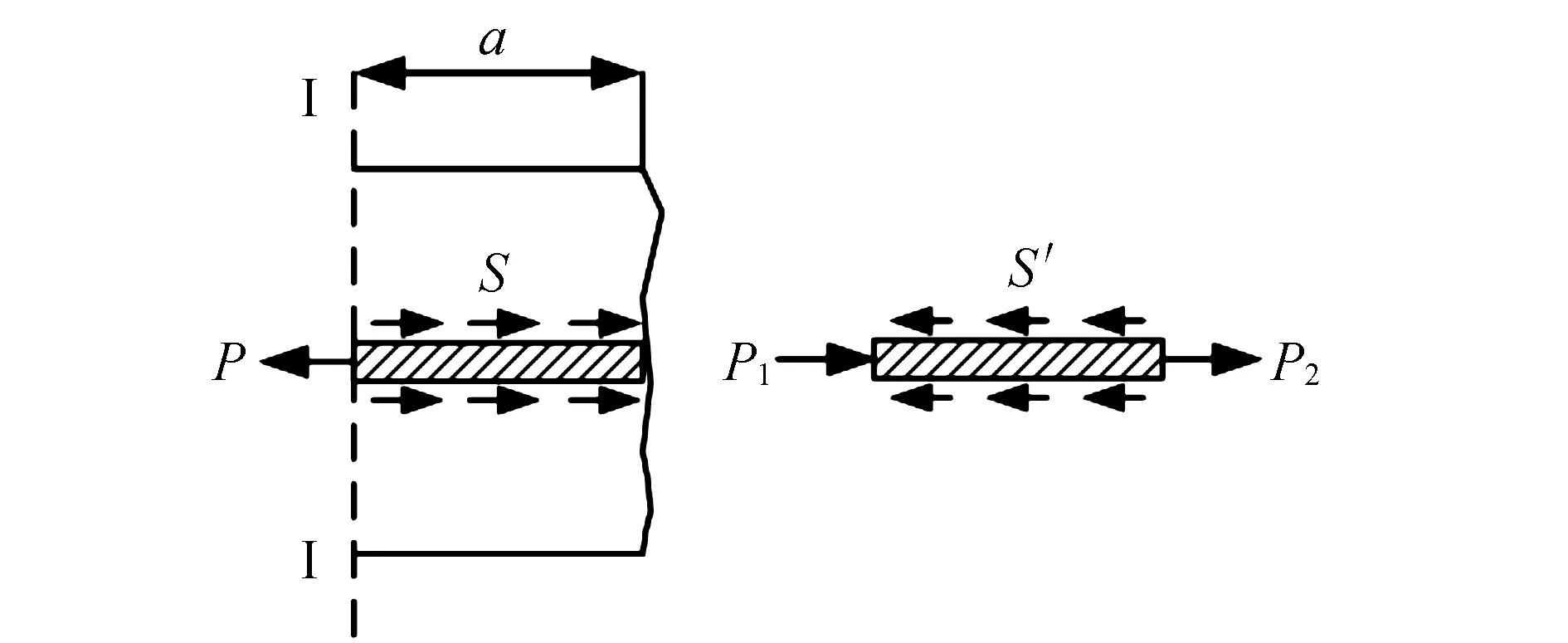
图3 路段a中混凝土与钢筋受力分析

根据维托假设(2)有P=S(混凝土所受拉力与混凝土与钢筋粘结力相等)，即

(5)

P1+P2=S′(钢筋受力与钢筋与混凝土粘结力相等)，即

(6)

由式(5)得

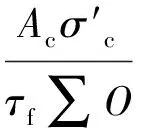
(7)

将式(6)代入式(5)得

(8)

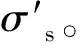
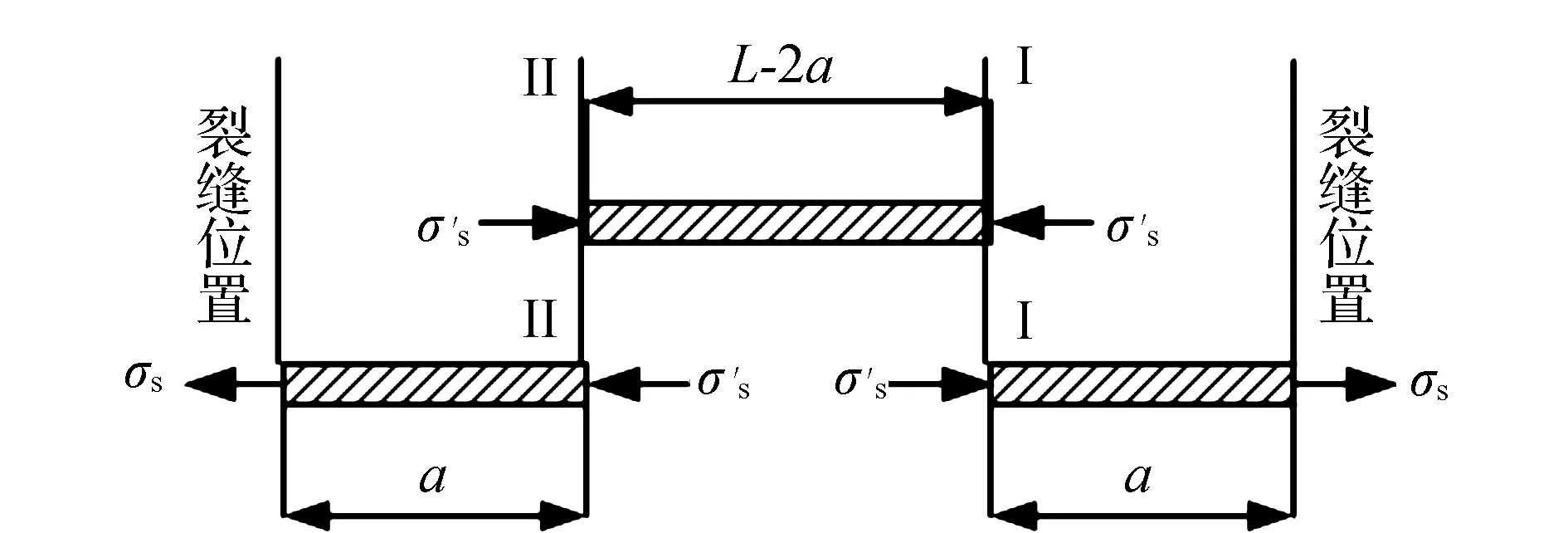
图4 路段L中钢筋受力分析

根据维托假设(3)，则有

(9)

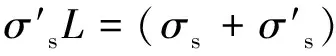
(10)

将式(3)或(4)、(7)和(8)代入式(10),则有

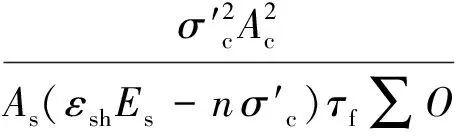
(11)

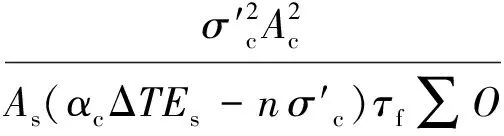
(12)

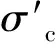
4 最小配筋率的计算

按维托的理论，最小配筋率计算需要满足两个条件:一是保证路段L内不产生新的裂缝；二是保证横向裂缝的宽度稳定，不至于进一步增加。为了保证裂缝宽度的稳定，裂缝处的钢筋不应产生屈服变形，即裂缝位置钢筋受到的拉应力不大于其屈服应力σy。

由钢筋与混凝土的受力平衡条件有

(13)

(σy+εshEs-nσL)As=σLAc，

(14)

(σy+αcΔTEs-nσL)As=σLAc.

(15)

设p为配筋率，则有

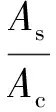
(16)

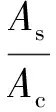
(17)

同时考虑到裂缝位置钢筋受到的拉应力不大于其屈服应力σy的条件，则有

(18)

对于由干燥收缩条件得到的最小配筋率p，必须同时满足式(16)和式(18)的要求。由温度收缩确定的最小配筋率p，必须同时满足式(17)和式(18)的要求。而确定最终最小配筋率时，干燥收缩与温度收缩均要考虑，可根据当地条件、施工条件决定。

5 结束语

连续配筋混凝土路面设计主要包括板厚设计和配筋设计两个内容。配筋设计实际是一个试算过程。需要先假定一个初始配筋率，再通过裂缝间距计算、裂缝宽度计算、钢筋应力计算来验证初始配筋率是否合理。如何提出一个合理的初始配筋率，通常需要根据经验获得。本文通过维托假设推导的连续配筋混凝土路面的最小配筋率计算公式和横向裂缝间距公式，很好地估算出满足混凝土极限拉应力和钢筋屈服条件的最小配筋率和裂缝间距，并可作为配筋设计中初始配筋率的参考值，这对于减少配筋设计中的试算工作有很重要的意义。

[1]邓学均，陈荣生．刚性路面设计[M]．北京：人民交通出版社，2005：426-430.

[2]黄晓明．连续配筋混凝土路面结构内力分析与设计方法研究[R]．南京：东南大学，2011.

[3]罗翥．基于施工过程的端部滑移式连续配筋混凝土路面结构分析[D]．南京：东南大学，2012．

[4]陈志良．连续配筋混凝土路面收缩开裂分析[D]．长沙：长沙交通学院，2003．

[5]杨益兵．混凝土温度干缩裂缝的成因及控制[J]．施工技术，2008(4)：10-12.

[6]张艳聪，田波．隧道内连续配筋混凝土路面早期裂缝发展研究[J]．公路，2012(3)：99-103.

[7]付智，王大鹏．连续配筋混凝土路面文献及路面使用状况调研[R]．北京：交通运输部公路科学研究院，2011．

[8]交通运输部．JTG D40-2011 公路水泥混凝土路面设计规范[S]．北京：人民交通出版社，2003.

[9]张洪亮，左志武．连续配筋混凝土路面[M]．北京：人民交通出版社，2011：38-50.

[10]魏建军，武鹤．公路路基断面形式与路基高度对风吹雪灾害形成的影响分析[J]．黑龙江工程学院学报：自然科学版，2008(2)：4-6.

Stress analysis and reinforcement ratio calculation of continuously reinforced concrete pavement based on Vetter hypothesis

WEI Jian-jun,XING Jiao-xiu

(College of Civil Engineering and Architecture,Heilongjiang Institute of Technology,Harbin 150050,China)

A series of transverse cracks will come into being in continuously reinforced concrete pavement because of temperature changing and shrinkage of the concrete.The transverse cracks distribute in law.Based on the Vetter hypothesis,the stress and strain of continuously reinforced concrete pavement with cracking are analyzed and the formulas of crack spacing and minimum reinforcement ratio are deduced.

continuously reinforced concrete pavement; transverse crack spacing; reinforcement ratio; stress

2014-02-13

黑龙江省普通高等学校青年学术骨干支持计划项目(1153G031)

魏建军(1973-)，男，副教授，研究方向：道路工程.

U416.2

A

1671-4679(2014)03-0001-03

郝丽英]