弱联接玻色爱因斯坦凝聚体中势垒宽度对非线性耦合及其动力学的影响

刘新建，李卫东

(山西大学理论物理研究所，中国 太原 030006)



弱联接玻色爱因斯坦凝聚体中势垒宽度对非线性耦合及其动力学的影响

刘新建，李卫东

(山西大学理论物理研究所，中国 太原 030006)

利用解析与数值方法，对处于对称双势阱中的玻色爱因斯坦凝聚体中，势垒宽度对系统非线性耦合及其动力学的影响进行了研究．研究发现当势垒宽度较大时，系统的线性耦合强度可迅速减小；在势垒宽度大于0.3且非线性强度较大时，线性耦合强度远小于非线性耦合项，此时玻色约瑟夫森结模型的动力学特性由非线性耦合强度来决定．同时对势垒宽度对BEC约瑟夫森振荡的周期和发生宏观量子自俘获时的非线性临界值进行了详细的研究．

对称双方势阱；双模近似； 玻色约瑟夫森结； 宏观量子自俘获

自玻色爱因斯坦凝聚体(BECs)实现以来，理论[1-9]和实验[10-11]都对其进行了广泛的研究．双势阱模型作为一个简单的物理模型，主要研究量子干涉效应和约瑟夫森效应的典型结构．早在1997年Smerzi等人就利用玻色约瑟夫森模型对双势阱中排斥相互作用原子的隧穿动力学进行了研究[1]，并在理论上得出了一种非线性现象：宏观量子自俘获(MQST)[2-4]．十年后在光晶格中人们观察到了约瑟夫森振荡[10]，在双势阱中观察到了约瑟夫森振荡和宏观量子自俘获[11]．这些工作都是基于用一束失谐的激光把一个磁谐振子势从中一分为二，实现双势阱，这样囚禁在其中的BECs就一分为二，适当调节双势阱之间的势垒高度就形成了两团弱耦合BECs．李卫东等人指出在修正的玻色约瑟夫森结模型中不仅存在线性耦合项而且存在非线性耦合项，并且发现在弱耦合，即满足双模近似的条件下，势垒高度和宽度不发生变化的情况下随着非线性增加非线性耦合项将达到甚至超过线性耦合项，从而影响双势阱中BECs的动力学性质[7-8]．我们知道在实验中可以通过调节Feshbach共振改变非线性强度[10-11]．同样可以改变激光脉冲的强度来调节势垒的高度和宽度，从而影响两势阱的耦合强度．本文在对称双方势阱这一模型中，利用文献[8]的方法,研究了势垒宽度对对称双方势阱中BECs非线性耦合强度及其动力学影响．

1 非线性双模近似模型

零温下对称双方势阱中弱相互作用的BECs的波函数满足一维GP方程：

(1)

其中V(x)是双势阱函数形式为：

(2)

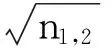
(3)

将双模近似代入GP方程可推导出修正的非线性双模近似动力学方程：

(4)

其中R(..)表示括号中式子的实部．其中κ为线性耦合项，为非线性耦合项．

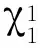
模糊层次分析法FAHP(Fuzzy Analytic Hierarchy Process)是在传统的层次分析法基础上,考虑到人们对复杂事物判断的模糊性,引入模糊一致性矩阵的决策方法。模糊层次分析法很好地解决了AHP判断矩阵的一致性问题。本文在具体采用模糊层次分析法确定各个路由度量权重系数之前,首先作如下假设:

(5)

定义两个势阱中的粒子布局数差z(t)≡n1(t)-n2(t)和相位差φ(t)=θ2(t)-θ1(t)，则非线性双模近似的动力学方程可写为：

(6)

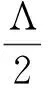
(7)

表1 线性耦合强度与非线性耦合强度随势垒宽度和非线性强度的变化表

取势垒高度V0=200, 通过计算表(1)发现当势垒宽度b≥0.30，即两势阱间的耦合强度较弱，同时非线性参数非线性较强时，会出现κ≪χ 即非线性耦合项占主导作用．此时方程(6)可以忽略κ简化为：

(8)

系统的总哈密顿量为：

(9)

此式比方程(6)更简洁．但此式必须在弱耦合和强非线性同时满足的条件下才能满足．对于双势阱模型所采用的双模近似在耦合强度越弱的情况下，近似程度越高；同时非线性强度可以通过调节Feshbach共振改变．所以上式能很好地描述双模近似模型下强相互作用的量子气体．

2 势垒宽度对动力学的影响

2.1 约瑟夫森振荡

利用(6)式取势垒高度V0=200,势垒宽度分别取b=0.15,0.30，0.45．粒子布局数差初始值z(0)=0.01，初始相位差为φ(0)=0计算出其粒子布局数差随时间变化图像，及其对应的相位差图像．如图1可知，粒子数布局数差平均值为零，所以BECs进行约瑟夫森振荡．势垒宽度增加，势阱间耦合强度减弱，其他条件相同的情况下，势垒宽度越大，双势阱系统中BECs做约瑟夫森振荡的周期越长；相位差的变化周期与粒子数布局差周期规律一致．

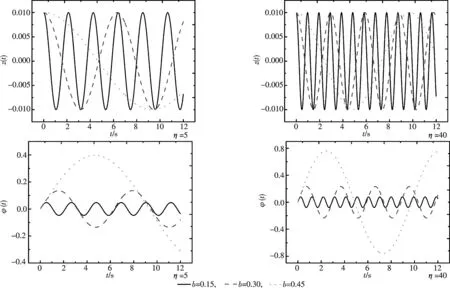
图1 不同势垒宽度和η=5,40时，粒子布局数差和相位差随时间演化Fig.1 The time evolution of particle population imbalance and phase difference for various barrier width and η=5,40

2.2 宏观量子自俘获

同样利用公式(6)取势垒高度V0=200，初始相位差为φ(0)=0，且势垒宽度分别取b=0.15，0.30，0.45．与小幅振荡不同的是这里选取粒子布局数差的初始值z(0)=0.1．计算出其粒子布局数差随时间变化图像及其对应的相位差图像．由图2可以看出不同的势垒宽度在其他条件一致的情况下出现的振荡形式不同；势垒宽度越大的越容易出现粒子数布局数差平均值为非零，即宏观量子自俘获，关于这一点文章后续还有说明．从图2还可以看出当粒子布局数差进入宏观量子自俘获相时，左右势阱中波函数相位差变成了相位的持续增加．

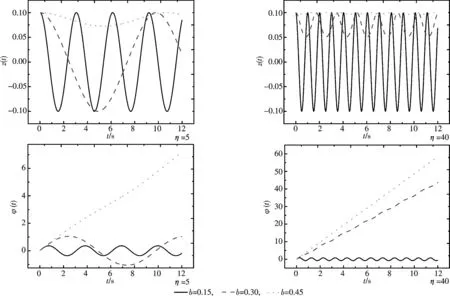
图2 不同势垒宽度和η=5,40时，粒子布局数差和相位差随时间演化Fig.2 The time evolution of particle population imbalance and phase difference for various barrier width and η=5,40

2.3 弱耦合强相互作用下的动力学

当势垒的宽度较宽且非线性较强时，对称双势阱中BECs的隧穿动力学可以用(8)式描述，选取势垒宽度b=0.30，非线性强度为η=80，来比较保留线性耦合项和忽略线性耦合项对其动力学的影响，验证简化式(8)的合理性．从图3可以看出在上述条件下忽略线性耦合项对BECs的动力学影响较小．因此可知(8)式能较好地刻画强相互作用下BECs的动力学行为．

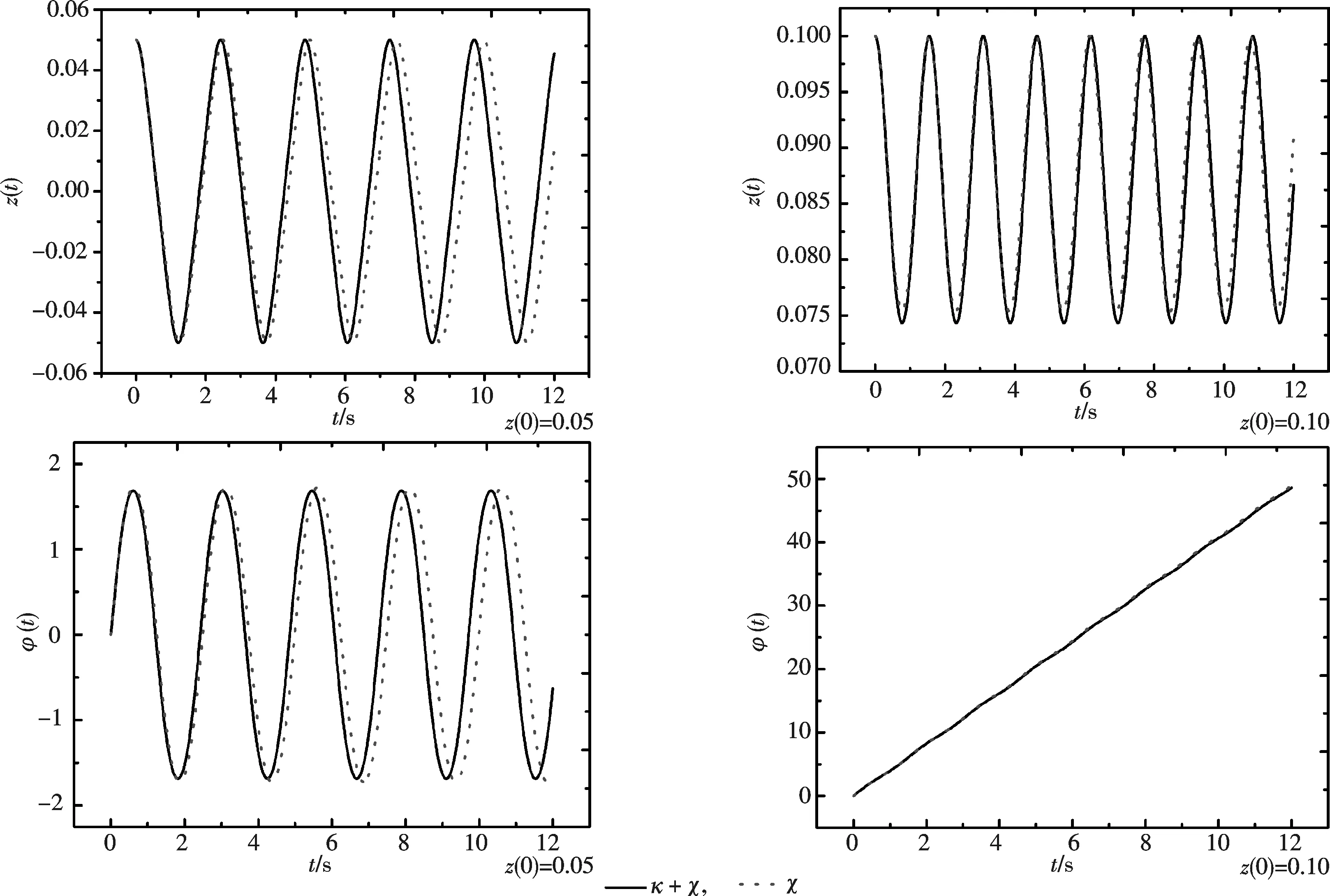
图3 φ(0)=0，z(0)分别为0.05,0.10时保留线性耦合项和忽略线性耦合项时，粒子布局数差和相位差随时间演化对比Fig.3 The contrast time evolution images of particle population imbalance and phase difference between keeping the linear coupling term and ignoring it when φ(0)=0, z(0)=0.05 and 0.10

2.4 势垒宽度对宏观量子自俘获的非线性临界值的影响

宏观量子自俘获现象是玻色约瑟夫森结模型中的一种新奇的量子现象．对于给定的模型中当初始相位差φ(0)=0，对应的初始粒子布局数差临界值为：

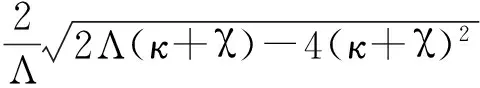
(10)

图4 不同势垒宽度下初始粒子数差临界值随非线性强度变化图像Fig.4 The threshold of initial population imbalance varies with the change of nonlinear intensity under different barrier widths

因此改变势垒宽度和非线性强度都会改变临界值z(0)．由图4可知，随着势垒宽度越大，在相同的粒子数差初始情况下，动力学从约瑟夫森振动向宏观量子自俘获转变的非线性值越小．同时发现势垒较宽的模型出现自俘获的区间较大．

3 结论

在对称双方势阱中，利用修正的约瑟夫森模型，系统地研究了势垒宽度对线性耦合项及其动力学的影响．发现在b≥0.30弱耦合模型，强相互作用下，非线性耦合项将变成主要耦合项，修正的约瑟夫森双模动力学模型(6)式可以简化为(8)式．同时发现在相同非线性强度下，势垒越宽，约瑟夫森振荡的周期越大，宏观量子自俘获的初始临界值越小．通过计算发现在弱耦合强相互作用下简化的约瑟夫森模型能够很好地描述双方势阱中BECs的动力学．

[1] SMERZI A, FANTONI S, GIOVANAZZI S,etal. Quantum coherent atomic tunnneling between two trapped Bose-Einstein condensates[J]. Phys Rev Lett, 1998,79(25):4950-4953.

[2] RAGHAVAN S, SMERZI A, FANTONI S,etal. Transitions in coherent oscillations between two trapped Bose-Einstein condensates[J]. Phys Rev A, 1999,60(3):620-624.

[3] THIAGO F VOSCONDI, FURUYA K. Dynamics of a Bose-Einstein condensate in a symmetric triple-well trap[J]. J Phys A: Math Theor, 2011,44(17):175301-175303.

[4] MAHMUD K W, KUTZ J N, REINHARDT W P. Bose-Einstein condensates in a one-dimensional double square well: Analytical solutions of the nonlinear Schrödinger equation[J]. Phys Rev A, 2002,66(6):063607.

[5] LIN B, FU L B, YANG S P,etal. Josephson oscillation and transition to self-trapping for Bose- Einstein condensates in a triple-well trap[J]. Phys Rev A, 2007,75(3):033601.

[6] CHENG J, JING H, YAN Y J. Spin-mixing dynamics in a spin-1 atomic condensate coupled with a molecular[J]. Phys Rev A, 2008,77(R)(6):061604.

[7] LI W D. Stationary solutions of Gross-Pitaevskii equations in a double square well[J]. Phys Rev A, 2006,74(6):063612.

[8] JIA X Y, LI W D, LIANG J Q. Nonliner correction to the boson Josephson-junction model[J]. Phys Rev A, 2008,78(2):023613.

[9] XIE Q T, HAI W H. Coherent control of self-trapping of two weakly coupled Bose-Einstein condensates[J]. Phys Rev A, 2007,75(1):015603.

[10] MAHMUD K W, PENG H, REINHARDT W P. Quantum phase-space picture of Bose-Einstein condensates in a double well[J]. Phys Rev A, 2005,71(2):023615.

[11] ALBIEZ M, GATI R, FOLLING J,etal. Direct observation of tunneling and nonlinear self-trapping in a single bosonic josephson junction[J]. Phys Rev Lett, 2005,95(1):010402.

(编辑 陈笑梅)

The Effect of the Barrier Width on the Nonlinear Coupling and Dynamics of Weakly Coupling Bose-Einstein Condensates

LIUXin-jian*,LIWei-dong

(Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China)

By using analytical and numerical methods, the effects of barrier width on the strength of nonlinear coupling and the dynamics of Bose-Einstein Condensates with symmetrical double square well were investigated. The results show that the linear coupling could be very small once the barrier width is large. When the width is larger than 0.3 and nonlinear parameters larger, the linear coupling can be safely neglected. In this case, the dynamics character of Bose-Jsoephson model is determined only by nonlinear coupling strength. Furthermore, the effects of this width on the period of the nonlinear Josephson oscillation and the nonlinear threshold value in macroscopic quantum self-trapping were presented in details.

symmetric double square well potential; two mode approximation; Bose-Josephson junction; macroscopic quantum self-trapping

2014-02-24

国家自然科学基金资助项目(11374197；11074155；10934004)

O469

A

1000-2537(2014)03-0053-05

*通讯作者,E-mail：15364839097@163.com