高中数学变式教学的探索

王才正

(浙江省温岭市松门中学，浙江 温岭 317511)

教育的目的是促进学生的发展，而教学方法的合理选择是实现这个目的根本保障。变式教学是数学学科在不同课型中选择较多的一种方式，其目的是提升学生的思维品质和能力，不同的教育理念和方式，会有不同的结果。为此，笔者从自己的教学感悟到，要让自己的“变式教学”合理、科学，适合学生实际，我们必须研究学生，研究变式教学的特点，从课堂教学实际意义和价值去探索变式教学的内在规律，让“变式教学”成为学科兴趣的培育沃土，问题解决的策略台阶；让“变式教学”为拓展学生的思维视野的广阔天地，提升学生的理性思辨力的有效手段。本文以自己对圆锥曲线的教学体验，探索对变式教学的一些认识，原与同行们共勉。

1 调起点，以本为“本”自然做实“求变”台阶

很多高三教师都深有体会：“以本为‘本’”，才是我们最好的教育策略。在教学中，若注重对课本习题进行变式训练，给学生一定的台阶，让学生变，让学生解，让学生用，不但可以提高学生学习的积极性、主动性，加深学生对基础知识的理解和掌握，而且还可以使学生举一反三,提高学生对数学知识的应用能力，从而培养学生的创新、探究能力， 提高学生的数学素质，进而快乐地学习数学。现在的教学资源很丰富，随处可得，该用哪些资料，有时教师和学生很难定夺，特别是不时会忘记了最正宗的还是课本。根据几年的高中教学经验认为教师所选用的习题应“源于课本”然后对它进行变式，使它“高于课本”，变式要以“考纲为纲”，以“学生为本”。

以在选修2-1的第二章节上完后，章节小结复习前的一节准备性习题课为案例进行论述。

例1：(课本选修2-1，P73习题2.4．由学生独立完成，3分钟)直线y=x-2与抛物线y2=2x相交与两点，求证：OA⊥OB。

编者意图：作为解析几何的精髓——坐标法，由“设点”开始，将几何问题坐标化，通过合理转化问题形式及相关代数运算，研究解决几何问题。无疑这一核心知识的要点：熟悉模块的问题模型(交点模型)，认知“问题解决”的思维策略(数形结合)，感悟“合情推理”之上策。本题很好地诠释了这一命题原则。

课堂上，在学生完成课本习题的基础上，让他们总结了解决方法特点与关键之处(韦达定理运用)，并给了下列“变式”以进一步体会、感悟这一思想方法和精髓。

变式1： 已知抛物线x2=2py(p>0)，直线l过点M(0，2p)，且与抛物线相交于A(x1,y1)和B(x2,y2)两点。求证：OA⊥OB。巡视了几分钟后，让学生回答独立完成情况。

生1： 根据“交点模型”的需要，我们先设了AB直线方程为y=kx+2p，…(即解法1)。

解法1 设AB直线方程为y=kx+2p，与x2=2py(p>0)联立后，消去y，得：x2-2pkx-4p2=0，则x1x2=-4p2，

x1+x2=2pk……①

y1y2=(kx1+2p)(kx2+2p)

=k2x1x2+2pk(x1+x2)+4p2……②

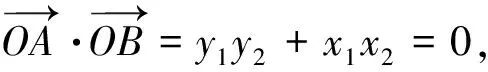
生2： 发现A、M、B三点共线，由向量共线的坐标可得出字母关系，…(即解法2)。

则-x1(y2-2p)-x2(2p-y1)=0，利用点A、B在y=x2/2p，消去y1、y2.得：x1x2=-4p2,y1y2=4p2.以下步骤解法1。

师：同学们解答的很好，在抛物线问题中点坐标的单参设法也往往会简化运算，如果设A(2px1,2py1)，B(2px2,2py2)运算更为简便，大家下去后，可再试试！

师：大家通过同一问题中的三种不同“设点”处理，发现在以“抛物线”为曲线背景的问题中，每种设法各有优缺点，合理选择对运算量会产生直接的影响，也可以设直线方程用韦达定理。当然，一个数学高手不但会解题，还要会想题、变题．谁能说此题与原题的区别在哪？

生4：条件的字母化，还有直线方程不知，交点模型中方程是必须的。

生5：不一定要直线AB的方程，如“生2”解法，用向量的共线知识也行。

生6：我感觉用什么方法不是问题，关键是要想到将“OA⊥OB”，如何转化成“坐标化”关系：xx2+y1y2=0，再根据此式特点，结合问题条件特点，进一步寻求关系。

师：有点高手交流“过招”的意思，那么，谁能把这问题“变一变”，让大家看看，我们会怎么想？

生6：这方便呀，把条件与结论交换一下，就行了，即：

变式2： 已知抛物线:x2=2py(p>0)上A、B，是异于原点O的两点，满足OA⊥OB，求证：直线AB过定点，并求此定点坐标。

师：这是原命题的什么命题，正确吗？请大家试试，看能否完成对其正确性的证明？

生2：设AB直线方程为y=kx+b与x2=2py(p>0)联立消y利用韦达定理得结论。

∴x1x2=-2kb=-4p2，∴b=2p。当k不存在时，易得b=2p，∴直线ABAB过定点(0,2p)。

点评：抛物线问题中“设点”方式有如此之变，且对计算量直接相关，那么，椭圆，双曲线问题中行吗？学生常常会这样想，特别是理科生，一是所遇椭圆为背景的问题多，二是自信自己的计算能力，只有经历了，明确了因这里的横坐标和纵坐标是可以不“开方”，就能表示的，但在椭圆和双曲线就无法，只能设直线方程，用“参数”来表示了。数学学习离不开解题，于是，解题教学成了数学教学中的一种极为重要的教学模式。如何驾驭解题教学的课堂，不仅直接反映教师的专业水平，也直接影响到学生的数学学习兴趣与水平。因为我们不是为了解题而学习数学，我们是通过解题而获得思维的某种方式而提高解决问题的能力。于是，变式训练——围绕数学课本习题的合理组织、运用与思维方法的不断深化来展开，努力营造一种宽松、民主，积极向上的课堂氛围，并引领学生学会变式地处理问题的方式，获得勇于探索、创新的良好思维习惯。

2 重自悟，围绕“兴趣、解决策略”提升“求变”意识

美国数学教育家波利亚曾形象的指出：“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在四周找一找，很可能四周就有好几个。”

我们再看例1(简称原题)，原题→变1，它是由数字向字母变化，使问题“一般化”了，但解决策略未变，手法未变；变1→变2时，问题的结构反转了一次，它是一种“命题结构”的自然变化，也就是说问题的层次未有改观。为此，为了激发学生对数学的兴趣，体会问题的解决策略，我对题中两个条件：①过原点，②OA⊥OB，向学生提出质疑——对于题目中的条件，能否“放宽”一点，你认为改变后，会变成新的问题吗？有何发现呢？

于是，学生根据自己的学习过程的“经验”，稍稍地“移植”到了这里，作有一次有益的尝试：(巡视中，我与学生交流)

生：若将原点O变成抛物线上任意的一个定点M(x0,y0), 直线AB还过定点吗?

生：能将OA⊥OB，改成斜率的其它关系呢？∵垂直，就是斜率之积为-1呀？

师：把你们的变化问题给我看看，显然，这是基于上述质疑所生之变式：

变式3：已知抛物线C：x2=2py(p>0)过点M(x0,y0)，作MA⊥MB，A，B在抛物线C上，求证：直线AB过定点，并求定点坐标。

变式4：已知抛物线:x2=2py(p>0)，过点M(x0,y0)，作直线MA，MB，交抛物线于A，B，若MA，MB的斜率存在，且互为相反数。求证：直线AB的斜率为定值。

点评：课上也许没有时间来具体求解，但这种对数学的自我领悟和兴趣，是无法用其它来代替的，特别是问题的探究能力，即景生成效果，是无法用其它形式所代替的。

师：(我临时打开了投影仪，将“变式3、4”展示在屏幕)，时间有限，先请大家集中屏幕上，变得如何？“变式3”将原题中的“特殊点”改为“一般点”，这“由特殊到一般”的思考问题的方法，我们经常遇见，在数学问题的认识中，更是“比比皆是”；“变式4”将原题中的“垂直”改为“斜率互为相反数”。变的好，高手，实在是高，真的有点高手的水平！

生：(众笑)高，是高，但这类“定点、定值”问题，咱——

师：怎么，没有信心吗？让我亲自解一个(他们毕竟才高二)，想考考我是吧！好了，咱来解一个，你们得解一个——请注意，我是怎么想到的？

点评：兴趣和信心，这是数学学习中，影响学生学好数学的两个非常重要的“非智力”因素，新课程的“三维目标”之一，常常会被教师的“讲题目”所“丢失”了，而这一教学片断，无疑对“情感目标”的落实，完全融于无形之中。毫无疑问，在这“情感目标”营造的氛围之下，学生注意力的高度集中，思维的极度兴奋，教师的激情也完全被点燃，课堂“出彩”也就自然而然了。(以下是学生给出的变式5，及解法，以此佐证这一说法！)

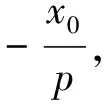
∴直线PA，PB的斜率互为相反数。

点评：圆锥曲线问题的运算量大，综合性强，方法灵活多样，学生对解圆锥曲线题目都有一种害怕和厌恶，教师如何通过课堂教学提高学生的兴趣，信心尤为重要。上面三个变式从特殊到一般，类比问题和逆命题的考察等，以围绕“兴趣、解决策略”提升“求变”意识，对提高学生学习的积极性、主动性，加深学生对基础知识的理解和掌握，而且还可以使学生举一反三，提高学生对数学知识的应用能力，培养学生学习圆锥曲线的兴趣、热情、信心。

3 讲实效，围绕核心知识、方法凸显“求变”原理

从课本出发，在核心知识、方法中畅游，作为学习的引路人，要懂得——教师需题海中“畅游”，而学生应该在题海“拾贝”——的道理，教学中，教师的职能，是最大限度地让学生学会在核心知识与方法的支撑下，真正地体会解决问题的策略与变化本质，不可以让学生沉湎于“题海”之中。为此作为本题的“横向变式”，给学生提出了一个思考问题，并给出了相应的“变式6”：

思考：将上述抛物中成立的问题，能推广到椭圆中成立吗？

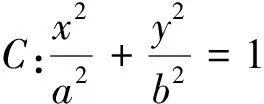
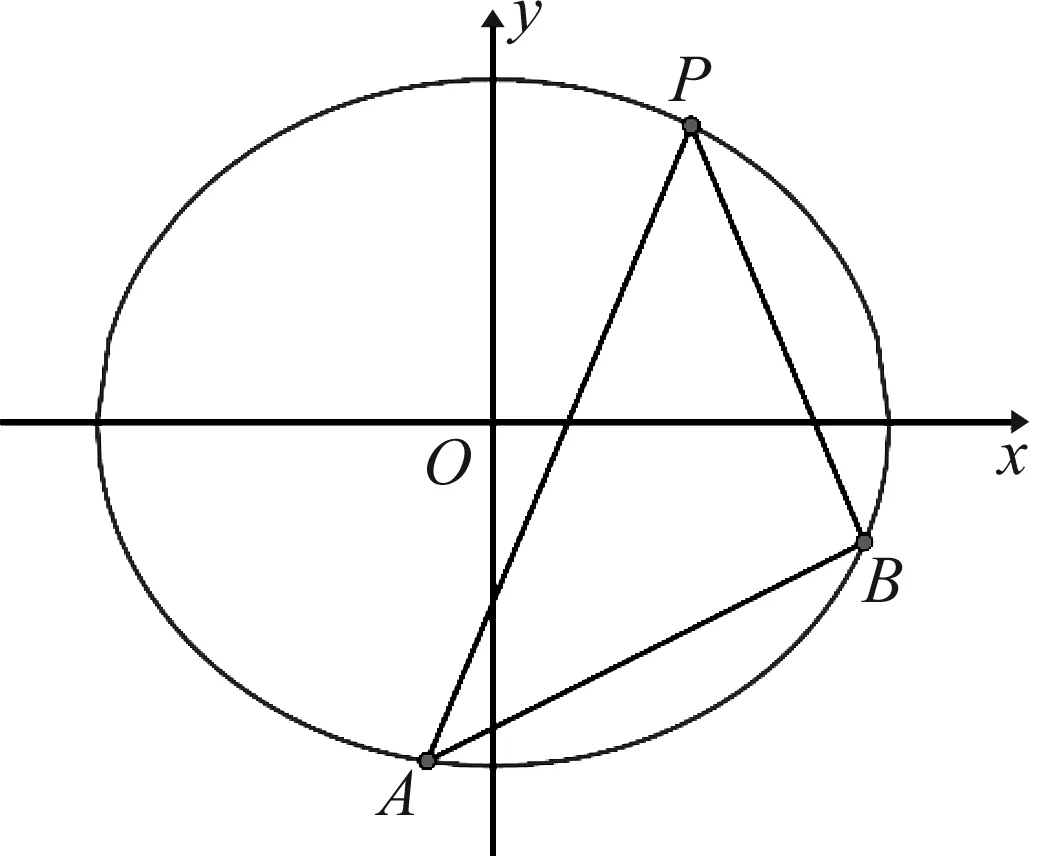
试题分析设问：①本问题的已知条件、结论是什么？②证明“充要条件”要证什么命题，你有这方面的经验吗？③本问题与我们常见的“交点模型”对比，我们现在急需什么？④能出一个图帮助思考一下吗？

解：(必要性)

设直线PA的方程为：y-y0=k(x-x0)，

则直线PB的方程为：(由学生回答)

(此处质疑：椭圆方程为何这样？)

(b2+a2k2)x2+2ka2(y0-kx0)x+a2(y0-kx0)-a2b2=0

(此处质疑：往下应该做咱？由学生寅出)

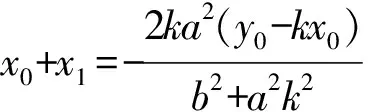
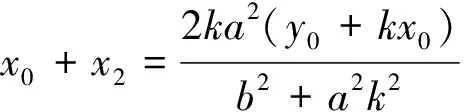
(此处“同理”，具体怎么得来？)

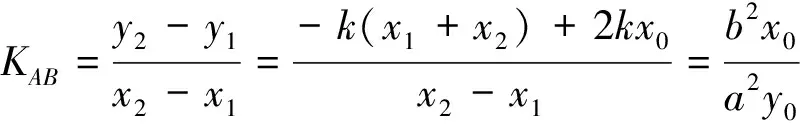
同理可得(充分性)

点评：圆锥曲线的本质是用代数方法解决几何问题，代数方法就是利用方程和函数、不等式等，在解题中，通法是“交点模型”，其“程序化”程度较高→联立方程、消元、设点(设而不求)、“Δ”与“韦达定理”，至此，再根据“设问”变化。比如在这道题目中的运算量是比较大的，但灵活的应用韦达定理就可以避免去解点的坐标，这对简化运算，提高计算的正确率是很有帮助的。这种“程序化”较高的模型化思维方式，对学生来说，需要知道其问题于其中所凸显的“求变”原理。其实，高中数学问题中，这种认知模型是比较多的——利用函数、不等式可以解决范围；利用导数可以解决抛物线的切线；利用导数研究函数性质应用类的等等，所以在解决圆锥曲线问题中要数形结合，用好代数工具。通过变式教学，问题探究，让学生掌握解决圆锥曲线的通法和处理运算过程的一些基本运算、推理能力，把学生学习的兴趣激发出来，充分发挥学生自身的主观能动性，强化创新意识，在探索中求进步，在学习中找经验，在学习中找快乐．学生也就有兴趣有信心去算下去，这样对培养学生学习的兴趣、热情、信心和培养学生的计算能力和意志力是很有帮助的。

4 善拓展，围绕“思维方式与能力”回归“求变”真谛

在高考的圆锥曲线题目中对学生的思维和综合的分析能力，解决能力的要求都比较高，但能力不可能靠教师的讲解来“输入”提高。“问题的演变”与“解后的反思”，是最为常规和理想的能力提速器。为此，我明确地告诉学生，下面问题，是2010年清华自主招生的一道难题．如果知道上面规律，那么这道难题，也就不那么难了！

问题：(2010年清华自主)

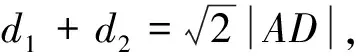
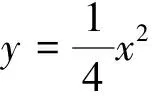
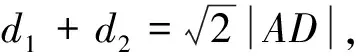
∠DAE=∠DAF=45°，所以ΔABC为直角三角形。

点评：学生对重要考试的考题都有一种好奇和向往，而在高考的圆锥曲线题目中对学生的思维和能力的要求是非常高的，这就要求学生在掌握通法的基础上学会对问题解决策略的分析，反思和总结。

总之，圆锥曲线是高中教学很重要的一部分内容，计算量大，蕴藏的数学思想方法多，一直是学生较难掌握的部分，学生学习积极性或者不高，或者积极性有但效率不高。通过课堂上的变式教学是提高学生的“类比、移植”能力，提高课堂效率和学生学习的积极性的一种非常有效的途径。在数学习题变式教学中，习题的变式要紧扣《考试说明》，要以考纲为“纲”进行“变”；不要“变”出一些偏离考纲的“繁、难、杂”题目来浪费学生的宝贵的学习时间，挫伤学生学习数学的兴趣。多研究如何从“课本习题”出发，课本是专家们的“心血”，往往隐藏着很多“道理”，需要我们去领会和研究、挖掘它。变式教学虽然有点儿“传统”，但我们只要立足于学生的“学”，实践证明它仍然是一种能适应新课程改革的“优化”学生学习方式的教学模式，特别是让学生参与“变式”之中，同样有利于学生自然地接受知识吸收消化知识，有利于学生思维和解决问题能力的提高，关注了学生个性的发展，这符合新课程理念中提出的关注学生个体的发展理念。更重要的是通过变式教学，培养学生敢于思考，敢于联想，敢于怀疑的品质，培养学生自主探究能力与创新精神，学生在无穷的变化中领略数学的魅力，在“奇妙”的演变中体会数学的快乐。