基于量子粒子群算法的结构模态参数识别
2014-09-07刘大山
常 军,刘大山
(苏州科技学院 土木工程学院,江苏 苏州 215011)
结构模态参数识别作为了解结构健康状况的必要前提,其研究备受关注。结构模态参数识别方法主要有频域法、时域法两类。频域法为利用输入输出所得频响函数识别结构模态参数,为传统的识别方法,常见有峰值法、频域分解法等。时域法为利用系统响应的时间历程曲线识别结构模态参数,其原始数据为时间历程,如自由响应、脉冲响应。常见时间序列法、随机减量法、随机子空间方等。两类方法结合使用是目前模态参数识别的一大热点,即时频域方法,常见有小波分析法、Hilbert-Huang变换法等。
量子粒子群算法(QPSO)为在粒子群(PSO)算法基础上发展的基于群体智能理论的优化算法,因其具有所需参数少、编程简单、易收敛及收敛速度快等优势备受关注。QPSO算法应用范围较广,如天线设计、生物医药、通讯网络、分类与聚集、组合优化、自动控制、电力系统设计、电磁场设计、滤波器设计、金融风险预测、投资决策、人脸检测与识别、神经网络与车间调度等[3-15];但在土木工程领域的应用较少见[9]。本文通过将结构模态参数识别问题转化为优化问题,采用QPSO算法进行模态参数识别。
1 粒子群算法
粒子群算法(Particle Swarm Optimization, PSO)由Eberhart等[1-2]提出。与其它进化算法类似,该算法具有进化及群体智能特点,可模拟鸟群飞行觅食行为,通过鸟间协作、竞争达到群体智能目的。在PSO算法中,每个候选解成为一个“粒子”,若干候选解构成鸟群体。每个粒子无重量、体积,通过目标函数确定其适应值,并在解空间中运动,由速度决定其运动方向、距离,粒子通过追随自身的个体最好位置与群体全局最好位置动态调整自己的位置及信息。该算法中,粒子运动状态由位置、速度描述,随时间的演化,粒子运动轨迹为既定的,而粒子速度受到一定限制,使粒子的搜索空间为有限并逐渐减小的区域,不能覆盖整个可行空间,从而导致PSO算法不能保证全局收敛。此结论已被证明[3]。此为PSO算法的致命缺陷。
2 量子粒子群优化算法
孙俊等[6-7]由量子力学角度提出新的粒子群算法模型。认为粒子具有量子行为,并据该模型提出量子粒子群算法(Quantum-behaved Particle Swarm Optimization, QPSO)。实际应用表明,该算法具有更好的全局收敛性与不易陷入局部最优的特性。

(1)
式中:u~U(0,1);L为δ势阱特征长度,随时间变化。
经推导,粒子更新方程[5-7]为
(2)
pid=φpij+(1-φ)Gj
(3)
(4)
式中:m为粒子数;n为维数;φ~U(0,1);pij为由个体经验知识确定的最优值;Gj为由群体知识确定的群体最优值;α为收缩扩张系数,即QPSO算法除群体规模及迭代次数外的唯一控制参数,计算式[5-7]为
(5)
式中:α1,α2分别为α的初始值、终值;t为迭代次数;Imax为允许最大迭代次数。
QPSO算法过程如下:
(1)t=0时,初始化每个粒子位置为Xi(0),个体最优位置为Pi(0)=Xi(0);
(2) 计算粒子群平均最好位置pm;
(3) 计算粒子i当前位置Xi(t)的适应值,若f[Xi(t)] (4) 对粒子i,将Pi(t)适应值与全局最优位置G(t-1)的使用对比,若f[Pi(t)] (5) 计算随机点位置; (6) 计算粒子的新位置; (7) 若未达终止条件返回(2),否则结束。 多自由度粘性阻尼线性系统传递函数[16]为 (6) 用有理分式多项式可表示[16]为 (7) 式中:N为模态阶数;akak,bk(k=0,1,2,…2N)为待定系数,均为有理数。 令jω=s,b2N=1,得频响函数[16]为 (8) (9) 两边同乘D(jω),得: (10) 式中:ei为加权误差函数: (11) 所有L个对应频率点ω=ωi(i=1,2,…L)的加权误差函数构成误差函数向量为 {e}=[e1e2e3…eL]T (12) 式中:T表示转置。 将上式表示为矩阵: {e}L×1=[P]L×(2L+1){a}(2L+1)×1-[T]L×2N{b}2N×1-{ω}L×1 (13) 式中: [P]L×(2L+1)= (14) [T]L×2N= (15) {a}(2N+1)×1=[a0a1…a2N]T (16) {b}2N×1=[b0b1…b2N-1]T (17) (18) 定义目标函数为 E={e}H{e} (19) 式中:角标H表示共轭转值。 目标函数为 (20) 用QPSO算法可识别出待定系ak(k=0,1,…2N)及bk(k=0,1,…2N-1)。 令D(s)=b0+b1s+…+b2N-1s2N-1+s2N=0,求解得N对共轭复根为 (21) 进而得: (22) 研究表明,某点振型分量与该点留数成正比。设q点激励,p点相应传递函数Hpq(s)第r阶留数[16]为 (23) 通过对一系列响应测点所得留数进行处理,并归一化,得振型向量[16]为 {φr}=[Ar1qAr2q…ArMq]T/Armq (24) 式中:Arpq为q点处激励p点处响应留数;Armq为q点激励时各测点处最大留数。 6层剪切型框架结构模型见图1,结构特性见表1。 表1 六层框架模型结构特性 图1 六层框架模型 激励信号采用正弦扫频信号,频率范围设为0.5~20 Hz,施加于框架各层。测出各层相应,求出各层频响函数。分别采用QPSO算法、PSO算法及峰值法进行结构模态参数识别,结果见表2。在识别过程中PSO、QPSO算法的离子数目均取30,迭代次数3 000。为研究QPSO算法的抗噪性,对识别结果分别加入5%、10%、20%、30%的噪声(噪声最大幅值与响应信号最大幅值之比),用QPSO算法进行识别,结果见表3。QPSO、PSO算法识别前六阶阵型见图2~图7。 表2、表3中MAC为模态判定准则[16]: (25) 判定两向量是否具有相同的相关因子,若MAC接近1,说明两向量相同,接近于0,则不同。 表2 采用不同方法所得计算结果 表3 采用QPSO算法识别不同噪声水平下计算结果 图2 第一阶模态振型 图5 第四阶模态振型 由表2、图2~图7结果看出,本文QPSO算法能较精确识别出模态参数,且较PSO算法、峰值法精度高。由表3看出,QPSO算法能精确识别出噪声影响下的输出信号模态参数,表明该方法抗噪性较强。 通过将由结构输出输入计算所得实测频响函数与理论频响函数差值作为优化问题目标函数,采用量子粒子群算法寻求理论频响函数公式中所含模态参数而使目标值最小化。将模态参数识别问题转化为优化问题。通过采用QPSO算法、PSO算法及峰值法对六层框架结构进行模态参数识别,结论如下: (1) QPSO算法能有效识别结构模态参数,识别精度高于PSO算法、峰值算法; (2) 采用QPSO算法对不同噪声水平影响下的结构输出信号分析表明,QPSO算法能精确识别结构的模态参数,即QPSO算法抗噪性较强; (3) 基于量子粒子群算法对结构健康监测及结构状态评估发展有一定促进作用。 [1] Eberhart R C, Kennedy J.Particle swarm optimization[J].IEEE International Conference on Neural Networks, 1995, 2:1942-1948. [2] Eberhart R C, Shi Y H.Particle swarm optimization developments, application and resources[J].Congress on Evolutionary Computation,2001, 1(2):81-86. [3] Van den Bergh F, Engelbrecht A P.A new locally convergent particle swarm optimizer[J].Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, 2002, 3(7):94-99. [4] Leandro dos.Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems[J].Expert Systems with Application, 2010, 137(6):1676-1689. [5] Liu Jing, Xu Wen-bo, Sun Jun.Quantum-behaved particle swarm optimization with mutation operator[C].Proceedings of 17th International Conference on Tools with Artificial Intelligence, Hongkang(China), 2005: 3078-3093. [6] Sun Jun, Xu Wen-bo, Feng Bin.Adaptive parameter control for quantum-behaved particle swarm optimization on individual level[J].Proceedings of IEEE International Conference on System, 2005,4:3049-3054. [7] Sun Jun, Xu Wen-bo,Fang Wei.Quantum-behaved particle swarm optimization with a hybrid probability distribution[J].Pricai Trends in Artificial Intelligence, 2006,4099:737-746. [8] 公茂盛,谢礼立,欧进萍.结构振动台模型模态参数识别新方法研究[J].振动工程学报,2010,23(2): 230-236. GONG Mao-sheng, XIE Li-li, OU Jin-ping.A method for modal parameter identification of structural shaking table model[J].Journal of Vibration Engineering, 2010, 23(2): 230-236. [9] 胡峰,吴波,胡友民,等.利用粒子群优化算法实现阻尼比和频率的精确识别[J].振动与冲击,2009,28(7):8-11. HU Feng, WU Bo, HU You-min, et al.Exact evaluation of damping frequency based on particle optimization algorithm[J].Journal of Vibration and Shock, 2009,28(7): 8-11. [10] 黄宇,韩璞,刘长良,等.改进量子粒子群算法及其在系统辨识中的应用[J].中国电机工程学报,2011,31(20): 114-122. HUANG Yu, HAN Pu, LIU Chang-liang, et al.An improved quantum particle swarm optimization and its application in system identification[J].Proceedings of the CSEE.,2011, 31(20):114-122. [11] 沈佳宁,孙俊,须文波.运用QPSO算法进行系统辨别的研究[J].计算机工程与应用,2009,45(9):67-70. SHEN Jia-ning, SUN Jun, XU Wen-bo.System identification based on QPSO algorithm[J].Computer Engineering and Application, 2009, 45(9): 67-70. [12] 王峰,邢科义,徐小平.系统辨识的粒子群优化算法[J].西安交通大学学报, 2009(2):116-120. WANG Feng, XING Ke-yi, XU Xiao-ping.A system identification method using particle swarm optimization[J].Journal of Xi’an Jiaotong University, 2009(2):116-120. [13] 许东文,贾春玉,崔艳超,等.基于量子粒子群算法的BP网络板型模式识别研究[J].燕山大学学报, 2011,35(1): 35-39. XU Dong-wen, JIA Chun-yu, CUI Yan-chao, et al.Study on BP network flatness pattern recognition based on quantum particle swarm optimization algorithm[J].Journal of Yanshan University,2011,35(1):35-39. [14] 徐小平,钱富才,刘丁,等.基于PSO算法的系统辨识方法[J].系统仿真学报,2008(13):3525-3528. XU Xiao-ping, QIAN Fu-cai, LIU Ding, et al.Method of system identification based on PSO algorithm[J].Journal of System Simulation, 2008(13): 3525-3528. [15] 许少华,王浩,王颖,等.一种改进的量子粒子群优化算法及其应用[J].计算机工程与应用,2011,47(20):34-37. XU Shao-hua, WANG Hao, WANG Ying, et al.Improved quantum particle swarm optimization algorithm and its application[J].Computer Engineering and Applications, 2011, 47(20):34-37. [16] 曹树谦,张文德,萧龙翔.振动结构模态分析-理论实验与应用[M].天津:天津大学出版社,2001:35-40.3 QPSO识别结构模态参数

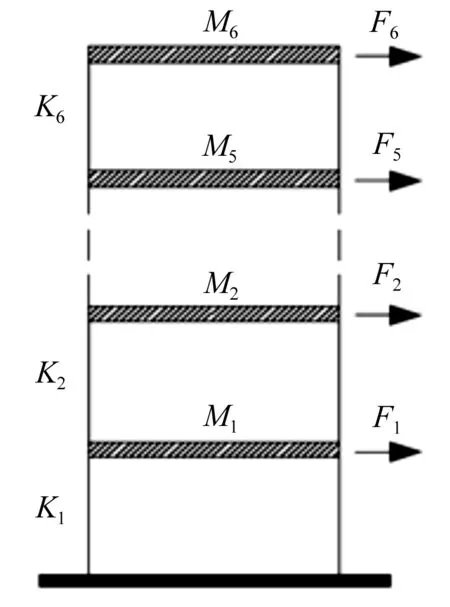
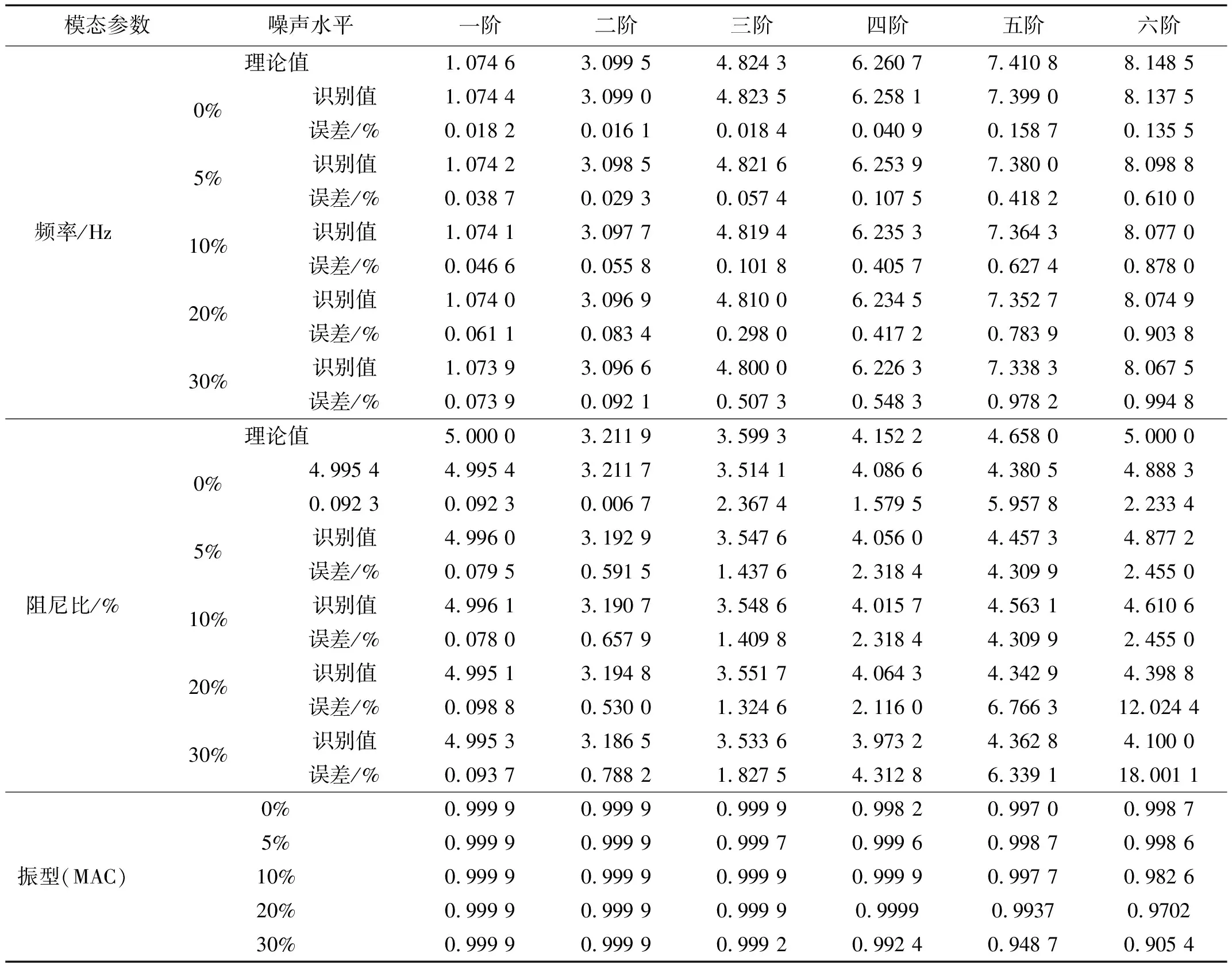
4 实例分析




5 结 论
