鼠笼弹支-金属橡胶阻尼器刚度阻尼优化设计

， ，

(南京航空航天大学机电学院，江苏 南京 210016)

鼠笼弹支-金属橡胶阻尼器刚度阻尼优化设计

张发品，周瑾，金超武

(南京航空航天大学机电学院，江苏 南京 210016)

0 引言

磁悬浮轴承作为一种新型高性能轴承，由于与转子间无接触，使其相较于传统轴承具有转速高和功耗小等许多优点[1]，但磁悬浮轴承对自身刚度阻尼的调节范围较窄，尤其阻尼相对较低，在系统接近或越过弯曲临界转速时，容易因转子振幅过大而发生碰磨导致破坏[2-3]。金属橡胶作为一种既具有所选金属耐高低温等固有特性，又有着普通橡胶弹性的均质多孔材料，能够提供良好的阻尼减振效果，是解决特殊环境下阻尼减振难题的一种新型材料[4]。已有研究表明，合理的外弹性支承可以有效抑制系统振幅，并同时提高系统稳定性，即要减小系统的振幅，可以通过外加合适的刚度阻尼结构来实现[5]。因此，考虑采用鼠笼弹支和金属橡胶组合而成的结构，来抑制磁悬浮轴承系统的振动。该结构不同于传统挤压油膜阻尼器(SFD)，是一种无油润滑转子弹性支承阻尼结构，可以避免SFD由于设计加工不当而可能导致的双稳态、锁死及非协调进动等不利现象[6]。由鼠笼弹支提供主要的支承刚度，金属橡胶提供小部分刚度和全部阻尼，两者刚度并联，因此，该结构的总刚度为鼠笼刚度与金属橡胶环刚度之和，可以保证该结构在较大挤压变形范围内金属橡胶刚度发生较大变化时,依然能够具有良好的线性支承刚度，并且借助于金属橡胶阻尼元件，使该结构同时具有稳定的阻尼性能，可以有效降低转子过临界振幅，提高系统稳定性。

1 鼠笼弹支-金属橡胶阻尼器

支承磁悬浮轴承的鼠笼弹支-金属橡胶阻尼器装置如图1所示。在旋转过程中，因不平衡质量等原因转子会产生涡动，磁悬浮轴承亦会随着转子涡动，进而带动鼠笼弹支发生径向位移并对金属橡胶环产生挤压作用。通过合理选择阻尼器的刚度和阻尼，一方面可为转子系统提供较大变形范围内良好的线性支承刚度，另一方面可以为系统提供阻尼，抑制其过临界振幅，提高运行稳定性。

图1 鼠笼弹支-金属橡胶阻尼器装置

2 支承在阻尼器上转子系统建模

转子系统为两端磁悬浮轴承支承，并在两轴承处外置阻尼器进行减振。利用ANSYS有限元法对支承在阻尼器上的磁悬浮转子系统动态特性进行分析，其有限元模型如图2所示。共有111个节点和110个梁单元，并将磁悬浮支承简化成集中支承作用在节点18和节点97处。图2中,M0和K0分别表示在对应节点处加入了集中质量单元和弹簧单元。以K1和K2分别表示磁悬浮轴承与阻尼器的等效支承刚度，C1和C2分别表示磁悬浮轴承与阻尼器的等效阻尼，M表示磁悬浮轴承的质量，则支承在阻尼器上的转子系统基本数学模型如图3所示。

图2 转子系统有限元模型

图3 转子系统基本数学模型

3 转子系统响应分析

取磁悬浮轴承支承刚度K1=5×106N/m，阻尼C1=700N·s/m，并基于ANSYS的转子动力学模块，得到无阻尼器时转子系统坎贝尔如图4所示。由图4得前四阶临界转速对应频率，如表1所示。

图4 转子在仅支承于磁悬浮轴承时的坎贝尔图

表1 转子系统无阻尼器下前四阶固有频率 Hz

阶次一二三四频率259 1428 0598 61275 0

查看振型图可知，表1中前四阶固有频率分别对应转子系统的平动、锥动、一弯及二弯临界转速。取转子系统工作频域为[0,1000Hz]，则结合表1知，在此区间内系统存在平动、锥动和一弯这前三阶临界转速。

在节点13，节点68处分别加入大小为7.5×10-6kg·m的不平衡量，经ANSYS仿真得出磁悬浮轴承支承节点18处在此频域内无阻尼器下的稳态响应曲线，如图5所示。

图5 节点18在无阻尼器下的稳态响应

由图5可知，在此频域内无阻尼器支承时节点18存在2个响应峰值，分别于258 Hz和604Hz处取得，对应由坎贝尔图分析得到的平动和一弯固有频率，在锥动固有频率处未引起响应峰值。以Up和U1w分别表示平动和一弯幅值。

4 优化方案

磁悬浮转子系统在运转过弯曲临界转速时，转子会发生横向弯曲变形，若变形量过大，长时间运行易造成转子破坏，甚至引发事故，而通过为转子系统外置阻尼器进行减振的首要目标，即是控制工作转速范围内系统弯曲临界转速处的振幅大小。另外，还需要统筹考虑工作转速范围内的各阶不平衡响应。以整体响应品质Us来表示各阶响应峰值的和值，其表达式为：

表2 节点18处各区间不平衡响应的U1w及Us最小值 m

n为分析频域内所有响应峰值的个数；Ui为第i个响应峰值的大小。

经以上分析，确定阻尼器刚度和阻尼的优化方案，使转子系统在工作转速范围内，有尽量小的弯曲响应幅值和整体响应品质。

由上节可知，转子系统在0～1000Hz工作频域内，存在平动和一弯临界转速对应的2个响应峰值，即Up和U1w，则Us=Up+U1w。在K1和C1不变的情况下，U1w及Us均为K2和C2的函数。因此，优化的数学模型为：

minU1w和minUs为优化目标，K2和C2为优化参数。

取刚度优化取值区间为1.0×106～1.0×109N/m，阻尼优化取值区间为100～1.0×105N·s/m。此为多目标多变量优化问题，对于目标函数的凹凸性未知，同时变量的变化范围较大，若在全区间范围建立响应面，则不易观察系统在刚度和阻尼低数量级时的响应特征，在此选用分区间寻优处理的方法，对于刚度和阻尼按照数量级进行区间划分。

5 优化过程及结果

在确定优化方案后，优化工作基于ANSYS Workbench的优化模块Design Exploration完成。借助该模块，在建立响应面的基础上采用目标驱动优化(GDO)设计。程序提供了多种优化算法，由于MOGA(multi-objective genetic algorithm)多目标遗传算法能够快速自动找到最优参数，可有效提高优化效率，因此，选取MOGA算法进行优化。

优化时以U1w及Us的最小值作为目标函数，且将前者权重比调为最高，后者权重比调为一般，求解得各区间U1w及Us最小值，如表2所示。

由表2可知，在[0,1000Hz]内，U1w最小值为7.396×10-7m，在刚度范围[1.0×106N/m,1.0×107N/m]，阻尼范围[100N·s/m, 1000N·s/m]内取得，且区间内Us的最小值为3.877×10-5m；Us最小值为1.942×10-5m，在刚度范围[1.0×106N/m,1.0×107N/m]，阻尼范围为[1000N·s/m,10000N·s/m]内取得，且该区间内U1w的最小值为8.218×10-6m。对比前后2个区间可见，一弯响应最小值的差值较小，但整体响应品质最小值变化明显，前者大小约为后者的2倍。因此，从Us取最小值时所在的区间内选取阻尼器刚度和阻尼的优化解。

在该区间内，程序自动产生的K2和C2的优化推荐解如表3所示。通过完全二阶多项式法拟合出该区间内，一弯幅值U1w以及整体响应品质Us关于阻尼器刚度K2、阻尼C2的响应面，如图6和图7所示。

结合该区间内U1w和Us关于刚度K2、阻尼C2的响应面以及系统所给出的优化推荐解，选取推荐解C作为最终优化解，即取阻尼器刚度K2=3.6×106N/m，阻尼C2=2010N·s/m，此时系统的不平衡响应可取得最佳的抑制效果。

表3 Us取到最小值所在区间的推荐解

K2/(N·m-1)C2/(N·s·m-1)minU1w/mminUs/m权重比——高默认推荐解A1 41×1062134 28 51×10-61 48×10-5推荐解B2 59×1062297 58 39×10-61 68×10-5推荐解C3 56×1062010 98 22×10-61 94×10-5

图6 一阶弯曲响应U1w关于K2，C2的响应面

图7 整体响应品质Us关于K2，C2的响应面

6 阻尼器减振效果分析

取上节所得优化后阻尼器刚度K2=3.6×106N/m，阻尼C2=2010N·s/m，并取磁悬浮轴承刚度K1=5.0×106N/m，阻尼C1=700N·s/m作为仿真边界条件，利用有限元法得到引入阻尼器前后转子系统支承节点18处的稳态响应对比曲线(分析阻尼器对转子系统的减振效果)，如图8所示。

由图8可以看出，在引入阻尼器后，转子系统的平动幅值由2.71×10-5m减小为1.08×10-5m，一弯响应幅值由1.40×10-5m减小为8.23×10-6m，减幅分别为60.1%，41.2%，系统整体响应品质由4.11×10-5m减小为1.903×10-5m，减幅53.7%。可见，所设计阻尼器的引入能够有效抑制转子系统的振动。

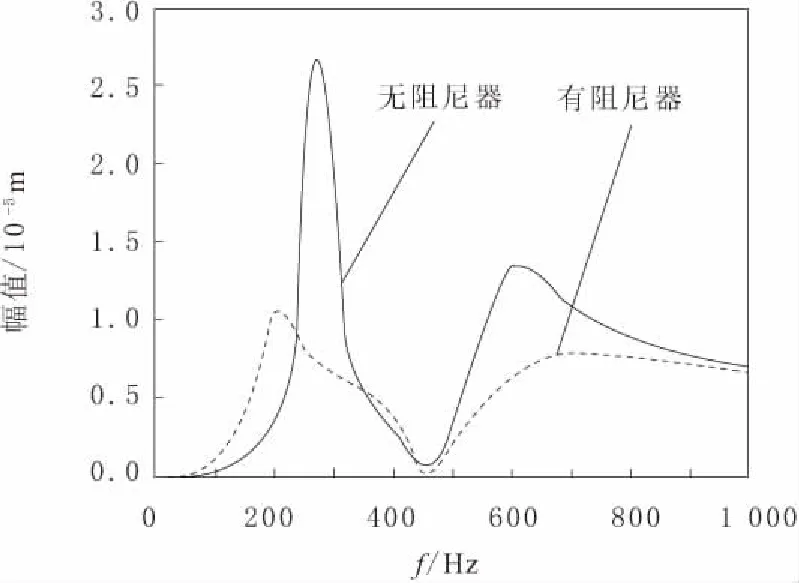
图8 节点18处有无阻尼器支承系统稳态响应比较

7 结束语

对于含有多个支承参数及多个优化目标的优化问题，基于ANSYS Workbench的Design Exploration模块进行目标驱动优化(GDO)设计是十分有效的。阻尼器的刚度和阻尼存在最优值。通过优选阻尼器的刚度和阻尼，可以大大降低系统的不平衡响应幅值，使系统振动得到有效抑制。

[1] 林吉凯. 支承条件的改变对磁轴承系统动态特性影响的研究[D].南京: 南京航空航天大学, 2009.

[2] Yu Suyuan, Yang Guojun, Shi Lei.Application and research of the active magnetic bearing in the nuclear power plant of high temperature reactor[C]//Proc.of the 10th Int.Symp.on Magnetic Bearings. Martigny: ETH, 2006.

[3] Kai A, Christoph S, Rainer N. Active balancing of a supercritical rotor on active magnetic bearings[C]//Proc. of the 10th Int. Symp. on Magnetic Bearings. Martigny: ETH,2006.

[4] Чев Д·Е切戈. 金属橡胶构件的设计[M].北京: 国防工业出版社, 2000.

[5] 徐 华, 孙铁绳, 陈 刚.挤压油膜阻尼器对滑动轴承-转子系统的影响[J].润滑与密封, 2007, 32(6): 19-22.

[6] Yu T B, Jiang Z, Gong Y D, et al.Experiment on stiffness of squeeze film damper for deep hole machining [J]. Journal of Northeastern University (Natural Science), 2002, 23(6): 577-580.

Optimal Design of Stiffness and Damper of Squirrel Cage ElasticSupport-metal Rubber Damper

ZHANGFapin,ZHOUJin,JINChaowu

(College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China)

将一种鼠笼弹支-金属橡胶阻尼器装置应用于磁悬浮转子系统振动的抑制。基于有限元分析软件ANSYS Workbench的Design Exploration模块，以系统的不平衡响应为目标函数，利用多目标遗传算法对该装置的刚度阻尼进行优化设计。从仿真结果来看，优化后的阻尼器装置使转子系统平动及一弯振幅分别降低60.1%，41.2%，可以有效抑制系统振动。

振动控制;鼠笼弹支;金属橡胶;优化设计

A squirrel cage elastic support-metal rubber damper used for vibration control of the magnetic suspension bearing rotor system is designed. Based on the Design Exploration module of ANSYS Workbench，the stiffness and damping of the damper are optimized to minimum the unbalance response of the system with multi-objective genetic algorithms. The simulation results show that the translational and the first bending critical speed can be effectively reduced by 60.1% and 41.2%, that is, the vibration characteristics can be improved effectively after the optimization.

vibration control; squirrel cage elastic support; metal rubber; optimization design

2014-02-17

航空科学基金资助项目(20125752056);江苏省自然科学基金资助项目(BK2011070)

V214.9

A

1001-2257(2014)09-0019-04

张发品(1987-)，男，山东济宁人，硕士研究生，研究方向为磁悬浮技术;周瑾(1972-)，女，江苏徐州人，博士，教授，研究方向为磁悬浮技术、转子动力学、机电系统控制。