气动机械手轨迹的Terminal滑模控制方法

，，

(昆明理工大学机电工程学院，云南 昆明 650500)

气动机械手轨迹的Terminal滑模控制方法

丘世因，袁锐波，易鹏

(昆明理工大学机电工程学院，云南 昆明 650500)

应用Terminal滑模控制方法对三轴直角坐标型气动机械手进行连续轨迹控制。首先建立了气动位置伺服系统的数学模型，然后运用Terminal滑模控制对机械手进行轨迹控制。仿真研究结果表明，采用高阶非线性的Terminal滑模控制方法，可以使该机械手对空间直线轨迹的跟踪误差只在未达到收敛点的时间段内较大，在到达收敛点后能完全跟踪目标轨迹。

直角坐标型机械手；气动位置伺服系统；Terminal滑模；轨迹跟踪控制

0 引言

机械手的轨迹跟踪包含2个方面的问题，一是轨迹规划问题，二是轨迹控制问题。主要讨论轨迹控制问题，轨迹控制的关键是控制方法，轨迹控制的目标是使机械手能保持实时、准确和稳定的轨迹跟踪，国内外众多学者对轨迹控制方法进行了研究。

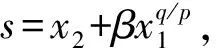
1 气动位置伺服系统建模

1.1 阀控缸建模分析

研究直角坐标三轴气动机械手3个方向的位移输出是阀控缸的位移。以其中一轴为例，其控制系统框图如图1所示。图中微机接口电路中的数字I/O，D/A或A/D转换器由于其固有频率比阀控缸要高很多，而系统性能主要决定于相对低频元器件的特性，高频元器件对它的影响并不大，故此处可以将其忽略，只着重考虑阀控缸的数学模型。

图1 气动控制系统

为简化模型，系统还应作如下假设[5]：系统所用工作介质为理想气体，满足理想气体状态方程；供气压力和大气压力恒定，温度不变；气动系统中空气流动状态为等熵(可逆绝热)过程；气缸内外的泄漏均忽略不计；气缸中气体是均匀的，每一瞬时腔内各点参数相等；动态过程中，各参量的变化是一微小量。

在负载力FL为零，忽略库伦摩擦力Fj影响的条件下，根据气缸力平衡方程和气缸能量方程，可得气动位置伺服系统的传递函数为：

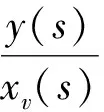
(1)

1.2 系统参数

气动机械手各元件参数可查阅说明书和测量获得。计算得到三轴开环传递函数为:

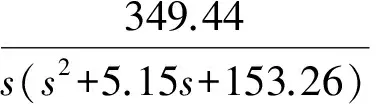
(2)

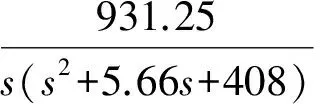
(3)

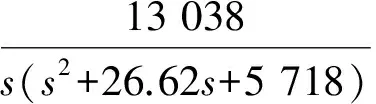
(4)

它们各自在时域内的动态特性曲线分别如图2～图4所示。控制三轴运动的阀控缸系统的阶跃响应无超调，其上升时间分别为tr1=0.706s，tr2=0.964 s，tr3=0.95s；调整时间分别为ts1=1.8s，ts2=7.72s，ts3=1.7 s。

从图2～图4中分析可知，3根轴的动态特性的主要缺点在于响应快速性不够，前2轴上升过程还存在着一定范围的振荡，这些都严重影响了各轴运动的动态特性，降低机械手整体性能。系统的性能取决于开环增益K，阻尼比ξ及固有频率ω，但这3个因素是相互影响的，而且系统中的大多参数在系统组建后基本固定，即使少许参数可以变化，这些变化可能引起机械手其他元件的匹配参数发生变化，增加了研发成本，故需从其他角度寻求提高系统性能的途径。

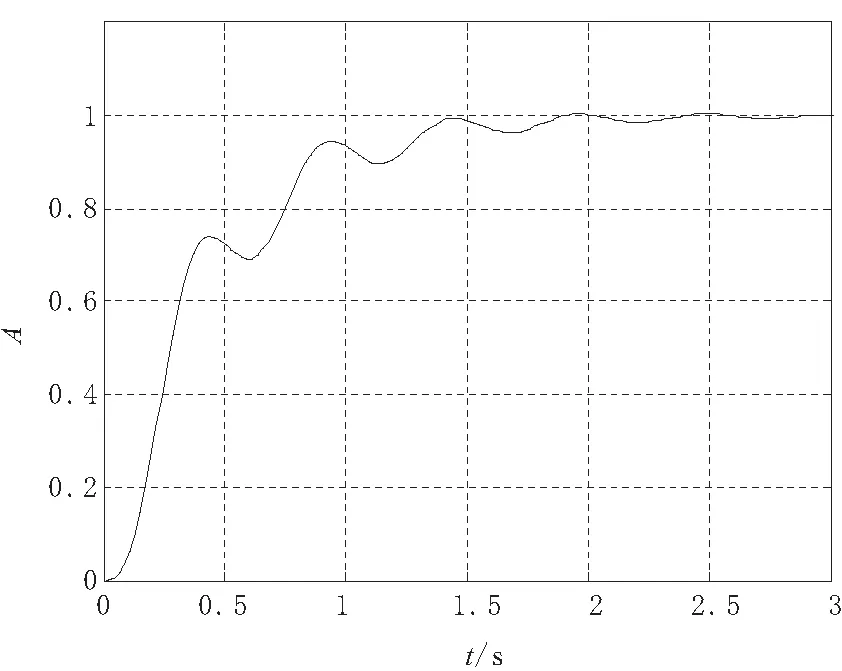
图2 第1轴单位阶跃响应

图3 第2轴单位阶跃响应

图4 第3轴单位阶跃响应

2 高阶非线性系统的Terminal滑模控制器设计

滑模控制不需要精确的数学模型，还具有对外干扰和未建模等因素的不灵敏性。因此，应用一种高阶非线性系统的Terminal滑模控制方法设计控制器。考虑n阶的多输入多输出控制系统为：

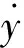
(5)

y∈Rm为输出向量；u∈Rm为输入向量；f∈Rm和b∈Rm×m为已知的系统状态非线性函数矩阵；rank(b)=m；Δf和d(t)分别表示未知对象的不确定性和外部扰动。

(6)

设计滑模面方程为：

σ(X,t)=CE-W(t)

(7)

C=[C1,C2,…,Cn]为矩阵;Ci=diag(ci1,ci2,…,cim);cij=(i=1,2,…,n;j=1,2,…,m)是正常数。

W(t)=CP(t)

(8)

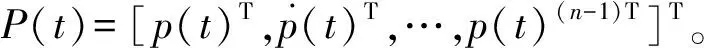
(9)

系数ail可通过假设条件求得，对n阶系统也不失一般性。

根据以上分析，将系统传递函数写成为：

根据系统的传递函数(式(2)～式(4))，得到其相应的非线性状态矩阵为：

令

C=[C1C2C3]

则可设计滑模面为:

(10)

设定三轴跟踪位移目标曲线分别为x11d,x21d,x31d。则控制器输出为：

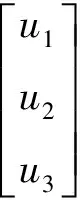
(11)

3 仿真分析

利用Matlab为系统搭建的Terminal滑模控制仿真模型如图5所示。利用Terminal滑模控制器对三轴气动机械手进行空间直线轨迹控制，从图6的仿真结果中可以看出，采用Terminal控制器对系统进行控制时，系统对空间直线轨迹的最大跟踪误差为9 mm，但持续时间短暂。当系统到达收敛点后则能够控制机械手对空间直线轨迹的完全跟踪。

图5 Terminal滑模仿真模型

图6 空间直线轨迹跟踪误差

4 结束语

空间直线轨迹跟踪仿真结果表明，系统只在短暂的收敛时间点前存在跟踪误差，随后能实现对轨迹的完全跟踪，应用Terminal滑模控制能有效实现机械手的高精度轨迹控制。由于直角坐标型气动机械手多用于执行工业生产任务，为满足更多工艺目的，还需要对直角坐标型气动机械手的空间圆弧轨迹、空间任意复杂轨迹进行规划和控制的研究。由于本文Terminal滑模控制思想的本身方法所限，系统不管处于何种初始状态，在到达滑模面前都会有跟踪误差，这个误差有时甚至会超出可接受范围，下一步的研究中可将Terminal滑模控制与其他控制思想结合以进一步提高控制器的性能。

[1] MAN Zhihong,YU Xinghuo.Terminal sliding mode control of MIMO linear systems[J].IEEE Trans On Circuits and Systems-I:Fundamental Theory and Applications,1997,44(11):1065-1070.

[2] MAN Zhihong,YU Xinghuo.Fast terminal sliding mode control design for nonlinear dynamical systems[J].IEEE Trans on Circuits and Systems-I:Fundamental Theory and Applications,2002,49(2):261-264.

[3] YONG Feng,YU Xinghuo,MAN Zhihong.Non-singular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(2):2159-2167.

[4] 刘云峰,陈斌文,缪栋,等.具有强鲁棒性的滑模变结构控制[J].信息与控制,2008,37(2):140-145.

[5] 郑洪生.气压传动与控制[M].北京:机械工业出版社,1988.

Trajectory Control for Cartesian Pneumatic Manipulator Using the Terminal Sliding Mode Control Method

QIUShiyin,YUANRuibo,YIPeng

(Faculty of Mechanical and Electrical Engineering，Kunming University of Science and Technology，Kunming 650500,China)

This paper applies the terminal sliding mode control method to control the trajectory of a three axises cartesian pneumatic manipulator.A mathematical model of the pneumatic servo control system was established at first,then the terminal sliding mode control method was used for trajectory control.The simulation results shows that the tracking error of the terminal sliding mode control method become large only in the time period of not fully reaching the convergence point in time when the manipulator tracks the space straight line,whereas it can fully track the target trajectory after reaching the convergence point.

cartesian-coordinate manipulator;pneumatic servo control system;Terminal sliding mode;trajectory tracking control

2014-01-08

云南省自然科学基金重点项目(2010CD030)

TH137

A

1001-2257(2014)08-0070-04

丘世因(1990-)，男，云南昆明人，硕士研究生，研究方向为流体传动与控制；袁锐波(1968-)，男，云南昆明人，博士，教授，研究方向为电液比例伺服控制、气动伺服控制。