基于图像特征偏差的姿态调整策略研究

，，

(哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150000)

基于图像特征偏差的姿态调整策略研究

刘延杰，景亚宁，隋聪颖

(哈尔滨工业大学机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150000)

为了实现对泡沫柱空间姿态的调整，研究了基于双路视觉的泡沫柱空间位姿调整策略，建立了系统的运动学模型，在此基础上，提出了基于图像特征偏差的位姿调整策略。在仿真分析中，推导了基于Broyden方法的图像雅可比矩阵在线估计方程，建立了系统的运动学模型与视觉成像模型，设计采用了比例控制器。仿真结果表明，采用的图像雅可比矩阵估计方法可以很好地跟踪目标图像特征，图像特征偏差可以快速收敛到设定要求。

姿态调整；图像特征；图像雅可比矩阵；Broyden方法

0 引言

现阶段微操作机器人越来越多地应用在医疗，微装配系统等相关领域。为了实现高精度的微操作要求，微操作系统常需要采用显微视觉。视觉系统作为非接触测量实现了控制的闭环，视觉伺服方法按照误差定义的不同分为基于位置的视觉伺服和基于图像的视觉伺服2种[1]。在视觉伺服系统中，为了避免复杂的标定过程，以及实现更高的操作精度，视觉伺服常采用图像雅可比矩阵在线估计[2-4]的方法完成系统操作。参考文献[5]利用基于Broyden的非线性优化方法实现了对图像雅可比矩阵的在线估计。基于泡沫柱半自动装配系统模型，采用Broyden方法在线估计图像雅可比矩阵，设计了比例反馈控制器，根据图像特征偏差控制系统关节运动，通过仿真分析，验证了该方法的可行性，可以很好的跟踪要求的图像特征，快速消除图像特征偏差。

1 泡沫柱半自动装配系统

泡沫柱半自动装配系统是为了完成泡沫柱与丝阵负载孔的装配任务，在本体设计中，采用正交双路显微视觉来实现对泡沫柱空间位姿的识别，位姿调整平台采用高精度步进电机串联的形式实现对泡沫柱空间位姿的调整，设计的泡沫柱微装配系统如图1所示。泡沫柱位姿调整模块包含5个电动平台，分别控制X，Y，Z3个自由度的直线运动以及绕X,Y轴的摆动自由度θx，θy。左臂位姿调整平台XYZ轴的定位精度≤5μm，分辨率为1μm/脉冲，旋转平台的行程为360°和6°，往返定位精度≤0.003°，分辨率为0.0009°/脉冲，左臂末端安装泡沫柱夹具，真空吸附实现对泡沫柱的粗定位。

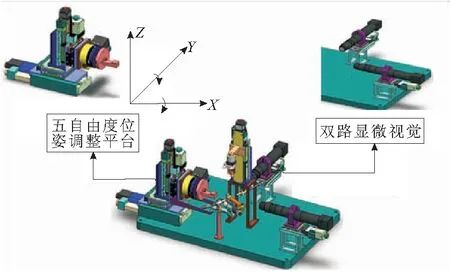
图1 泡沫柱微装配系统模型

左臂位姿调整平台XYZ轴的定位精度≤5μm，分辨率为1μm/脉冲，旋转平台的行程为360°和6°，往返定位精度≤0.003°，分辨率为0.0009°/脉冲，左臂末端安装泡沫柱夹具，真空吸附实现对泡沫柱的粗定位。

双路显微视觉系统用于检测泡沫柱的边缘线的空间姿态，进而确定泡沫柱轴线的空间姿态，系统采用远心镜头，具有高分辨率，超宽景深，极低畸变，无视差的优点。

泡沫柱半自动装配系统装配流程如图2所示。

图2 装配流程

2 位姿调整策略

在装配任务中，需要依次识别泡沫柱的空间位姿，对于泡沫柱和定位杆空间位姿的识别，都可以用通过圆柱体轴线的空间向量来表示。泡沫柱经过夹具的粗定位，轴线空间向量记为n0=[nxnynz]，对泡沫柱空间位姿的调整，就是对轴线空间向量的空间变换。

泡沫柱轴线的空间向量通过正交双路视觉系统获得。

在视觉A,B中，泡沫柱轴线向量在成像平面投影与竖直方向的夹角记为α,β，图示角度方向为正。

泡沫柱的空间姿态用空间向量n0=[nxnynz]表示，向量与偏转角θ,φ的对应关系为:

(1)

泡沫柱轴线的空间向量与双路视觉中偏转角是一一对应关系。

在系统中，泡沫柱轴线姿态的调整由俯仰轴与回转轴完成，变换矩阵分别记为R(y,β)和R(x,α)。调整完成后泡沫柱轴线的空间向量为n=[0 0 1],旋转变换为:

n=R(y,β)·R(x,α)·n0

(2)

联立式(1)与式(2)，可得泡沫柱偏转角θ,φ与位姿调整角α,β之间的对应关系为:

(3)

化简得：

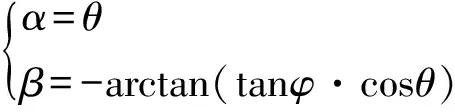
(4)

式(4)求得了位姿调整平台调整角与视觉系统中偏转角之间的对应关系。可以通过偏转角的值来控制位姿调整平台的运动，实现对泡沫柱空间位姿的调整。

3 图像雅可比矩阵在线估计

在第2节的位姿调整过程中，通过运动学模型以及相机模型建立了关节运动量与图像特征变化量之间的函数关系，这个函数关系通常可以以矩阵的形式表示。但是在实际操作中，由于平台装配误差以及镜头成像畸变的存在导致运动学模型与相机模型不准确，往往需要经过复杂的标定，并且重复性较差，无法达到理想的调整精度。

研究了基于图像特征偏差的位姿调整控制策略，其中，基于图像雅可比矩阵的方法在目前视觉伺服中应用非常广泛。

图像雅可比矩阵描述了图像特征变化量与末端执行器在关节空间的速度量之间的映射关系，图像雅可比矩阵为：

(5)

J的含义为:

(6)

图像雅可比矩阵实际是非线性手-眼映射关系在当前位置的线性近似，是一个时变的模型。图像雅可比矩阵可以通过标定参数，然后进行运动学与摄像机模型建模，代入推导的解析式得出，但是不可避免地存在误差，求解精度很大程度上依赖于模型精度和标定精度。

为了避免复杂的矩阵计算与求导过程，避免引入运动学建模与视觉模型标定引入的误差，常采用图像雅可比矩阵的在线估计方法来完成视觉伺服任务。常用的图像雅可比矩阵有以下4种：

a.基于在线自标定的间接估计方法。

b.最小二乘法估计图像雅可比矩阵。

c.Broyden更新法。

d.基于Kalman滤波的图像雅可比矩阵在线估计[6]。

选取图像特征为fe(∶0)=[θ,φ]，期望的图像特征为fe(∶∞)=[0,0]，期望的图像特征随时间变化为0，所以为静态视觉伺服研究。不考虑时间因素，图像特征参数矢量只与位姿调整平台各个关节量有关，记为f(q)，那么图像特征偏差为:

e(q)=f(q)-fe

(7)

对泡沫柱空间位姿的调整目标，就是要图像特征偏差e(q)尽可能取最小值0，也就是求解e(q)=0在局部范围内的收敛解。在求解非线性方程组中，选用Broyden方法来估计图像雅可比矩阵，具有超线性收敛速度。Broyden更新表示为:

(8)

按照式(8)可以构造图像雅可比矩阵的迭代方程为:

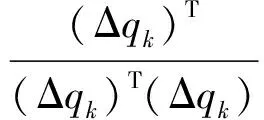
(9)

使用的基于图像特征偏差的位姿调整控制策略框图如图3所示。

图3 位姿调整控制策略

4 仿真分析

为了验证上述控制策略的正确性，以泡沫柱半自动装配系统模型为机械本体，通过Matlab进行了仿真研究，主函数为sita_adjustment.m,其中，运动学模型采用DH法建立，显微视觉系统成像采用小孔成像模型。

在仿真中，通过模块化的m文件分别建立了相应的模型，在主程序sita_adjustment.m中，实现了Broyden在线估计图像雅可比矩阵，以及控制器采用比例环节计算关节增量，其中，Function_Fe_N实现了由图像特征值向空间向量的转换，Function_image_feature实现了平台关节运动角度到图像特征的转换，空间向量的旋转变换如式(3)所示，Function_Inital_Jacobian.m中通过两次试探运动获取了图像雅可比矩阵的初始赋值。

在比例控制中，各个关节的增量并不能任意变化，如果变化过大，可能会超出局部收敛的范围出现震荡或者在其他收敛点收敛，因为在程序中加入了关节运动的归一化处理，设置关节一次性运动限制为5°，当判断关节运动超过限制时，关节增量等比例的缩小，这样既不会影响雅可比矩阵的估计，也可以保证平台运动的稳定，但是，同时由于关节运动角度的限制，会使得消除图像特征偏差所需的迭代次数增大。需要设置迭代终止的条件，通过实时判断图像特征与期望特征的偏差，当偏差image_error小于限定的值时，迭代终止，输出显示“姿态调整完成”,跳出迭代循环。

4.1 阶跃响应

假设初始图像特征为fe=[0,0],给定期望的图像特征为fd=[50,70]，测试系统对于阶跃信号的响应，控制采用比例环节，仿真结果如图4所示。

图4 阶跃信号图像特征跟踪结果

根据图4，对于阶跃信号，仿真系统可以在较小的迭代次数完成无误差跟踪，能满足泡沫柱位姿调整的要求，迭代次数与关节限制有关。

4.2 斜波响应

假设初始图像特征为fe=[0,0],给定期望的图像特征为fd=[k,k]，测试系统对于斜波信号的响应，控制采用比例环节。

迭代次数为100时，仿真结果如图5所示。

图5 斜波信号图像特征跟踪结果

根据图5，对于斜波信号，仿真系统也可以完成角度特征的跟踪任务。

4.3 加速度信号响应

加速度信号跟踪的仿真结果如图6所示，首先将仿真模型中关节运动量限制更改为1000°，系统仍然无法完成跟踪，所以系统不能跟踪加速度信号。通过仿真分析，系统可以跟踪阶跃信号与斜波信号，但是不能跟踪加速度信号，在跟踪阶跃信号时，随着迭代次数的增加，图像特征偏差趋向于0，可以实现无偏差的姿态调整。

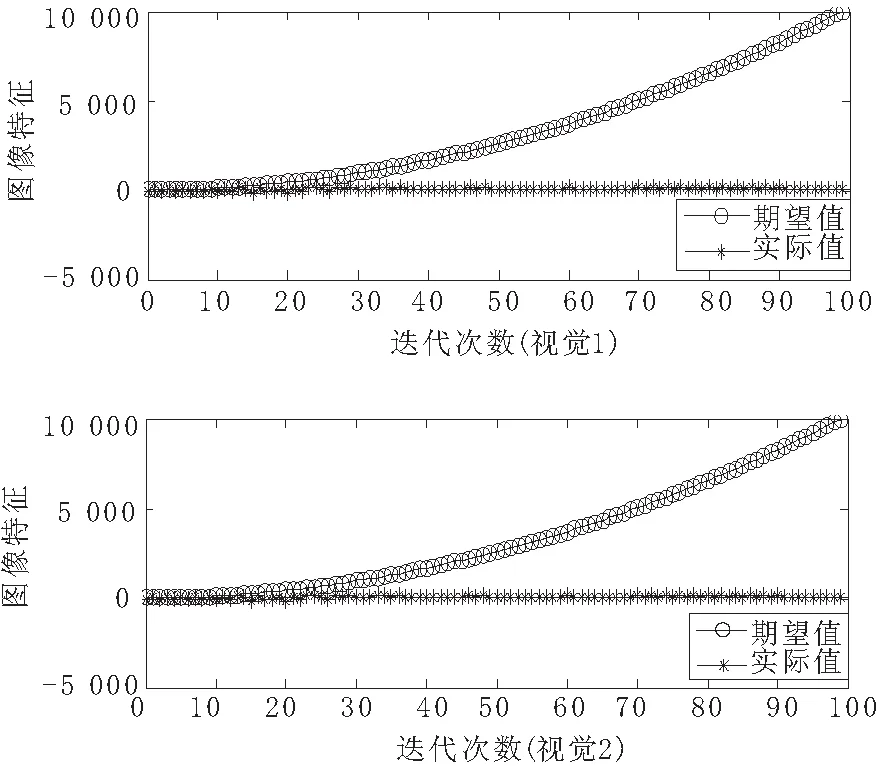
图6 加速度信号跟踪的仿真结果

5 结束语

分析了泡沫柱半自动装配系统的组成原理，重点研究和解决了在双路显微视觉下泡沫柱进行空间位姿调整的问题，提出了基于图像特征偏差的位姿调整控制策略，通过Broyden更新方法完成了图像雅可比矩阵的在线估计，并构建了基于该系统的仿真模型，分别对典型信号进行仿真，仿真结果验证了该方法的有效性，图像特征偏差可以快速收敛到0，该控制算法可以在无标定的泡沫柱位姿调整中应用。

[1] Janabi Shari F,Marey M.A kalman-filter-based method for pose estima-tion in visual servoing[J].IEEE Trans.Robot,26,5,939-947,2010.

[2] Piepmeier J A,McMurray G V,Lipkin H.A dynamic Jacobian estimation method for uncalibrated visual servoing[C]//Proceedings on the 1999 IEEE/ASME International Confe-rence on Advanced Intelligent Mechatronics.Atlanta:IEEE/ASME,1999.944-949.

[3] Su J B，Xi Y G.Uncalibrated hand eye coordination based on auto disturbance reject-ion controller[C].Proceedings of the 41st IEEE Conference on Decision and Contro1,Las Vegas:IEEE,2002.923-924.

[4] Lu C P,Mjolsness E,Hager G D.Online computation of exterior orientation with application to hand-eye calibration[J].Math Comput Model,1996(24):121-143.

[5] Armstrong Piepmeier J,McMurray G,Lipkin H.A dynamic jacobian estimation method for uncalibrated visual servoing[J].in Proc.IEEE/ASME Int. Conf.Adv.Intell.Mechatron.,Sep,1999,944-949.

[6] 刘广瑞,黄真.基于Kalman滤波的图像雅克比矩阵在线估计[J].郑州大学学报工学版,2013,34(1):96-98.

Image-based Research on Posture Adjustment Strategy

LIUYanjie，JINGYaning，SUICongying

(State Key Laboratory of Robotics and System，Harbin Institute of Technology，Harbin 150000,China)

In order to complete the task of foam’s posture adjustment,the study of space posture adjustment strategy based on dual vision is carried on and the system kinematic model is established.Afterwards,a strategy based on image features deviation is proposed.In the simulation analysis,the equation is derived based on image Jacobian matrix online estimation using the method of Broyden in which kinematic model and visual imaging model is established and a proportional controller is designed.The simulation results show that the method of image Jacobian matrix online estimation proposed in this paper can track the target image well and the image feature deviation can quickly converge to the set requirements.

posture adjustment；image features；image Jacobian matrix；broyden method

2014-05-04

国家高技术研究发展计划“八六三”资助项目(2013AA040901);黑龙江省科研机构创新能力提升专项计划项目(YC13D004)

TP24

A

1001-2257(2014)08-0066-04

刘延杰(1975-)，男，教授，黑龙江哈尔滨人，研究方向为机器人技术；景亚宁(1989-)，男，河北石家庄人，硕士研究生，研究方向为微操作。