弹性拉杆在冲击载荷下的力学性能分析

陈凯帆 ，魏小辉,，何思元，聂 宏,，徐 奎

(1.南京航空航天大学 飞行器先进设计技术国防重点学科实验室，江苏 南京 210016)(2.南京航空航天大学 机械机构力学及控制国家重点实验室，江苏 南京 210016)

弹性拉杆在冲击载荷下的力学性能分析

陈凯帆1，魏小辉1,2，何思元1，聂 宏1,2，徐 奎2

(1.南京航空航天大学 飞行器先进设计技术国防重点学科实验室，江苏 南京 210016)(2.南京航空航天大学 机械机构力学及控制国家重点实验室，江苏 南京 210016)

弹性拉杆是某断离机构的重要元件，其在静力载荷和冲击载荷下的力学响应特性尤为关键。采用理论方法和有限元方法分别建立了该弹性拉杆在静力载荷和冲击载荷下的分析模型，得出了其在不同加载速率下的位移响应特性，发现在冲击载荷下弹性拉杆有明显振荡，其位移有0.06mm左右的振幅。进而研究了不同材料对弹性拉杆在冲击载荷下的力学性能的影响，发现在10 000kN/s的加载速率下，现阶段的常用金属材料所表现出的力学性能是一样的，并且与静力载荷下的力学性能相同

弹性拉杆；冲击载荷；力学性能；Patran/Nastran；固有频率；位移函数

在爆炸、冲击等强动载荷的作用下,结构将表现出与准静态情形很不相同的力学行为。材料在受到这种载荷时，意味着高加载率或者高应变率。在冲击载荷中，材料的应变率达到了102～104s-1,甚至106s-1，然而在准静态过程中只有10-5～10-1s-1，所以材料将表现出与准静态不同的力学行为，这是需要好好研究的[1]。

近来已有很多力学工作者对结构在动载作用下的力学特性作了一系列研究。许卫群采用移行铰模型和有限元法分别对结构在冲击载荷下的响应进行了分析[2]；黄顺兵模拟了4种不同实验来研究冲击载荷下的响应问题，并通过模拟结果与试验结果相比较得出，仿真分析的成功在于实际工程结构的有限元模型建立得是否合理与材料模型的选择能否真实反映出结构在不同受力状态下的性能两个元素[3]。但是由于模型的复杂性、时间和其他条件的限制，这些理论研究所建立的理论模型与实际情况存在不少误差，还有需要改进的地方。

本文主要对弹性拉杆进行冲击载荷下的力学性能研究，即利用理论模型计算和有限元软件Patran/Nastran分析其在冲击载荷下的力学性能，并通过改变材料属性来分析其对杆件力学性能的影响。

1 弹性拉杆模型与载荷工况

弹性拉杆的结构示意图如图1所示，其在冲击载荷作用下的变形量是某断离机构的关键技术参数。其材料为300M，弹性模量为1.98×1011N/m2，泊松比为0.3，密度为7 740kg/m3。

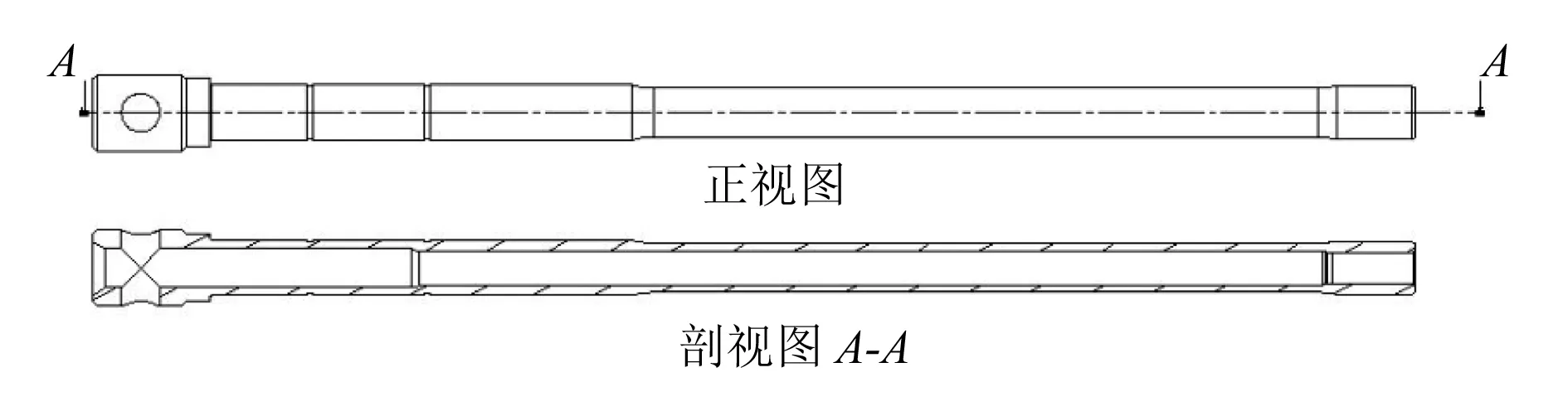
图1 拉力杆模型

此杆件只受轴向载荷，杆的一端固定，一端受载。载荷工况共有5个，第一个工况为缓慢加载，其余4个工况的加载速率不断提高。5个工况的载荷数值相同。载荷情况见表1，其中当力达到最大值时载荷继续保持。

表1 载荷工况

2 简化理论分析方法

首先进行简化理论分析，将这根拉杆模型简化成振动学模型，这里简化为典型的系统力学模型，是一个单自由度系统，包含弹簧、阻尼器和质量块3个基本的元件，不过由于模型只是单纯地受到1个轴向力，所以这里阻尼器可以省略，即只剩下2个基本元件[4]。振动模型如图2所示。

图2 振动模型

然后根据牛顿第二定律可以得出振动方程:

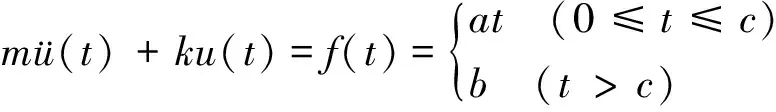
式中：m为此张力杆的质量；a为加载速率；b为加载的力，这里恒为500kN；c为加载到500kN所需要的时间；ü(t)和u(t)分别代表这个质量块的运动加速度和这个质量块的位移。

最后可以得到此振动方程的解:

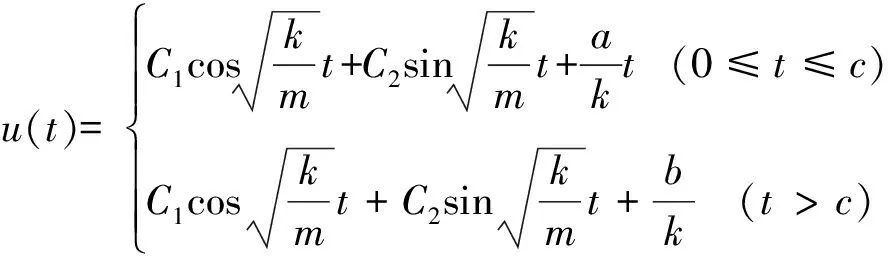
通过两种不同工况来比较冲击载荷下杆的位移函数。这里选择100kN/s与100 000kN/s两种不同加载速率的工况进行比较。首先由固有频率公式可以得到：

然后可以得到C2的值：

在a=100kN/s的情况下，c=5s，此时当t=5时，有:

u(5)=0.001 27u′(5)=0.000 48

可以得出当t=5时，弹性拉杆的重心处的位移为0.001 2m。同时根据这两个初始条件，算出当t≥0.074时的位移表达式中C1,C2的值与此阶段的位移函数：

C1=-5.7×10-10

C2=1.2×10-9

同样的方法，在a=100 000kN/s、c=0.005s的情况下，当t≥0.007 4时，可以算出表达式中的C1，C2的值与此阶段的位移函数：

C1=-2.6×10-5

C2=-5×10-6

3 有限元方法

采用美国Altair公司的有限元分析软件HyperWorks作为前处理软件[5]，美国MSC.Software公司的Nastran作为求解器，Patran作为后处理软件[6]。

最后所建立的有限元模型如图3所示。

图3 有限元模型

4 分析结果及参数影响研究

通过软件计算得出了弹性拉杆在不同工况下的力学性能，最后发现除了在最大加载速率下，其他载荷工况弹性拉杆所表现出的力学性能是一样的，而最大加载速率下，弹性拉杆的应力值会出现振荡现象。这里选取了两种加载速率,即100kN/s与100 000kN/s的工况，重心附近一个节点的应变随时间变化图如图4～6所示。

由理论分析过程可以看出,最后的位移函数就是弹性拉杆重心处的位移函数，现将理论分析的位移函数在MATLAB中作出，其中由于100 000kN/s载荷工况响应时间非常短，因此在这里单独画出，如图7，8所示。

将有限元计算结果与理论分析结果相对比可以看出，将这根弹性拉杆简化成不含阻尼器的典型振动模型是可行的，并且在100 000kN/s以上的加载速率下，弹性拉杆的力学性能与静载或者小速率下的力学性能有着明显的差别。

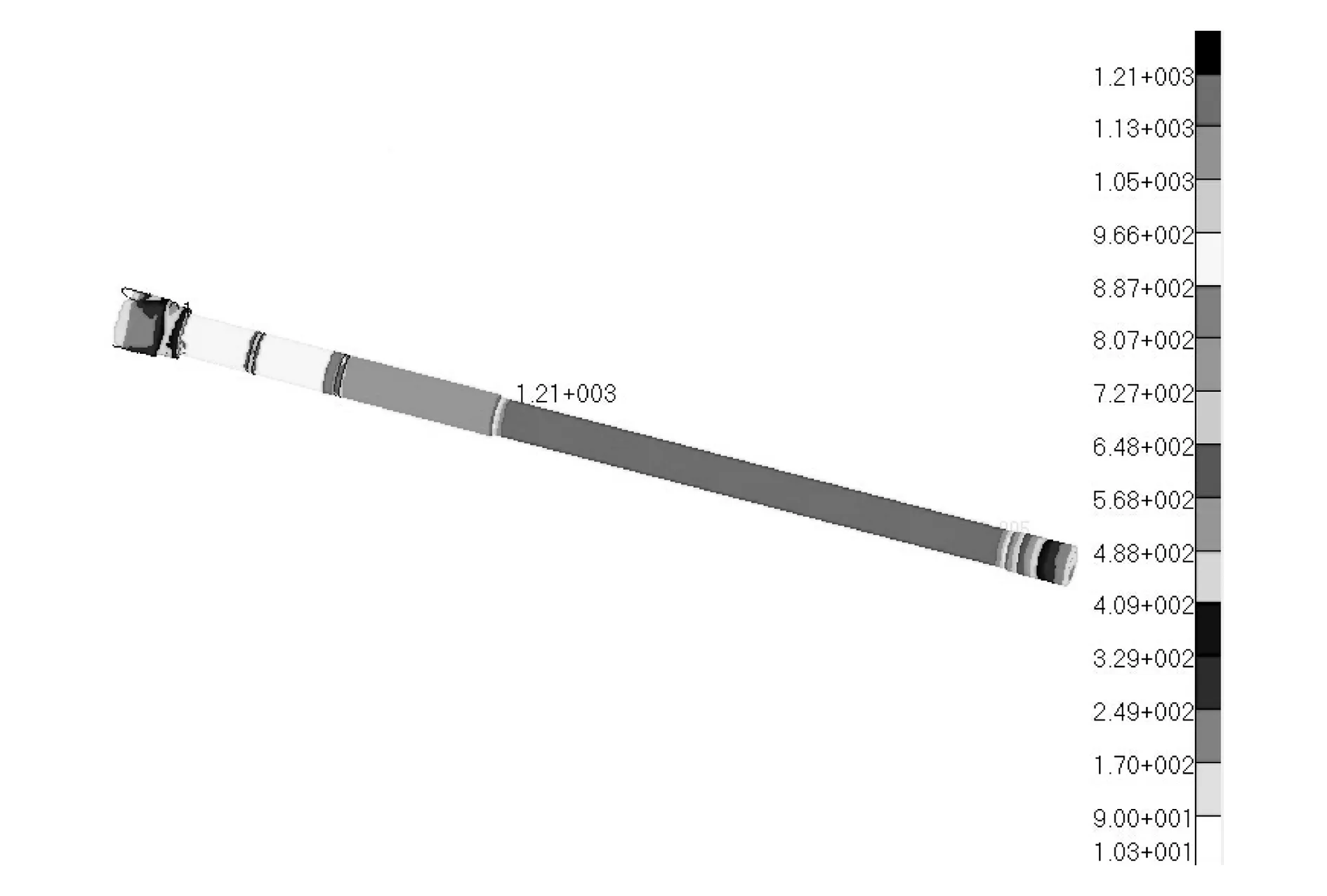
图4 有限元计算结果(100kN/s加载速率)

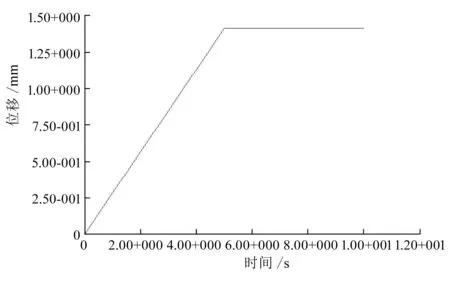
图5 100kN/s工况下应变图

图6 100 000kN/s工况下应变图

图7 100 000kN/s工况下位移函数图

图8 不同加载速率下位移函数图

由位移函数表达式可见材料的固有频率对计算结果的影响很大，固有频率通常由弹性模量和密度来决定。现在通过改变弹性拉杆的固有频率来研究材料属性参数的影响。这里选择一些常用金属材料和固有频率相差比较大的金属材料来进行计算，应力结果见表2[7-8]。

表2 不同材料下的应力结果

从表2可以看出，在常用金属的属性范围内，在加载速率为10 000kN/s、载荷500kN的工况下，这根弹性拉杆所呈现的应力结果是一样的，而且与500kN的静力载荷相一致。

5 结束语

本文首先建立了弹性拉杆的理论振动模型，并计算出其位移函数；然后通过有限元软件计算出其在各种工况下的力学性能；通过改变材料固有频率来研究在一种工况下属性值对弹性拉杆的力学性能影响。最后对于这根弹性拉杆的研究，可以得到以下结论：

a.在加载速率为10 000kN/s以下时，弹性拉杆所表现出的力学性能与在静力载荷下表现出来的一致。在100 000kN/s的加载速率下，在力恒为定值阶段，位移值出现上下波动，有0.06mm的振幅。

b.加载速率的大小影响着弹性拉杆的位移响应时间，加载速率越大，位移响应也就越快。比如100kN/s的加载速率下，位移要到5s的时候才会达到最大值，而100 000kN/s的加载速率下则在0.005s的时候位移就已经达到最大值。

c.用不同的常用金属材料制作成这根弹性拉杆，在所得到的杆的固有频率范围内，给此拉杆加上10 000kN/s的加载速率、500kN的载荷，弹性拉杆最后所受的应力值几乎是一样的，不会因弹性模量或者密度的变化而变化，并且与500kN静载下的应力结果相一致。

[1] 晓青. 冲击动力学[M]. 北京：北京理工大学出版社, 1992.

[2] 许卫群. 冲击载荷作用下机构的动力响应分析[D].武汉：武汉理工大学，2004.

[3] 黄顺兵. 冲击载荷下有限元原理及热效应分析[D].南京：南京理工大学，2014.

[4] 胡海岩. 机械振动基础[M].北京：北京航空航天大学出版社，2005.

[5] 张胜兰. 基于HyperWorks的结构优化设计技术[M]. 北京:机械工业出版社, 2007.

[6] 刘兵山, 黄聪. Patran从入门到精通[M]. 北京:中国水利水电出版社,2003.

[7] Zhang H W, Zhang L. The parametric variational principle and finite element method for material with different modulus in tension and compression[J].GongchengLixue/Engineering Mechanics,2012,29 (8):22-27，38.

[8] 柯尊凤，邓华容.短应力线轧机拉杆有限元分析[J].冶金设备，2010(6)：35-46.

Analysisonthemechanicalpropertiesofelasticbarinimpulsiveload

CHEN Kaifan, WEI Xiaohui, HE Siyuan, NIE Hong, XU Kui

(Nanjing University of Aeronautics & Astronautics, Jiangsu Nanjing, 210016, China)

Elastic bar is an important element in the disconnection mechanism, and its mechanical response properties in basic load and impulsive load conditions are especially critical. This paper establishes the analysis models of this elastic bar in basic load and impulsive load conditions separately with theoretical method and finite element method respectively, which helps elicit the mechanical response properties of this bar at different loading rates and witnesses its obvious vibration in impulsive load, the amplitude of displacement is about 0.06mm. In addition, it analyzes the influences of different materials on the mechanical properties of this bar in impulsive load, the results show that the metal materials commonly used at the present stage are same mechanical properties at the loading rate of 10 000kN/s. These mechanical properties present the same as shown in basic load.

tension bar; impulsive load; mechanical properties; patran/nastran; natural frequency; displacement function

10.3969/j.issn.2095-509X.2014.12.008

2014-11-28

国家自然科学基金资助项目(51105197，11372129)；机械结构力学及控制国家重点实验室(南京航空航天大学)自主研究课题资助项目(0214G01)；中央高校基本科研业务费专项资金资助项目(NP2015402);江苏高校优势学科建设工程资助项目

陈凯帆(1990—)，男，江苏盐城人，南京航空航天大学硕士研究生，主要研究方向为飞行器起落装置设计技术。

V229+.3

A

2095-509X(2014)12-0034-04