大型客运站调车机车运用优化研究

涂 瑜，刘 康

(1.大秦铁路股份有限公司太原车务段;2.大秦铁路股份有限公司榆次站)

调机运用计划是客运站到发线、客技线、咽喉等各子系统协调作业的关键，调机牵引车底出入库作业时间决定了始发、终到列车占用到发线、客技线的起止时间，直接决定了始发终到列车的接发情况。因而如何合理组织好调机运用计划，直接关系着铁路客运站作业效率和铁路客运站通过能力的提高。目前，有关学者就客运站调机运用的优化问题，国内外有关专家学者做过的研究相对很少。文献以车底、调机运用、车底停留线为研究对象，利用排序理论，以总晚点数最小为第一目标和调机均衡运用为第二目标建立具有柔性流水作业性质的车底取送模型。文献主要研究编组站调机运用计划具有不同开工、完工时间窗口的单机调度问题，其优化目标是最小化晚点列车的数量，建立单机调度数学模型并采用蚁群算法求解。但需要指出的是，尽管上述模型考虑了虚拟调机、时间窗等因素及多个约束条件，但其仍存在若干问题:只是在日(班)计划的层面考虑调机的均衡使用而未将阶段计划考虑在内;未考虑两相邻车底出入库时刻应满足最小时间间隔;忽略了咽喉区作业的协调(避免交叉干扰);客运站到发线的能力限制问题。

以上相关研究均未涉及调车机车的紧连续以使调车机车充分调用，减少不必要的消耗成本，未考虑调车机车为牵引车底时的空走行程等因素。鉴于此，本文考虑调机空走程数最小，避免不必要的空走行程;调车机车的紧连续等影响因素。建立铁路客运站调车机车运用优化模型，根据所建模型，设计相应算法，以求解该模型，对解决该问题提出较全面的方法。在到发线上出发作业时间标准为Tsf，调机在取、送车底的等待时间为θk，调机取、送车底的时间标准均为T，车底Jj在车底停留线上的时间标准为，最早可能入库时刻和最晚可能出库时刻分别记为、。办理入库作业的调机集合为Z1={Eq│q=1，2，K，K1}，办理出库作业的调机集合为 Z2={Eq│q=1，2，K，K2};调机 Eq(q=1，2，Λ，K)被车底占用次数xq∈{0≤xq≤n，xq∈Z};用eq表示调机Eq是否为虚拟调机，若调机Eq为虚拟调机，则eq=1，否则eq=0。

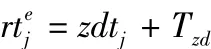
1 调机运用优化模型的建立

此文在既有研究基础上，结合客运站的技术设备和行车作业组织方法，同时考虑以下约束条件:

(1)将调机取送作业的空走行程考虑进去，保证调机空走程数最小，避免不必要的空走行程;

(2)同一到发线接发相邻列车的时间间隔至少要满足最安全时间间隔要求;

(3)考虑客运站到发线的使用能力;

(4)考虑到调车机车的紧连续，以使调车机车充分调用，减少不必要的消耗成本。

(5)非正常情况下的调机优化使用，例如:春运、暑运、旅游高峰期以及设备故障等。

设K为调车机车总台数，f为到发线总条数，Skj为第k台调机取送第j个车底的总走行距离。车底Jj(j=1，2，Λ，n)的到达时刻zdtj和出发时刻sftj都可依据列车运行图确定取值;终到列车在到发线上终到作业时间标准为Tzd，始发列车

此外，因车底出入库作业时间相差不大，可以利用调机Eq被占用次数xk的方差来体现调机使用的均衡性。这种调机使用模型应尽可能保证列车作业正点运行，因此用Dj统计车底Jj所属车次正晚点情况。其中，Dj=1表示车底Jj所属的列车车次不能正点运行;Dj=0表示车底Jj所属的列车车次能够正点运行。

至此，为保证列车经整备后按点始发，本文以列车总晚点数∑Dj最小为第一优化目标(即误工数最少)。以调机均衡使用，即方差最小为第二优化目标建立具有两个处理机中心、缓冲区有限。记为M2(采用国际使用的三参数α│β│γ)，如下式。

则的调机运用优化模型M2:

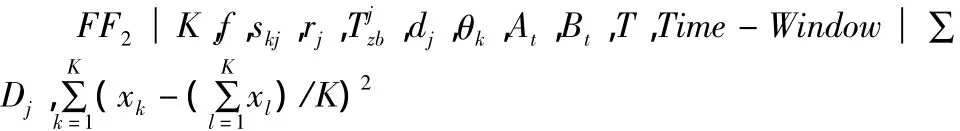
2 算法设计

采用排序方法，对入库车底实行“先到先入库”、出库车底实行“先发先出库”的原则进行合理排序，通过调机的紧接续，制定调机作业计划方案，从而制定更加合理的调机运用方案。

Step1对于入库车底，计算其最早入库时刻x'j，且x'j=rj;对于出库车底，计算其最晚出库时刻y'j，若x'j＜y'j则y'j=dj，否则 y'j=dj+tday

Step3对于入库车底，按其最早入库时刻x'j由先到后进行排序，即 x'j＜ x'j+1时 x'jφx'j+1，否则 x'jπx'j+1;若最早入库时刻相等，则按最晚出库时刻由先到后排序，即x'j=x'j+1且y'j＜ y'j+1时 y'jφy'j+1，反之，则则 y'jπy'j+1，由此构成序列Ⅰ，共n项。

对于出库车底，按其最晚出库时刻y'j由先到后排序，即y'j＜ y'j+1时 y'jφy'j+1，否则 y'jπy'j+1;若最晚出库时刻相等，则按最早入库时刻由先到后排序，即y'j=y'j+1且x'j＜x'j+1时y'jφy'j+1，反之，则，由此构成序列Ⅱ，共n项。

Step4对于序列Ⅰ和序列Ⅱ，按由先到后的顺序排列构成序列Ⅲ，其中相邻的前后两项应满足:y'jπy'j+1或x'jφx'j+1或 y'jφy'j+1或 x'jφy'j+1，共 2n 项。

Step5j=1。

Step6对于序列Ⅲ中的车底Jj。

(1)若Jj来源于序列Ⅰ，则安排调机Ej(Ej∈Z1)，若Ej空闲且占用次数较少，等待时间较长，取送该车底的总走行距离较短，则Ej被占用，修改各调机所处的状态及相应的等待时间θk和调整时间At或Bt，x1=xl+1(El=Ej，“=”表示两者为同一台调机;El∈z)。若没有合适的调机供该车底使用时，则调整车底出入库作业时间，转Step2。

(2)若Jj来源于序列Ⅱ，则安排调机Ej(Ej∈Z2)，若Ej空闲且占用次数较少，等待时间较长，取送该车底的总走行距离较短，则Ej被占用，修改各调机所处的状态及相应的等待时间 θk和调整时间或 At，Bt，Dj=0，j=j+1，若 El=Ej，El∈Z，则xl=xl+1，转Step7。若没有合适的调机供该车底使用(即此时Dj=1)，则调整车底出入库作业时刻，转Step2。

Step7若j≥2n成立，转 Step8;否则，转Step6。

Step8输出调机运用计划，统计∑Dj和S2x。

3 实例

一大型客运站在某日内，有21对始发和终到旅客列车需要办理车底出入库作业;查阅相关铁路资料，铁路规章等可得数据，本文取办理列车的出发作业时间为四十分钟，最少不得小于三十五分钟;办理列车的终到时间为三十分钟，但最小不得少于二十五分钟。取最小车底整备作业时间为三十分钟;取调车机车在整备库和车站之间的运行最小时间为十分钟，此大型客运站拥有调机3台，来进行车底的取送作业;整备库客技线充足，在18:00时刻，D1在整备库，D2、D3在到发场。

制定出的此时段内的车底在该站办理各项作业的计划，其安排结果见表1～表2。

表1内的T968次旅客列车办理相关作业时间较为紧迫为了保证调机的充分运用(T968次办理终到作业计划时间为25min)，在实际操作中应注意加强作业组织从表1～表2中的数据可见，车站调机运用很均衡，利用率较高，列车均能正点运行，能较充分满足现场作业的需要。

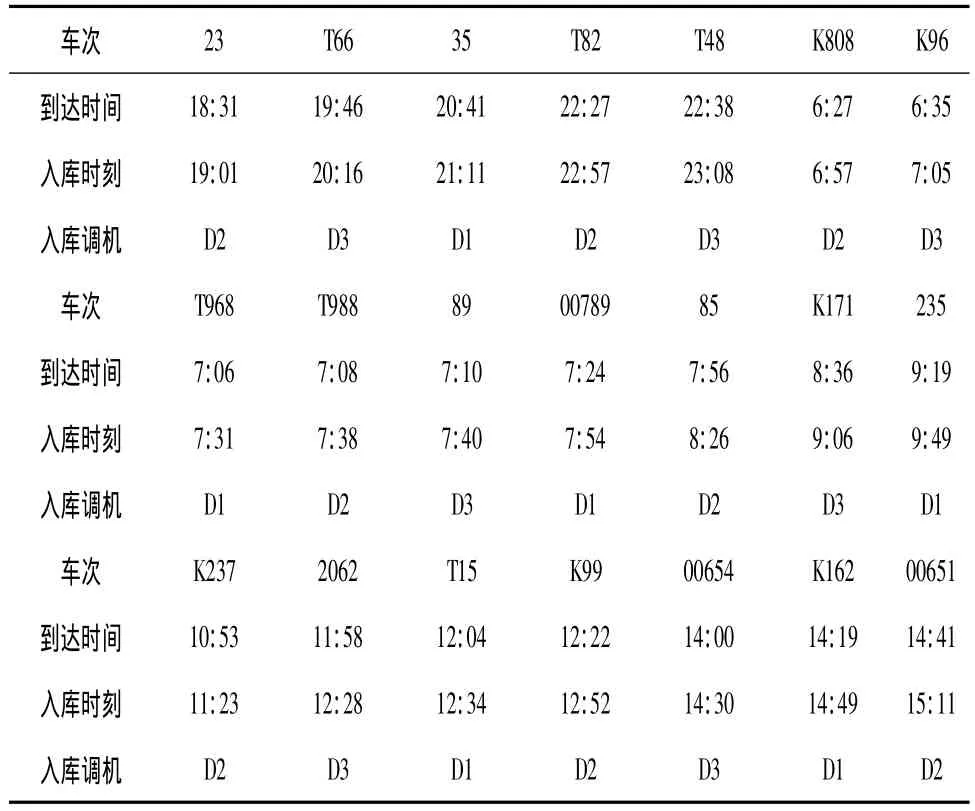
表1 终到旅客列车办理彻底入库作业

表2 始发旅客列车办理车底出库作业

4 结论

通过考虑调车机车的紧连续以使调车机车充分调用，减少不必要的消耗成本，考虑调车机考虑调机空走程数最小，避免不必要的空走行程;调车机车的紧连续等各相关影响因素和约束条件，建立大型客运站调车机车运用优化模型，设计相应算法，解决了旅客列车车底的出入库重要性排序、调机选择，最终给出解决调机均衡使用的优化方法。虽然其中不乏决策者的决策，但目前还是系统地解决了调机安排的工作问题，并对该方案进行了分析。使得解决方案更具科学性。

:

［1］雷定猷，张英贵，刘明翔.铁路客技站车底作业排序模型与算法［J］.铁道学报，2007，29(6):1-6.

［2］王世东，郑力，张智海，田任然.蚁群算法在调机运用计划中的应用［J］.中国铁道科学，2007，28(3):104-108.

［3］谢楚农，黎新华.铁路客运站到发线运用优化研究［J］.中国铁道科学，2004，25(5):130-133.