Gas Leakage Source Localization Algorithm Based on Distributed MMSE Sequential Estimation*

ZHANG Yong，MENGQinghao，WU Yuxiu，ZENGMing

(1.School of Information Engineering，Tianjin University of Commerce，Tianjin 300130，China; 2.School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

Gas Leakage Source Localization Algorithm Based on Distributed MMSE Sequential Estimation*

ZHANG Yong1，2，MENGQinghao2*，WU Yuxiu2，ZENGMing2

(1.School of Information Engineering，Tianjin University of Commerce，Tianjin 300130，China; 2.School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

Distributed gas source localization with Wireless Sensor Networks has an important significance in the environmentalmonitoring，security protection and pollution control and other fields.a gas leakage source localization (GLSL)algorithm based on distributed minimum mean squared error(D－MMSE)sequential estimation is proposed. In the proposed GLSL algorithm，an information fusion objective function which combines the information utility measure and the communication cost between sensor nodes is constructed，and the sensor－node scheduling scheme is designed by optimizing the information fusion objective function;For each selected sensor node，the estimator and the correspondingmean square error are updated with its own observation and the noise corrupted decision from the previous node and transmitted to the next selected node by collaborating information within its neighborhood，and to decrease the energy consumption，the neighborhood radius is adjusted dynamically based on themean square error. At last，the analysis and simulation results show that the proposed algorithm could be applied to the GLSL with a realtively high accuracy，less time and relatively energy consumption compared to the single node sequential estimation algorithm.

wireless sensor networks;MMSE;sequential estimation;gas leakage source localization

无线传感网络(WSN，Wireless Sensor Networks)通过具有感知、计算和无线通信功能的传感器节点采集周围环境信息可完成环境监测、目标源定位与追踪等任务［1］。其中，气体泄漏源定位与跟踪是其在环境监测领域研究的一个热点问题［2－4］。基于无线传感网络的气体泄漏源定位本质是源位置参数识别问题，也可看作源物理扩散建模的求逆问题，通常采用无线传感网络信息处理算法实现［5－6］。WSN中节点能量、感知范围、信号处理能力和通信带宽等资源有限，传统集中式信息处理方法存在稳定性和鲁棒性差问题，因此，近年来对传感网络中非集中式信息处理的研究渐成热点［7－9］。其中文献［7］重点对WSN中分布式节点协作信息处理算法进行了研究并提出了一个理论框架，其思想是网络中的主导节点基于信息熵和网络几何理论调度相关节点，并根据访问信息实现目标源参数估计量及其性能指标的更新与传递。基于分布式信息处理算法并结合环境中气体物理扩散特性在参数估计精度和网络能耗等资源约束条件下设计出高效的气体泄漏源定位算法是该领域研究的重点。

Zhao基于文献［7］的分布式信息处理框架对气体泄漏源定位［10－11］问题进行了研究，文献［10］首先根据泄漏气体的物理扩散模型采用分布式Bayesian序贯估计算法推导出估计量的概率分布函数，然后根据节点测量值求解其估计量的后验概率分布，并将其作为算法的估计性能评价指标实现节点调度与信息更新。该算法在节点之间传递的信息是估计量的后验概率分布。文献［11］则基于分布式极大似然估计方法实现泄漏气体源定位，并采用Fisher信息阵作为估计性能指标，通过对似然函数迭代求解完成节点之间估计量的更新和传递。Keats［12］从气体源物理扩散建模的逆问题求解角度对空气中污染源的各种参数进行测定研究，所用方法也基于信息驱动机制并结合Bayesian序贯估计实现，对比文献［10］其增加了待估参数的数量。Ristic［13］则把信息驱动机制和分布式序贯估计算法应用到了伽马放射源的定位的研究中。

上述几种源定位算法在每个运算周期均采用单个节点依据自身测量值和前节点估计值来实现源参数估计量的更新与传递，其所用环境信息有限，估计精度低且速度慢，而且，这种单节点序贯估计定位方法很容易由于某个节点失效导致整个算法中断，可靠性差。此外，上述算法中各种源参数估计所基于的气体扩散模型均假设符合高斯分布，但实际环境中气体泄漏源的气体扩散是高度非线性的，很难用一个高斯模型来简单代替，因此，其参数估计量的后验概率分布或似然函数很难直接得到。同时，参数估计量在更新与传递过程中所涉及的节点调度和节点间的信息传递均没考虑通信链路能耗或信道噪声的影响。

针对上述单节点序贯估计定位算法存在的问题，本文提出了一种多节点协作的D－MMSE序贯估计气体泄漏源定位算法。主要贡献如下:(1)基于无线传感网络的测量模型，推导了D－MMSE估计量及其均方差的表达式;(2)提出了包含节点间信息增益与通信链路能耗两方面参数的信息融合目标函数，平衡了估计精度与能耗之间矛盾并通过对目标函数寻优实现节点调度选择;(3)引入多个邻居节点信息提高了估计精度和速度，并根据估计量的均方差实时调整邻居节点的数量以达到节能增效目的。仿真结果表明，所提算法在一定能耗前提下可以较高的估计精度和速度实现气体泄漏源定位。

1 气体扩散与观测模型

准确地建立实际监测环境下的气体扩散模型非常困难，但通过湍流扩散理论可以推导相对简单的气体扩散模型［14－15］。本文采用文献［15］中给出的时均气体扩散模型。此模型可描述在时均风速恒定且均匀(Homogeneous)的湍动气流作用下的气体分布状况。假设气体源位于地平面上xs=(xs，ys)处，则气体扩散模型表达式如下:

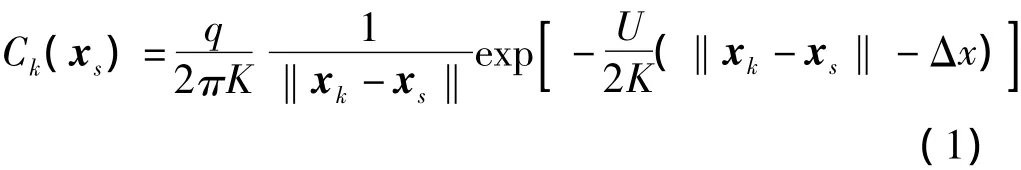
式中，Ck(xs)为区域中坐标为xk=(xk，yk)的传感器节点sk(k=1，2，……n，其中n为网络中传感器节点的总数)处的浓度值;q为气体释放率;K是湍流扩散系数;U为风速值;Δx=(xs－xk)cosφ+(ys－yk) sinφ，φ是x轴正向与上风方向的夹角。

考虑到气体浓度随传播距离增加而衰减的特性，同时参照文献［7］的方法，给出传感器节点sk的观测模型如下:

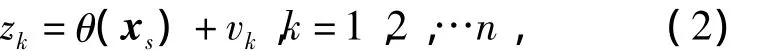
式中，θ(xs)是包含气体源位置信息的随机量，可表示为θ(xs)=λCk(xs)，其中λ是满足均值为μθ、方差为σ2θ的随机变量，vk表示传感器测量噪声，符合均值为零和方差σ2k∝‖xk－xs‖α/2的高斯分布，其中α为气体扩散衰减指数。

2 D-MMSE序贯估计气体泄漏源定位算法

D－MMSE序贯估计实现气体泄漏源定位的核心是构建一个信息融合目标函数，并通过节点间的信息交互，实现气体源位置xs的参数估计。

假设s1为起始节点，根据式(2)可知起始节点的观测值为z1=θ(xs)+v1。定义^θ1为节点s1对θ(xs)的估计量，若^θ1的均方差达不到设定阈值，则^θ1会被传递到下一个节点继续进行融合计算。当k＞1时，节点sk在其自身测量值和第k－1个节点sk－1传递给节点sk的估计值基础上完成估计量的更新，节点sk(k＞1)的观测模型定义如下:

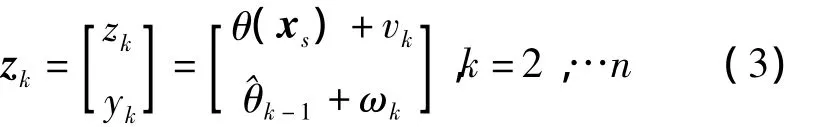
式中，yk为节点sk－1传递给节点sk的含有噪声的信息，θ^k－1为节点sk－1的估计量，ωk为sk－1和sk两个节点之间的信道噪声，符合零均值和方差为∝‖xk－xk－1‖α/2的高斯分布，其中α为气体扩散衰减指数，通常取决于气体源的扩散环境，扩散空间选定为二维时取值为2。

2.1 D-MMSE估计量及其均方差

D－MMSE估计量及其均方差定义如下:

定义1当k=1时，假设参量θ(xs)(后面为描述方便将θ(xs)用θ代替)和观测噪声v1相互独立，基于观测值z1的节点s1获得的MMSE估计量为:

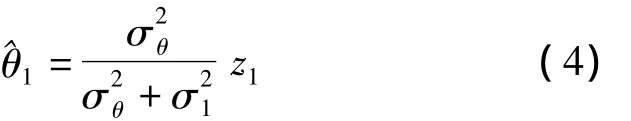
式(4)估计量对应的均方差M1为:

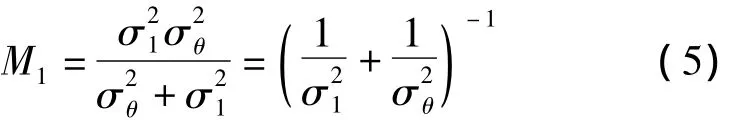
定义2当k＞1时，假设yk和zk服从不同的正态分布且相互独立，分别为:

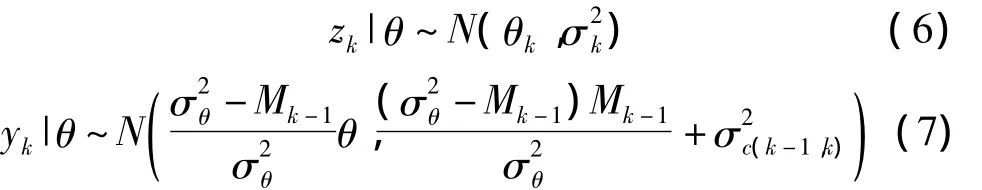
则基于式(3)的观测模型，节点sk的MMSE估计量^θk和对应的均方差Mk分别为:

2.2 信息融合目标函数构造

信息融合目标函数包含节点间信息增益和通信链路能耗两方面参数，其中信息增益参数主要由当前节点和邻居节点的测量值以及气体源的位置信息构成，通信链路能耗则主要包括带宽、延迟等。其定义如下:

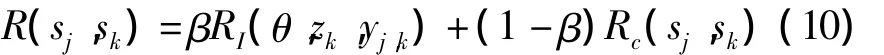
其中:RI(θ，zk，yj，k)表示当前节点sj选择下一节点sk时所产生的信息增益;Rc(sj，sk)表示节点sj和sk之间的通信链路能耗;β∈［0，1］是平衡两个参数项对目标函数影响的系数;yj，k=^θj+nj，k表示当前节点sj传递给下一节点sk的含有噪声的估计结果;nj，k为两个节点之间信道噪声。

节点间信息增益的测算有多种方法［7］，本文基于式(3)气体泄漏源观测模型并运用相对信息熵理论实现信息增益参数测算。当前节点sj选定下一节点sk时产生的信息增益RI(θ，zk，yj，k)可用条件互信息I(θ;zk|yj，k=^θj+nj，k)来表示:

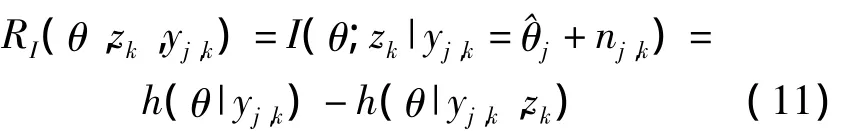
根据式(6)和式(7)描述的yk|θ的概率分布参照文献［16］中的结果可以得出:

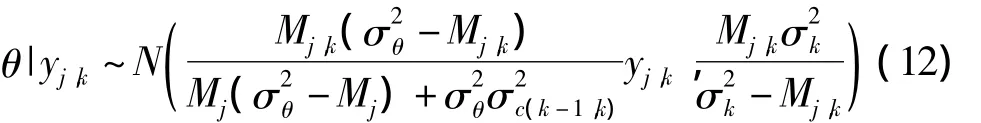
式(11)的第一项可描述为:

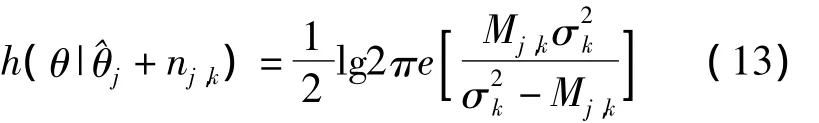
根据式(3)知节点sk的观测量zk符合zk|θ～N(mkθ，Sk)分布，且其均值和方差分别为:

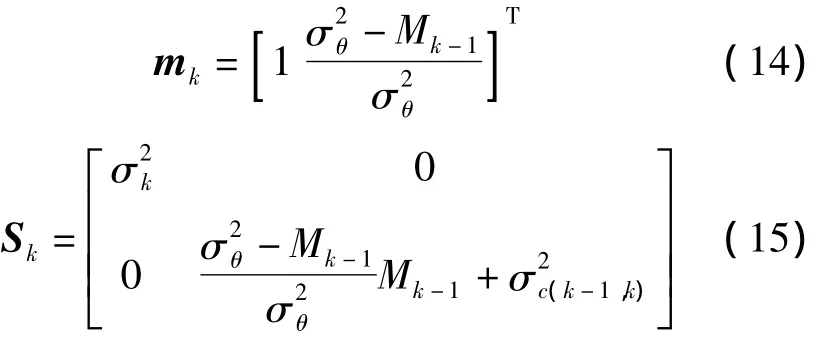
基于文献［16］，则估计量θk后验概率密度函数p(θ|zk)可以定义为:根据MMSE估计定义节点sk对参量θ的MMSE

估计量为:

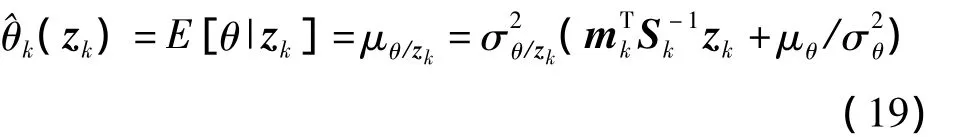
其对应的均方差:

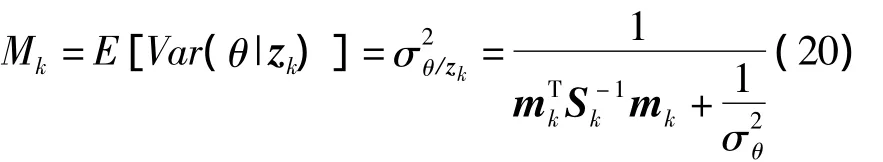
基于式(16)、式(19)和式(20)知:

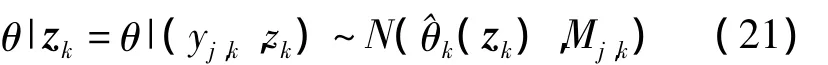
其中Mj，k=E{Var(θ|yj，k，zk}

所以:

由式(13)和式(22)可知:

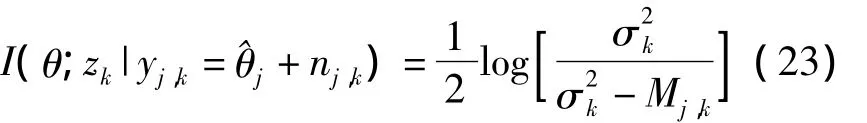
基于条件互信息理论RI(·)可以描述为:

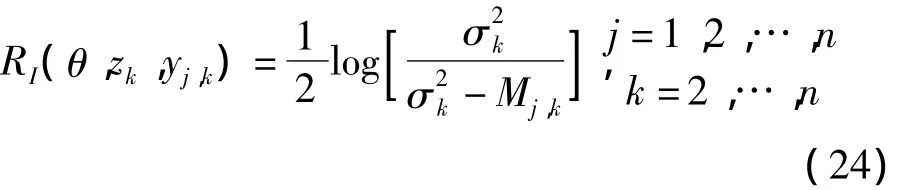
无线传感网络中能量消耗通常包括节点信息采集与处理能耗和节点间信息传输的通信链路能耗，其中通信链路能耗［17－18］占主要部分，节点sj和sk之间的信息交互的通信链路能耗模型为:

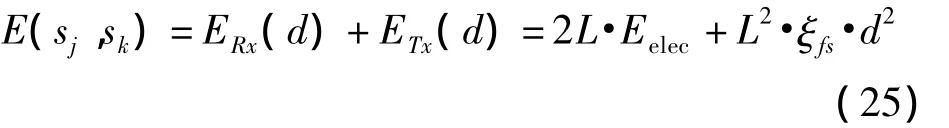
其中ERx表示接收节点所消耗总能量，ETx表示节点传送信息所消耗的总能量，Eelec为传送与接收单位信息元电路消耗的能量且Eelec=50 nJ/bit，ξfs为模型放大器参数，ξfs=10 pJ/bit/m2，L代表信息量(单位bit)常设定为常数。d=(xj－xk)T(xj－xk)为当前节点与候选节点之间距离。

假设d0为预设阈值，通常表示节点的通信半径，则通信链路能耗参数Rc(sj，sk)定义为:

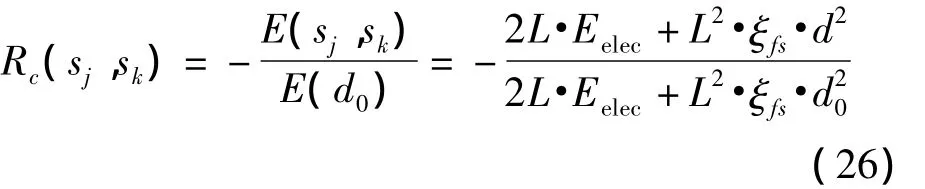
2.3 节点调度算法及其实现

在D－MMSE序贯估计定位算法执行过程中，当前节点只能在有效通信范围内(d≤d0)选择邻居节点并进行信息交互，邻居节点集大小由d0确定，同时，下一个节点的调度也只能在其邻居节点集中通过对式(10)信息融合目标函数寻优实现，算法思想描述如下:

令V={s1，s2，…，sn}表示无线传感网络中所有节点集合，sj∈V为第j周期当前节点，sj+1为第j+1周期要选择的节点。当前节点sj的邻居节点集为以节点sj的位置坐标为圆心半径为d0的圆形区域中的所有节点，定义节点sj的邻居节点集合为Gsj且Gsj⊆V，j=1，2，…，n，即邻居节点集是整个网络节点集的子集。当前节点为sj时，第(j+1)周期调度节点sj+1的选择基于以下公式:

邻居节点集中候选节点的数量对通信链路能耗具有重要影响。假设m={|Gsj|}为第j周期节点sj的侯选节点集Gsj中候选节点sk数目最大值，则m≤n－1，节点sj需要在m个候选节点中选择路由节点，这种情况下，无线传感网络中的n个节点都要参与运算，算法的运算复杂度为O(mn)。当m=n－1时算法的运算复杂度为O(n2)。由式(26)可知减小邻居节点集选择半径d0(即减少邻居节点集中的候选节点数量m)可以减少通信链路能耗，随着m减少，当m≪n－1时算法的运算复杂度可以近似为O(n)，由此可知其能耗将大大降低。因此，本文采用基于估计量均方差动态调整邻居节点集选择半径d0以平衡通信链路能耗与算法估计精度之间关系，达到节能增效的目的。

3 计算机仿真分析

本文在MATLAB平台上对算法的估计性能与影响算法的各种参数间的关系进行了仿真分析并与单节点序贯估计定位算法进行了分析比较。实验区域为100 m×100 m的一个二维空间。假设气体泄漏源真实坐标为(20 m，0)。通过文献［15］中气体物理扩散模型生成相应的浓度数据，其中释放率q选择为80 mL/min，湍流扩散系数K为6m2/s。100个传感器节点随机部署在监测环境区域内，假设已知每个节点sk的坐标位置信息xk=(xk，yk)，k=1，2…，100，在仿真实验中各个节点均可以实时采集并具有时空一致性。考虑到通常所用的金属氧化物半导体气体传感器的相对较长的响应和恢复时间，仿真中节点的浓度采样周期设为5 s，单位为×10－6，即ppm。基于式(3)设定网络中第k个节点的观测噪声和第k个节点和第k－1个节点之间的信道噪声为:

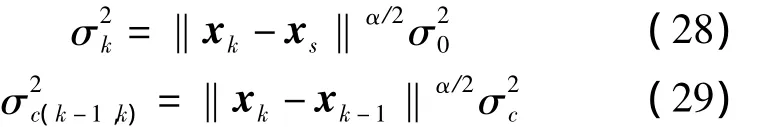
首先，对气泄漏源定位算法中当前节点的邻居节点集选择半径d0与算法估计性能(均方差)及能耗之间的关系分别进行了分析，其中设定α=2，=0.1，=0。

由前面分析可知当前节点的邻居节点集选择半径d0通常决定了其在每个处理周期所选邻居节点的数量，半径越大参与运算的节点数量越多，半径越小则参与运算的节点数量越少。图1给出了不同的选择半径d0=5 m，d0=10 m，d0=15 m，d0=20 m且β=1情况下，定位算法估计性能分析。

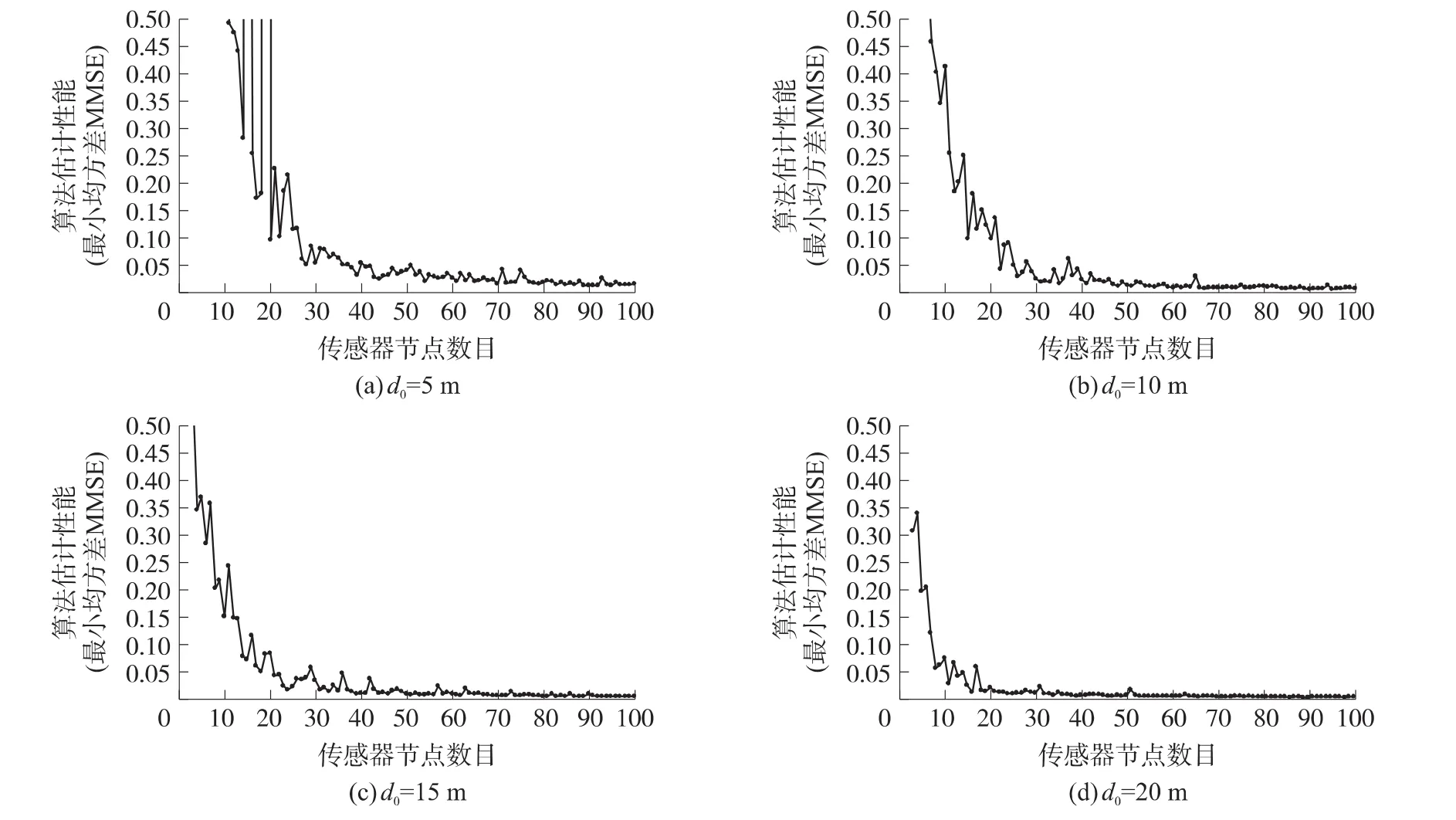
图1 不同邻居节点集选择半径的定位算法估计性能

从图1中可看出，在不同的半径情况下，当传感器运算节点达到一定数量后，气体源的定位精度将不再大范围波动，都趋于收敛，但收敛速度不同，当前节点在不同运算周期，面对不同环境应存在一个最佳的选择半径d0，实时的调整d0可达到经济高效的定位效果。

图2进一步给出了β取不同值时，算法估计性能以及通信链路能耗与邻居节点集的选择半径d0之间关系图，其中通信链路能耗基于式(26)计算，其中设定每次通信息量为L=512 bit。从图2(a)中可以看出d0≤5 m且β≠0时选择半径的变化对算法估计性能影响较大，当d0＞5 m时算法的估计性能(均方差)变化不再明显而是基本趋于平稳。

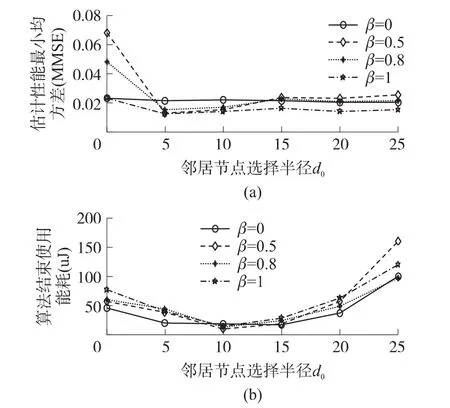
图2 算法估计性能及其能量消耗与邻居节点集选择半径d0关系图

从图2(b)可看出算法结束时其通信链路能耗与邻居节点集选择半径d0并不成正比，这是因为当d0≤5 m时，虽然在每个周期当前节点所选邻居节点数量较少但是其估计误差通常比较大，算法收敛速度慢，参与运算的节点数量会相应增加，整个算法执行过程中所消耗的能量相应也会增加。当d0＞5 m随着选择半径的增加，当前节点的邻居节点数量会增加，算法收敛速度会加快，但由于通讯半径及节点数量的增加其通信链路能耗会双重增加。因此为了降低能量消耗并获得较高的估计性能，需动态调整邻居节点集选择半径以平衡能耗与算法估计性能之间的矛盾。设定邻居节点集选择半径d0与估计性能(均方差)之间的选择规则如下:

(1)当MMSE≤0.03时d0=10 m;

(2)当0.03＜MMSE≤0.08时d0=15 m;

(3)当0.08＜MMSE时d0=20 m。

接下来本文分别对无信道噪声σ2c=0和存在有信道噪声σ2

c=0.001两种情况下定位算法的估计性能进行了分析和比较，其中α=2，σ20=0.1。信息融合目标函数的平衡系数β在(0，1)上间隔0.1递增取值。图3分别给出了两种不同情况下定位算法估计性能与参与运算的节点数目之间的关系。其中上图为无信道噪声的算法性能分析图，下图为存在信道噪声的算法性能分析图。从图3(a)可以看出，当信道噪声σ2

c=0且β取不同值时，算法估计性能会随着参与运算节点数量的增加逐渐趋于收敛，通常可以得到全局MMSE最小值，而图3(b)则表明节点之间通信存在信道噪声σ2c=0.001时，算法的估计性能会随着参与运算节点数量的增加而减小，但超过一定节点以后估计性能反而趋于发散不再收敛。

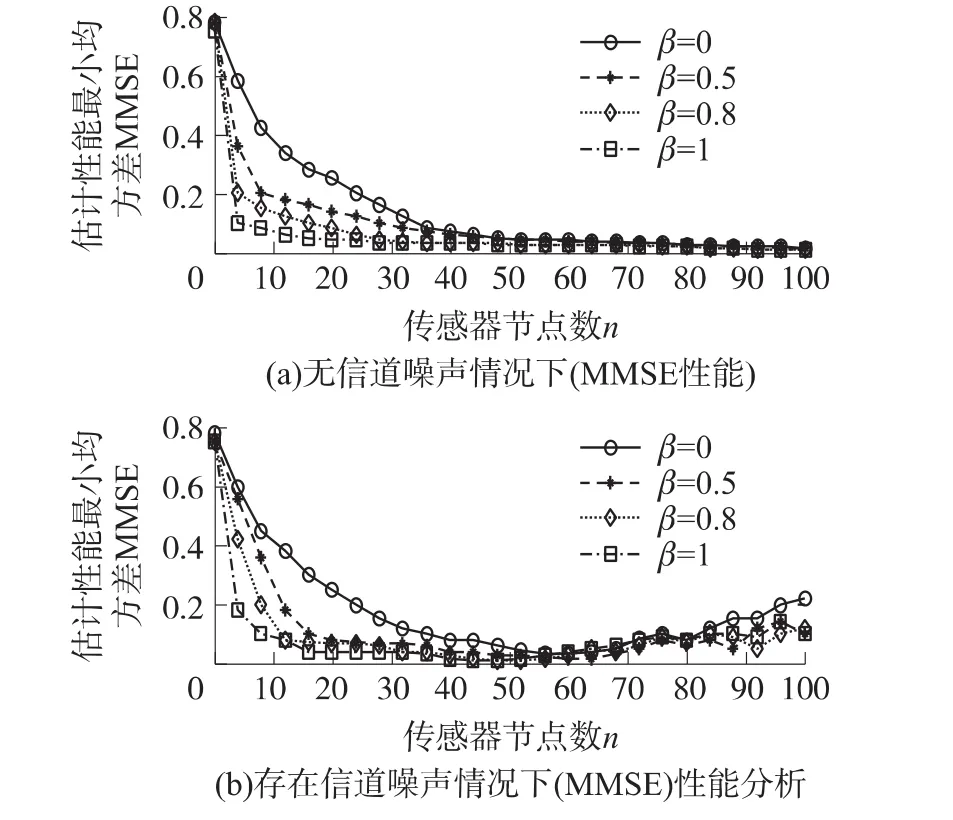
图3 算法估计性能(MMSE)与运算节点关系图

最后，当前节点所选择的邻居节点固定为1时，本文所提的基于多个邻居节点冗余信息的序贯估计定位算法就演变为单节点序贯估计定位算法［8］。

图4对这两种不同气体泄漏源定位算法的性能进行了比较分析，其中α=2，=0.001，β =0.8，设定预估定位阈值2m。从图4中可以看出在初始阶段多节点序贯估计定位算法由于引入邻居节点增加了可用冗余信息其算法的定位误差和收敛速度显然优于单节点序贯估计定位算法，但随着时间增加，单节点定位算法中参与运算的节点数量的增加，两者的估计性能最终将基本趋于一致收敛。同时在初始阶段多节点定位算法所耗能量要高于单节点定位算法，这是因为单个周期内多节点定位算法所调度的邻居节点总数要多于单节点算法。随着多节点定位算法定位误差的降低，其邻居节点集半径将随之调整，以减小所调用的邻居节点数量降低能耗。随着时间增加其能耗将趋于单节点估计算法。

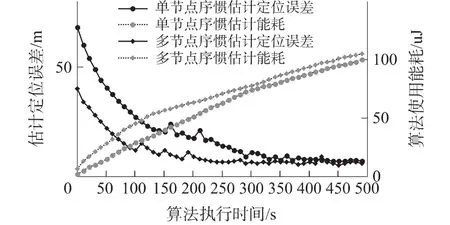
图4 单节点与多节点序贯估计定位算法性能比较图

4 总结

本文基于D－MMSE序贯估计算法实现了无线传感网络中气体泄漏源定位，算法综合考虑了通信链路能耗及估计精度之间的矛盾。时均分布气体扩散模型上的仿真结果表明，所提的D－MMSE序贯估计算法可实现对气体泄漏源的预估定位，对比单节点序贯估计定位算法其在一定能耗条件下可获得较高的定位精度和速度。算法所选邻居节点集的大小影响收敛速度、估计精度和网络能耗:随着邻居节点集半径增大，估计算法的收敛速度加快;当半径增大到一定程度后，估计精度趋于平稳;过大和过小的半径均会导致能耗增大。算法中信息融合目标函数的平衡系数也会影响估计性能:当参与运算的节点数量不多时，平衡系数的取值对算法的估计性能影响更明显。为了节省能耗，通常希望使用尽可能少的传感器节点完成估计，因此选择合适的平衡系数非常重要。接下来将对平衡系数优化选择问题继续深入研究。

［1］Weimer J，Bruce H K，Mitchel J，et al.An Approach to Leak Detection Using Wireless Sensor Networks at Carbon Sequestration Sites［J］.International Journal of Greenhouse Gas Control，2012，9(7): 243－253.

［2］Murvay P S，Silea I.A Survey on Gas Leak Detection and Localization Techniques［J］.Journalof Loss Prevention in the Process Industries，2012，25(6):966－973.

［3］Mitra S，Duttagupta SP，Tuckley D K，etal.3D Ad－Hoc Sensor Networks Based Localization and Risk Assessment of Buried Landfill Gas Source［J］.International Journal of Circuits，System and Signal Processing，2012，6(1):75－86.

［4］Roussel G，Bourgois L，Benjelloun M，et al.Estimation of a Semi－Physical GLBE Model Using Dual EnKF Learning Algorithm Coupled with a Sensor Network Design Strategy:Application to Air Field Monitoring［J］.Information Fusion，2013，14(4):335－348.

［5］Keats A，Yee E，Lien F S.Bayesian Inference for Source Determination with Applications to a Complex Urban Environment［J］.Atmospheric Environment，2007，41(3):465－479.

［6］Ruhi H，Charles J，Ray L，et al.Atmospheric Tomography:a Bayesian Inversion Technique for Determining the Rate and Location of Fugitive Emissions［J］.Environmental Science and Technology，2012，46(3):1739－1746.

［7］Chu M，Haussecker H，Zhao F.Scalable Information－Driven Sensor Querying and Routing for Ad Hoc Heterogeneous Sensor Networks［J］.International Journal of High Performance Computing Applications，2002，16(3):90－110.

［8］牛建军，邓志东，李超.无线传感器网络分布式调度方法研究［J］.自动化学报，2011，37(5):517－528.

［9］周冬鑫，金文光，容志能.基于分层的无线传感网络多跳分簇路由算法［J］.传感技术学报，2011，24(1):73－78.

［10］Zhao T，Nehorai A.Distributed Sequential Bayesian Estimation of a Diffusive Source in Wireless Sensor Networks［J］.IEEE Transactions on Signal Processing，2007，55(4):1511－1524.

［11］Zhao T，Nehorai A.Information－Driven Distributed Maximum Likelihood Estimation Based on Gauss－Newton Method in Wireless Sensor Networks［J］.IEEE Transactions on Signal Processing，2007，55 (9):4669－4682.

［12］Keats A，Yee E，Lien F S.Information Driven Receptor Placement for Contaminant Source Determination［J］.Environmental Modelling and Software，2010，25(9):1000－1013.

［13］Ristic B，Morelande MR，Gunatilaka A.Information Driven Search for Point Sources of Gamma Radiation［J］.Signal Processing，2010， 90(4):1225－1239.

［14］Nehorai A，Porat B，Paldi E.Detection and Localization of Vapor－E－mitting Sources［J］.IEEE Transactions on Signal Processing，1995，43(1):243－253.

［15］Ishida H，Nakamoto T，Moriizumi T.Remote Sensing of Gas/Odor Source Location and Concentration Distribution Using Mobile System［J］.Sensors and Actuators B:Chemical，1998，49(1－2):52－57.

［16］Kay SM，罗鹏飞，张文明，等.统计信号处理基础:估计与检测理论［M］.北京:电子工业出版社，2006:260－264.

［17］邬学军，孟利民，华惊宇，等.基于能量控制的无线传感网络最优化算法研究［J］.传感技术学报，2011，24(3):436－439.

［18］Wang Xingbo，Zhang Huanshui，Fu Minyue.Collaborative Target Tracking in WSNs Using the Combination of Maximum Likelihood Estimation and Kalman Filtering［J］.Journal of Control Theory and Applications，2013，11(1):27－34.

张勇(1978－)，男，博士，讲师，主要研究方向包括无线传感网络，分布式估计，linsio@126.com;

吴玉秀(1984－)，男，博士生，主要研究方向移动传感网络，多机器人主动嗅觉;

孟庆浩(1968－)，男，博士，教授，博士生导师，主要研究方向包括移动机器人导航与控制，机器人主动嗅觉，超声编码研究，qh_meng@tju.edu.cn;

曾明(1973－)，男，博士，副教授，主要研究方向为微操作机器人技术，计算机视觉，数字图像处理。

一种基于分布式最小均方差序贯估计的气体泄漏源定位算法*

张勇1，2，孟庆浩2*，吴玉秀2，曾明2

(1.天津商业大学信息工程学院，天津300134;2.天津大学电气与自动化工程学院，天津300072)

基于无线传感网络的气体泄漏源定位在环境监测、安全防护和污染控制等多个领域具有重要意义。提出一种基于分布式最小均方差(D－MMSE)序贯估计的气体泄漏源定位算法。其通过构建一个包含节点之间信息增益与网络能量消耗两方面参数的信息融合目标函数，并对目标函数寻优实现路由节点的调度与选择。所选节点在其测量值和前节点估计值并通过与邻居节点信息交互的基础上完成气体泄漏源位置参数估计量及其方差的更新与传递。为了降低网络能耗，邻居节点集的选择半径随估计量方差做动态调整。仿真分析表明所提算法对比单节点序贯估计定位算法在一定的能耗条件下可获得较高的定位精度和速度。

无线传感网络;最小均方差;序贯估计;气泄漏源定位

TP393

A

1004－1699(2014)01－0128－07

2013－10－17修改日期:2013－12－04

C:6150P

10.3969/j.issn.1004－1699.2014.01.024

项目来源:国家自然科学基金项目(61271321，60875053，60802051);天津市高校科技发展基金项目(20130710)