Analysis of the Effect of Core Parameters on Input and Output Characteristics of the Fluxgate Sensor*

YANG Shanglin，LIU Shibin，GUO Bo，LIXueliang，QIU Songsong

(School of Electronics and Information，Northwestern Polytechnical University，Xi’an 710129，China)

Analysis of the Effect of Core Parameters on Input and Output Characteristics of the Fluxgate Sensor*

YANG Shanglin，LIU Shibin*，GUO Bo，LIXueliang，QIU Songsong

(School of Electronics and Information，Northwestern Polytechnical University，Xi’an 710129，China)

Aiming at the problem ofwhat parameters of softmagnetic core needed by fluxgate sensor，based on the analysis of themathematicalmodel of fluxgate sensor，it is concluded that under the sine excitation，the optimum excitation magnetic field intensity of the fluxgate sensor istimes the saturated magnetic field intensity of the core.We used hyperbolic tangent function with hysteresis to fit the hysteresis loop of softmagnetic materials，analyzed the influence of saturated magnetic induction intensity，saturated magnetic field intensity，the coercive force，ratio of rectangular and demagnetizing factor on the second harmonic amplitude of induction coils and exciting current of fluxgate sensor，which reveal that the softmagnetic core of high sensitivity magnetic fluxgate sensor should have high permeability and rectangle ratio，low saturationmagnetic field intensity，the coercive force and the demagnetizing factor.The softmagnetic core of low power fluxgate sensor should have high permeability，appropriate rectangle ratio，low saturatedmagnetic induction intensity，saturationmagnetic field intensity，the coercive force and the demagnetizing factor.The comparison of the hysteresis loop of six different cores and their input and output characteristics in the dual core fluxgate，validated the correctness of the conclusions above.

fluxgate sensor;hysteresis loop;softmagnetic core;optimum excitationmagnetic field intensity;secondary harmonic amplitude

对比超导量子干涉仪、霍尔器件、磁阻和磁二极管等其他磁性传感器，磁通门被认为是综合性能最好的矢量磁性传感器［1］，在适当的观测期间分辨率可达到几个pT［2］，在飞机组合导航、潜艇探测、无损探测、卫星定位、交通工具磁罗盘和地磁场变化监测等领域都有应用［3］。

影响磁通门输入输出性能的主要因素有铁芯材料的磁性能、铁芯的形状、激励波形、磁通门类型、磁通门的工作方式、线圈和铁芯的拓扑结构和检测电路等，其中铁芯材料的磁性能无疑是最重要的影响因素。磁通门要求铁芯磁性材料有高的磁导率、低的矫顽力、低的磁致伸缩、低的巴克豪森噪声和低的饱和磁感应强度等［4］。在之前很多人研究不同磁性铁芯对磁通门的影响，其中金惕若［5］根据实际实验来研究这种影响;李菊萍［6］、Dimitropoulos［7］、Perez［8］等利用带矫顽力的三折线磁滞回线模型研究铁芯对磁通门的影响;Ando［9－11］、卢浩［12］、Wang［13］等特别针对RTD磁通门进行了研究;赵东东［14］、Dimitropoulos［15］、Geiler［16］等只是对其中一个参数进行了分析。从这些文献可以看到，有些只是简单说明，没有进行理论分析;有些只是针对个别参数;有些是在简化的三折线磁滞回线模型上进行分析。

本文在前人的基础上，利用反正切函数描述铁芯的磁滞回线，得到了一定频率下磁通门的最佳激励磁场，分析了磁感应强度Bs、饱和磁场强度Hs、矫顽力Hc、剩磁Br和退磁系数N对双铁芯磁通门输出电压二次谐波幅值和激励电流的影响，从而来研究磁通门需要什么样的软磁铁芯的问题。

1 最佳激励电流

1.1 磁通门数学模型

磁通门原理是利用饱和铁芯磁性的非线性特性，使用激励磁场调制外磁场从而检测外磁场。它的一般结构是在一根软磁铁芯上缠绕激励线圈和感应线圈，激励线圈在铁芯上建立的激励磁场为Hex，如果激励磁场强度为:

其中Hm为激励磁场强度幅值，f为激励电源频率。设铁芯的横截面积为S，磁导率为μ(t)，感应线圈的匝数为N2，由于铁芯磁化曲线的非线性，激励磁场的瞬时值变化也会引起磁导率μ(t)的变化。根据法拉第电磁感应定律，感应线圈上应产生的感应电动势为:

由于激励磁场瞬时值方向周期性变化，而随之而变的铁芯磁导率μ(t)为无正负之分，文献［17］认为μ(t)为偶函数。本文认为由于矫顽力的存在，这种偶次性得到了一定的影响，但影响较小，将μ(t)认为是偶函数仍能使后面的分析有效和简化。将μ(t)展开为傅里叶级数，可得:

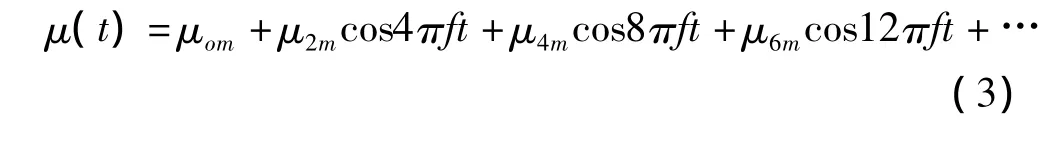
在考虑实际中环境磁场施加在铁芯轴向的分量H0时，双铁芯磁通门次级输出电压可表示为式(4).双铁芯磁通门的构造如图1所示。

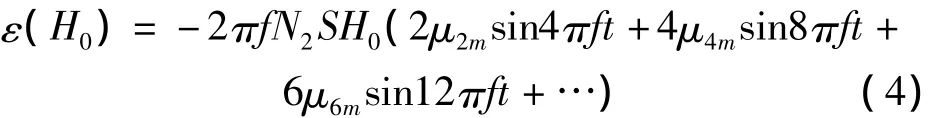
其中根据周期偶函数的傅里叶级数的公式可得:

图1 双铁芯磁通门

从式(4)我们可以看到，影响次级电压输出的因素包括:激励频率f、感应线圈匝数N2、铁芯的横截面积S、环境磁场H0和铁芯磁导率μ(t)的傅里叶展开级数系数μ2m、μ4m、μ6m等，而这些级数系数是与铁芯的磁滞回线形状有密切关系的。

1.2 磁滞回线模型

因为软磁铁芯磁滞回线呈现出的“S”形状，这里我们用双曲正切函数和反正切函数来拟合铁芯磁滞回线数据，结果如图2所示。其中原始数据用点来表示，反正切函数用较粗的点划线表示，双曲正切函数拟合用较细的小线段表示。前期工作告诉我们用这些“S”形函数拟合磁滞回线，对磁通门的分析是有效的［18］。拟合结果表明相对反正切函数［19］，在描述高磁导率的磁滞回线时，双曲正切函数拟合的均方根误差(RMSE)为0.010 80，比反正切函数的0.013 08小。故在这里我们用双曲正切函数拟合具有高磁导率的磁通门软磁铁芯。

图2 磁滞回线拟合对比图

1.3 二次谐波的选择和最佳激励电流确定

根据厂家给出的1J85铁芯磁滞回线的参数，即饱和磁场强度Hs=12.812 A/m、Hc=0.96 A/m、Br=0.274 2 T和Bs=0.75 T，我们用双曲正切函数拟合磁滞回线参数，得到磁滞回线的表达式如式(8)。

若用激励磁场H=Hm·cost来激励磁通门，根据式(5)所示，此处μ2m可表示为:由于磁滞的存在，磁滞回线上升阶段的磁导率表示为μu(t)，下降阶段的磁导率表示为μd(t)，这样傅里叶级数二次系数μ2m可利用图3中来理解，其中为了使被积函数μm(t)·cos(2t)和μd(t)·cos(2t)达到最大，应使cos(2t)为负时μu(t)、μd(t)大于0，cos(2t)为正时μu(t)、μd(t)等于0。即要使μ2m达到最大值，则要使cos(2t)为正值的时候，铁芯达到饱和状态，此时激励磁场要大于等于饱和磁场强度，即Hmcos(t)≥Hs，所以激励磁场应满足下式(11)～式(13)。本文认为矫顽力Hc不影响磁滞回线的饱和点，即不影响μ2m最大值的确定。设ω=2πf。

图3 μ2m计算和最佳激励磁场确定

同理，根据图4和图5可以确定μ4m和μ6m取最大值的条件和激励磁场大小。要使μ4m达到最大，则≥Hs，即Hm≥2.613 1Hs。同样，要使μ6m达到最大，则，即Hm≥3.863 7Hs。从功耗的角度来说，我们选择μ2m将会使激励磁场降低，功耗降低。这里参照文献［20］，将最佳激励磁场Hm0定义为:在正弦磁场激励下，使磁通门测量线圈输出电压二次谐波幅值取得最大值时的激励磁场幅值。根据这个定义磁通门的最佳激励磁场为:

其中Hs为实际铁芯的饱和磁场强度值，受铁芯的退磁效应影响。式(14)的结果与文献［20］中的结果一致。

图4 μ4m计算和最佳激励磁场确定

图5 μ6m计算和最佳激励磁场确定

2 磁滞回线参数对输出二次谐波和激励电流的影响

2.1 磁滞回线参数对输出二次谐波的影响

根据式(8)～式(10)，通过分别改变饱和磁感应强度Bs、饱和磁场强度Hs、矫顽力Hc、矩形比Br/Bs和退磁系数N，在零外磁场H0条件下(负反馈情况)，拟合出新的磁滞回线表达式，从而计算出磁导率的表达式和μ2m的大小。仿真中所选取的参数变化点都是在有效范围内均匀取值，具有一般性，可以反映μ2m随参数变化趋势。式(10)是个定积分的式子，我们通过复化求积公式来计算它的数值。

2.1.1 变化饱和磁感应强度Bs

分别取大小是原始饱和磁感应强度Bs的0.5、0.75、1、1.5和2倍的Bs，其他参变量不变，来拟合出新的磁滞回线，得到的μ2m随Bs变化的情况如图6所示。从图6(a)可以看出随着饱和磁感应强度Bs的增大，μ2m基本上是线性增加的。从式(8)、式(9)可以知道这样定义下随着磁导率μ的增加，傅里叶级数二次系数μ2m也同样是线性增加的，这与要求高磁导率软磁材料是吻合的。

2.1.2 变化饱和磁场强度Hs

分别取大小是原始饱和磁场强度Hs大小的0.2、0.3、0.4、0.5、0.75、1、1.5和2倍的Hs，其他参变量不变，来拟合出新的磁滞回线，得到的μ2m随Hs变化的情况如图6(b)所示。从图6(b)可以看出随着饱和磁场强度Hs的增大，傅里叶级数二次系数μ2m呈指数地减小;在磁场强度Hs增加一定程度，μ2m不再减小。

2.1.3 变化矫顽力Hc

分别取大小是原始矫顽力Hc0.2、0.5、0.75、1、1.5和2倍的Hc，其他参变量不变，来拟合出新的磁滞回线，得到的μ2m随Hc变化的情况如图6(c)所示。从图6(c)可以看出，随着矫顽力Hc的增加，傅里叶级数二次系数μ2m呈抛物线地减小。

2.1.4 变化矩形比Br/Bs

分别取大小是原始矩形比Br/Bs0.1、0.2、0.365 6、0.7和0.9倍的Br/Bs，其他参变量不变，来拟合出新的磁滞回线，得到的μ2m随Br/Bs变化的情况如图6(d)所示。从图6(d)可以看出，随着变化矩形比Br/Bs的增加，傅里叶级数二次系数μ2m呈对数地增加，增加速度再逐渐缩小。

图6 随磁滞回线参数变化图

2.1.5 变化退磁系数N

分别取退磁系数N大小为10－3、2.5×10－4、10－4、2.5×10－5、10－5、2.5×10－6和10－6，其他参变量不变，来拟合出新的磁滞回线，得到的μ2m随N变化的情况如图7所示。如图7所示，随着退磁系数N对数地增大，傅里叶级数二次系数μ2m呈指数地减小，而且相对其他因素，μ2m的数值变化较大。

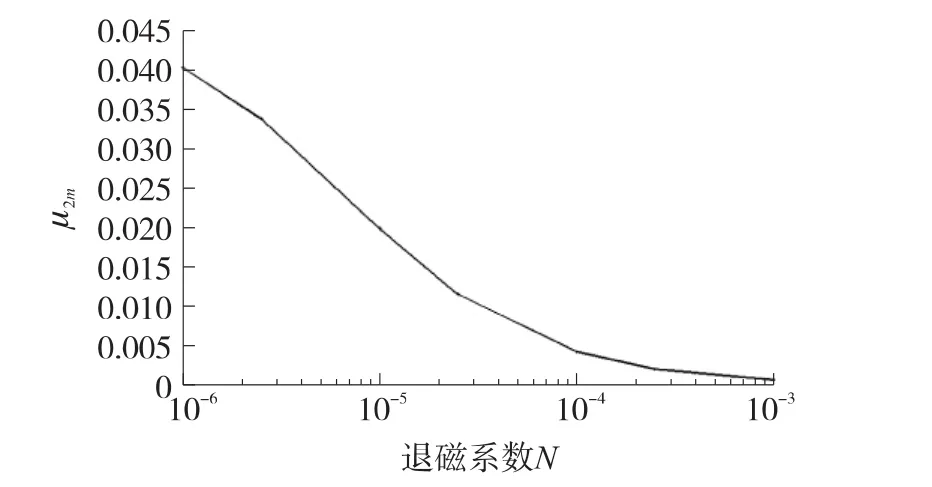
图7 随退磁系数N变化图

2.2 磁滞回线参数对激励电流的影响

2.2.1 磁滞回线参数对激励电流的影响

2.2.2 退磁系数N对激励电流的影响

因为软磁材料μr≫1，所以式(15)可变为

积分可得

分别取退磁系数N为10－3、10－4、10－5和10－6，得到新的磁滞回线如图8所示。

图8中实线是铁芯材料磁滞回线，虚线是退磁场影响下的铁芯有效磁滞回线。可以看出退磁系数N对饱和磁场强度Hs影响较大，当退磁系数N增大时，相应饱和磁场强度也增大，即激励电流增大。所以在设计铁芯拓扑结构是应尽量减小退磁系数N，使磁路闭合或是适当减小横截面积和磁导率。

图8 退磁系数N对铁芯磁滞回线的影响

3 实验验证

3.1 相同退磁系数材料对比

本文分别用在3种不同条件下电镀的镍铁合金薄膜作为双铁芯磁通门铁芯，测试它们的磁滞回线、双铁芯磁通门输出二次谐波幅值和激励电流。3种薄膜铁芯的尺度都是30 mm×1 mm×4μm，它们的退磁系数相同，从而可以来验证在相同退磁系数下材料其他参数的影响。用自制的磁滞回线测量设备，在1 kHz的激励磁场下测量得3种铁芯的磁滞回线分别如图9～图11所示。从图中可以读出和计算出3种铁芯磁滞回线的参数如表1所示。从图9～图11和表1中，我们可以看到，3种电镀镍铁薄膜铁芯的饱和磁感应强度Bs基本一致，薄膜铁芯B的饱和磁场强度Hs和矫顽力Hc在3种铁芯中都是最小的，只有矩形比略比铁芯A要小。铁芯C的饱和磁场强度Hs和矫顽力Hc都是最大的，矩形比是3种铁芯中最小的。从前面仿真分析的结果，可以预测铁芯B的综合性能应该是最好的。

图9 电镀镍铁薄膜铁芯A磁滞回线

图10 电镀镍铁薄膜铁芯B磁滞回线

图11 电镀镍铁薄膜铁芯C磁滞回线

表1 不同电镀镍铁薄膜铁芯磁滞回线参数

在外磁场为50μT，在频率是1 kHz正弦电压激励下，测试如图1所示结构的双铁芯磁通门，分别检测输入电流峰值的有效值和输出电压的二次谐波幅值，结果如表2所示。我们可以看出薄膜铁芯B的二次谐波幅值是3种铁芯中最大，激励电流有效值是最小的，是3种铁芯中性能最适合磁通门的。这与我们之前的仿真分析是一致的。但同时我们看到铁芯C的激励电流有效值比铁芯A的小，这是因为铁芯A有更大的矩形比，在饱和磁感应强度Bs和矫顽力Hc差不多的情况下，导致铁芯的磁滞损耗变大，则需要更大的激励电流，这与文献［4］中的结论一致，这也说明高矩形比带来的损耗是不能忽视的。

表2 不同铁芯磁通门输入输出性能

3.2 不同退磁系数材料对比

因为退磁系数也是本文考察的参数之一，本文分别用磁通门中最常用的1J85带材、钴基非晶带材和电镀镍铁薄膜这3种不同尺寸铁芯作为双铁芯磁通门铁芯(3种铁芯的尺寸如下表3)，测试它们的磁滞回线、双铁芯磁通门二次谐波幅值和激励电流，从而来验证前面的分析。用自制的磁滞回线测量设备，在1 kHz的激励磁场下测量得3种铁芯的磁滞回线分别如图12～图14所示。从图中可以读出和计算出3种铁芯磁滞回线的参数如表4所示。从图12～图14和表4中可以看出，带材的矫顽力比电镀薄膜的小很多，但因为退磁的影响，带材的磁导率变小，饱和磁场强度变大。

表3 不同铁芯参数

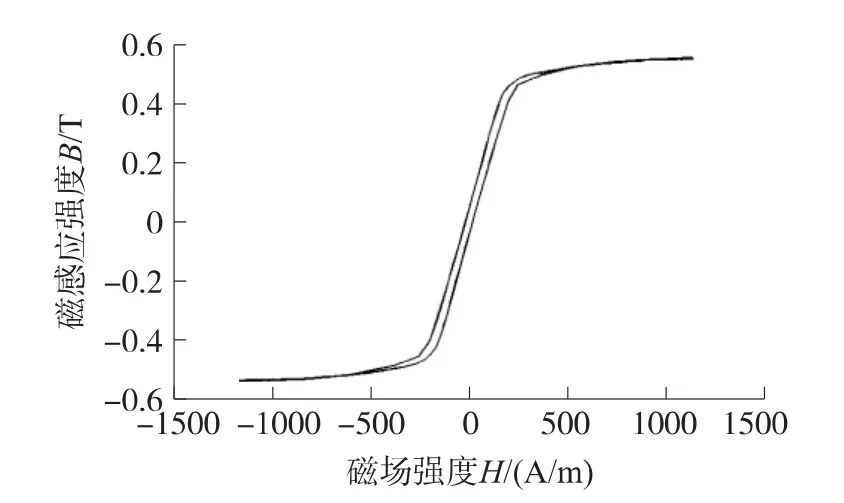
图12 1J85磁滞回线

图13 钴基非晶磁滞回线

图14 电镀铁镍合金磁滞回线

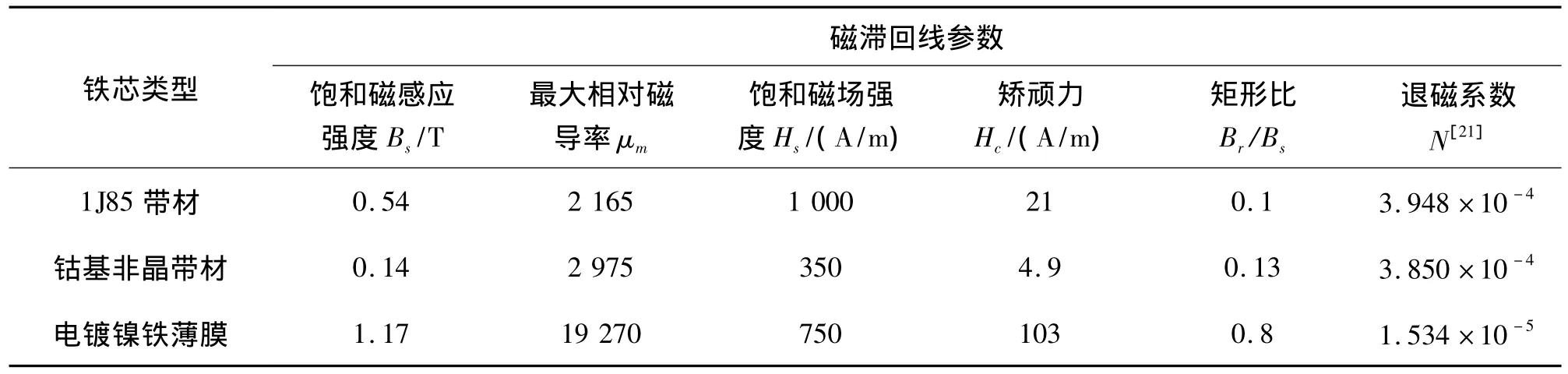
表4 不同铁芯磁滞回线参数

在外磁场为50，在频率是1 kHz正弦电压激励下，测试如图1所示结构的双铁芯磁通门，分别检测输入电流峰值的有效值和输出电压的二次谐波幅值。根据式(4)，在激励频率、次级线圈以及外磁场一样的情况下，为了比较铁芯的性能，我们又计算了二次谐波幅值/铁芯截面积的大小，如表5所示。从表5我们可以看出，1J85的二次谐波幅值最大，但其二次谐波幅值/铁芯截面积不是最大的，这主要因为1J85带材相对其他两种材料厚度较厚;同时因为它的饱和磁场强度较大和厚度较大导致退磁系数较大，使得激励电流有效值很大。钴基非晶带材因为较低的饱和磁场强度，使得它的激励电流有效值最小，同时较小的矫顽力和饱和磁感应强度使得它适合用于低功耗磁通门。电镀镍铁合金因为其厚度很小，导致较低的退磁系数和较大的矩形比和二次谐波幅值/铁芯截面积，因此这种铁芯适合做高灵敏度的磁通门应用，但其截面积较小，输出电压较低，还应考虑其噪声问题，才能在弱磁场检测时得到应用。

表5 不同铁芯磁通门输入输出性能

4 结论

从上面的理论分析和实验验证中可以得到以下结论:

(1)在正弦磁场激励下，使磁通门测量线圈输出电压二次谐波幅值取得最大值时的激励磁场幅值应为实际铁芯饱和磁场强度的倍，而且矫顽力不会影响这个关系。选择输出电压二次谐波也是使激励最小的必然选择。

(2)为了增大二次谐波的幅值，应选择磁导率高、饱和磁场强度小、矫顽力小、矩形比大和退磁系数小的一定形状铁芯材料。

(3)为了减小激励电流大小，应选择饱和磁感应强度小、饱和磁场强度小、矫顽力小、一定矩形比和退磁系数小的一定形状铁芯材料。

(4)综合结论(2)和(3)考虑，既要得到较大的二次谐波输出又要降低激励电流，应选择磁导率高、饱和磁感应强度小、饱和磁场强度小、矫顽力小和适当矩形比和退磁系数小的一定形状铁芯材料。在这些参数中退磁系数的影响最大，设计铁芯拓扑结构时尽量使磁路闭合;在一些开磁路铁芯中，可适当降低铁芯磁导率和矩形比，或是采用层叠铁芯来降低单个铁芯的横截面积，从而降低退磁系数、涡流和噪声。采用初次级变铁芯横截面积结构降低激励电流时，可以采用不同的铁芯材料组合，初级可以选择饱和磁场强度小的的材料，次级可以选择饱和磁感应强度小的铁芯。

［1］Ripka P，Janosek M.Advances in Magnetic Field Sensors［J］. IEEE Sens J，2010，10(6):1108－1116.

［2］Ando B，Baglio S，Bulsara A R，et al.Design and Characterization of a Microwire Fluxgate Magnetometer［J］.Sens Actuator APhys，2009，151(2):145－153.

［3］Deak JG，Koch R H，Guthmiller G E，etal.Dynamic Calculation of the Responsivity of Monodomain Fluxgate Magnetometers［J］. IEEE Trans Magn，2000，36(4):2052－2056.

［4］Ripka P.Magnetic Sensorsand Magnetometers［M］.Boston:Artech House，2001.88.

［5］金惕若.磁通门探头磁心的测试［J］.电测与仪表，1998，35 (5):18－21.

［6］李菊萍，刘诗斌，郭博，等.基于四次谐波选择法的磁通门传感器分析［J］.传感技术学报，2011，24(10):1412－1415.

［7］Dimitropoulos P D，Avaritsiotis J N，Hristoforou E.Boosting the Performance of Miniature Fluxgates with Novel Signal Extraction Techniques［J］.Sens Actuator A－Phys，2001，90(1－2):56－72.

［8］Perez L，Lucas I，Aroca C，et al.Analytical Model for the Sensitivity of a Toroidal Fluxgate sensor［J］.Sensors and Actuators，A: Physical，2006，130－131(SPEC.ISS.):142－146.

［9］Ando B，Baglio S，Bulsara A，et al.Effects of Driving Mode on RTD－FluxGate Performances［C］//Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference，IMTC/ 04，May 18，2004－May 20，2004.Como，Italy:Institute of Electrical and Electronics Engineers Inc.，2004.1419－1423.

［10］Ando B，Baglio S，Bulsara A R，et al.Investigate the Optimal Geometry to Minimize the Demagnetizing Effect in RTD－Fluxgate［C］//IMTC’06—IEEE Instrumentation and Measurement Technology Conference，April 24，2006－April 27，2006.Sorrento，Italy:Institute of Electrical and Electronics Engineers Inc.，2006. 2175－2178.

［11］Ando B，Baglio S，Sacco V，et al.Investigation on Optimal Materials Selection in RTD－Fluxgate Design［C］//IMTC’05—Proceedings of the IEEE Instrumentation and Measurement Technology Conference，May 16，2005－May 19，2005.Ottawa，ON，Canada: Institute of Electrical and Electronics Engineers Inc.，2005.1261－1265.

［12］卢浩，程德福，王言章，等.动态磁导率的反正切模型研究及其在时间差型磁通门的应用［J］.传感技术学报，2012，25(9): 1226－1229.

［13］Wang Y，Wu S，Zhou Z，etal.Research on the Dynamic Hysteresis Loop Model of the Residence Times Difference(RTD)－Fluxgate［J］.Sensors(Switzerland)，2013，13(9):11539－11552.

［14］赵东东，刘斯，曹大平.环形坡莫合金磁心的磁化曲线函数构造与应用［J］.磁性材料及器件，2012，43(6):24－28.

［15］Dimitropoulos P D.Noise Sources in Miniature Fluxgate Sensors Part I:Theoretical Treatment［J］.Int J Electron，2005，92(9): 499－524.

［16］Geiler A L，Harris V G，Vittoria C，et al.A Quantitative Model for the Nonlinear Response of Fluxgate Magnetometers［J］.J Appl Phys，2006，99(8):08B316－1－08b316－3.

［17］张学孚，陆怡良.磁通门技术［M］.北京:国防工业出版社，1995:2.

［18］Yang S，Liu S，Feng W，et al.SPICE Circuit Model of Voltage Excitation Fluxgate Sensor［J］.IET Science，Measurement and Technology，2013，7(3):145－150.

［19］罗巍，刘诗斌.磁通门中的坡莫合金材料的磁滞回线的拟合［J］.金属功能材料，2008，15(6):30－32.

［20］刘诗斌.微型智能磁航向系统研究［D］.西安:西北工业大学，2001.

［21］Chen D X，Pardo E，Sanchez A.Demagnetizing Factors for Rectangular Prisms［J］.Magnetics，IEEE Transactions on，2005，41(6): 2077－2088.

杨尚林(1983－)，男，宁夏灵武人，西北工业大学电子信息学院博士研究生。专业方向为微电子与固体电子学，现在主要从事微型磁通门传感器研究，ysl029@163.com;

刘诗斌(1960－)，男，河南巩义市人，西北工业大学电子信息学院教授，博士生导师。长期从事无人机传感器系统研究工作，研究领域为磁场和压力测量，智能传感器系统，微电子和计算机应用，liushibin@nwpu.edu.cn。

铁芯参数对磁通门输入输出特性影响分析*

杨尚林，刘诗斌*，郭博，李学亮，秋颂松

(西北工业大学电子信息学院，西安710129)

针对磁通门需要什么参数的软磁铁芯的问题，在分析磁通门数学模型基础上，得出了正弦激励条件下磁通门的最佳激励磁场为铁芯饱和磁场强度的倍;以带磁滞的双曲正切函数拟合软磁材料磁滞回线，分析了饱和磁感应强度、饱和磁场强度、矫顽力、矩形比和退磁系数对输出二次谐波幅值和激励电流的影响，得出高灵敏度磁通门铁芯应具有高磁导率和矩形比，低饱和磁场强度、矫顽力和退磁系数;低功耗磁通门铁芯应具有高磁导率，适当的矩形比，低饱和磁感应强度、饱和磁场强度、矫顽力和退磁系数;最后通过对比两组六种不同铁芯的磁滞回线和双铁芯磁通门输入输出特性，验证了以上结论的正确性。

磁通门传感器;磁滞回线;软磁铁芯;最佳激励磁场;二次谐波幅值

TP212.1

A

1004－1699(2014)01－0040－08

2013－11－12修改日期:2013－12－31

C:7310L;3120D

10.3969/j.issn.1004－1699.2014.01.008

项目来源:国家自然科学基金项目(60874101);高等学校博士学科点专项科研基金项目(20126102110031);西北工业大学研究生创业种子基金项目(Z2013074，Z2013075)