Analysis of the Harmonic Frequency to Piezoelectric Ceramic Embedded in Concrete*

LIU Li，CHEN Yu，XU Zhilong，WANGQin，ZHAO Airong

(School Of Electronics And Information Engineering，Sichuan University，Chengdu 610065，China)

Analysis of the Harmonic Frequency to Piezoelectric Ceramic Embedded in Concrete*

LIU Li，CHEN Yu*，XU Zhilong，WANGQin，ZHAO Airong

(School Of Electronics And Information Engineering，Sichuan University，Chengdu 610065，China)

A research about the vibrationmode of piezoelectric ceramic(PZT－5H)based on ANSYShas beenmade，combiningwith harmonic response algorithm to obtain three different regions of vibration－frequency curve of piezoelectric ceramic，realizing the simulation of acoustic pressure cloud picture of the electronic－acoustic system with embedded type of piezoelectric concretemodule while coupling piezoelectric ceramic and concrete units，and further receiving themaximum acoustic pressure and acoustic fields distribution under different excitation frequency.The results shows that the piezoelectric ceramic has fourmaximum amplitude points in 20 kHz～100 kHz.Alongwith the increase of harmonic frequency，and the increase of amplitude，the vibration distribution takes on the variation trend of scattering before concentration;through the analysis of harmonic response，it shows that different regions of piezoelectric ceramic acoustic radiant surface all has themaximum vibration－frequency nearby 80 kHz;according to the analysis of acoustic fields of electronic－acoustic system，if the excitation frequency is79.666 kHz，the acoustic pressure is themaximum，the acoustic fields is the best and the acoustic directivity is concentrated.

concrete;piezoelectric ceramic;harmonic frequency;electronic－to－acoustic system

现代建筑行业中，对成品混凝土内部有可能出现的裂缝、空洞等缺陷进行无损检测，实时掌握这些缺陷的发展规律，预测混凝土后期的耐久性和承载性，有利于排除安全隐患，对实现安全生产起到至关重要的作用［1］。在混凝土结构的健康检测中，无损超声检测是主要方法［2－3］。文玉梅等将压电材料埋入混凝土内部，提出一种压电埋入式混凝土无损超声检测的方法［4－5］。压电埋入式混凝土无损检测是一种由电信号激励压电材料进行电－声转换来获取混凝土内部信息的技术，实现结构的在线、不间断、主动及无源检测。陈雨等通过制作压电埋入式机敏模块，研究了埋入混凝土中压电陶瓷温度及应力特性［6－8］。压电材料埋入混凝土内部，会产生一些如辐射声场能量弱、压电陶瓷激励效率低、换能器接收信号微弱等问题［9］。此外，混凝土健康检测过程中的超声激励、压电陶瓷声场辐射、换能器信号接收均会产生噪声，干扰有用信号，影响检测结果，因此要实现混凝土的在线实时监测，应加强埋入混凝土中压电陶瓷的声辐射效应，提高声激励效率，提高系统信噪比，减小混凝土内部结构信息的估测误差，从而提高混凝土在线监测的有效性和实用性。

对于提高埋入式压电陶瓷电－声系统的声激励响应研究已有一些成果，文献［10］在压电陶瓷一侧层合金属背衬，以不同激励频率激励压电陶瓷进行声能分析，找到了一种提高压电陶瓷声激励效率的方法;文献［11］通过构造小波改进阈值函数，对压电传感器的输出信号进行降噪，达到了提高系统信噪比的目的。本文基于物理学中共振［12］会使压电陶瓷电－声系统的振动强度达到最大、辐射产生的声能量达到最高的原理，对压电陶瓷进行了振动模态分析，得出共振情形下的多个谐振频率点，通过谐响应分析压电陶瓷声辐射面的不同区域，得出压电陶瓷中心点、中心区域、边缘区域应变－频率曲线，验证了模态分析得出的结论，通过分析比较找到了压电陶瓷的最优谐振频率点。通过在ANSYS中选择相应单元，模拟了压电埋入式混凝土机敏模块的研究模型，并以最优谐振频率同频的电信号来激励压电陶瓷，实现了埋入混凝土中压电陶瓷电－声系统的声压云图仿真，得到不同激励频率下的最大声压和声场分布情况，并再次验证了以最优谐振频率79.666 kHz激励埋入式压电陶瓷产生最佳谐振振动的结论。

1 压电陶瓷谐振频率点的分析

1.1 埋入混凝土中压电陶瓷电－声系统设计

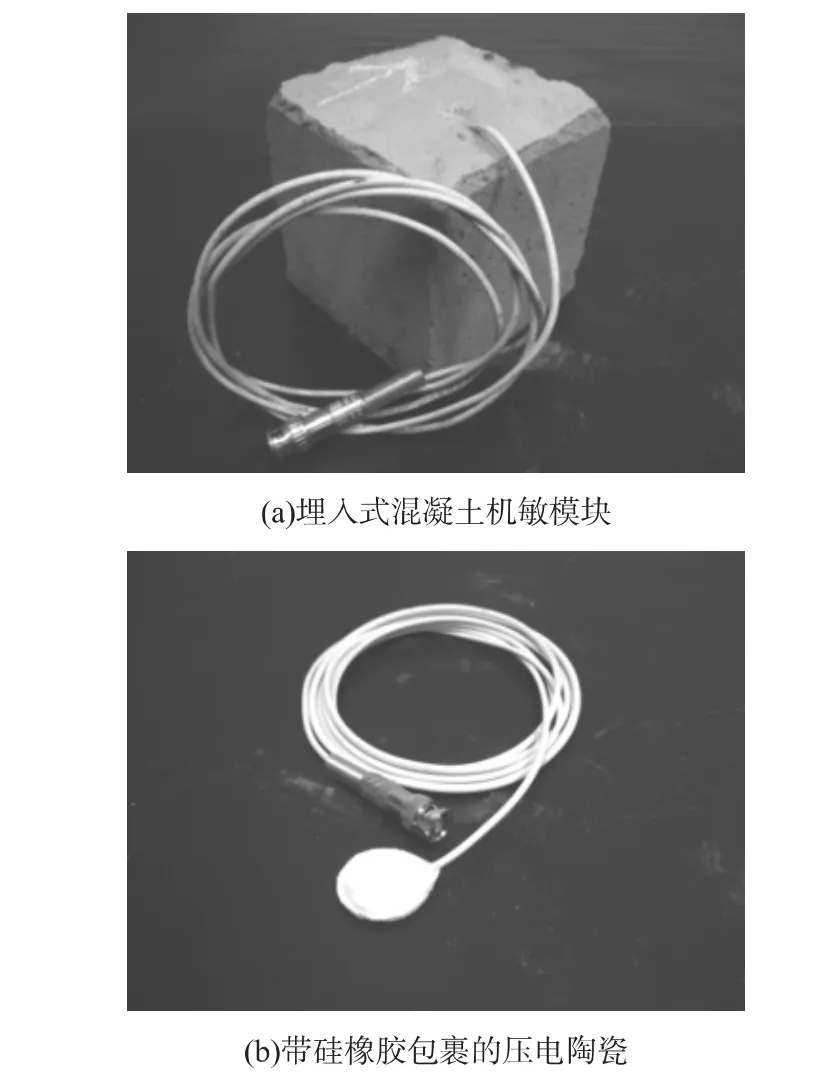
图1 埋入式混凝土机敏模块与带硅橡胶包裹的压电陶瓷图

压电陶瓷(PZT－5H铌镁锆钛酸铅三元系压电陶瓷)［13］是一种具有电声效应的电声材料，将压电陶瓷埋入待浇筑的混凝土，制作成机敏模块，如图1(a)所示。该模块可以对混凝土结构实现在线实时检测，当以压电陶瓷谐振频率同频的周期脉冲激励机敏模块中的压电陶瓷时，压电陶瓷可产生谐振振动，出现较强的振动状态而有利应用于待测结构厚、信号干扰强的混凝土类型。因为混凝土早期浇筑过程的凝固和干缩而引起非均匀体积变化从而造成对检测效果的影响，而压电陶瓷本身比较脆，可使用硅橡胶覆盖于压电陶瓷表面，不仅可以避免因混凝土浇筑过程中的干缩力对其产生的损伤，而且可以增加压电陶瓷的声阻抗匹配。此外硅橡胶还具有绝缘、防腐蚀的特性，可以起到保护压电陶瓷的作用，将同轴电缆接于压电陶瓷上下两个表面，尾部制作成激励输入口，实验模型如图1(b)所示。

埋入混凝土中压电陶瓷电－声系统的设计是利用压电陶瓷具有逆压电效应，通过激励电信号埋入混凝土的压电陶瓷，由压电换能器接收辐射产生的声信号，经过声－电转化导入示波器中实现对声波传播路径上所携带的混凝土内部信息的获取。如图2所示，超声换能器在另一侧进行声波接收，再转化成电信号导入示波器进行波形调节和显示，也可将传递出的信息拷贝入PC内进行后期信号降噪、信号谱分析等等，对携带的有用信号进行进一步处理，以提高分析的准确性。

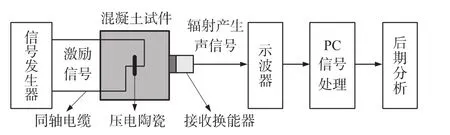
图2 基于压电埋入式混凝土机敏结构的无损检测电－声系统

1.2 基于简正运动下的压电陶瓷分析

针对使用压电陶瓷材料制作而成的PZT－5H电声器件而言，压电振子可以看作一块板状结构。所选用的压电陶瓷圆片半径为12 mm，厚度为2 mm，径向距离相比厚度而言较小且材料中相应的波长相比也较小，所以PZT－5H压电陶瓷可近似看作一个“薄”的平板。

根据文献［14］中振动方程:

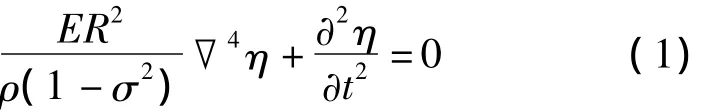
方程中E为杨氏模量，R为圆片的半径，ρ为密度，σ为泊松比，η(t，x，y)表示圆片中心面上任何一点在垂直方向的位移，▽4是直角坐标的一种算符，再根据分离变量法可求出压电陶瓷振动的简正频率为

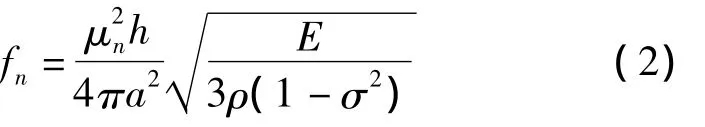
PZT－5H压电陶瓷厚度h=2 mm，压电圆片的钳定直径为a=24 mm，弹性常数矩阵由文献［15］可得，再根据压电陶瓷的参数，求出了第1泛频、第2泛频、第3泛频、第4泛频如表1所示。

表1 PZT－5H压电陶瓷的简正频率

简正运动是无阻尼运动，虽然一个系统的简正运动所对应的简正频率反映了系统的固有频率特性，但是本文的研究模型是将压电陶瓷(PZT－5H)埋入混凝土内部，制作成压电埋入式混凝土机敏模块，会因为凝固过程中的干缩力、混凝土夹层对压电陶瓷产生夹持力等阻尼效应，与简正振动模式存在条件不符的问题。结合已有研究结果［10，16］发现表1的计算结果与压电陶瓷的谐振频率存在绝对误差，不能根据简正模式下的压电陶瓷来得出结论，所以本文基于ANSYS软件，从模态仿真入手分析压电陶瓷振动模态，得出与压电埋入环境相符的谐振频率分布情况和最优谐振频率。

1.3 压电陶瓷PZT－5H模态分析

为了确定压电陶瓷在不同振动模态下与其固有频率的对应关系，对PZT－5H进行模态分析［17］发现在20 kHz～100 kHz频段内有14个不同的振动模态，各阶模态下其振幅、谐振频率均不同。如图3所示，在二维坐标系中将14种振动模态的振幅－频率进行描点，得到了振幅－频率变化折线。

图3 PZT－5H振幅－频率变化折线

图3 中20 kHz～100 kHz频段内压电陶瓷的振幅出现了4个极大值，分别对应4个谐振频率点: 40.307 kHz、60.928 kHz、79.666 kHz、84.895 kHz，描点于图4所示，4个振幅极大值点对应的振幅随着频率增加而增加。图5分别对图4中谐振频率点所对应的振动模态进行提取，图中压电陶瓷分布的不同颜色对应颜色轴，可知机械振动在声辐射表面产生了不同大小的应变分布。

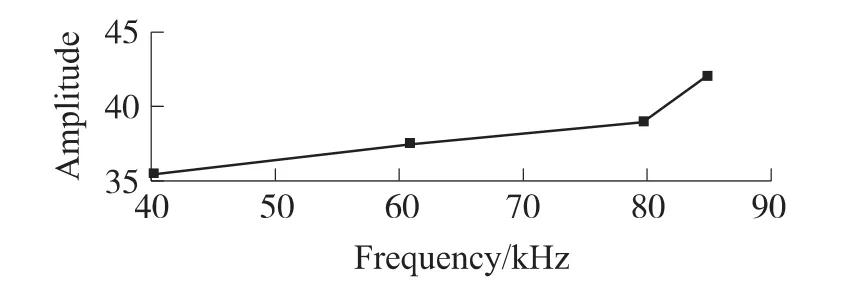
图4 PZT－5H振幅极大值－频率变化折线

图5 不同谐振频率点所对应的谐振模态图

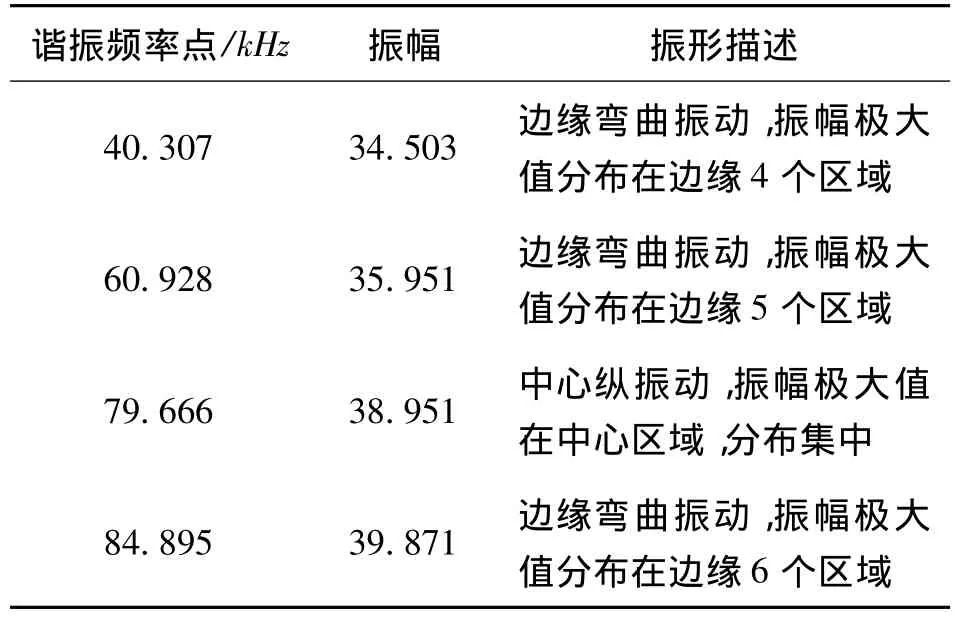
表2 PZT－5H在20 kHz～100 kHz的谐振频率和振形描述

PZT－5H压电陶瓷进行模态分析，在20 kHz～100 kHz频段内压电陶瓷有14个不同的振动模态，特对其中4个振幅极大值所在的频率点进行模态分析。由图可知压电陶瓷声辐射面存在不同的振幅极值区，随着谐振频率的增加，振幅逐渐增加，而振动分布呈先集中后分散的变化趋势，且图5(a)、5(b)、5(d)是边缘厚度振动，图5(c)为中心振动，振动幅度最大值出现在中心点处，且振动分布均匀，圆片中心到边缘区域应力强度顺次递减到边缘区域边界再继续进行反方向递增，为典型的中心区域振动模型;图5(a)、5(b)、5(d)中，振动明显地带为边缘区域并以正弦波动形状振动，中心区域振动幅度不大，应力值较小，边缘区域分别为4、5、6个振幅极大值，并以边界最强振动衰弱到两侧，为边缘振动模型。由图中可知，4个谐振频率点中只有图5(c)为中心振动，即为在谐振频率点79.666 kHz处可产生能量最强最集中的振动。

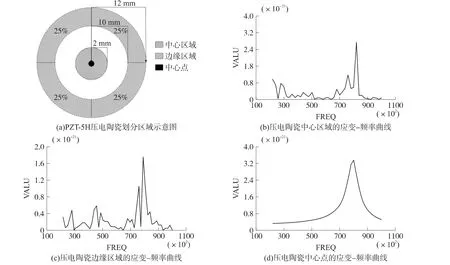
图6 压电陶瓷划分区域图及中心应变的频率曲线图

模态分析得到了压电陶瓷在20 kHz～100 kHz频率内各阶振动模态和谐振频率点，通过分析比较得出较优谐振频率点为79.666 kHz，由于压电陶瓷表面不同区域振动下谐振点的分布情况不明确，所以需要进行谐响应分析，一方面来验证本节结论，另一方面找出压电陶瓷不同区域下谐振频率与相应振幅的关系。

1.4 压电陶瓷PZT－5H谐响应分析

压电陶瓷为高耦合、高介电常数、高柔顺性锆钛酸铅压电陶瓷PZT－5H，沿厚度方向极化。将压电陶瓷划分为3个区域(如图6(a))，使用POST26在压电陶瓷电压自由度耦合部中选取节点序号最低的节点，提取其沿厚度方向的应变值，通过截取3个具有代表性的地方(边缘区域、中心区域、中心点)进行频率－应变曲线图的求解。

由图6(b)、6(c)、6(d)和表3可知，图6(b)为边缘区域的应变－频率曲线，图中出现多个振幅极值点，多个谐振频率点，而最优谐振频率点出现在82.125 kHz，振幅最大值为2.76×10－21，达到了此区域中最强的振动状态;图6(c)为中心区域出现多个振幅极值点，多个谐振频率点，而最优谐振频率点出现在79.666 kHz，振动幅度为1.75×10－21;图6 (d)为中心点处谐振频率点80.000 kHz，振动幅度为3.30×10－8。从图6(b)、6(c)、6(d)中，中心处(中心区域和中心点处)的最优谐振频率点都在80 kHz附近，最大振幅出现在中心点处且远大于中心区域和边缘区域，可见中心点处激励产生的振动状态最强。分析不同区域的最优谐振频点，取三者的平均值近似为80.597 kHz，与1.3节中模态分析得出的结论相差不大。综上可知压电陶瓷声辐射面上的不同区域产生的最大应变时谐振频率均在80 kHz附近，即使用80 kHz同频的电信号激励埋入混凝土中的压电陶瓷时可达较强的振动强度，产生较大的振动幅度。

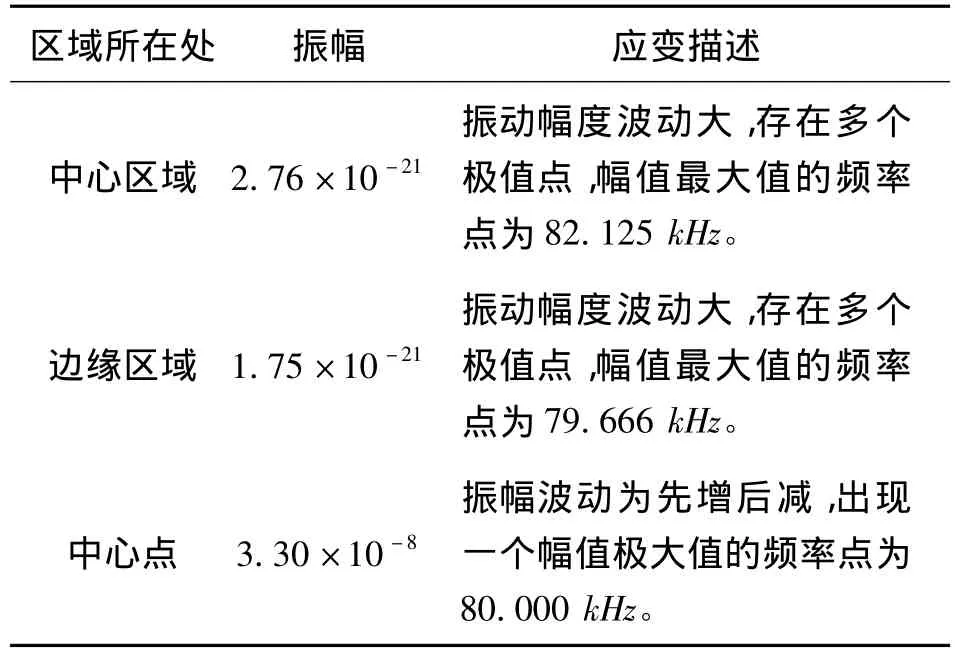
表3 PZT－5H声辐射面不同区域的应变描述

2 压电陶瓷PZT－5H声场分析

由于压电陶瓷通过振动向外辐射声波，所以应变和声场之间必然存在某种联系［18］。在声场理论与激励频率关系中，压电陶瓷受激励频率作用辐射声波响应不仅与振动幅度也与声指向性相关。下面将进行声场仿真来模拟压电陶瓷埋入混凝土中的声辐射效应。通过3节的结论可知，若以约80 kHz的频率作为压电陶瓷的激励频率，进行压电埋入式混凝土机敏模块的声辐射实验，推断应可达到声指向性集中、声压较大的声场效果。

压电陶瓷在20 kHz～100 kHz频段内有4个谐振频率点，实验分别选择这4个频点作为激励频率来仿真产生最大振幅时的声场分布情况。由于压电陶瓷的振动状态与机电耦合相关，所以对压电陶瓷建模时选用具有耦合属性的SOLID5单元，后用PLANE223单元，混凝土环境则因为具有各向异性的材质性能，无法利用有限元工具进行准确的应力分布仿真，基于此考虑，选择与混凝土密度、声传播速度相同的其他材质代替实现模拟混凝土对压电陶瓷进行包裹。图7为压电陶瓷声场仿真模型，有限元分析中网格划分完毕后的图形。通过声场仿真，获得压电陶瓷辐射超声波的声压云图，也叫声波速图，所测声压值由不同的颜色来表示，单位是帕斯卡(Pa)。

图7 压电陶瓷声场仿真模型的网格划分图

从表4中验证了压电陶瓷的主要振动方式为厚度方向振动，但是也有一定的径向振动，也可以看出声场呈对称分布，径向和厚度方向均会辐射声场，随着激励频率越大，径向声场辐射范围:40.307 kHz较小，60.928 kHz、79.666 kHz、84.895 kHz基本相同，均是小范围辐射声场;厚度方向声场辐射范围:40.307 kHz较小，60.928 kHz、79.666 kHz、84.895 kHz呈递增趋势，但是发现以79.666 kHz为电信号的激励频率时，声场分布最集中，辐射产生的超声信号最强，能够使混凝土外侧的压电换能器更好地接收超声信号。结合声压云图分析可知79.666 kHz频点处激励埋入式压电陶瓷辐射超声波的声振动幅度最大、声压值最大，声指向性最集中，则可产生的声辐射能量最大，应用于压电埋入式混凝土无损检测优势明显。

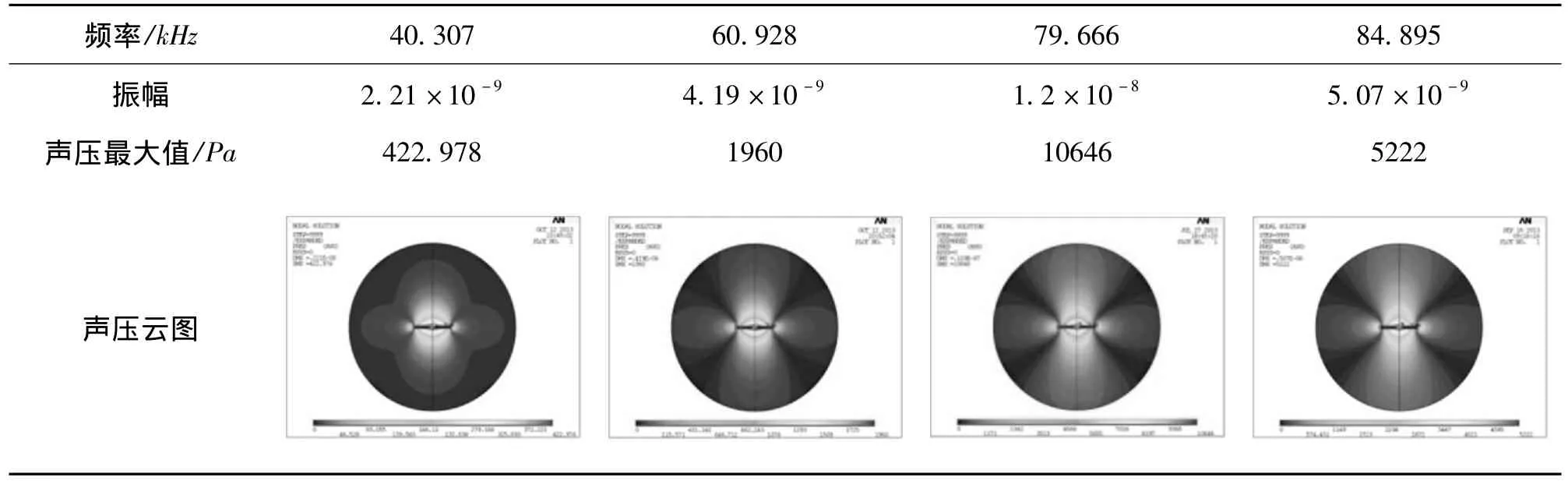
表4 压电陶瓷PZT－5H辐射超声波的声压云图

3 结论

文中建立了埋入混凝土中压电陶瓷电－声系统的研究模型，通过理论分析压电陶瓷的简正频率，并结合ANSYS对PZT－5H压电陶瓷进行模态分析、谐响应分析、声压云图仿真，得出并验证了PZT－5H在多种振动情况下的较优谐振频率点为79.666 kHz。通过有限元分析发现，利用信号发生器发射电信号激励埋入混凝土中的压电陶瓷，当激励频率选择较优谐振频率79.666 kHz时，辐射声能量较强、声场较集中，激励而产生的振动强度也较大，可在压电埋入式混凝土健康检测实验中获取更准确的结构信息。若采用压电陶瓷的较优谐振频率点来进行激励，可得到较优的声波辐射图，以便后期进行混凝土结构的波形分析，为后期实现更理想的混凝土健康检测结果打下理论基础。

［1］李为杜.混凝土无损检测技术［M］.同济大学出版社，1989.9.

［2］吴慧敏.结构混凝土现场检测新技术——混凝土非破损检测［M］.湖南:湖南大学出版社，1998.7.

［3］朱建林，向礼丹，柳莎莎，等.超声波传感器在混凝土无损检测系统中的应用研究［J］.传感技术学报，2008，21(7)，1－5.

［4］Wen Y，Li P，Huang S.Study on the Readout of Piezoelectric Distributed Sensing Network Embedded in Concrete［J］.SPIE，1998 (3):64－67.

［5］文玉梅，李平，刘双临，等.压电机敏混凝土原理［J］.压电与声光，2002(6):196－198.

［6］陈雨，文玉梅，李平.压电陶瓷应力作用下的损失特性［J］.仪器仪表学报，2004，25(增刊):151－153.

［7］陈雨，文玉梅，李平.埋入混凝土中压电陶瓷应力及温度特性研究［J］.应用力学报，2006，23(4):658－661.

［8］陈雨，文玉梅，李平.利用埋入式压电陶瓷进行混凝土结构应力监测的实验研究［C］//第九届全国敏感元件与传感器学术会议.北京:国防工业出版社，2005.

［9］Pickett G.Effect of Aggregate on Shrinkage of Concrete and a Hypothesis Concerning Shrinkage［J］.ACI Journal Proceedings，1956，52(1):581－590.

［10］谭斌，陈雨，李鹏程，等.厚度振动模式下背衬结构PZT的声能特性［J］.应用力学学报，2012，29(1):32－37.

［11］汪琴，陈雨，谭斌，等.基于提升小波的压电传感器输出信号的改进阈值降噪［J］.应用力学学报，2013，30(4):1－5.

［12］邵建华，顾柏平.物理学［M］.上海:上海科学技术出版社，2013.1.

［13］张福学.现代压电学［M］北京:科学出版社，2001.9.

［14］朱哲民，龚秀芬，杜功焕.声学基础［M］.南京:南京大学出版社，2001.3.

［15］王荣津.水声材料手册［M］.北京:科学出版社，1983.7.

［16］李鹏程，陈雨，谭斌，等.背衬对埋入混凝土中压电陶瓷电－声特性的影响［J］.传感技术学报，2012，25(1):44－48.

［17］尚晓江，赵海峰.ANSYS结构有限元高级分析方法与范例应用［M］.北京:中国水利水电出版社，2006.1.

［18］黄润，陈雨，李鹏程，等.埋入混凝土中压电陶瓷圆片声指向性和能量的研究［J］.传感技术学报，2011，24(9):1270－1274.

刘丽(1989－)，女，四川崇州人，四川大学硕士研究生，主要研究方向为信号与信息处理、结构健康检测，liuliddup @126.com;

陈雨(1976－)，男，1999年获重庆大学动力工程学院电厂专业学士学位，2002年获重庆大学动力工程学院动力机械及系统专业硕士学位，2006年获重庆大学光电工程学院仪器科学与技术专业博士学位，2006～2009年在重庆大学任教，2009年至今工作于四川大学电子信息学院，副教授职称。主要研究方向为:结构健康监测、混凝土压电机敏结构、压电传感器，ychen@scu.edu.cn。

基于ANSYS的埋入混凝土中压电陶瓷谐振频率分析*

刘丽，陈雨*，徐志龙，汪琴，赵爱荣
(四川大学电子信息学院，成都610065)

基于ANSYS研究压电陶瓷(PZT－5H)的振动模态，结合谐响应算法得出压电陶瓷3个不同区域的应变－频率曲线，并将压电陶瓷和混凝土单元耦合，实现了压电埋入式混凝土机敏模块的电－声系统声压云图仿真，得到了不同激励频率下的最大声压和声场分布。结果表明压电陶瓷在20 kHz～100 kHz频段内有4个振幅极大值频率点，随着谐振频率的增加，振幅逐渐增加，而振动分布呈先集中后分散的变化趋势;通过谐响应分析发现压电陶瓷声辐射面不同区域最大应变频率均在80 kHz附近;由电－声系统的声场分析发现压电陶瓷的激励频率为79.666 kHz时声压最大、声场分布最优、声指向性集中。

压电陶瓷;混凝土;谐振频率;电－声系统

O482.41

A

1004－1699(2014)01－0084－06

2013－11－10修改日期:2013－12－16

C:2860;7810C

10.3969/j.issn.1004－1699.2014.01.016

项目来源:国家自然科学基金项目(61174025);国家自然科学青年基金项目(50808186);重庆市自然科学基金项目(CSTC，2008BB0155)