基于迭代UKF的主动段弹道跟踪算法研究＊

孙 雷，李 冬，易东云

（1.国防科学技术大学理学院，湖南 长沙410073；2.南京炮兵学院，江苏 南京211132）

1 引言

卫星主要采用星载红外传感器，通过被动探测，获得弹道导弹的到达角信息，实现对目标发射的监视、跟踪、弹道估计等功能［1，2］。弹道导弹的飞行过程分为主动段和被动段，主动段包括垂直上升段、转弯段、过渡段和稳定段。红外传感器只能获取导弹目标的到达角和辐射强度信息，观测情形如图1所示。

卫星在只有角度测量信息下对于弹道导弹主动段的跟踪属于无源跟踪，导弹目标的状态方程和测量方程都是非线性的，并且卫星与目标距离较远，可观测性较弱。这些都对主动段弹道跟踪问题带来了较大的困难，因此寻找一种快速收敛且具有较高精度的跟踪算法十分关键。

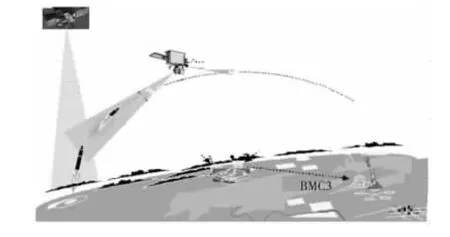
Figure 1 Obervation of the trajectory form the satellite图1 卫星对导弹主动段的观测

扩展卡尔曼滤波 EKF（Extended Kalman Fil－ter）是常用的非线性滤波算法，但在实际应用中它存在明显的缺陷。无迹卡尔曼滤波 UKF（Unscented Kalman Filter）是目前受到广泛使用的非线性滤波算法，通过选取一些样点更精确地给出状态变量经过非线性变化后的均值和方差，减小了线性化带来的误差，避免了EKF算法在求解Jacobi矩阵带来的Fisher矩阵病态问题。但是，标准的UKF算法存在收敛速度慢、精度不高的问题。一种易于实现的提高非线性近似精度的方式是使用迭代测量更新的方式，这在EKF上已经得到了成功的应用［3］。与迭代EKF的思想类似，可以使用状态的估计值代替预测值来重新进行无迹变换UT（Unscented Transformation），得到新的滤波参数，并再次利用观测值来改善估计状态，从而提高状态估计的精度，已有文献提出迭代UKF的思想和易于实现的迭代测量更新的UKF算法［4，5］。

本文通过分析弹道导弹在主动段的受力情况，引入一种基于重力转弯模型的状态方程。根据基于迭代测量更新的UKF思想，研究其在卫星观测信息下的迭代更新过程，从而建立基于迭代UKF的主动段跟踪算法。仿真结果表明，迭代UKF算法与标准UKF算法相比，收敛速度更快、跟踪精度更好，是一种适应性更强的导弹目标主动段跟踪算法。

2 主动段弹道估计模型

主动段为弹道导弹飞行的第一个阶段，其强机动特性和变质量过程使得主动段弹道动力学特性十分复杂。主动段时间并不长，一般在几十秒到几百秒范围内，但是主动段的跟踪对于被动段的状态估计以及导弹的射程和落点却起着决定性作用。

对主动段弹道准确地建模是实现弹道导弹跟踪的前提，主动段的跟踪模型分为导弹的主动段状态模型和预警卫星观测模型。

2.1 主动段弹道模型

导弹在主动段的受力情况十分复杂，主要包括推力、重力、气动阻力等。对用于主动段弹道估计的目标状态方程已有相关的研究［6，7］，其中一种为基于重力转弯假设的状态方程。重力转弯假设是指假设导弹在主动段飞行过程中，攻角很小，几乎为零，推力与阻力均沿速度方向，重力是使弹道弯曲的唯一因素，因此称为重力转弯。本文使用的目标状态方程就是重力转弯模型。

设导弹在地心惯性坐标系ECI（Earth Cen－tered Intertial）下的位置速度矢量分别为r和v，则r＝ ［x y z］T，v＝˙r＝ ［˙x ˙y ˙z］T。导弹受到的力可以分为沿重力方向的力和沿速度方向的力，在重力转弯假设条件下，导弹弹道参数的主动段动力学方程可记为：

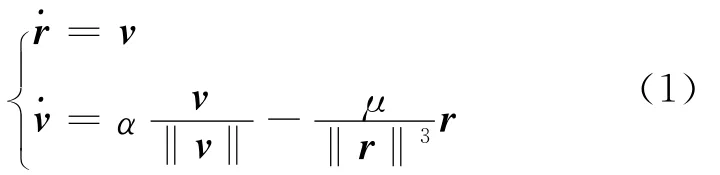
其中，μ为地球引力常数，α为导弹推力加速度大小。考虑实际中大气透过率的影响，红外传感器在导弹飞出稠密大气层后才能发现目标，因此这里忽略气动加速度的影响。

下面分析推力加速度大小α随时间变化的情况。设导弹推力大小为常值T，则推力加速度可以写成：

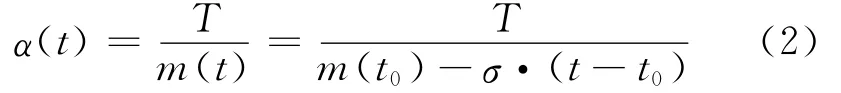
其中，m（t）为t时刻导弹的瞬时质量，σ为发动机秒耗量，t0为初始时刻。

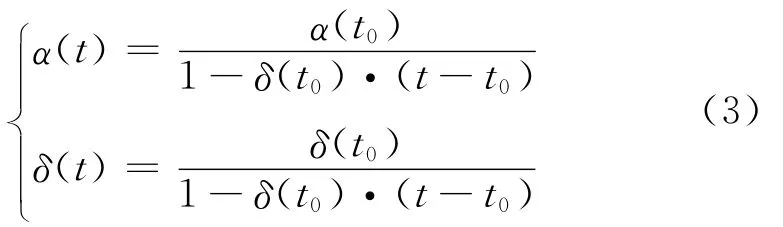
上式对时间求导后可以得到：

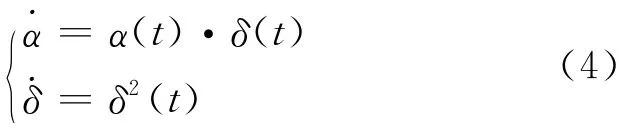
结合公式（1）和公式（4），就可以得到基于重力转弯模型的主动段状态方程：

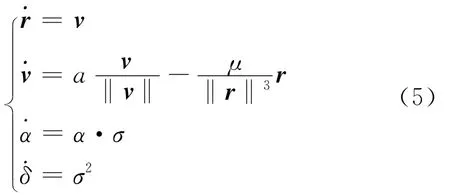
目 标 的 状 态 记 为：X ＝ ［x，y，z，˙x，˙y，˙z，α，∑］T，则主动段动力学模型（5）可以表示为：

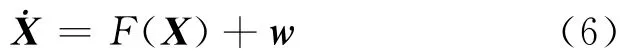
其中，X为目标的状态，w为零均值不相关的状态噪声。根据给定的初始条件，采用数值积分的方法对公式（6）求解就可以得到导弹在主动段某一时刻的位置和速度。

2.2 卫星角度观测方程

在卫星测量坐标系 UEN（Up East North）中，角测量方程定义如下：

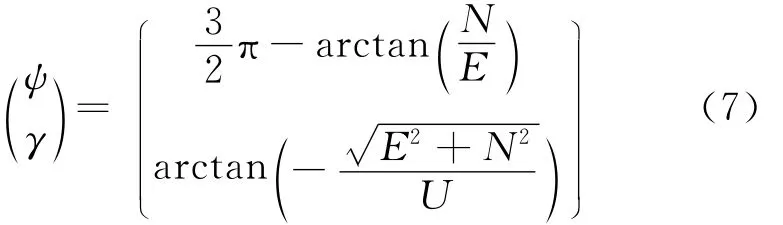
其中，ψ和γ分别是目标在UEN坐标系下的方位角和俯仰角，如图2所示。

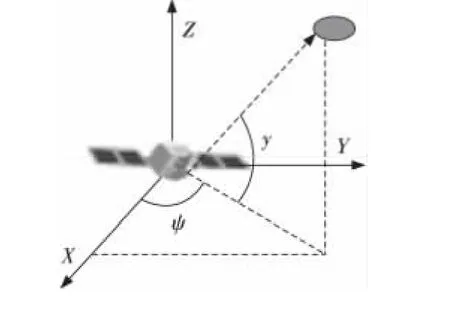
Figure 2 Satellite observation model图2 卫星观测模型

观测模型基于目标的角度测量信息，设在Tk时刻目标在ECI坐标系下的状态变量为Xk，其中位置变量为rk，卫星的位置变量记为sk，根据ECI坐标系与UEN坐标系的关系，Tk时刻卫星的视线测量矢量zk可以表示为：

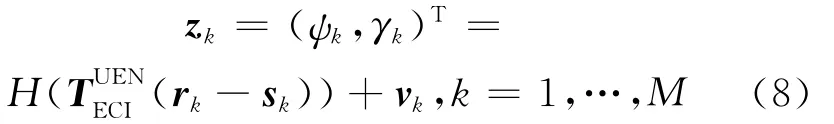
3 迭代UKF滤波算法

UKF算法是基于UT变换和Kalman滤波技术的一种滤波算法［8，9］，其通过特别选取一些样点，更好地近似随机变量经过非线性变化后的均值和方差。将系统围绕状态估计重新进行UT变换计算滤波参数，然后再一次利用观测值改善对状态的估计，这就是迭代 UKF——IUKF（Iterated UKF）的思想。

3.1 UT变换

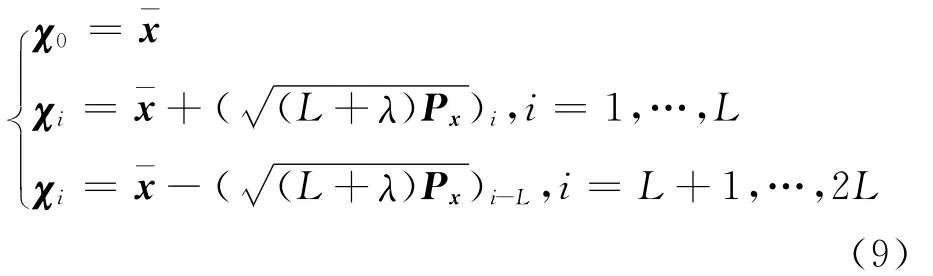
UT变换是一种计算随机变量在经历非线性变换后的统计特性的方法。考虑一个随机变量x（维数为L），通过一个非线性函数y＝f（x）得到随机变量y，假设x具有均值¯x与协方差Px，为计算y的统计特性，首先根据下式：得到2L＋1个Sigma采样点，其中λ＝φ2（L＋κ）－L为尺度参数，常数φ决定这些Sigma采样点在x¯附近的扩展范围；κ是另一个尺度因子，通常取为0或3－L；（是矩阵方根的第i列，矩阵方根可以通过Cholesky分解得到。将Sigma采样点代入非线性函数：

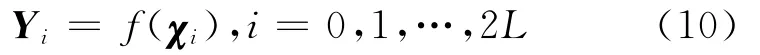
通过下式计算y的均值和协方差矩阵：

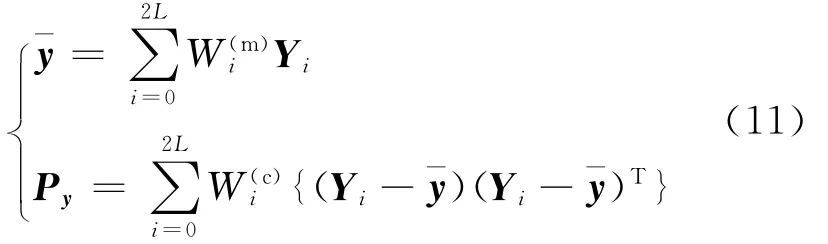
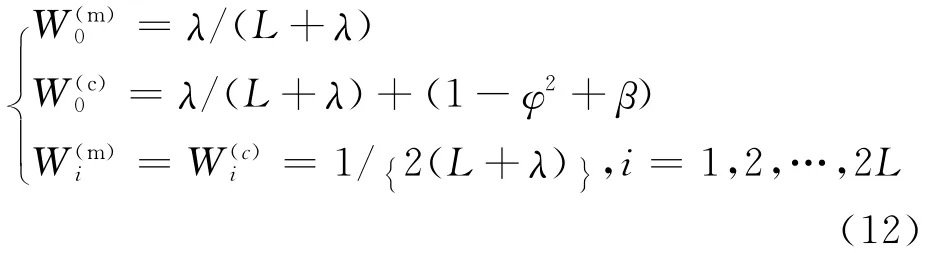
其中，权Wi由下式给出：其中，β为状态分布参数，对于高斯分布，β＝2是最优的。如果状态变量是单变量，则最佳的选择是β＝0。

3.2 迭代UKF（IUKF）滤波算法

将UT变换应用于Kalman滤波，就可以得到UKF滤波算法。将UKF滤波算法状态估计结果Xk重新进行UT变换，计算滤波的参数，再次利用观测值改善对状态的估计结果，这样就得到了迭代UKF算法。

对于非线性的状态方程和测量方程：

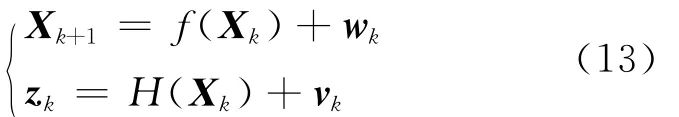
对于本文研究的导弹主动段的跟踪问题，上式中的状态方程就是2.1节中的方程（6），测量方程就是2.2节中的方程（8）。对于状态变量Xk的估计，首先由k时刻的UKF算法计算得到状态估计和协方差分别为＾Xk和P－k，由＾Xk和Pk生成的新采样点可重新求得滤波器的增益Kk，再利用观测值对状态估计进行改善，具体步骤如下：

（1）初始化。

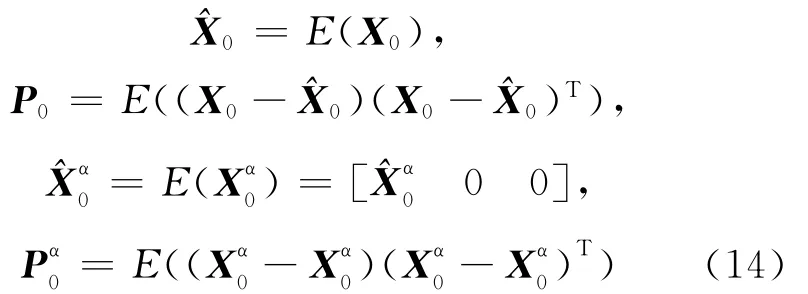
（2）计算采样点。

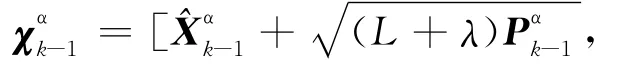
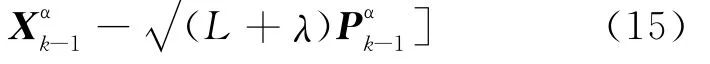
（3）时间更新。

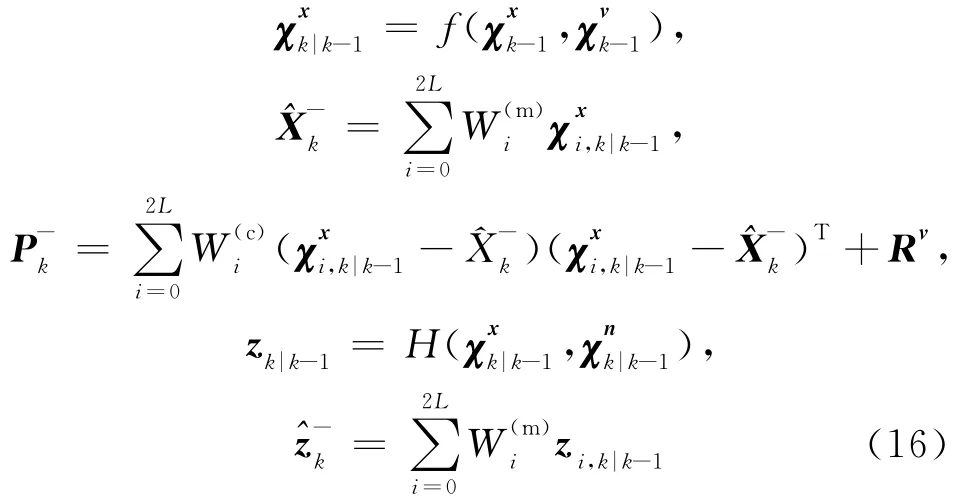
（4）测量更新。

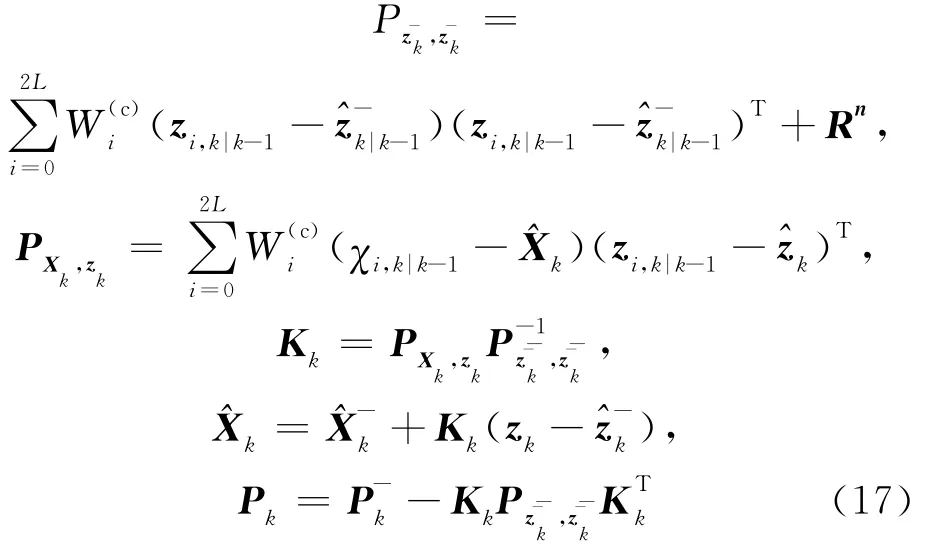
其中，Rv为系统状态噪声方差，Rn为系统测量噪声方差，xα＝ ［xTvTnT］。

（5）重新计算采样点，更新估计结果。

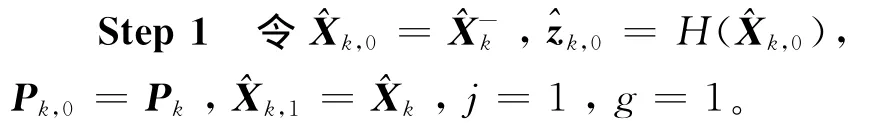
Step 2 定义：

Step 4 j＝j＋1，g＝η·g，重新计算采样点：

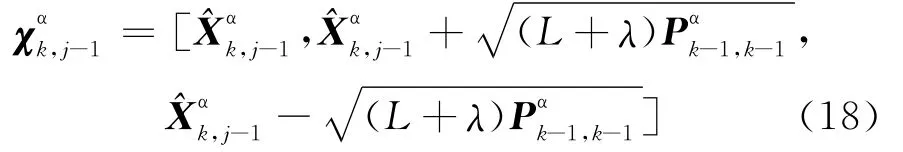
将公式（18）代入公式（16）和公式（17）式重新计算滤波参数，得到新的估计结果：

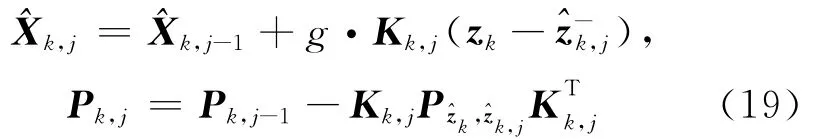
转向Step 2。

最后将公式（19）作为k时刻的滤波状态和协方差估计结果。

在上述IUKF算法流程中，为满足迭代要求，一般取0＜η≤1。

与UKF算法相比，IUKF算法增加了迭代测量更新运算，每次迭代增加的运算量主要是样点的非线性变换。总体来说，IUKF算法比UKF算法增加了一些计算量，但其计算复杂度仍然为同一量级。由于不同的非线性变换形式带来的计算量有较大不同，这将影响IUKF算法与UKF算法之间计算量的差别。

4 仿真实验

在仿真计算机CPU为P4双核、2.7GHz、内存为1GB的情况下，使用Matlab工具进行仿真计算。仿真实验中，测量数据间隔Ts取0.5s，视线测量误差σLOS分别取30μrad和60μrad。目标为某2 000km弹道导弹，主动段飞行时间为100s，首次观测时间为第20s。选取两颗地球同步轨道卫星观测。Monte－Carlo次数为50次。图3是测量数据间隔为0.5s、σLOS为30μrad情况下UKF算法和IUKF算法对目标速度和位置的跟踪误差仿真结果。图4是测量数据间隔为0.5s、σLOS为60 μrad情况下UKF算法和IUKF算法仿真结果。

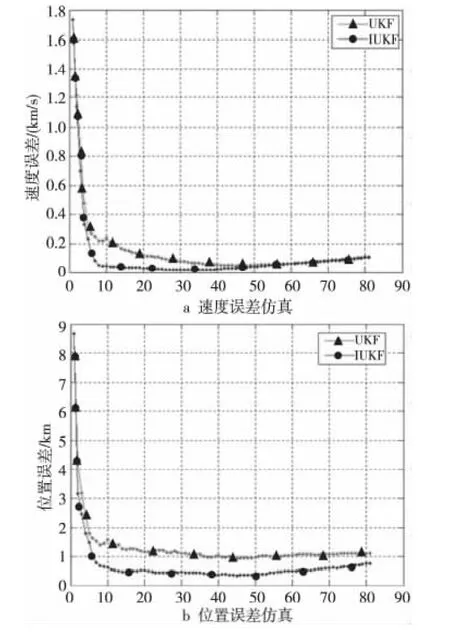
Figure 3 Simulation results of UKF and IUKF whenδLOS ＝30μrad图3 σLOS取30μrad时UKF与IUKF仿真结果

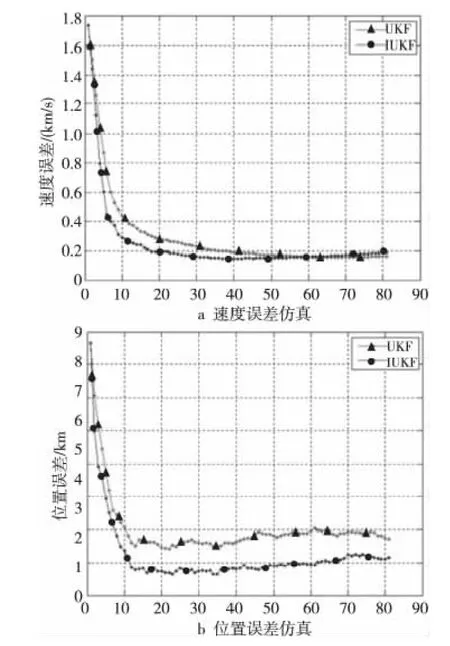
Figure 4 Simulation results of UKF and IUKF whenδLOS ＝60μrad图4 σLOS取60μrad时UKF与IUKF仿真结果

从图3和图4的仿真结果可以看出，IUKF算法对新的观测值反应更迅速，在相同的仿真条件下，IUKF算法比UKF算法收敛速度更快、收敛精度更高。

5 结束语

本文围绕卫星在仅有角度测量信息下弹道导弹的主动段跟踪问题，对常用的非线性滤波UKF算法进行改进，提出了IUKF算法。采用重力转弯模型建立主动段状态方程，结合UKF算法与IUKF算法进行仿真实验。实验表明，本文提出的方法收敛速度更快、收敛精度更高，适用于基于卫星角度测量信息下导弹目标主动段跟踪的应用。

［1］ Danis J.Space－based tactical missile launch parameter estimation［J］.IEEE Transactions on AES，1993，29（2）：412－424.

［2］ Li Yi－cong，Kirubarajan T，Bar－Shalom Y，et al.Trajectory and launch point estimation for ballistic missiles from boost phase LOS measurements［C］∥Proc of IEEE Aerospace Conference，1999：425－442.

［3］ Bellaire R L，Kamen E W，Zabin S M.New nonlinear iterated filter with applications to target tracking［C］∥Proc of the SPIE’95，1995：240－251.

［4］ Van Zandt J R.Boost phase tracking with an unscented filter［C］∥Proc of the SPIE’02，2002：263－274.

［5］ Zhan Rong－hui，Wang Ling，Wan Jian－wei.Research on robust algorithm for single observer passive target tracking［J］.Signal Processing，2007，23（3）：464－468.（in Chinese）

［6］ Li X R，Jilkov V P.Survey of maneuvering target tracking part II：Motion models of ballistic and space target［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46（1）：96－119.

［7］ Li Dun.Target location and prediction with space early warning system［D］.Changsha：National University of Defense Technology，2001.（in Chinese）

［8］ Julier S J，Uhlmann J K，Durrant－Whyte H F.A new method for the nonlinear transformation of means and covariances in filters and estimatimators［J］.IEEE Transactions on Automatic Control，2000，45（3）：477－482.

［9］ Wan E A，Merwe R，Nelson A T.Dual estimation and the unscented transformation［M］∥Advances in Neural Information Processing Systems 12，Cambridge：MIT Press，2000：666－672.

附中文参考文献：

［5］ 占荣辉，王玲，万建伟.稳健的单站无源目标跟踪算法研究［J］.信号处理，2007，23（3）：464－468.

［7］ 李盾.空间预警系统对目标的定位与预报［D］.长沙：国防科学技术大学，2001.