基于变胞并联机构的多维隔振研究

牛军川, 杨 峰, 李 勇

(山东大学 机械工程学院 高效洁净机械制造教育部重点实验室,济南 250061)

在诸如车辆、船舰、潜水艇和航天器等机械设备中存在大量的振动和冲击，它们严重影响着机械设备的工作性能和寿命[1]，必须对其采取行之有效的隔振措施。然而，由于这些机械设备一般都在变环境和变工况条件下工作，并且其振动一般都为多维振动，传统的隔振理论、隔振技术和隔振系统在解决这类隔振问题时存在很多的缺陷。在这中间，最重要的缺陷是传统的隔振理论是基于传统的线性隔振系统，其动力学特性不能随着激励和外界环境的变化而改变，另外，由于传统的隔振系统采用诸如橡胶等传统隔振器直接安装于振源与接受体之间，工程上一般是针对沿隔振器轴线方向的振动进行隔振设计，因此也不能很好满足实际工程中对多维振动进行隔离的要求。

近些年来，随着并联机构的发展，有些学者已经开始应用一些比较简单的并联机构减振平台进行多维振动的隔离，获得了一些结果，结果表明，这些并联机构在隔离多维振动方面有着较好的效果[2-5]。然而，传统的并联机构在制造、安装完成以后，其机构尺寸和拓扑结构就已固定，其自由度和工作空间亦不能调整，因此也就难以适应工作条件的变化，致使其应用范围受到了限制[6]。1998年，在第25届ASME机构学与机器人学双年会上Dai等人正式提出了变胞机构的概念，该类机构具有高度可缩性和可展性，可改变杆件数、自由度以改变机构拓扑图，为隔离变工况、变环境的多维振动提供了一种全新的思路。

救护车等在崎岖路面上行驶、启停、拐弯等操作过程中，会使担架系统存在前后、左右、上下甚至是俯仰等多维振动，为实现担架系统的多维振动控制，本文通过引入一个变胞铰链，给出了一种新颖的变胞机构，该变胞能转化为3自由度的并联机构或者是4自由度的并联机构。这里将该变胞机构用作多维减振平台的主体机构，推导了其运动学和动力学方程，研究了其动力学特性和隔振特性。

1 隔振平台模型

如图1所示，为某一可变胞并联机构，这里将其作为多维隔振平台的主体机构。该机构由上、下两个平台组成，一般上平台为动平台，下平台为静平台。该机构的连杆系统有三条支链，每条支链为一个操作器。这里，在上平台铰链A3处引入一个变胞运动rT铰链[8]，如图2所示，该铰链有两种配置：① 当rT铰处于第一配置时，如图2(a)所示，rT铰存在两种转动，也就是轴1与y方向平行，可转动，轴2与x方向平行，该轴亦可转动；② 当十字轴绕轴1转动至图2(b)所示形位时，轴2和z方向平行，则rT铰处于第二配置时，rT铰只存在一种转动，也就是轴1仍旧与y方向平行，可转动，轴2则不再与x方向平行，该轴的转动被固定。

用C表示圆柱副，R表示转动副，则图1中A1，B1，C1为圆柱副，A2，B2，C2、B3，C3为转动副，A3为rT铰。当rT铰处于第一形位时，A3为A31和A32两个转动副的复合，当rT铰处于第二形位时，A3只存在一个A32转动副。容易看出，图1的变胞并联机构有两个CRR操作器和一个CRrT操作器三条支链。

分析和自由度计算表明，当rT铰取第一配置，则变胞机构处于第一形位，变胞机构等价于一个3-CRR并联机构，该机构具有3个平移自由度。当rT铰取第二配置时，则变胞机构处于第二形位，该变胞机构等价于一个CRU-2CRR并联机构，该机构有三个平移自由度和一个转动自由度。第一和第二配置的相互转换可以根据环境和工况要求通过自动或手动设置实现。

圆柱副A1和B1、转动副C1和A31被用作机构的主动副，主动副和固定平台之间用弹簧阻尼器系统连接，如图1所示。

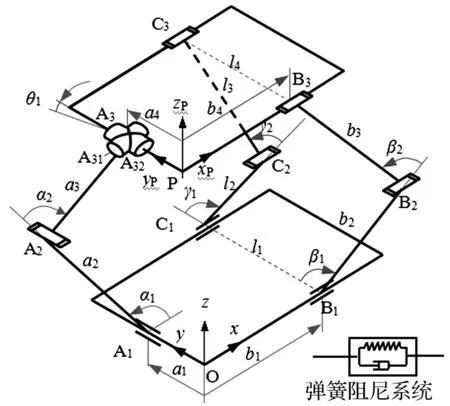
图1 变胞并联机构模型

图2 rT铰的配置

2 运动学和动力分析

2.1 运动学

如图1所示，将系统的全局坐标o-xyz放在下平台上，上平台的局部坐标放在P点上，机构配置及其尺寸等都在图中进行了标注。

根据图1所示动力学模型及其几何配置关系，如果rT处于图2(a)所示的第一配置，则如上所述，机构为第一形位，机构为一具有四自由度的CRU-2CRR并联机构。这里设定A1、B1为主动移动副和C1、A31为主动转动副，这时，如果给定参数a1、b1、γ1和θ1，可容易得到该并联机构的运动学正解表达式如下:

(1)

对式(1)求关于时间t的导数，则可得上平台参考点P的速度为

(2)

(3)

那么，第一阶运动影响系数G1可以用下面的表达式来计算

(4)

这里F1={f1,f2,f3,f4)，d1={a1,b1,l1,θ1}。

类似地，如果rT铰取图2(b)所示的第二配置，则变胞机构处于第二形位，机构变为一三自由度的3-CRR机构，其正运动学方程式为

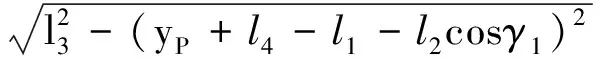
(5)

从式(5)容易看出，式(5)仅是式(1)的一个特例，或者说只需设θ1=0，则式(1)就立即退化为式(5)，这时，铰链A3就变成了A32，轴2的转动2被固定，但轴1的转动1仍旧被保留，如图2所示。因此，3-CRR机构是CRU-2CRR机构的退化机构，简单起见，在下面的分析中只给出第一形位即CRU-2CRR机构的分析和方程。

2.2 动力学

本文研究的机构的是一个复杂的非线性动力学系统，因此对其动力学分析和固有频率求解是非常复杂的。另外，由于上平台质量远比连杆和滑块的质量大，简单起见，这里把连杆和滑块等的质量忽略掉，只考虑可动的上平台质量。采用如下的Langrage方程

(6)

推导CRU-2CRR机构的动力学支配方程。这里si是广义坐标，T是动能，V是势能，D是阻尼损耗因子，Γi是沿或绕si方向的广义力，i=1,2,…,n。计算系统的动能和势能并将其带入式(6)中，则得系统第一形位的动力学方程为

(7)

式中:s1为上平台参考点P的广义坐标，Γ1系统的广义力矢量，M1,C1,K1为全局系统的质量矩阵、阻尼矩阵和刚度矩阵。系统的质量矩阵为

M1=diag(mp,mp,mp,Ix)

(8)

这里mp是上平台质量，Ix是上平台绕x轴的转动惯量。系统的阻尼矩阵为

(9)

(10)

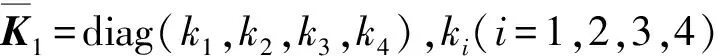
根据式(4)和式(10)，容易知道K1随上平台位置的改变而变化，因此式(7)是一个非线性方程，当上平台处于某一瞬时位置时，相应地系统存在瞬时固有频率。换句话说，如果上平台在某一位置做微幅振动，可以通过求解式(7)获得系统在这一位置的固有频率。

为了获得减振机构的固有频率，忽略阻尼影响，将一组简谐解带入式(7)，可以得到系统的特征方程为

(11)

求解式(11)可以得到系统在这一位置的所有的固有频率ωni(i=1,2,3,4)。

上面求解的过程是基于变胞机构第一形位或者CRU-2CRR机构，根据两形位之间的关系，容易知道，只需把第一形位的机构的4×4维G1,M1,C1,K1等矩阵的最后一行和最后一列去掉，变成3×3维矩阵，则系统为第二形位，式(7)亦退化为第二形位或者3-CRR机构的支配方程。

3 仿真和分析

当变胞机构处于第一形位，即为CRU-2CRR并联机构时，机构的尺寸参数取为：a2=a3=b2=b3=l2=l3=13 cm，l1=l4=20 cm，a4=10 cm，b4=12 cm，上平台质量为5 kg，上平台绕x轴的转动惯量为5 kg·m2。参考点P的坐标为(xp,yp,zp,αp)=(0, 0, 13, 0)。

在点O和A1之间、O和B1之间安装拉压弹簧，弹簧刚度分别为k1=8 000 N/m和k2=2 000 N/m。另外，在铰链C1和A31上安装扭转弹簧，弹簧刚度分别为k3=900 N·m/rad和k4=5 000 N·m/rad。根据静力平衡条件可知，当上平台参考点P处于(0, 0, 13, 0)时，上平台处于静平衡位置，且上平台平行于下平台。

3.1 模态分析

模态分析时，下平台是静平台，上平台是动平台。根据式(11)，可以得到机构处于第一形位时机构的四个模态阵型及其相应的四个固有频率，也就是CRU-2CRR的四个固有模态。按照上面的讨论，仅需要缩减式(7)中各矩阵的相应维数，再进行特征方程的求解，便可以得到3-CRR系统的三个固有频率和固有阵型。两个机构的固有频率及其固有阵型列于表1中。

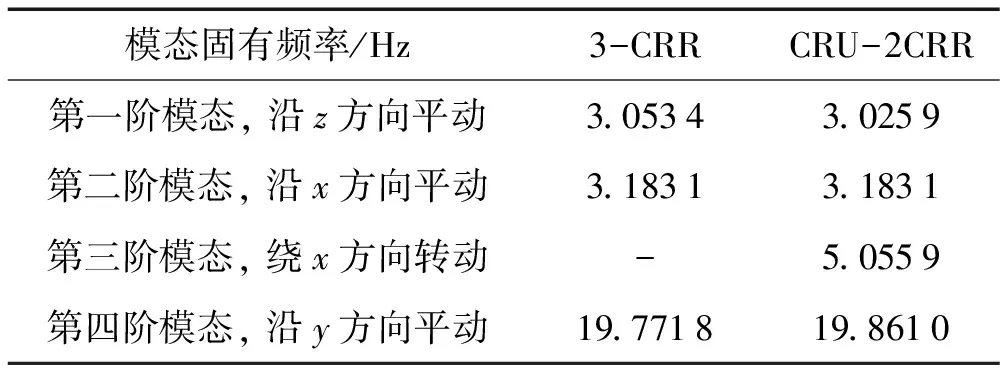
表1 3-CRR和 CRU-2CRR机构的模态

容易看出，CRU-2CRR机构有沿x，y，z方向的三个平动自由度和一个绕x轴的转动自由度，这个转动自由度在3-CRR机构中消失。CRU-2CRR机构的固有模态阵型如图3所示。从图3和表1中可知，CRU-2CRR机构的第二阶模态几乎是沿x方向的纯平动，该模态与其它方向的振动不耦合，其它三个方向的模态则不是沿(或绕)某坐标轴的纯平动(或转动)，它们之间存在轻微耦合。对于变胞机构的第二形位，或者3-CRR并联机构，只存在如图3(a)、(b)和(d)所示的三个模态，相应的固有频率如表1中所示。

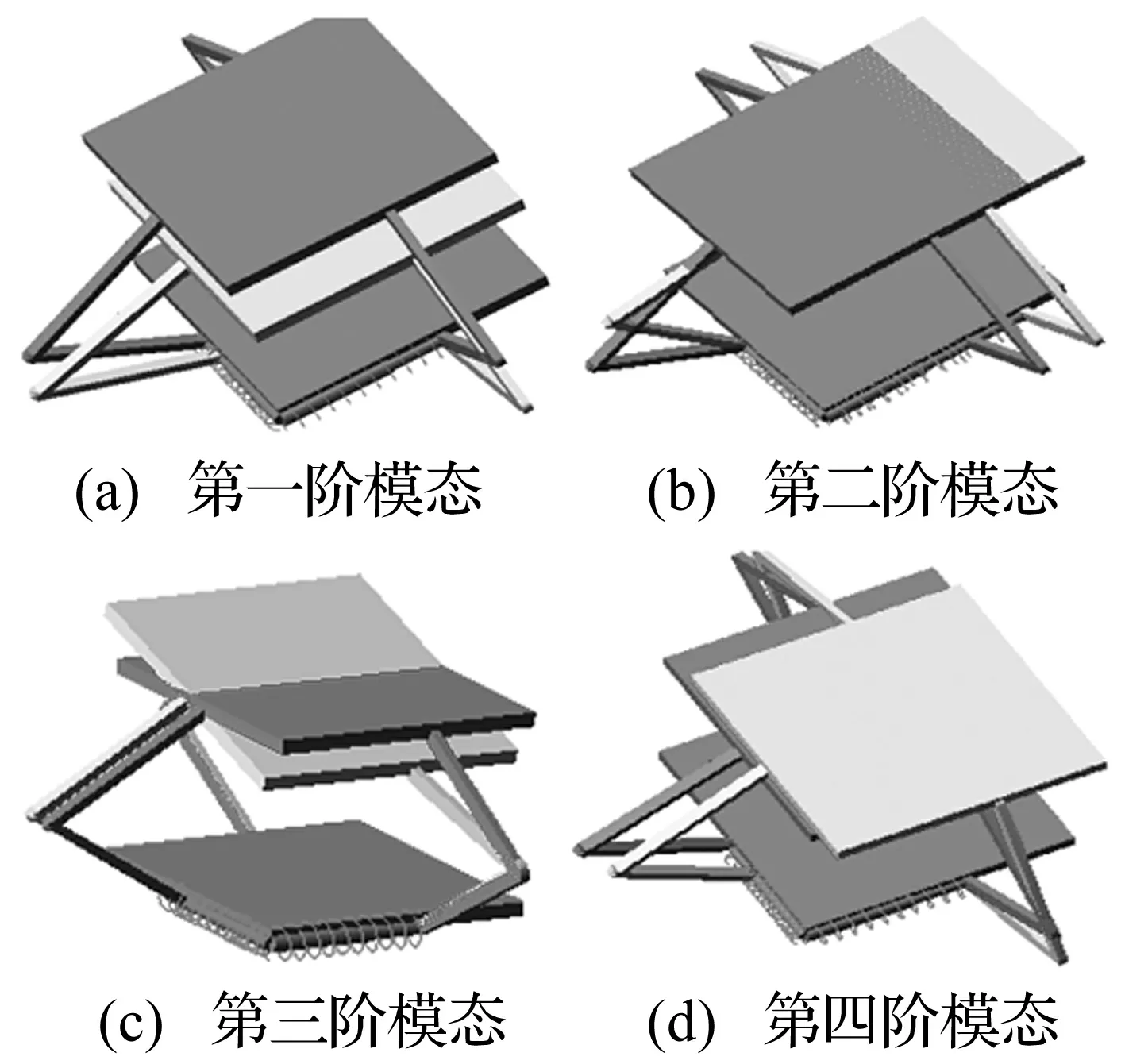
图3 第一形位时系统的模态阵型

3.2 振动隔离

为了验证建立的变胞并联减振平台的隔振效果，采用Matlab和Adams基于CRU-2CRR机构进行仿真研究。这里假设激励来自于下平台的运动，这时下平台被放开，所加的速度激励函数为0.001sin(200 t)，分别施加在下平台沿x，y，z方向和绕x轴方向上。表2给出了上、下平台加速度的最大值和有效值(均方根)。可以看到，上平台的加速度有效值相比下平台有较大的降低，可见，多维隔振平台在隔离多维振动方面具有较好的隔振效果。

从时间历程上，作为例子，仅考虑下平台z方向的激励和振动，z方向的上、下平台的加速度如图4所示。在图中明显可以看出，上平台的振动加速度比下平台的振动加速度有较大的降低。从上面的频域和时域分析易得，本文变胞并联机构的两个形位对隔离来自下平台的振动有很好效果。

同样的仿真和分析表明，该并联机构可以隔离来自下平台的各个方向的多维振动。并且可以通过进一步的研究得到每个振动方向上使系统隔振有效的最小频率，如表3中所示。从表中可知，最小频率和固有频率的频率比大约等于1.414，这个结果类似于传统单自由度隔振系统中的结论。

表2 上下平台的加速度

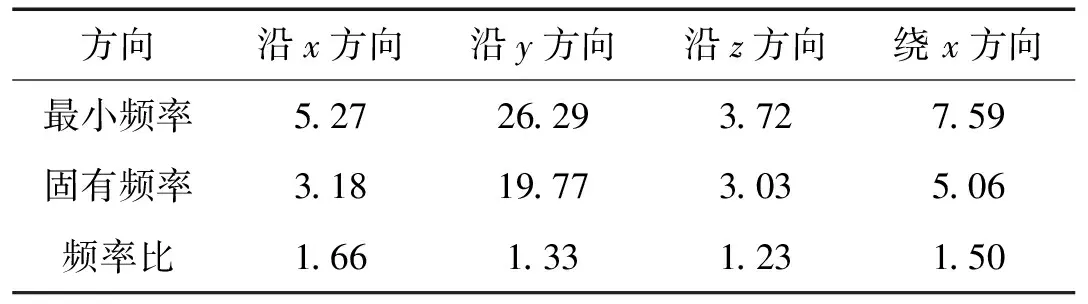
表3 激励频率、固有频率及其频率比

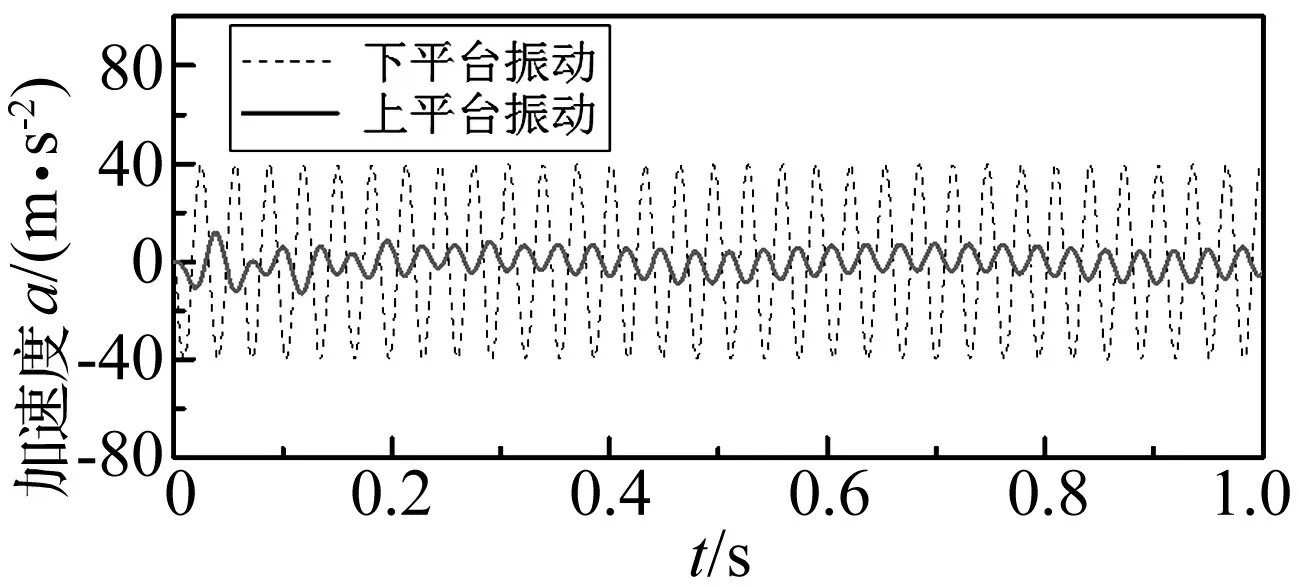
图4 在z方向上的下平台和上平台加速度时间历程

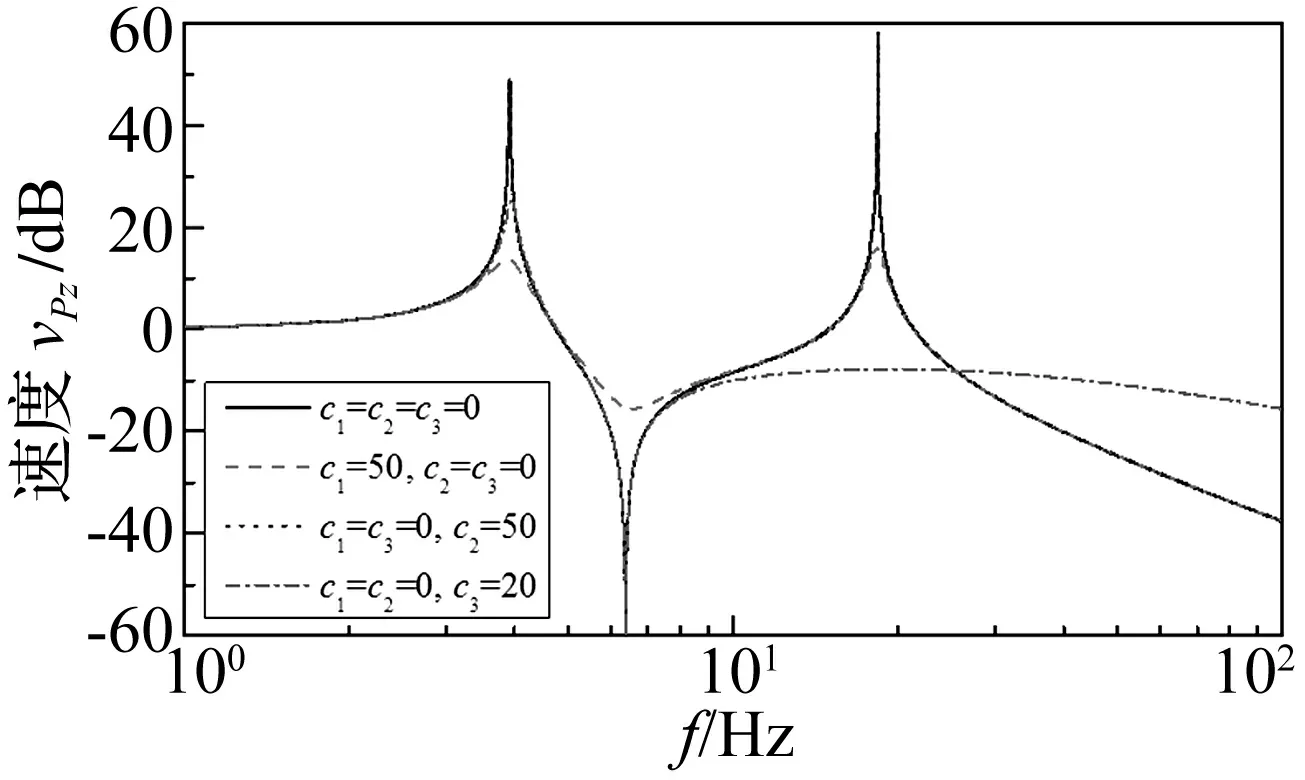
图5 在下平台施加速度激励时上平台的速度响应

图5是在下平台施加速度激励时上平台的速度响应。从图中可得如下结论：① 如果下平台也是运动的，对比图5峰值和表1数值，由于耦合，系统的固有频率将会有所偏移；② 在第一个弹簧上即A1处施加阻尼c1=50 N·m/s，速度频率响应幅值将会降低；③ 在第二个弹簧上即B1处施加c2=50 N·m/s的阻尼，阻尼对z方向振动几乎没有影响；④ 在第三个弹簧上即C1处施加c3=20 N·m/s的阻尼，扭转弹簧的阻尼对降低速度振幅具有很好的作用，特别是对第二个峰值，该峰值完全被抑制，然而随着频率的增加，隔振效果则变坏。

4 结 论

引入了一个变胞运动的rT铰链，在并联机构的基础上综合出了一种变胞并联机构。将该变胞机构作为多维隔振系统的隔振主体，在选定的主动副处安装弹簧阻尼系统，构建了可变胞并联机构减振平台，该变胞机构可以通过调整rT铰的配置或形位，使变胞并联机构在3-CRR和CRU-2CRR机构之间相互转化。

给出的变胞并联减振机构为振动控制提供了一种新的思路和策略。通过对系统的模态、动力学特性和隔振效果的研究表明：① 所给并联机构的固有频率随动平台的位置的变化而改变；② 可以通过设定合适的参数调节固有频率，从而可以使激励频率避开固有频率，抑制振动；③ 所给变胞并联机构在两个形位上都可以实现较好的隔振效果，它可以隔离两种工况的多维振动。

参 考 文 献

[1]牛军川, 宋孔杰. 多激励多支承全柔性隔振系统的传递特性分析[J]. 机械工程学报, 2011, 47(7): 59-64.

NIU Jun-chuan, SONG Kong-jie. Transmission characteristics of fully flexible Isolation systems subjected to multi-excitations and supported by multi-mounts[J]. Journal of Mechanical Engineering,2011,47 (7): 59-64.

[2]马履中, 杨启志, 尹小琴,等. 仿橡胶多自由度弹性阻尼减振装置研究[J]. 机械工程学报, 2004, 40(1): 21-24.

MA Lü-zhong, YANG Qi-zhi, YI Xiao-qing, et al. Analysis of combined elastic damping devices on multiple DOF parallel mechanism[J]. Journal of Mechanical Engineering, 2004,40(1): 21-24.

[3]余顺年, 马履中, 陈扼西, 等. 三自由度并联机构位置和运动分析及仿真[J]. 农业机械学报, 2005, 36(9): 97-100.

YU Shun-nian, MA Lü-zhong, CHEN E-xi, et al. Position and kinematics analyses and simulation of a 3-DOF parallel mechanism[J]. Transactions of the Chinese Society of Agricultural Machinery, 2005,36(9):97-100.

[4]杨峰, 牛军川, 李勇. 可调频并联减振机构的动力学分析与应用研究[J]. 现代振动与噪声技术, 2012, 10: 112-115.

YANG Feng, NIU Jun-chuan, LI Yong. Application and dynamics of tunable parallel mechanism for vibration reduction[J]. Modern Vibration and Noise Techniques, 2012,10:112-115.

[5]Yang F, Niu J C, Li K P, et al. Study on frequency tuning of parallel mechanism for reducing vibration[J]. Applied Mechanics and Materials, 2013,275-277: 905-908.

[6]杨峰. 一种可变胞并联机构的多维隔振平台研究[D]. 济南：山东大学，2013.

[7]Dai J S,Rees J J. Mobility in metamorphic mechanism of foldable/erectable kinds[C]. The 25th ASME Biennial Mechanisms and Robotics Conference,1998, Baltimore, New York, USA.

[8]Gan D, Dai J S， Liao Q. Constraint analysis on mobility change of a novel metamorphic parallel mechanism[J]. Mechanism and Machine Theory,2010,45(12):1864-1876.