基于动态输出反馈的半车主动悬架系统鲁棒控制

李 荣, 焦晓红， 杨 超

(燕山大学 电气工程学院，秦皇岛 066004)

传统的被动悬架不能适应变化的行驶工况，不利于汽车平顺性提高。因此，近十年国内外研究机构和各大汽车厂商纷纷展开了对半主动[1-4]、主动[5-7]悬架系统的研究。相对半主动悬架而言，主动悬架可以根据路面状况和汽车运行状态，实时调整控制器的参数，改变悬架控制力的大小，抑制车身的振动。因此，针对主动悬架模型，考虑作动器的动态特性，设计控制器，在存在外界干扰的情况下，最大程度地吸收来自路面的冲击，同时满足乘坐舒适度和操作稳定性的要求，是近期汽车主动悬架控制问题研究的主要方向。另外，实际悬架系统中并不是所有的物理状态变量都适合使用传感器直接测量得到，这就使得全状态反馈的控制方法难以实现。近年来许多研究者针对此问题开展了相应的研究。例如，张玉春等[8]将悬架系统和电液作动器分为内外两个回路控制，悬架为外回路采用滤波输出反馈控制，电液作动器为内回路采用PI控制。陈红等[9]将电液作动器和悬架系统整体作为线性系统，给出了一种H2/广义H2输出反馈控制策略。文献[10-13]均未考虑作动器部分，直接针对半车主动悬架系统进行控制：文献[10-12]考虑在车身俯仰角运动范围不大的状况下悬架为线性系统，王娟等[10]给出了滚动时域H∞输出反馈控制策略，刘树博[11]采用差分进化算法和LMI相结合，设计了H∞/广义H2静态输出反馈控制器，宋刚等[12]提出了时域硬约束条件下的H∞输出反馈控制策略；文献[13]先利用T-S模糊模型线性化俯仰角的非线性，然后给出了基于观测器的H∞控制策略。值得注意的是：以上研究都没有考虑作动器的本征非线性；另外，悬架系统的可测物理量多选取为：车辆系统悬挂质量的垂直速度(通过加速度传感器信号积分获得)、前后悬架动行程(由位移传感器测量)。不考虑作动器非线性设计控制器，将使得闭环系统的实际控制性能的鲁棒性受到限制；而悬架系统中传感器的使用除了考虑传感器安装的便捷，还应考虑传感器的成本和精度问题。

基于以上分析，本文以作动器和悬架系统为被控对象，针对作动器中存在的非线性、悬架系统状态量不可测以及外部干扰的情况，提出了一种动态输出反馈鲁棒干扰抑制控制策略。通过理论推导和仿真研究证明所设计控制器的有效性，并通过和PID控制算法相对比，进一步说明所设计的控制器能提高汽车的行驶平顺性和操纵稳定性。

1 半车主动悬架系统数学模型和控制问题

1.1 半车主动悬架系统数学模型

假设汽车的左右两侧以完全相同的方式运动，同时汽车处于俯仰状况，对系统进行简化，则半车悬架系统物理模型如图1所示[5]。

图1 半车主动悬架系统模型结构特征示意图

图中，Ff,Fr为前后垂直力，Mb,Muf,Mur分别为车体质量和前后簧下质量，θ为车身的俯仰角，l1,l2分别为车体重心到前后轮之间的轴距，h为车体重心位移，Kaf,Kar,Caf,Car分别为前后悬架系统的刚度系数和阻尼系数，Ktf,Ktr为前后车轮的轮胎刚度系数，xsf,xsr,xuf,xur,xrf,xrr分别为前后车体位移、车轮位移和路面位移，Of,Or前后液压负载流量。

车体静止时车体重心位移和角位移位于原点，运用牛顿第二定律得车体运动方程为：

(1)

(2)

前后簧下质量的运动方程为：

(3)

在车身俯仰角θ运动范围不大时，前后车体位移为：

xsf=h-l1sinθ≈h-l1θ
xsr=h+l2sinθ≈h+l2θ

(4)

对前后车体进行动力学分析，得到：

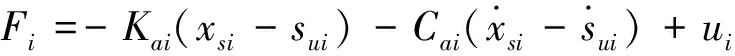
(5)

其中：Jy为车体重心惯性力矩，i分别取f,r时代表前后。前后液压作动器提供的控制力uf,ur为：

ui=S·PLii=f,r

(6)

前后液压缸负载压降PLf,PLr的微分与Qf,Qr的关系：

(7)

(8)

其中：S为活塞面积，Vt是总的作动器的容积，βe是液体的有效体积弹性模量，Ctp是活塞的总泄露因子，Cd是流量系数，σ是伺服阀面积梯度，ρ是液体的密度，Ps是液压系统的供油压力，xvf,xvr分别为前后液压缸伺服阀位移，分别由相应的输入电压u1,u2控制：

(9)

1.2 控制问题形成

一般情况下，液压作动器中缸内压力和伺服阀位移是很方便利用传感器直接测量的，而车体重心位移与速度、前后车轮位移与速度及车身俯仰角与角速度却不方便用传感器测量，这里除了考虑到传感器安装的便捷还有传感器的成本和精度问题。因此，控制系统设计的重心就变成了：如何只利用可测的液压作动器缸内压力和伺服阀位移，通过设计的控制策略使闭环反馈控制系统具有满意的控制性能。

为此，选取系统状态变量：

并将系统状态分成两部分：不可测量部分X1=[x1,…,x8]T和可直接测量部分X2=[x9,…,x12]T，则主动悬架系统的动态特性方程写为如下形式：

(10)

其中：y为输出信号，包含了所有可直接测量状态，u=[u1u2]T，w=[w1w2]T=[xrfxrr]T代表路面的干扰激励。

另外，考虑到实际系统的特性：x9、x11为液压缸实际压力，肯定小于油源的最大压力，即应有|Ps-sgn(x10)x9|≤2Ps和|Ps-sgn(x12)x11|≤2Ps，则非线性项f(y)具有如下的性质：

(11)

因此，控制系统设计转化为解决如下控制问题：

针对具有外部干扰及状态量不完全可测的系统(10)，设计一个只利用可直接测量的系统输出信号y的动态输出反馈鲁棒控制器，使得相应的闭环系统：无外部干扰w时在平衡工作点是稳定的；有外部干扰w存在时，系统舒适性和平顺性的各项性能指标受干扰的影响被抑制在γ水平以下，满足控制要求。

2 动态输出反馈鲁棒控制设计

这一节将利用Lyapunov稳定性理论和线性矩阵不等式方法，设计一个动态输出反馈鲁棒干扰抑制控制器来实现系统的控制目的。

命题1：针对满足线性增长条件(11)的系统(10)，如果设计一个形如下式的动态输出反馈控制器：

(12)

其中：K1∈R2×8，K2∈R2×4为设计的反馈增益矩阵，L∈R8×4为可调增益矩阵，可使相应的闭环系统具有如下的运行性能：

(2) 当w≠0时，闭环系统是L2增益稳定的，即干扰对系统性能的影响被抑制在γ水平以下,γ为L2增益。

进一步，矩阵L通过L=P-1N来求得，增益K=[K1K2]∈R2×12利用K=YQ求得。矩阵0

(13)

(14)

其中：

“*”代表对称算子，I是合适维数的单位阵，εi(i=0,1,2)为正常数，ρi>0(i=1,2,…,4)为可调参数。

(15)

构造Lyapunov函数：

V=δTQδ+eTPe

(16)

沿闭环系统(15)的轨迹，V的时间导数为：

(17)

注意到有如下不等式成立，

(18)

根据系统舒适性和平顺性要求，选取系统评价信号：

其中：ρi(i=1,…,6)为加权系数，则有，

(19)

(20)

(21)

其中：

考虑到式(19)-(21)，式(18)满足如下不等式：

(22)

其中：

可见：如果∑1,∑2<0，则由式(16)和式(22)，根据Lyapunov稳定性定理和L2干扰抑制技术，命题中的结论得证。进一步，根据Schur补定理，可知∑1<0,∑2<0等价于不等式(13)和(14)，且N=PL，Y=KQ-1。

3 仿真研究

为了验证所设计控制器的有效性，在MATLAB/ Simulink环境下建立半车悬架系统的仿真模型，仿真中系统各物理参数如表1所示[14]。

表1 系统的参数

并且假设：悬架的动行程约束±0.8 mm，控制信号的约束范围是±5 V。后轮处的路面干扰用前轮干扰的延迟形式表示，即xrr(t)=xrf(t-l/v)，为l=l1+l2前后车轮之间的距离。

本文针对以下两种工况进行仿真：

(1) 汽车以20 m/s的速度驶过C级路面，路面不平度系数Gq(n0)=256×10-6m2/m-1，路面输入为滤波白噪声，C级路面轮廓如图2所示。

图2 C级路面轮廓图

车辆通过有长坡型单凸块的路面，如图3所示，路面不平度输入描述为：

图3 路面激励信号

根据式(13)、(14)得所设计的控制器中的增益矩阵为：

为了更好地说明本文只利用可测的液压作动器缸内压力和伺服阀位移所设计的控制器的控制性能，仿真中与文献中常选取车体重心加速度和后悬架动行程为系统可测输出yi(t),(i=1,2)所设计的PID控制对比。PID控制器设计为：

车身加速度作为衡量乘坐舒适性的指标, 要求垂直加速度和俯仰加速度的幅值分别在4～8 Hz和1～2 Hz的频段内越小越好。因此，仿真中首先给出了在工况1C级路面干扰输入激励下，悬架系统在所设计控制器和PID控制器分别作用下的主动悬架车身垂直加速度和俯仰加速度的功率谱密度(PSD)曲线，如图4所示。显见在1～8 Hz频段，所设计控制器作用下的主动悬架系统的乘坐舒适性比使用重心加速度和悬架位移测量传感器所设计的PID控制有显著提高。

然后给出了系统在工况1和工况2下的仿真时间响应曲线，如图5-7所示。从仿真图5，6可以明显地看出所设计的控制器的性能优于PID控制：图5结果表明，采用动态输出反馈鲁棒干扰抑制控制策略设计的主动悬架经过C级路面时，车体的重心位移、重心加速度和俯仰角、俯仰角加速度都得到了很好的抑制；图6中悬架各指标的相应曲线都没有超出假设的约束范围，前后悬架动行程和加在伺服阀上的电压都在允许范围内， 说明实际的控制输入完全可以满足系统的控制要求，所设计的主动悬架系统能在外部干扰存在的情况下满足期望的控制性能。从图7可以清晰地看出

系统不可测状态变量的估计值能很快地趋近于真实值，表明所设计动态输出反馈控制器的合理性。

图4 垂直加速度和俯仰加速度的功率谱密度曲线

图5 工况1下车体运动相应性能输出

图6 前后悬架动行程轮胎动载荷与伺服阀电压曲线图

图7 工况2下系统不可测状态量的估计值和真实值

4 结 论

本文在充分考虑半车主动悬架系统的非线性和外部干扰的基础上，结合作动器的动态特性和悬架的动力学特性，建立了整体系统的数学模型，并且针对车体位置和速度、车身俯仰角度和角速度、前后车轮位置和速度不可直接测量情况，提出了一种动态输出反馈鲁棒干扰抑制控制策略。这种控制策略很好地解决了系统的非线性和抗干扰性的问题，并且仿真结果表明，所设计的控制器能有效地提高车辆的乘坐舒适度和操作稳定性。

参 考 文 献

[1]张立军, 张天侠. 车辆非平稳状态行驶下的半主动悬架控制[J]. 振动与冲击, 2010, 29(6): 189-193.

ZHANG Li-jun, ZHANG Tian-xia. Semi-active control of vehicle suspension under nonstationary running condition[J]. Journal of Vibration and Shock, 2010, 29(6): 189-193.

[2]董小闵, 余淼, 廖昌荣,等. 具有非线性时滞的汽车磁流变悬架系统自适应模糊滑模控制[J]. 振动与冲击, 2009, 28(11): 55-60.

DONG Xiao-min, YU Miao, LIAO Chang-rong, et al. Adaptive fuzzy sliding mode control for magentorheological suspension system considering nonlinearity and time delay[J]. Journal of Vibration and Shock, 2009, 28(11): 55-60.

[3]Zapateiro M, Luo N, Karimi H R, et al. Vibration control of a class of semiactive suspension system using neural network and backstepping techniques [J]. Mechanical Systems and Signal Processing, 2009, 23(6): 1946-1953.

[4]Poussot-Vassal C, Sename O, Dugard L, et al. A new semi-active suspension control strategy through LPV technique[J]. Control Engineering Practice, 2008, 16(12): 1519-1534.

[5]Huang C J, Lin J S, Chen C C. Road-adaptive algorithm design of half-car active suspension system[J]. Expert Systems with Applications, 2010, 37(6): 4392-4402.

[6]罗鑫源, 杨世文. 基于AHP的车辆主动悬架LQG控制器设计[J]. 振动与冲击, 2013,32(2): 102-106.

LUO Xin-yuan, YANG Shi-wen. Design of a LQG controller for a vehicle active suspension system based on AHP[J]. Journal of Vibration and Shock, 2013, 32(2): 102-106.

[7]王威, 薛彦冰, 宋玉玲. 基于GA优化控制规则的汽车主动悬架模糊PID控制[J]. 振动与冲击, 2012, 31(22): 157-162.

WANG Wei, XUE Yan-bing, SONG Yu-ling. Fuzzy-PID control strategy for an active suspension based on optimal control laws with genetic algorithm[J].Journal of Vibration and Shock, 2012, 31(22): 157-162.

[8]张玉春, 王良曦, 丛华. 电液主动悬架滤波输出反馈控制器的设计及仿真实现[J]. 汽车工程, 2004, 26(3): 325-329.

ZHANG Yu-chun, WANG Liang-xi, CONG Hua. Design and simulation of filtered output feedback controller for electro-hydraulic active suspension[J].Automotive Engineering, 2004, 26(3): 325-329.

[9]陈虹, 马苗苗, 孙鹏远. 主动悬架H2/广义H2输出反馈控制[J]. 控制理论与应用, 2007, 24(5): 790-794.

CHEN Hong, MA Miao-miao, SUN Peng-yuan.H2generali-zed H∞output feedback control for active suspensions[J]. Control Theory and Applications. 2007, 24(5): 790-794.

[10]王娟, 刘志远, 陈虹. 基于LMI的主动悬架的滚动时域H∞输出反馈控制[J]. 汽车工程, 2009, 31(1): 37-41.

WANG Juan, LIU Zhi-yuan, CHEN Hong. Output feedback H∞control combining moving horizon scheme for active suspension based on LMI approach[J]. Automotive Engineering, 2009, 31(1): 37-41.

[11]刘树博. 主动悬架H2/广义H2静态输出反馈控制方法[J]. 中国公路学报, 2009, 22(4): 122-126.

LIU Shu-bo H2/ generalized H2static output feedback control method for active suspension[J]. China Journal of Highway and Transport, 2009, 22(4): 122-126.

[12]宋刚, 吴志刚, 林家浩. 考虑时域硬约束的车辆主动悬架H∞控制[J]. 农业机械学报, 2009, 40(4): 11-17.

SONG Gang, WU Zhi-gang, LIN Jia-hao.H∞control of active suspension with time-domain hard constraints[J]. Transactions of the Chinese Society of Agricultural Machinery, 2009, 40(4): 11-17.

[13]吴忠强, 陈金钉. 基于T-S模型的汽车主动悬架H∞控制研究[J]. 振动与冲击, 2007, 26(11): 64-69.

WU Zhong-qiang, CHEN Jin-ding.H∞control of automotive active suspension based on T-S model [J]. Journal of Vibration and Shock, 2007, 26(11): 64-69.

[14]刘震, 祝晓才. 基于逐步后退法的车辆半侧液压主动悬架最优控制设计与仿真[J]. 国防科技大学学报, 2006, 28(4): 115-120.

LIU Zhen, ZHU Xiao-cai. Backstepping based optimal control design and simulation of hydraulic active suspensions applied to a half-car model[J]. Journal National University of Defense Technology, 2006, 28(4): 115-120.