蜂窝材料率相关本构模型及其在月球探测器中的应用研究
2014-09-05胡建国马大为乐贵高
胡建国, 马大为, 乐贵高, 赵 婕
(1.南京理工大学 机械工程学院,南京 210094;2.甘肃林业职业技术学院 基础部,甘肃 天水 741020)
轻质多孔材料作为一种备选的多功能材料,成为了国内外学者们的研究热点[1]。蜂窝材料作为其中最传统也是最便于制备的轻质多孔材料之一,以其优良的面内、面外力学性能,良好的多功能性和较强的可设计性,在航空、航天、电子、能源等领域中得到了广泛的应用,尤其在星球探测的软着陆缓冲装置中,大量采用蜂窝结构缓冲器来吸收探测器软着陆时的冲击能量[2-4]。
在蜂窝材料数值模拟中,由于蜂窝材料细观结构复杂且尺寸较小,建立真实的数值模型需要耗费大量的计算时间,为了节省数值模拟时间,目前主要采用等效蜂窝材料力学特性的方法。Gibson等[5]提出了胞元模型理论,把蜂窝壁简化成线弹性的Euler-Bernoulli梁模型,推导出正六边形蜂窝芯几何形状尺寸与等效弹性参数的解析表达式,马连华等[6]采用均匀化理论研究了不规则蜂窝夹芯各向异性性质,并给出了蜂窝夹芯面内各等效弹性参数计算公式,翟光等[7]应用三明治等效模型对蜂窝板夹芯进行等效计算,得到了等效物理参数,王闯等[8]运用试验与仿真相结合的方法研究了铝蜂窝的冲击动力学性能,Foo等[9]研究了在低速冲击载荷下蜂窝夹心板的动态响应及破坏准则,Xue等[10]研究了蜂窝夹心板的面外冲击力学特性,并提出了方型蜂窝夹心结构的率相关本构模型,Tagarielli等[11-12]研究了多孔材料力学特性,并提出了泡沫铝横观各向同性等效本构模型。然而,在研究蜂窝等效弹塑性本构模型时,同时考虑蜂窝结构横观各向同性及率相关力学特性的研究开展得不多。
本文在研究蜂窝材料面内面外等效力学特性的基础上,建立了蜂窝结构横观各向同性率相关本构模型;其次,结合有限元法编写了横观各向同性率相关本构模型用户子程序,并进行了子程序的可靠性验证;最后以四腿悬架式探测器为研究对象,研究了缓冲器蜂窝不同率相关系数对探测器着陆过程的影响,研究结果可为探测器缓冲吸能装置及上升器月面起飞稳定性设计提供理论依据。
1 蜂窝材料弹塑性本构模型
Gibson等[5]对多孔固体结构及其性能进行了系统的研究,提出了蜂窝材料的本构模型,并阐述了其变形机理及特性。对于蜂窝材料,由于其蜂窝芯子排列结构的不对称性,面内弹塑性力学特性都是各向异性的,蜂窝芯子轴线方向和垂直于蜂窝芯子轴线方向的面内力学特性有较大差异。
1.1 蜂窝材料相对密度
蜂窝材料的性能取决于相对密度,相对密度系指蜂窝密度与蜂窝基体密度之比。对于等壁厚六边形蜂窝,如图1所示。
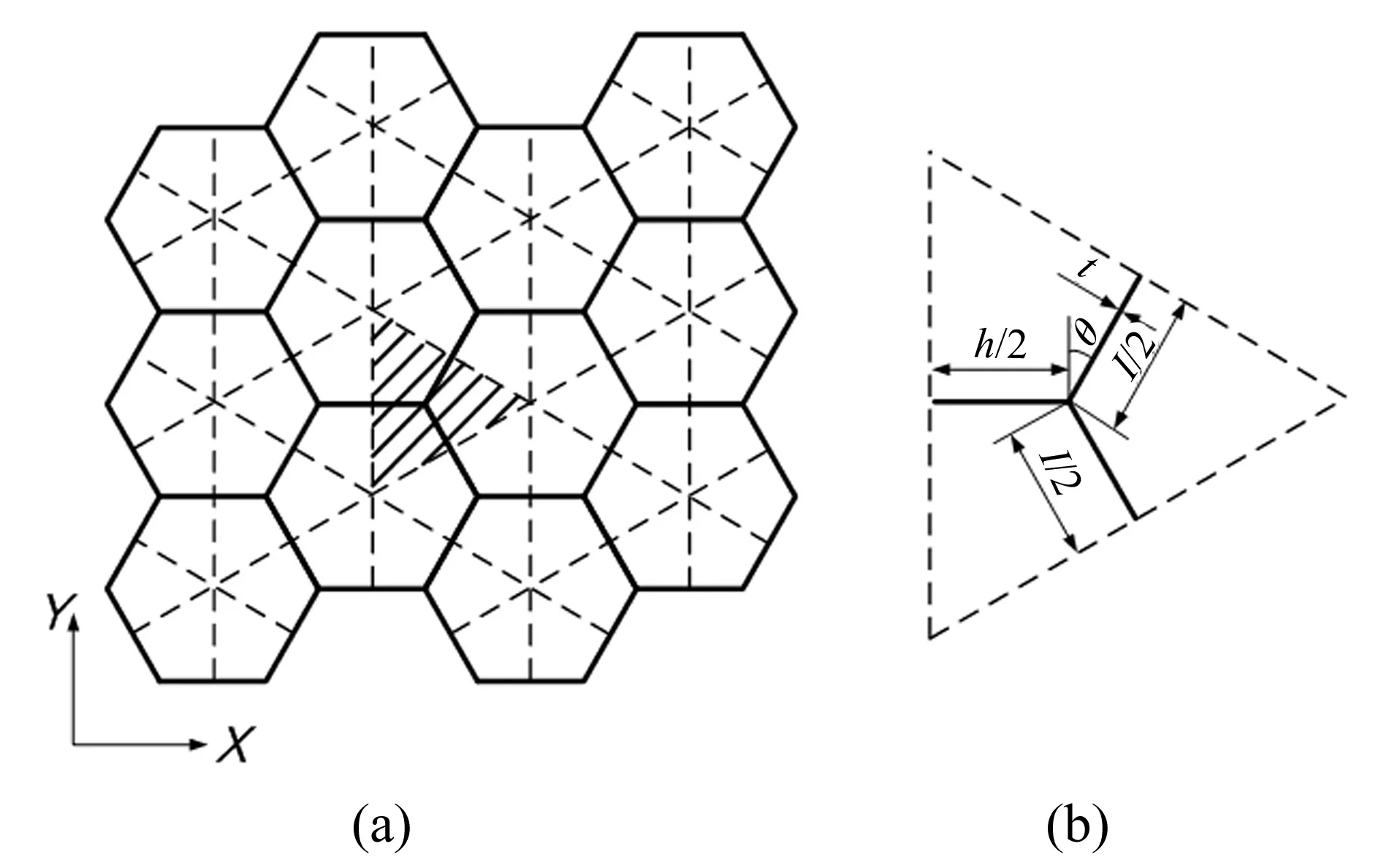
图1 蜂窝结构的分析模型
取阴影部分分析可知,蜂窝密度ρ*为:
(1)
其中,ρs为蜂窝基体的密度,t为胞壁厚度,h和l分别为六边形边长,θ为六边形内角。
1.2 蜂窝材料弹性力学特性
1.2.1 蜂窝面内力学特性
分析一个等壁厚六边形蜂窝胞体受到σx作用时的受力和变形,如图2(a)所示,其倾斜胞壁有弯曲变形,见图2(b),平衡方程为:
(2)
式中:b为胞壁沿Z方向的宽度,将胞壁简化为梁,根据标准梁理论,梁的边界条件为两端均固定约束,可得偏移量为:
(3)
其中,I为胞壁的截面惯性矩I=bt3/12,t为胞壁厚度,
Es为实体材料的杨氏弹性模量。因此,应变可以由平行于X轴方向的分量δsinθ得出:
(4)
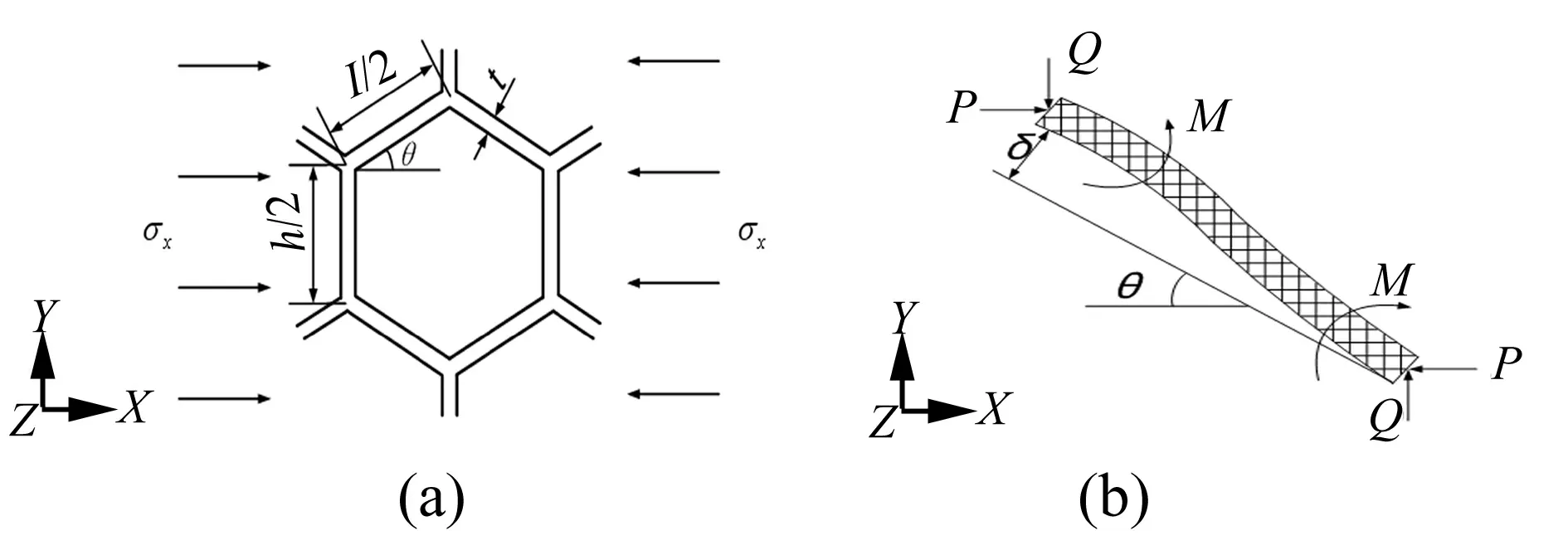
图2 等壁厚六边形蜂窝胞体
则蜂窝结构在X轴方向的面内等效杨氏弹性模量及泊松比为:
(5)
(6)
同理,蜂窝结构在Y轴方向的面内等效杨氏弹性模量与泊松比为:
(7)
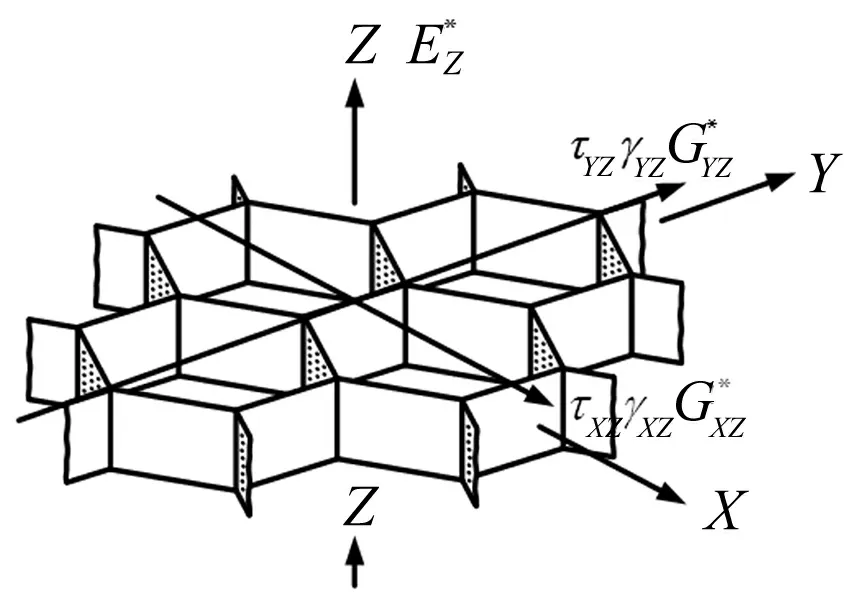
图3 蜂窝面外力学模型
(8)
1.2.2 蜂窝面外力学特性
根据Gibson等[5]的研究,对于如图3所示的蜂窝模型,其面外弹性力学特性如下:
(9)
(10)
(11)
1.3 横观各向同性率相关本构模型
对于等壁厚的正六边形蜂窝,垂直于蜂窝芯子轴线方向的面内等效杨氏弹性模量和泊松比分别相等,即:
(12)
因此,可以将等壁厚正六边形蜂窝视为横观各向同性材料。
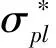

图4 蜂窝应变率效应示意图
对于多孔材料,Tagarielli等[11]提出了横观各向同性率无关塑性本构模型:
(13)
(14)
由于蜂窝的应变率敏感特性,建立率相关本构模型时,屈服函数既是等效塑性应变的函数,也是等效塑性应变率的函数。因此,在Tagarielli塑性本构模型的基础上,并参照寇玉亮等[12]提出的泡沫铝横观各向同性率相关本构模型,定义如下屈服函数f:
(15)
(16)
其中:

且:

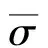
小变形时,由胡克定律可得:
(17)
或
(18)
对于横观各向同性材料,有五个独立的材料参数,且E1=E2,ν31=ν32,G23=G31和G12=E1/[2(1+ν12)]。
在大变形情况下,即塑性变形阶段,选取共旋坐标系,采用空间变形梯度来描述本构方程,根据相关联流动法则,得到:
Dp=ΛN
(19)
D=De+Dp
(20)
其中D为变形率张量,De和Dp分别为弹性和塑性变形率张量,Λ为非负相关联系数,N为屈服面外法线方向张量。根据上述结果,可以得到:

(21)
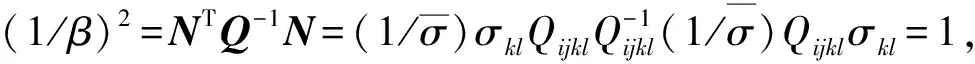
2 横观各向同性率相关本构模型子程序开发及可靠性验证
2.1 子程序开发及可靠性验证
利用ABAQUS/Explicit提供的用户子程序接口VUMAT,将上述率相关本构模型移植到ABAQUS以便于解决具体工程实际问题。
将开发的用户子程序嵌入到ABAQUS软件,然后进行可靠性验证。因为该模型的屈服准则与传统的各向同性Mises屈服准则不同,ABAQUS/Explicit本身并没有模型中定义的等效应力,所以将参数定义如表1所示,使得等效应力退化到Mises应力,在单轴情况下,等效应力即为单轴应力。

图5 压力为0.1 MPa时的σ33云图
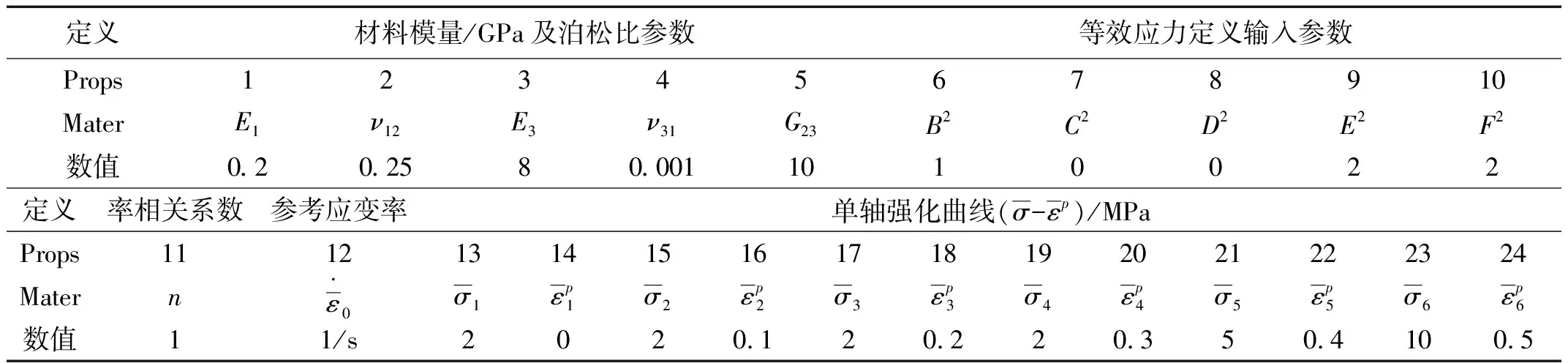
表1 子程序输入参数及材料属性
建立如图5的几何模型,首先将几何体划分成一个单元,设置对称性边界条件,约束1,2方向,然后给3方向一个压力载荷(p=0.1~1 MPa),计算出应力云图如图5(a)所示;然后再将几何体划分为多个单元,计算出应力云图如图5(b)所示,各个小单元中的应力大小一致,且与单个单元计算出的结果相同,所以可认为该子程序的计算结果收敛且稳定。

图6 理论解与子程序有限元解对比
下面将子程序单轴应力-应变曲线的计算结果和理论解进行对比。为体现出该本构模型的应变率效应,计算出了三种不同应变率下的有限元解和理论解对比,如图6所示。
图6中的空心符号代表强化曲线的理论解析解,相应的实心符号代表采用子程序VUMAT得到的有限元计算解。可以看出,实心符号可基本覆盖空心符号,所以子程序的计算结果是准确可靠的,可以用来模拟动态压缩下蜂窝材料的应变率效应。
2.2 子程序VUMAT计算结果与试验结果对比
Shanqing Xu等[16]利用英斯特朗8800液压高速测试系统研究了三种不同相对密度(1.85%,2.69%,4.84%)蜂窝铝在动态冲击下的应变率效应。所得结果表明:在高应变率条件下,不同相对密度的蜂窝材料对应变率的敏感程度不同。本文以相对密度为2.69%的蜂窝铝为例,利用本文开发的率相关本构及其子程序进行有限元模拟,将有限元解和试验值进行对比。
首先,将相对密度为2.69%的蜂窝铝在准静态压缩下的名义应力-应变曲线换算成真实应力和应变曲线,得到其杨氏模量和初始屈服强度,将这些材料参数值和硬化曲线作为子程序VUMAT的参数输入值,拟合出准静态单轴压缩下的应力-应变曲线,如图7所示。可以看出,两者吻合较好。然后,根据相对密度为2.69%的蜂窝铝在不同应变率效应下的真实应力和应变曲线,拟合得到其率敏感系数n。具体确定方法如下:

图7 准静态条件下蜂窝铝单轴压缩应力-应变曲线

图8 不同应变率下蜂窝铝单轴压缩应力-应变曲线
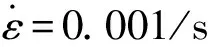
3 蜂窝材料在月球探测器着陆装置中的应用
通过可靠性验证后,将横观各向同性率相关本构子程序VUMAT应用于蜂窝铝的材料属性,模拟蜂窝介质月球着陆缓冲器在着陆过程中的响应,分析不同应变率相关系数对蜂窝缓冲器吸收能量的大小和探测器着陆过程冲击加速度的影响,阐明应变率因素对结构整体抗冲击性能的作用。
这里选择适合于我国航天国情的四腿悬架式月球探测器为研究对象,探测器结构如图9所示,蜂窝缓冲着陆腿结构如图10所示。

图9 月球探测器结构示意图
若探测器总质量M=1 680 kg,初始状态离月面高度H=100 mm,向下冲击速度V=1 800 mm/s,并把月壤视为刚体,足垫与月壤摩擦系数为0.4,子程序输入的材料本构参数见表2。月球探测器中,蜂窝材料的准静态单轴压缩曲线如图11所示。
利用开发的率相关本构模型子程序,分析不同率相关系数对探测器着陆过程的影响,计算结果如图12~图13所示。
图12是单个缓冲器能量吸收随蜂窝率相关系数的变化曲线,在率相关系数小于1的范围内,探测器着陆过程中缓冲器的吸能大小随率相关系数的增加先增大后减小,当率相关系数为0.6时,能量吸收最多。这是因为缓冲器的塑性平台应力随着率相关系数的增大而增大,当塑性平台应力较小时,蜂窝材料较容易达到屈服应力,弹性阶段吸收的能量较少,大部分能量依然靠蜂窝材料塑性变形吸收;但当塑性平台应力较大时,蜂窝材料需要较大的应力才能屈服,在应力增加到屈服应力的过程中,蜂窝的弹性阶段及足垫、缓冲支腿等弹性部件会储存大量的能量,且在屈服之后,随着探测器的速度减小,蜂窝材料的应力很快就小于蜂窝的屈服应力,此后不再产生塑性应变,因此尽管蜂窝的屈服应力较大,但是塑性应变相对较小,吸收的能量反而下降。

表2 蜂窝铝材料参数
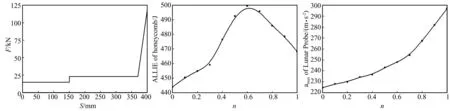
图11 蜂窝铝准静态单轴压缩曲线
图13是探测器着陆过程中的最大冲击加速度随着蜂窝率相关系数变化曲线,探测器最大加速度与率相关系数成近似分段线性关系,当率相关系数增加时,最大冲击加速度亦随之增大,在n<0.6时,增长幅度较慢;但当0.6
4 结 论
(1) 根据蜂窝材料的物理力学特性,将等壁厚正六边形蜂窝等效为横观各向同性体,并建立了横观各向同性率相关弹塑性本构模型;
(2) 结合有限元理论及ABAQUS软件子程序的相关约定,采用显式算法,编写了适合冲击载荷下的横观各向同性率相关材料用户子程序VUMAT,将有限元仿真结果和解析解进行对比,验证了子程序的稳定性和可靠性,表明此等效本构模型可用于多个单元以及复杂载荷状态下的工程仿真计算;
(3) 应用开发的用户子程序对蜂窝在动态冲击下的应变率效应进行了仿真分析,并与试验结果对比,验证了此用户子程序的有效性,同时也给出了根据试验结果率相关系数n的确定方法;
(4) 在探测器蜂窝材料缓冲器的缓冲性能研究中,当率相关系数增加时,缓冲器吸收的能量先增大后减小,并在n=0.6时缓冲器吸收的能量最大;
(5) 在着陆过程中,探测器的最大冲击加速度随着率相关系数的增大而增大,其最大冲击加速度随率相关系数呈近似分段线性增长变化关系,当n<0.6时,变化较慢,当0.6 参 考 文 献 [1]王博. 正交各向异性蜂窝材料多功能优化设计[J]. 复合材料学报, 2008, 25(3):202-209. WANG Bo. Optimum design of multi-functional orthotropic honeycomb materials[J]. Acta Materiae Compositae Sinica, 2008, 25(3):202-209. [2]Wei Z, Zok F W, Evans A G. Design of sandwich panels with prismatic cores[J]. Journal of Engineering Materials and Technology, 2006, 128(2): 186-192. [3]沈伋, 李为吉. 蜂窝夹芯结构的电磁、重量多目标优化设计[J]. 西北工业大学学报, 1999, 17(4): 665-670. SHEN Ji, LI Wei-ji. Multi objective optimum design of honeycomb sandwich composite structure with electromagnetism and weight requirements[J]. Journal of Northwestern Polytechnical University, 1999, 17(4): 665-670. [4]张永存, 刘书田. 金属蜂窝材料换热性能分析快速数值算法[J]. 复合材料学报, 2008, 25(3): 197-201. ZHANG Yong-cun, LIU Shu-tian. Fast numerical algorithm for heat transfer efficiency of metallic honeycomb materials[J]. Acta Materiae Compositae Sinica, 2008, 25(3):197-201. [5]Gibson L J, Ashby M F. Cellular Solids: Structure and Properties[M]. 2nd ed. Cambridge: Cambridge University Press, 1997. [6]马连华,王亲猛,杨庆生. 不规则蜂窝夹芯面内等效弹性参数研究[R]. 第十五届全国复合材料学术会议, 2008, (7):946-950. [7]翟光, 杨小平. 多夹心层蜂窝板动力学特性分析与仿真[J]. 计算机仿真, 2006,23(8):44-45,85. ZHAI Guang, YANG Xiao-ping. Dynamic analysis and simulation of multi-inter layer honeycomb plate[J]. Computer Simulation, 2006,23(8):44-45,85. [8]王闯, 刘荣强, 邓宗全, 等. 铝蜂窝结构的冲击动力学性能的试验及数值研究[J]. 振动与冲击, 2008, 27(11): 56-61. WANG Chuang, LIU Rong-qiang, DENG Zong-quan, et al. Experimental and numerical studies on aluminum honeycomb structure with various cell specifications under impact loading[J]. Journal of Vibration and Shock, 2008, 27(11): 56-61. [9]Foo C C, Chai G B, Seah L K. A model to predict low-velocity impact response and damage in sandwich composites[J]. Composites Science and Technology, 2008, 68:1348-1356. [10]XUE Z Y, Hutchinson J W. Crush dynamics of square honeycomb sandwich cores[J]. International Journal for Numerical Methods in Engineering, 2006, 65: 2221-2245. [11]Tagarielli V L, Deshpande V S, Fleck N A, et al. A constitutive model for transversely isotropic foams and its application to the indentation of balsa wood[J]. International Journal of Mechanical Sciences, 2005, 47(425):666-686. [12]寇玉亮, 陈常青, 卢天健. 泡沫铝率相关本构模型及其在三明治夹芯板冲击吸能特性的应用研究[J]. 固体力学学报, 2011, 32(3):217-226. KOU Yu-liang, CHEN Chang-qing, LU Tian-jian. A rate-dependent constitutive model for aluminum foams and its application to the energy absorption of lightweight sandwich panels with aluminum foam cores[J]. Chinese Journal of Solid Mechanics, 2011, 32(3):217-226. [13]Wu E, Jiang W S, Axial crush of metallic honeycombs[J]. International Journal of Impact Engineering, 1997, 19(5):439-456. [14]胡金萍. 蜂窝夹心板动态力学行为研究[D]. 哈尔滨:哈尔滨工程大学, 2010. [15]刘耀东. 多孔金属材料率效应的数值分析与动态压缩行为的理论研究[D]. 合肥:中国科学技术大学, 2010. [16]Xu S Q, Beynon J H, Ruan D, et al. Experimental study of the out-of-plane dynamic compression of hexagonal honeycombs[J]. Composite Structures, 2012, 94:2326-2336.
