一端开口圆筒形爆室线状装药爆炸冲击波峰值压力计算分析
2014-09-05王朝成任辉启穆朝民王海露
王朝成,任辉启,穆朝民,王海露
(1.安徽理工大学,安徽 淮南 232001;2.中国科学技术大学 近代力学系,合肥 230027;3.总参工程兵科研三所,河南 洛阳 471023)
1 研究背景
爆炸模拟装置是模拟常规武器爆炸冲击波破坏效应的重要设备,对于研究爆炸冲击波对结构的冲击效应具有十分重要的意义。作为爆炸模拟装置的重要组成部分的爆室要在瞬间承受爆炸产生强冲击载荷的作用,因此研究柱状装药条件下爆室内的冲击波压力计算模型对于爆室强度的设计显得尤为重要。从90年代起,朱文辉[1]、钟方平[2]、张亚军[3]、穆朝民[4-5]等陆续对容器内部爆炸流场的分布和演变开展了相关的研究;白晓征等[6]对爆炸驱动管中柱状装药内爆轰波的传播过程进行了研究;刘君等[7]对爆炸波在爆炸模拟装置形成的二维和三维干扰流场进行了数值模拟;饶国宁等[8-9]对爆炸容器内部爆炸进行了数值模拟并对密闭空间内不同炸药爆源的能量输出结构及与目标作用进行了研究,以上研究对于爆炸容器内部爆炸波流场和爆炸容器的动态响应的研究起到了很好的促进作用,而对于一端开口一端封闭的圆筒形爆室线状装药爆炸冲击压力理论模型的研究尚不多见。
2 线状装药爆炸冲击波简化计算模型
将导爆索看成线状直列装药,爆炸产生的爆轰波沿线状装药传播,由于导爆索的爆速约为7 000 m/s,因而爆室内装药爆炸反应时间是ms量级,故可以假设线状装药是在瞬时完成爆轰的,则爆炸冲击波阵面的运动规律可以用CeДOB的自模拟解来描述:
(1)
式中:ρ0为未扰动大气密度,ri为冲击波阵面距离圆筒中轴线的距离,t为到达时间。
(2)
式中:E0为单位长度爆炸能量,λi为无量纲常数,由试验确定。
设线状装药长度为l,把线状直列装药分成相等的小段,其长度为Δl(见图1)。假设每小段装药是瞬时爆轰的,每小段装药末端的方向上的爆炸能量不会扩散,后一段装药从前一段爆炸时起经过时间Δt以后爆炸,Δt由下式求出:
(3)
式中:D0为装药的爆轰速度,它与装药密度有关,对于给定的炸药,这个速度是不变的。

图1 爆轰波沿柱状装药传播简图
根据上面的假设,柱状爆炸冲击波阵面的运动规律可以用式(1)来描述,其中时间t应按下式确定:
(4)
如果让研究的线状装药总长度l不变,使每小段Δl→0,即n→∞时,则每小段变成一个点,于是在图1上可用一条爆炸冲击波阵面位置的光滑曲线代替阶梯图形,这样,图1上的曲线就可以用式(1)和式(4)来确定。因此,考虑线状装药长度和炸药爆轰影响的冲击波阵面运动方程
(5)
线状装药爆轰完毕后,由于爆炸产物高温迅速膨胀,压缩周围空气,产生强烈的空气冲击波。用量纲理论来分析冲击波阵面的运动规律,在考虑周围介质压力P0=const≠0和密度ρ0=const≠0的情况下,可以给出爆炸力学特征待定参数组:ri,E0,p0,ρ0,t0。从上述参数组所包括的5个量中,可以组成2个独立无量纲组合:
(6)
因此,可得到冲击波阵面运动的函数关系式:
由试验结果可知,上述关系式为指数形式:
即
(7)
由式(7)可得到确定无量纲的表示式:
(8)
式中:E0=QQ0,Q0=0.42×106J/kg=106cal/kg=0.427×106kg·m/kg为单位质量爆炸能量,Q为单位长度上的装药量(kg/m),ρ0=0.131 5 kg·sec2/m4(20℃时的空气密度),p0=10 332 kg/m2。
试验表明1 kg线状直列装药空中爆炸时:
将上述数据代入式(8),计算得到λi=0.493 7,于是,式(7)可以改写成以下形式:
ri=A0t7/13
(9)
(10)
由式(9)可得到冲击波半径ri方向运动速度:
(11)
实际上,上述速度Di为每小段柱状装药爆炸冲击波运动速度,而长度l的线状装药爆炸冲击波的真实运动速度D应是冲击波阵面法线方向上的速度,即Di在法线方向上的投影(见图2)。

图2 冲击波真实速度
(12)
式中:α为法线n和半径ri的夹角。
由图2上的几何关系可知:
(13)
由式(5)和式(9)可得:
(14)
(15)
因此
(16)
(17)
将式(15)代入式(13)得:
(18)
将式(11)和式(18)代入式(12)便得到冲击波的真实速度:
(19)
将式(19)代入强冲击波阵面上的三个守恒关系式,化简后得到波阵面压力pi,波阵面质点速度ui和波阵面空气密度ρi:
(20)
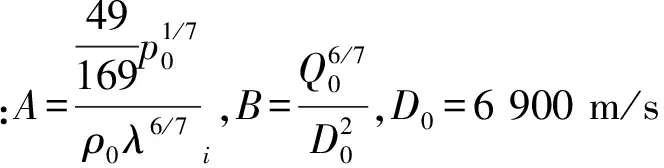
由上述数据计算出A=15.2,B=0.001 76。将这些数据代入式(20)中,可以获得计算冲击波阵面参数公式:
(21)
当线状装药在爆室中爆炸时,产生的空气冲击波被限制在爆室中运动,这时卷入运动的空气要比无限介质中爆炸少得多。设爆室平行轴线的截面面积为Ac,装药轴线长为l,ri为冲击波到装药轴线的距离即爆室半径(ri 将上式代入式(21),可得到爆室中线状装药爆炸时入射冲击波超压计算公式: (22) 式中:p0=0.103 32 MPa,适用条件为ri 入射冲击波与壁面相发生冲击波的反射,由于传感器安装在壁面的中央,故测得的冲击波超压为正反射超压。第一个脉冲尖峰为正反射最大超压,可以用正反射超压公式计算: (23) 式中:Δpi为入射冲击波超压,由式(22)计算。 爆室内半径r=500 mm,长l=1 600 mm,开口处半径rc=250 mm如图3所示,在垂直于炸药上方的爆室壁面安放压力传感器。用法兰对爆室两端进行固定。压力传感器的量程为5.0 MPa,固有频率300 kHz,最大灵敏度20 mV/psi,上升时间小于2 μs,低频响应0.005 Hz。测压时,把压力传感器拧入爆室测压孔内,传感器测压面与爆室壁面平齐。 图3 试验装置示意图 图4 实测波形 计算结果与实测值的比较见表1,第5炮和第6炮实测波形如图4所示,可以看出,计算值与实测值吻合较好,说明本文提出的简化计算方法基本反映实际情况。 表1 入射超压与反射超压计算值与实测的比较 通过理论推导建立了线状装药在一端开口爆室中心爆炸时,空气冲击波压力的计算模型,该模型考虑了线状装药长度和爆轰波速度及圆筒内壁反射作用对爆炸流场基本参数的影响,并利用计算模型对爆室内线状装药爆炸压力进行了分析计算,计算结果与实测数据吻合较好。 [1]朱文辉,薛鸿陆,刘仓理,等.爆炸容器承受内部加载的实验研究[J].爆炸与冲击,1995,15(4):374-375. ZHU Wen-hui.XUE Hong-lu,LIU Cang-li,et al.Experimental study on the explosive chambers under internal blast loading[J].Explosion and Shock Waves,1995,15(4):374-375. [2]张亚军,张梦萍,徐胜利,等.爆炸容器内冲击波系演化及壳体响应的数值研究[J].爆炸与冲击,2003,23(4):331-336. ZHANG Ya-jun,ZHANG Meng-pin,XU Sheng-li,et al.Numerical investigation on blast wave propagation and dynamic response of an explosion vessel[J].Explosion and Shock Waves,2003,23(4):331-336. [3]钟方平,陈春毅,林俊德,等.双层圆柱形爆炸容器弹塑性结构响应的实验研究[J].兵工学报,2000,21(3):268-271. ZHOGN Fang-pin,CHEN Chun-yi,LIN Jun-de,et al.An experimental study on the elasto-plastic response of double-walled cylindrical explosion containment vessel[J].Acta Armamentarll,2000,21(3):268-271. [4]穆朝民,任辉启,李永池,等.爆室内爆炸流场演化与壳体动力响应的数值模拟[J].弹箭与制导学报,2010,30(2):82-86. MU Chao-min,REN Hui-qi,LI Yong-chi,et al.Numerical simulation on blast flow field evolution and dynamic response of blast chamber [J].Journal of Projectiles,Rockets,Missiles and Guidance,2010,30(2):82-86. [5]穆朝民,任辉启,李永池,等.爆室内爆炸流场演化与壳体动力响应研究[J].振动与冲击,2009,28(10):106-111. MU Chao-min,REN Hui-qi,LI Yong-chi,et al.Blast flow field evolution and dynam ic response of a blast chamber[J].Journal of Vibration and Shock,2009,28(10):106-111. [6]白晓征,刘瑞朝,刘君.驱动管中柱状装药爆轰过程的数值模拟[J].国防科技大学学报,2009,30(5):106-111. BAI Xiao-zheng,LIU Rui-chao,LIU Jun.Numerical simulation of detonation in cylindrical Eexplosives in driving Tube[J].Journal of National University of Defense Technology,2009,30(5):106-111. [7]刘君,刘瑞朝,贾忠湖,等.爆炸波与物体干扰流场的数值模拟[J].空气动力学学报,2000,18(1):55-61. LIU Jun,LIU Rui-chao,JIA Zhong-hu,et al.Numerical simulation of blast interaction with building[J].Acta Aerodynamica Sinica,2000,18(1):55-61. [8]饶国宁,陈网桦,梁德山,等.爆炸容器内部爆炸的数值模拟和实验研究[J].弹道学报,2008,20(1):76-80. RAO Guo-ning,CHEN Wang-hua,LIANG De-shan,et al.Numerical and experimental study on internal blast in explosion chamber[J].Journal of Ballistics,2008,20(1): 76-80. [9]饶国宁,陈网桦,梁德山,等.密闭空间内不同炸药爆源的能量输出结构及与目标作用研究[J].爆炸与冲击,2007,27(5):445-450. RAO Guo-ning,CHEN Wang-hua,LIANG De-shan,et al.Study on the energy output characteristics and action with objects of different explosives in the confined field[J].Explosion and Shock Waves,2007,27(5):445-450.3 线状装药爆炸冲击波压力的实验研究



4 结 论
