临界接触参数连续的粗糙表面法向接触刚度弹塑性分形模型

王南山，张学良，兰国生，温淑花，陈永会，刘丽琴，牛作证

(太原科技大学 机械工程学院,太原 030024)

由零件、组件、部件之间相互联接的粗糙接触表面即为结合面,机器或机械结构大量存在着各种各样的结合面。结合面属于“柔性结合”,其既存储能量又消耗能量,表现出既有弹性又有阻尼,即存在接触刚度和接触阻尼[1]。结合面的接触刚度常常是机械结构整体刚度的重要组成部分,有时甚至成为整体刚度的薄弱环节；对于行业重要设备机床而言,其结合面的接触刚度约占机床总刚度的60%～80%,对不同的机床,这个比例的具体值也不尽相同[1-2]。

粗糙表面形貌对结合面接触刚度有重要的影响,而结合面的接触刚度在机械结构静动态特性中(占显著地位[3]。接触界面的存在导致组合结构局部刚度降低,直接影响结构的机械性能。为准确进行组合结构的动力分析,必须获得粗糙表面的接触刚度[4]。接触刚度的确定是许多工程结构在振动分析中常遇到的问题,如拉杆转子各叶轮轮盘间的接触刚度[5],机床导轨与工作台之间的接触刚度等[6]。在对装配体进行模态分析时,装配体接触面间的法向接触刚度对计算结果具有很大影响[7]。

文献[1,3-11]对粗糙表面的接触刚度的进行了相应的研究,但主要基于弹性和塑性变形机制下进行的。文献[12-18]对粗糙表面的接触机制进行了相关研究,并且均指出把结合面的接触机制考虑为单一的完全弹性或完全塑性变形以及同时考虑弹性和塑性变形的情况时均存在着一定的缺陷,结合面的接触需要经历弹性、弹塑性、塑性变形的三种变形机制,但并未给出临界点处接触参数连续的弹塑性分形接触刚度模型。本文基于接触分形理论及其修正模型,改善接触临界点处接触参数不连续情况,建立了计及微接触面积分布的域扩展因子影响的结合面法向接触刚度弹塑性分形模型。数值仿真揭示了弹塑性过渡变形机制及相关参数对结合面法向接触刚度的影响。

1 结合面接触理论建模

1.1 接触变形机制

结合面是由两个粗糙表面接触形成,两粗糙表面的接触实质为分布于两接触表面上的微凸体间的相互作用；通常将两粗糙表面的接触简化为一粗糙表面和一刚性平面的接触,对于粗糙表面的单个微凸体,将其等效为半球体,其等效曲率半径为R,如图1(a)所示。当在法向预加载荷p作用下,接触区域半径为r,法向变形为δ,如图1(b)所示。

1.1.1 完全弹性变形机制

当微凸体的变形在弹性范围内时,即根据赫兹接触理论,单个微凸体法向接触载荷[9,18-19]

(1)

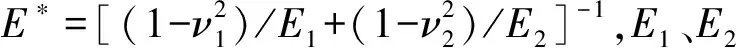
1.1.2 完全塑性变形机制

当微凸体法向变形量进入完全塑性变形范围,即δ≥76.4δc时[20](δc为微凸体由完全弹性变形进入弹塑性过渡变形阶段的临界变形量),微凸体将处于完全塑性变形机制,此时接触载荷可表示为[18]

pp=2HπRδ

(2)

而从完全弹性变形进入弹塑性过渡变形阶段的的临界变形量δc为[13,18]:

(3)

式中：H为软材料的硬度(H=2.8Y,Y为软材料的屈服强度),K为硬度系数,其值与软材料的泊松比有关，K=0.454+0.41ν。

1.1.3 弹塑性过渡变形机制

当微凸体的变形量位于δc≤δ≤76.4δc范围时,即处于弹塑性过渡变形阶段；此阶段的接触载荷为[20]

(4)

1.2 弹塑性接触参数的分形模型

实际工程表面并非理想的平面,其上总是分布着无数的微凸体,所有微凸体相互作用的接触面积之和为结合面的真实接触面积,真实接触面积往往远小于名义接触面积。为了能够更准确地表达结合面最大微接触点的实际接触面积al与粗糙表面的真实接触面积Ar之比al/Ar,Wang等[21]在MB分形模型基础上引入了微接触点大小分布域扩展因子ψ,给出了微接触截面积为a′的接触点大小的分布函数为

(5)

图2 当量粗糙表面1与理想刚性表面2的接触

根据文献[10-11、21]微凸体顶端的变形量δ、微凸体的曲率半径R分别可表示为:

(6)

(7)

式中:G为分形粗糙度参数;γ为大于1的常数,对于服从正态分布的随机表面,γ=1.5较符合高频密度和相位随机的情况。

由式(3)、式(6)、式(7)可得

(8)

1.2.1 接触面积

结合面的真实接触面积应为完全弹性真实接触面积、完全塑性真实接触面积、弹塑性真实接触面之和,即为

(9)

将式(5)代入式(9)有

(10)

1.2.2 接触载荷

整个结合面上的法向接触载荷应为完全弹性接触载荷、塑性接触载荷、弹塑性接触载荷之和。

结合面上完全弹性接触载荷可表达为

(11)

将式(1)、(5)～(7)代入式(11)可得：

(12)

同理可得：

结合面上完全塑性接触载荷为

(13)

结合面上弹塑性接触载荷为

(14)

则整个结合面上的法向接触载荷可表示为

P=Pp+Pep+Pe

(15)

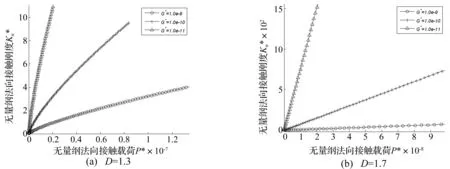
将式(12)～(14)代入式(15),则当1

(D≠1.5)

(16)

(D=1.5)

(17)

根据弹性接触点的实际接触面积a与截断面积a′之间的关系[17]

a′=2a

(18)

可以得出如下关系

(19)

(20)

将式(19)、(20)分别代入式(16)、(17),并对(16)、(17)进行无量纲化处理,则有

(D≠1.5)

(21)

(D=1.5)

(22)

2 结合面法向接触刚度弹塑性分形模型

当结合面上的微凸体法向变形量δ≥76.4δc时,将处于完全塑性变形范围,即当接触机制处于弹性和弹塑性阶段时存在法向接触刚度。

对于单个微凸体,根据文献[23]可得：

完全弹性阶段的法向接触刚度

(23)

弹塑性阶段的法向接触刚度

(24)

将式(7)、(8)代入式(24)则有

(25)

则整个结合面的法向接触刚度为

(26)

将式(9)、(23)、(25)代入式(26)则有

(27)

将式(27)无量纲化处理

(28)

式中：

至此,建立了临界接触参数连续条件下的法向刚度弹塑性的分形模型；由(21)、(22)、(28)可以看出,数学模型表明了无量纲法向接触刚度、结合面分形参数以及结合面材料特性参数之间的复杂非线性关系。

3 结合面法向接触刚度弹塑性分形模型数值仿真

3.1 数值仿真

图3 无量纲法向接触刚度随无量纲法向接触总载荷P*的变化规律以及分形维数D对无量纲法向接触刚度的影响(G*=1.0E-10,φ=1.5)

图4 分形粗糙度G*对无量纲法向接触刚度的影响(φ=1.5)

图5 塑性指数φ对无量纲法向接触刚度的影响(G*=1.0E-10)

3.2 仿真结果分析

(2)结合图3(a)、(b)可以看出,当分形维数D=1.1～1.5时,无量纲法向接触刚度随着分形维数D的增大而增大；而当分形维数D=1.5～1.9时,无量纲法向接触刚度随着分形维数D的增大而减小,这一点与文献[3、10]结果有所差异,主要原因在于弹塑性过渡变形机制的引入。

(3)根据图3(a)、(b)无量纲法向接触刚度随无量纲法向接触总载荷的变化情况以及分形维数对于无量纲法向接触刚度的影响,分别选取两代表性的分形维数取值D=1.3、1.7,并对无量纲分形粗糙度G*和塑性指数φ对无量纲法向接触刚度的影响进行了仿真分析。无量纲法向接触刚度随着分形粗糙度G*的增大而减小,如图4(a)、(b)所示；无量纲法向接触刚度随着塑性指数G*的增大而增大,如图5(a)、(b)所示；这与文献文献[3、10]结果一致。

4 结 论

(1)建立了临界接触参数连续条件下计及微接触面积分布域扩展因子影响的结合面法向接触刚度弹塑性分形模型。

(2)数据仿真表明弹塑性过渡变形机制对法向接触刚度影响明显；且弹塑性过渡变形机制下的法向接触刚度大于仅考虑弹性和塑性接触机制下对应的法向接触刚度,这将有助于得到精确的机械结构接触刚度模型,从而提高动力学分析的准确性,对机械结构的静动态特性进行更为准确的分析。

(3)无量纲法向接触刚度随着无量纲法向接触载荷的增大而增大且因分形维数取值不同而呈凸弧性的非线性关系或近似线性关系,随着分形维数增大而增大(分形维数D=1.1～1.5)或者减小(分形维数D=1.5～1.9)；随着分形粗糙度的增大而减小；随着塑性指数的增大而增大。

[1]张学良.机械结合面动态特性及应用[M].北京:中国科技技术出版社,2002:1-2.

[2]Burdekin M，Back N，Cowley A.Analysis of the local deformation in machine joints [J].Journal of Mechanical Engineering Science,1979,21(1): 25-32.

[3]温淑花,张学良,武美先,等.结合面法向接触刚度分形模型及其仿真[J].农业机械学报,2009，40(11):197-202.

WEN Shu-hua，ZHANG Xue-liang，WU Mei-xian，et al.Fractal model of normal contact stiffness of joint interfaces and its simulation[J].Transactions of the Chinese Society for Agricultural Machinery，2009,40(11):197-202.

[4]李辉光,刘恒,虞烈.粗糙机械结合面的接触刚度研究[J],西安交通大学学报2011,45(6):69-74.

LI Hui-guang，LIU Heng,YU Lie.Contact stiffness of rough mechanical joint surface[J].Journal of Xi’an Jiaotong University，2011，45(6): 69-74.

[5]李辉光,刘恒,虞烈.考虑接触刚度的燃气轮机拉杆转子动力特性研究[J].振动与冲击，2012,31(7):4-8.

LI Hui-guang，LIU Heng，YU Lie.Dynamic characteristics of rod fastening rotor for gas turbine considering contact stiffness[J].Journal of Vibration and Shock，2012,31(7):4-8.

[6]饶柱石,夏松波,汪光明.粗糙平面接触刚度的研究[J].机械强度,1994,16(2):72-75.

RAO Zhu-shi，XIA Song-bo，WANG Guang-ming.A study of contact stiffness of flat rough surfaces[J].Journal of Mechanical Strength,1994，16(02):71-75.

[7]艾延廷，翟学,王志,等.法向接触刚度对装配体振动模态影响的研究[J].振动与冲击，2012，31(6):171-174.

AI Yan-ting，ZHAI Xue，WANG Zhi,et al.Influences of normal contact stiffness on an assembly’s vibration models[J].Journal of Vibration and Shock,2012,31(6):171-174.

[8]刘意,刘恒,易均,等.计及塑性接触层的法向接触刚度等效方法[J].振动与冲击,2013,32(7):43-47.

LIU Yi，LIU Heng,YI Jun,et al.Equivalent method for normal contact stiffness considering plastic contact layer[J].Journal of Vibration and Shock,2013,32(7):43-47.

[9]张学良,黄玉美,韩颖.基于接触分形理论的机械结合面法向接触刚度模型[J].中国机械工程,2000,11(7): 727-729.

ZHANG Xue-liang，HUANG Yu-mei，HAN Ying.Fractal model of the normal contact stiffness of machine joint surfaces based on the fractal contact theory[J].China Mechanical Engineering，2000,11(7):727-729.

[10]兰国生,张学良,丁红钦,等.基于分形理论的结合面改进模型[J].农业机械学报,2011,42(10):217-223.

LAN Guo-sheng，ZHANG Xue-liang，DING Hong-qin,et al.Modified contact model of joint interfaces based on fractal theory[J].Transactions of the Chinese Society for Agricultural Machinery,2011,42(10):217-223.

[11]Jiang Shu-yun，Zheng Yun-jian.A contact stiffness model of machined joint surfaces[J].Journal of Tribology，Transactions of ASME，2010 ,132(1):1-7.

[12]尤晋闽,陈天宁.结合面静态接触参数的统计模型研究[J].振动与冲击，2010,29(11):47-50.

YOU Jin-min，CHEN Tian-ning，Statisticalmodel for static contact parameters of joint surfaces[J].Journal of Vibration and Shock，2010,29(11):47-50.

[13]Kogut L，Etsion I.Elastic-plastic contact analysis of a sphere and a rigid flat [J].ASME J.Appl.Mech,2002,69:657-662.

[14]Lin L P，Lin J F.An elastoplastic microasperity contact model for metallic materials[J].ASME J.Tribol，2005，127:666-672.

[15]Jackson R L，Green I.A finite element study of elastoplastic hemispherical contact against a rigid flat[J].ASME J.Tribol，2005,127:343-354.

[16]Chung J C，Lin J F.Variation in fractal properties and Non-Gaussian distributions of microcontact between elastic-plastic rough surfaces with mean surface separation[J].ASME J.Appl.Mech.，2006，73:143-152.

[17]赵永武,吕彦明,蒋建忠.新的粗糙表面弹塑性接触模型[J].机械工程学报,2007,43(3):95-101.

ZHAO Yong-wu，LÜ Yan-ming，JIANG Jian-zhong.New elastic-plastic model for the contact of rough surfaces[J].Chinese Journal of Mechanical Engineering.2007，43(3):95-101.

[18]尤晋闽,陈天宁.结合面法向动态参数的分形模型[J].西安交通大学学报,2009,43(9):91-94.

YOU Jin-min，CHEN Tian-ning.Fractal model for normal dynamic parameters of joint surfaces[J].Journal of Xi’an Jiao Tong University，2009,43 (9):91-94.

[19]Johnson K L.Contact mechanics[M].Cambridge: Cambridge university press，1985.

[20]Liou J L.The theoretical study for microcontact model with variable topography parameters[D].Tiwan:National Cheng Kung University,2006.

[21]Wang S，Komvopoulosk K.A fractal theory of the interfacial temperature distribution in the slow sliding Regime:part I-elastic contact and heat transfer analysis[J].Trans.of ASME J.Tribol,1994,116(4):812-823.

[22]田红亮,赵春华,朱大林,等.金属材料结合部法切向刚度修正与实验验证[J].农业机械学报,2012,43(6):207-214.

TIAN Hong-liang，ZHAO Chun-hua，ZHU Da-lin,et al.Modification of normal and tangential stiffness for joint interface with metallic material and experimental validation[J].Transactions of the Chinese Society for Agricultural Machinery,2012，43(6):207-214.

[23]ZhaoY，Maietta D M，Chang L.An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow[J].ASME Journal of Tribology，2000，122: 86-93.