变刚度橡胶球铰的刚度特性与疲劳寿命分析

丁智平， 杨荣华， 黄友剑， 卜继玲

(1.湖南工业大学 机械工程学院，湖南 株洲 412007；2.株洲时代新材料科技股份有限公司，湖南 株洲 412007)

随着轨道交通的迅猛发展，对车辆安全性、舒适性、可靠性要求更高[1]。橡胶弹性减振元件可承受牵引、悬挂、隔振、缓冲作用，已被广泛用于轨道交通、高速车辆减振系统中[2]。而橡胶球铰具有柔性连接及减缓振动冲击作用，且不产生机械摩擦、无需润滑、噪声低、结构简单、无需维护等优点，成为轨道交通工程中广泛应用的弹性减振元件[3]。

工程上已用有限元对橡胶弹性减振元件的承载特性进行分析，但对其疲劳寿命预测，由于影响因素多、疲劳损伤机理复杂仍缺乏有效方法。目前对橡胶元件疲劳寿命的研究，主要有基于连续介质力学理论的裂纹萌生寿命分析方法与基于断裂力学理论的裂纹扩展寿命分析方法[4]。前者通过研究橡胶元件局部位置的应力、应变变化历程预测橡胶元件寿命；后者则通过研究橡胶元件局部位置微小裂纹扩展过程预测橡胶元件疲劳寿命。两种方法均有不足，较难设计合适的试验方法确定橡胶元件局部位置应力应变历程及微小裂纹扩展过程。Mars等[4-5]对橡胶材料的疲劳寿命进行过深入研究。Saintier等[6]以构型力学理论为基础，用哑铃型橡胶试样进行橡胶材料的多轴疲劳试验与分析，较准确地预测出橡胶材料承载单轴与多轴载荷时的疲劳失效位置，并提出新的疲劳评价参数。Kim等[7]以最大应变能密度、最大格林应变作为疲劳损伤参量对发动机橡胶悬置的疲劳寿命进行预测。Li 等[8]以最大对数主应变为损伤参量对橡胶悬置的单轴疲劳寿命进行研究。丁智平等[2]基于橡胶纯剪试样实验数据，以撕裂能范围为损伤参数，对橡胶锥形簧的疲劳寿命进行分析。王文涛等[9]基于线性疲劳累积损伤原理，提出张量形式橡胶疲劳寿命公式，通过试样疲劳试验，以最小二乘法原理拟合拉伸与剪切的疲劳寿命公式，对车用变速箱悬置与发动机后悬置的疲劳寿命进行预测研究。

牵引杆橡胶球铰作为牵引拉杆中的重要弹性元件，正常行驶工况下，为满足车辆舒适性，要求橡胶球铰具有较低的径向刚度，而在大转弯、急停等突发极限工况下又能具有较大刚度，以保证车辆行驶安全性与可靠性。本文对新型变刚度橡胶球铰刚度特性及疲劳寿命进行分析探讨。

1 变刚度橡胶球铰结构及工作特性

变刚度橡胶球铰在牵引杆系统中起传递牵引力作用(图1)，其基本结构由芯轴、外套、止挡及橡胶组成，见图2。变刚度橡胶球铰主要结构为：橡胶型面用开放式结构设计，有利于橡胶在承载时的应力释放，径向沿止挡方向有一能产生大刚度的变刚度内孔，垂直于止挡径向，采用完整型面设计以保证产品承载所需，承载性能见表1。

图1 牵引杆球铰

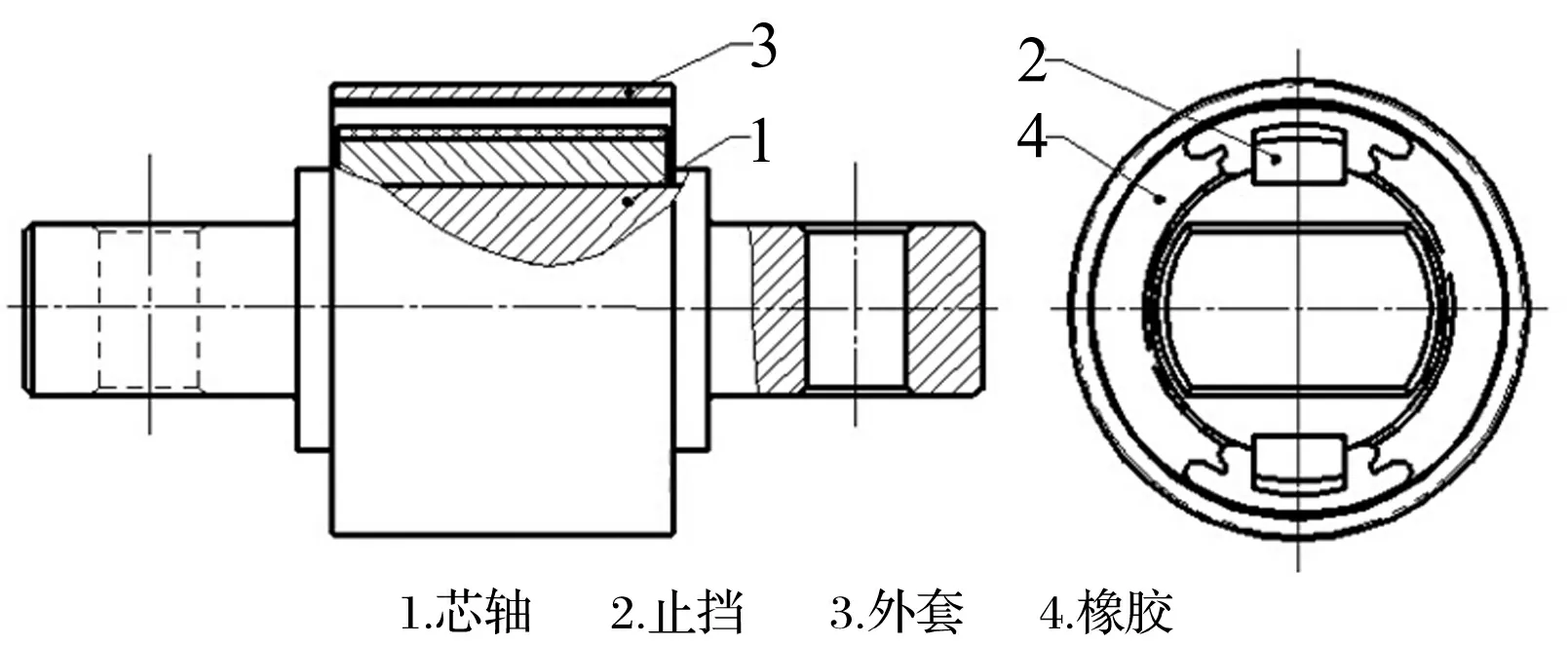
1.芯轴 2.止挡 3.外套 4.橡胶

由球铰结构与承载特点看出，该球铰主要承受径向载荷(沿止挡方向)。 正常工况时，止挡与外套间发生相对位移，并始终保有间距，不发生接触，刚度特性较平稳；大载荷工况时，止挡上部橡胶层与外套接触，限制二者间的相对位移，使橡胶球铰刚度特性发生显著改变。因此可据实际承载要求对球铰径向方向止挡高度进行调整，使之能用于不同工况的悬架系统，因而提高了产品的适用性。

表1 牵引杆球铰承载性能

2 变刚度橡胶球铰刚度特性

2.1 橡胶材料本构模型参数

常用的橡胶材料本构模型主要分为三类[10]：① 分子统计学理论本构模型；② 以应变不变量表示的应变能密度函数；③ 以主伸长率表示的应变能函数。为准确描述橡胶球铰橡胶材料的力学特性，委托美国Axel实验室进行橡胶材料单向拉伸、双向拉伸及平面拉伸等力学性能实验。利用实验数据对不同橡胶本构模型进行拟合，结果表明三阶Ogden本构模型与实验数据相关性最好，见图3。该模型以三个主伸长率λ1,λ2,λ3为变量表示应变能函数，表达式为[11]：

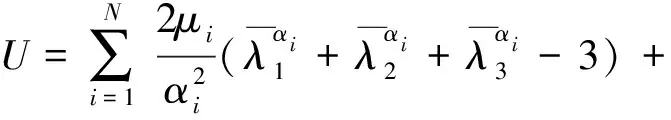
(1)

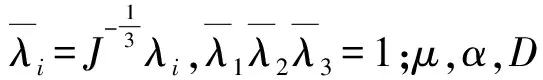
表2 橡胶材料本构模型参数

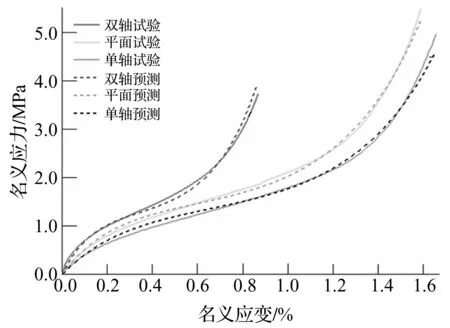
图3 Ogden 三阶模型拟合

2.2 刚度特性分析

为研究橡胶球铰的刚度特性，本文对橡胶球铰沿止挡方向刚度进行有限元数值模拟及实验测试。

2.2.1 有限元模型与载荷边界条件

为减少计算时间，考虑几何模型与载荷的对称性，取四分之一模型进行分析，在三维软件中建立实体模型并导入Hypermesh软件中进行前处理网格划分，并将划分的网格模型导入ABAQUS软件中分析计算，建立的有限元模型见图4。

图4 有限元分析模型

据所建有限元模型，考虑橡胶球铰实际工况的载荷与边界条件，在芯轴一端施加固定约束，沿XY平面与YZ平面施加对称约束，在外套沿Y方向施加载荷17.5 kN，载荷边界条件见图5。

2.2.2 分析与试验结果

用Ogden三阶模型对球铰刚度进行有限元分析，所得计算刚度与产品刚度试验结果见图6。正常工况与极限工况时计算静刚度及经试验所得静刚度值见表3。计算、测试结果表明，该球铰的变刚度特性符合实际工况承载要求，即在正常行驶工况载荷下具有较低的径向刚度，满足车辆舒适性要求；而在极限工况载荷下能提供大刚度以保证车辆的安全性。

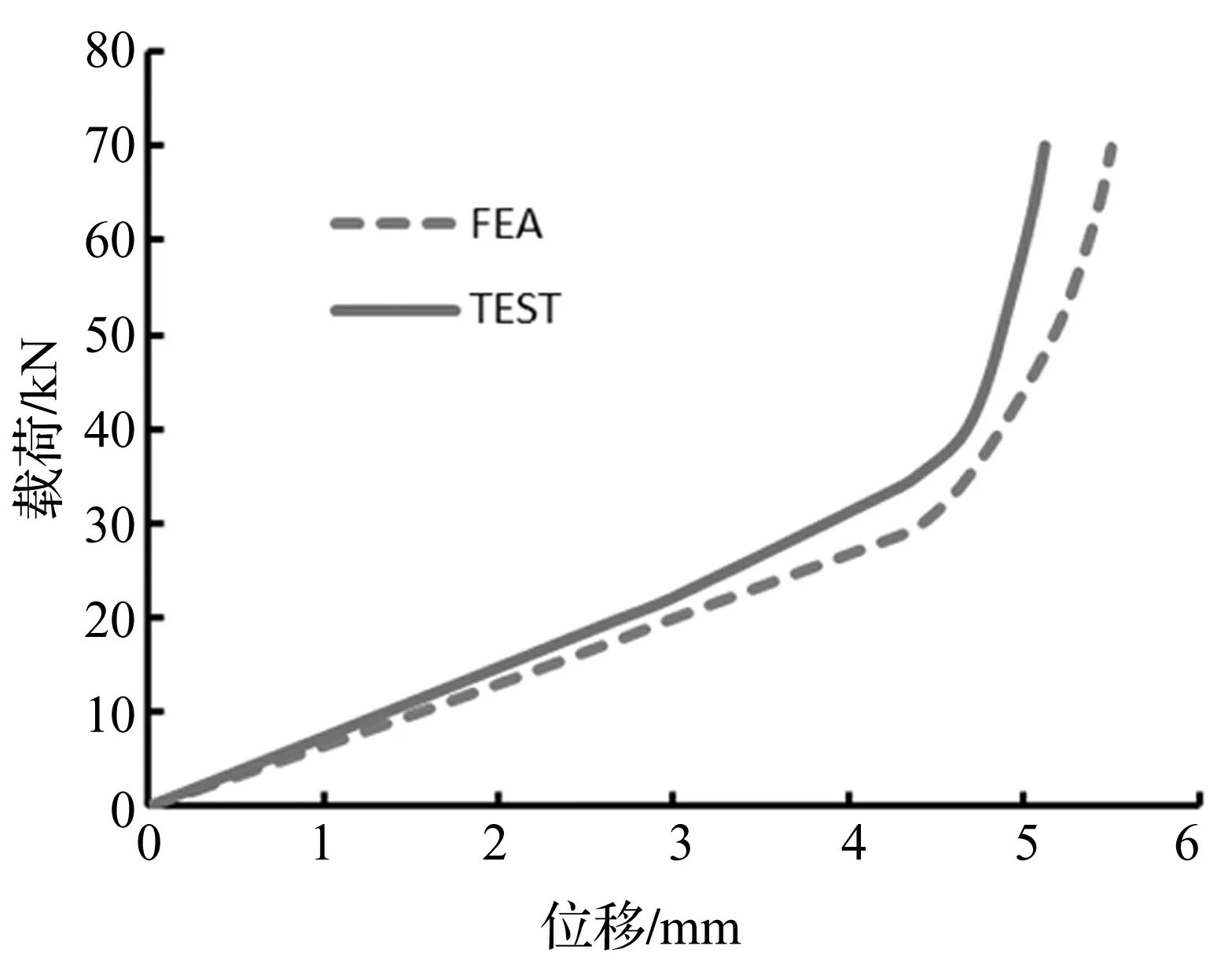
图6 静刚度有限元分析与测试结果

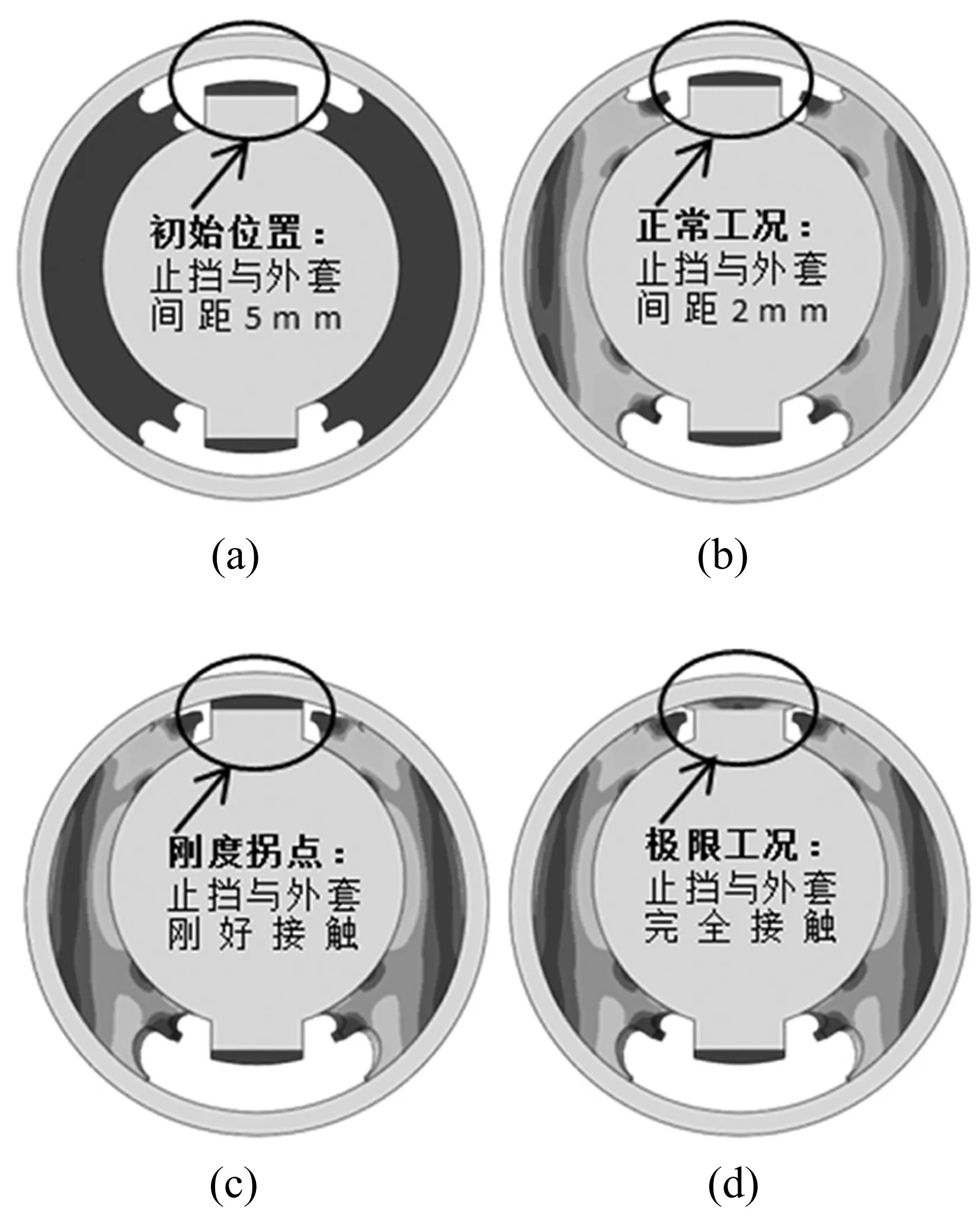
图7 不同载荷下橡胶球铰变形趋势

图7为橡胶球铰在不同工况下变形情况，反应出承载特性随载荷的变化过程。在图7(a)的初始位置，止挡与外套保持一定初始间距；图7(b)为正常工况下止挡与外套间距缩小，但二者未发生接触，橡胶球铰刚度特性较平稳；当球铰外套与止挡发生接触时(图7(c))，该橡胶球铰刚度特性随之发生显著变化，随载荷增大，刚度值不断增大，极限载荷下达到最大值(图7(d))。由橡胶球铰的工作原理知其刚度特性表现为非线性特征，正常工况下刚度值基本保持不变；当橡胶球铰外套与止挡发生接触时，刚度曲线出现拐点，随之刚度显著增大，可满足极限工况下的承载要求。因此，橡胶球铰刚度特性发生改变的位置与外套与止挡间距关系密切。本文对几种不同止挡高度的橡胶球铰刚度响应进行数值模拟，结果见图8。

表3 静刚度计算值与试验结果对比

图8 不同止挡高度时刚度曲线

由图8可知，通过调整止挡高度H0，可改变刚度曲线拐点，进而满足不同类型悬架系统的极限承载要求。该新型球铰的设计结构适用性良好。

3 变刚度橡胶球铰疲劳寿命分析

牵引杆橡胶球铰在实际工况下，橡胶部分区域往往处于复杂应力状态，仅用单一应力并不能准确评估其疲劳特性。而用等效应力结合橡胶材料S-N曲线则为预测橡胶材料疲劳寿命的有效方法[12-14]。据多种橡胶产品疲劳实验数据，获得橡胶疲劳寿命的S-N曲线见图9[15]。该S-N曲线主要有三个寿命评价基准，分别为100万次、300万次和500万次。图9中纵坐标Δσ为应力范围。

图9 橡胶材料S-N曲线

橡胶弹性元件在载荷作用下通常为大变形状态，与金属材料的小变形显著不同，因而不宜用Mises应力评估橡胶元件的疲劳性能，而应采用主应力或主应变为疲劳损伤参量预测其疲劳寿命。橡胶球铰的使用工况复杂，主要受压缩、剪切等大变形的周期载荷作用，其中拉应力与剪应力对橡胶疲劳寿命影响最大。对橡胶的超弹特性已有研究表明[16-18]，橡胶弹性元件在实际工况载荷的受力状态，可用含三个主应力值的等效应力表示，并作为预测橡胶疲劳寿命的损伤参量。等效应力σf计算式为[16]：

(2)

式中：σf为等效应力；σ1，σ2，σ3为三方向主应力。主应力须大于零，因为假设只有拉应力对橡胶裂纹扩展有贡献，而压应力使裂纹闭合，对裂纹扩展无贡献。

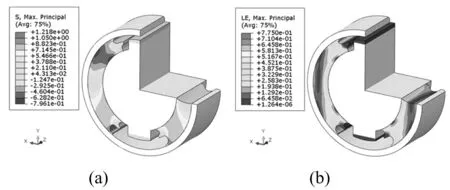
图10 30 kN疲劳载荷下橡胶应力应变分布

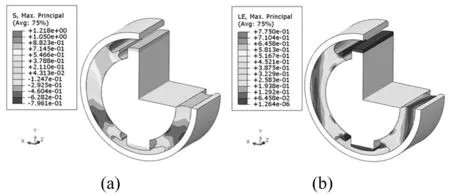
图11 -30 kN疲劳载荷下橡胶应力应变分布

通过循环加载有限元分析，获得橡胶球铰在疲劳载荷工况(-30～30 kN)时最大主应力、最大主对数应变分布见图10、图11。

由疲劳损伤理论知，疲劳损伤参量应为应力范围或应力幅值。由于主应力范围均大于零，在计算等效应力范围时A、B取1，等效应力范围计算式为：

(3)

式中：Δσ1,Δσ2,Δσ3为三个主应力范围。

据疲劳载荷工况，对橡胶球铰有限元模型施加一周期循环载荷，整个分析过程分四个载荷步，见图12。据最大主对数应变分布情况可确定危险区域，分别提取危险区域单元在±30 kN两种载荷的三方向主应力值，危险区域某一单元在一个周期载荷的三主应力时间历程曲线见图13。由式(3)计算的危险单元等效应力范围Δσf见表4，可见与Mises应力范围相差较大，说明Mises应力范围不适用大变形橡胶材料。由图13看出，危险区域在-30 kN时三方向主应力均为负值，表明承受压应力；而在+30 kN时主应力均为正值，表明承受拉应力。

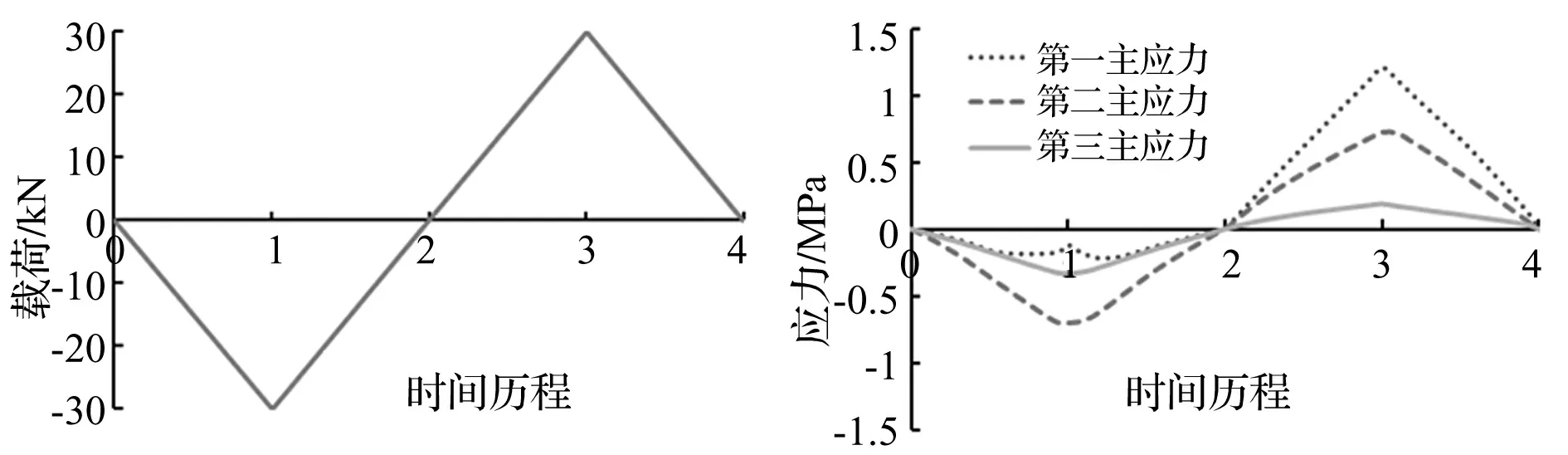
图12 有限元分析载荷步

表4 危险区域单元等效应力范围

由表4看出，等效应力范围Δσf的最大值为2.264 MPa，利用图9橡胶材料S-N曲线进行插值计算获得疲劳寿命约为170万次。图10的有限元分析结果显示球铰橡胶最大主对数应变值为77.5%。据工程设计规范[9]，橡胶球铰疲劳寿命为150万次循环，最大主对数应变应控制在80%以下，因此满足设计规范要求。

4 橡胶球铰刚度测试与疲劳试验

4.1 试验内容

橡胶球铰在使用过程中须同时满足刚度匹配及疲劳寿命要求。因而产品试验应包括径向(止挡方向)刚度测试及疲劳寿命试验。刚度测试时，支撑球铰两端芯轴在球铰中间位置施加载荷，以58 kN/min的加载速度从0到70 kN预加载三次，卸载后3～5 min开始测试。分别测试0～30 kN载荷区间(正常工况)静刚度与50～70 kN载荷区间(极限工况)静刚度。

图14 橡胶球铰疲劳试验

产品疲劳试验条件为：径向动态载荷±30 kN，环境温度在23±2℃内，采用正弦波加载，频率2 Hz。试验中对球铰橡胶表面温度进行监测，每次监测间隔时间不超过1 h，当温度高于40℃时调低试验频率或短时停机。疲劳次数达150万次时，若球铰的金属与橡胶间或橡胶表面出现裂纹，深度不超5 mm、长度不大于球铰橡胶圈周长的1/3，且刚度变化率不超球铰初始刚度的25%，则视为合格。橡胶球铰台架疲劳试验见图14。

4.2 试验结果验证

橡胶球铰产品完成150万次疲劳试验后，未发现超设计规范裂纹，见图15。在23℃恒温下放置24 h后检测径向刚度，正常工况的静刚度为6.8 kN/mm，极限工况静刚度为13.6 kN/mm，试验结果见表5。疲劳试验前后正常工况与极限工况径向刚度变化率分别为8.1%，4.9%，产品满足设计要求。

图15 产品疲劳试验后

表5 疲劳试验前后静刚度

5 结 论

(1) 有限元分析与实验研究表明变刚度橡胶球铰刚度特性非线性明显。正常工况载荷时刚度响应较平稳；极限工况时刚度显著增大，有限元数值模拟与实验所得刚度值偏差为10.8%，11.2%。

(2) 刚度曲线变化拐点位置随球铰止挡高度不同而变化，止挡高度增加，拐点位置沿刚度曲线前移，反之则后移。通过调整止挡高度可改变承载特性，满足不同悬架系统的承载要求。

(3) 据橡胶的超弹特性，通过循环加载有限元分析，计算疲劳工况载荷时球铰危险部位等效应力范围，并结合S-N曲线预测其疲劳寿命为170万次。橡胶球铰经台架疲劳实验150万次后未发现超设计规范裂纹，与寿命预测值基本吻合，疲劳试验前后径向刚度变化率分别为8.1%，4.9%，满足产品设计要求。

中国教师：您曾说过会努力实现教育资源均衡、公平。好学校、好校长、好教师、好学生和好的教育生态已成为广州办好教育、实现均衡的5个重要抓手，所以也有的人说您是这“五好教育”的倡导者。在这几个方面，您有哪些特别有感触的地方？

参 考 文 献

[1]王 进,彭立群,侯海彪,等.轨道交通用橡胶关节的结构与特性[J].世界橡胶工业,2006(8): 23-26.

WANG Jin, PENG Li-qun,HOU Hai-biao, et al. The structure and character of bushing used for railways[J]. Journal of World Rubber Industry, 2006(8):23-26.

[2]丁智平,陈吉平,宋传江,等.橡胶弹性减振元件疲劳裂纹扩展寿命分析[J].机械工程学报,2010,46(22):58-64.

DING Zhi-ping, CHEN Ji-ping, SONG Chuan-jiang, et al. Analysis of fatigue crack growth life for rubber vibration damper[J].Journal of Mechanical Engineering, 2010, 46(22): 58-64.

[3]彭立群,林达文,王 进,等.铁道车辆用橡胶球铰扭转、偏转性能测试分析及探讨[J].铁道车辆，2011,49(9):9-11.

PENG Li-qun, LIN Da-wen, WANG Jin, et al. Deflection performances of rubber bushing for rolling stock [J]. Journal of Rolling Stock,2011, 49(9):9-11.

[4]Mars W V，Fatemi A. A literature survey on fatigue analysis approaches for rubber [J]. International Journal of Fatigue，2002,24(9):949-961.

[5]Mars W V，Fatemi A. Multiaxial stress effects on fatigue behavior of filled natural rubber [J]. International Journal of Fatigue,2006,28(5-6):521-529.

[7]Kim W D, Lee H J, Kim J Y, et al. Fatigue life estimation of an engine rubber mount [J]. International Journal of Fatigue, 2004, 26(5):553-560.

[8]Li Q, Zhao J C, Zhao B. Fatigue life prediction of a rubber mount based on test of material properties and finite element analysis[J]. Engineering Failure Analysis, 2009,16(7): 2304-2310.

[9]王文涛,上官文斌,段小成,等.基于线性疲劳损伤橡胶悬置疲劳寿命预测研究[J].机械工程学报,2012,48(10):56-65.

WANG Wen-tao, SHANGGUAN Wen-bin, DUAN Xiao- cheng, et al. Study on prediction of fatigue life of rubber mount based on linear cumulative fatigue damage theory[J]. Journal of Mechanical Engineering, 2012, 48(10):56-65.

[10]殷 闻,靳晓雄,仝 光.两种常用橡胶本构模型的有限元分析及仿真[J].上海电机学报,2010,13(4):215-218.

YIN Wen, JIN Xiao-xiong, TONG Guang. Finite element analysis of rubber constitutive models and simulation[J]. Journal of Shanghai Dianji University, 2010,13(4):215-218.

[11]张少实,庄 茁.复合材料与粘弹性力学[M].北京:机械工业出版社,2005:175-176.

[12]Andre N, Cailletaud G, Piques R. Haigh diagram for fatigue crack initiation prediction of natural rubber components[J]. Kautschuk Und Gummi Kunstoffe,1999,52:120-123.

[13]刘建勋,黄友剑,张亚新,等.关于高速列车轴箱拉杆涡杆式橡胶关节承载特性的探讨[J].铁道车辆,2011,49(5):23-26.

LIU Jian-xun, HUANG You-jian, ZHANG Ya-xin, et al. Discussion on mechanical properties of turbo rubber bushing used in axle-box pull rod[J]. Journal of Rolling Stock, 2011,49(5):23-26.

[14]Abraham F, Alshuth T, Jerrams S. The effect of minimum stress and stress amplitude on the fatigue life of non-strain crystallizing elastomers[J]. Mater Des,2005,26(2):39-45.

[15]黄友剑.橡胶材料基础实验及疲劳特性研究报告[R].株洲时代新材料科技股份有限公司,2007.

[16]Luo R K. Cook P W, Wu W X, et al. Fatigue design of rubber springs used in rail vehicle suspensions[J]. Proc. Instn Mech. Engrs. Part F：J. Rail and Rapid Transit,2003, 217(3)：237-240.

[17]Luo R K. Cook P W, Wu W X, et al. An approach to evaluate the service life of rubber springs used in rail vehicle suspensions [J]. Proc. Instn Mech. Engrs. Part F：J. Rail and Rapid Transit, 2004, 218(2):173-177.

[18]Luo R K, Wu W X. Fatigue failure analysis of anti-vibration rubber spring[J].Engineering Failure Analysis,2006, 13(1): 110-116.