蝗虫起跳运动分析及仿生机构研究

倪 虹， 甄永乾， 汪延成， 梅德庆， 陈子辰

(1.浙江大学 流体动力与机电系统国家重点实验室，杭州 310027；2.杭州师范大学 钱江学院 信息与机电工程分院，杭州 310036)

历经生存竞争，自然界生物进化出良好的运动性能，可有效翻越障碍物、躲避天敌袭击。随生物躯体尺寸的减小，原平整的表面亦会变得崎岖不平。因此，小型动物多采用跳跃、飞行等运动方式，以提高越障能力及运动性能[1]。

近年来，已有对青蛙[2]、蝗虫[3-6]、叶蝉[7-8]、跳蛛[9]、跳蚤[10]等小型生物的跳跃运动进行研究。Clark[3]研究表明，一只1.7 g的蝗虫可利用8.65 mJ能量跃过0.95 m水平距离，且起跳速度高达3.2 m/s。而蝗虫起跳阶段能量主要来自跳跃足的肌肉储能[3-4]，其跳跃性能取决于储能量及起跳阶段的运动特性。因此，本文对蝗虫起跳阶段运动特性进行研究，为仿生跳跃机构设计提供依据。

对仿生跳跃机器人已有研究。Scarfogliero等[11]仿生蟋蟀后腿设计的跳跃机器人，采用偏心凸轮驱动四杆机构实现跳跃，并通过添加尾翼及柔性腿提高其起跳、落地的稳定性；Yamakita等[12]模拟猫的蹬墙跳跃运动，提出由两四连杆机构并联构成的跳跃机器人，将其等效为弹簧-质量模型，并对跳跃过程中姿态调节进行了仿真分析；Hvon等[13]研制的仿生狗单足跳跃机器人，将三根连杆作为跳跃腿，两个液压缸作为驱动肌肉，弹簧模拟肌腱，通过压缩弹簧提供推力实现跳跃，用绳索辅助机构提高运动稳定性。Wang等[2]仿生青蛙跳跃，研制出基于四连杆机构的仿生跳跃机器人，跳跃高度相当于其自身高度的3.5倍；陈殿生等[14]根据蝗虫的翻身位姿调节过程，提出跳跃机器人翻身位姿调节机构，实现跳跃机器人翻转功能；李霏等[15]通过仿生叶蝉的跳跃运动，研制出Grillo小型机器人，并加装两翼以提高跳跃的稳定性；Ni等[16]通过研究蝗虫的跳跃机理，提出仿蝗虫跳跃机构，并用运动学仿真分析对其结构进行优化。

本文通过实验对蝗虫起跳阶段运动及力学特性研究结果表明，在起跳阶段蝗虫跳跃足力的输出存在非线性。因此基于仿生蝗虫运动与力学特性，提出仿蝗虫跳跃机构设计方案，进行动力学建模、分析，研制出仿蝗虫跳跃机构原理样机，并进行实验研究。

1 蝗虫跳跃运动实验

1.1 蝗虫跳跃实验研究

据跳跃足在跳跃过程中与地面的接触情况，蝗虫跳跃全周期过程可分为起跳、腾空、着陆三阶段，本文主要针对蝗虫的起跳阶段进行研究。实验用蝗虫为中华稻蝗(Oxya chinensis)，见图1，其身体异律分节成头、胸、腹三个体区，其中胸部为运动中心，有三对胸足、两对翅。胸足分前足、中足、跳跃足，前足及中足主要用于爬行及调节跳跃姿态，跳跃足主要实现跳跃。跳跃足分基节、转节、腿节、胫节、趾节及前趾节六部分。本文所用两只蝗虫的质量及身体各部几何尺寸见表1。

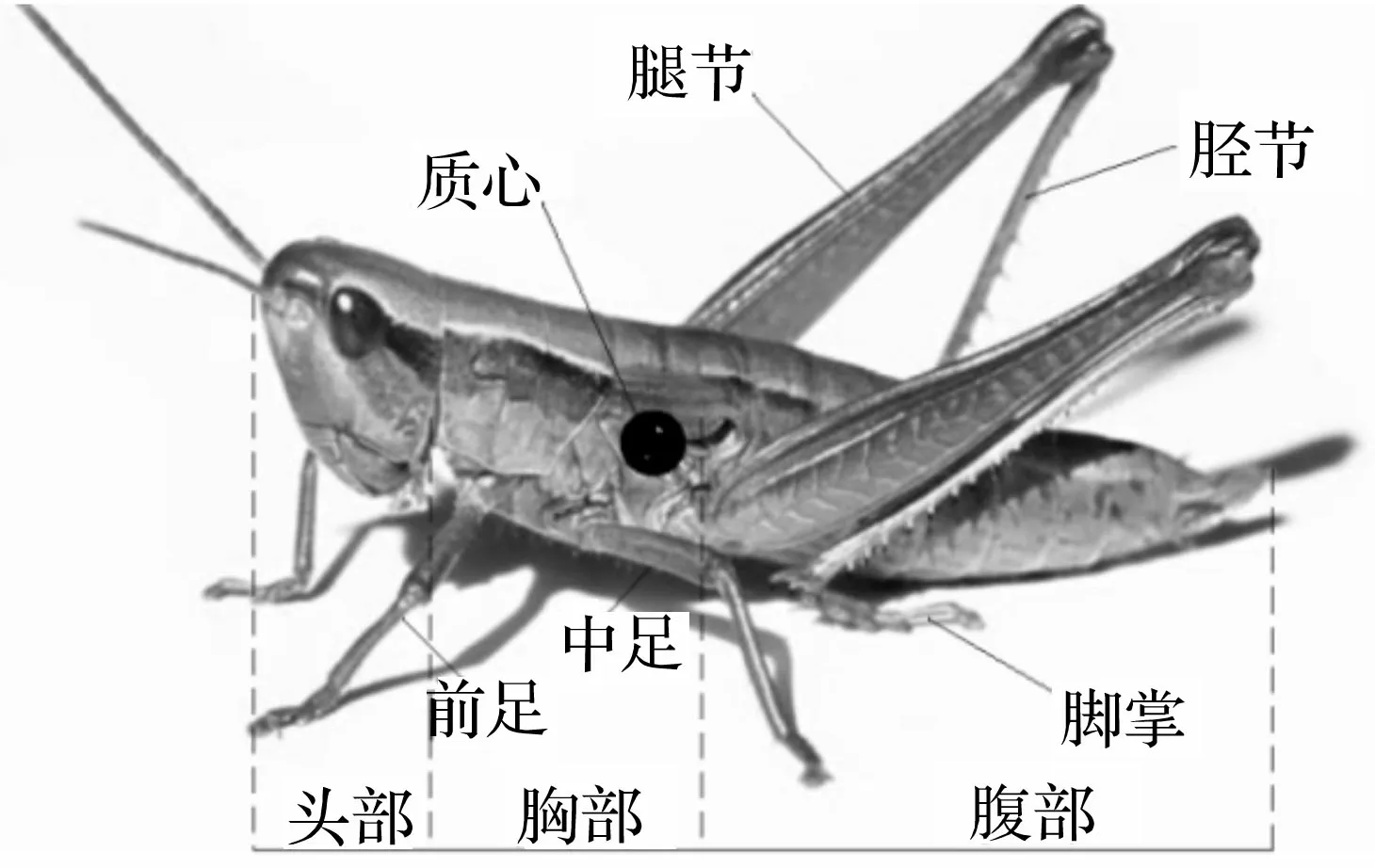
图1 蝗虫身体形态图

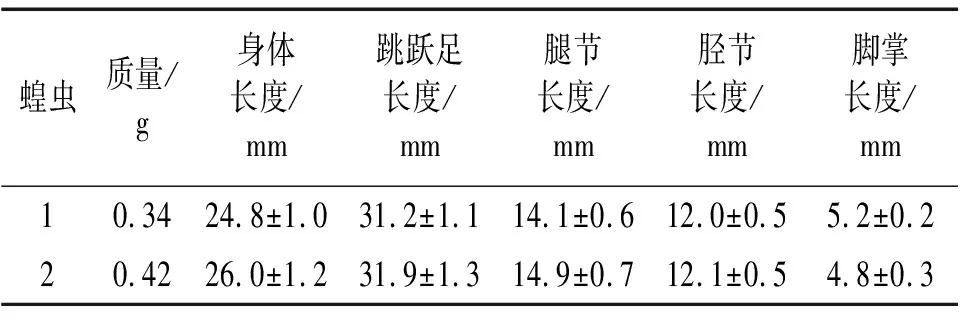
表1 蝗虫质量及几何尺寸测量值

搭建蝗虫跳跃实验测试平台，见图2。包括2个1 200 W恒光源、高速摄像机( MikrotronBLITZ Cube7)、图像采集分析系统及蝗虫。实验中，蝗虫置于实验台上，恒光源对准蝗虫以增强曝光，高速摄像机正向对准蝗虫侧面以1 000 帧/s速度拍摄起跳阶段运动轨迹图像。

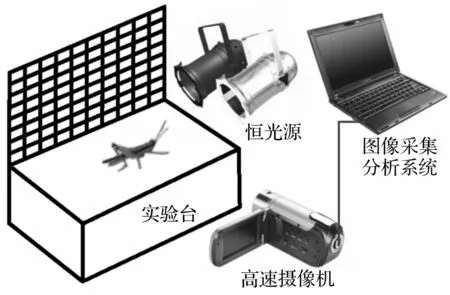
图2 蝗虫跳跃实验测试平台

1.2 蝗虫起跳阶段实验数据分析

蝗虫跳跃运动轨迹主要由起跳角、起跳阶段跳跃足对地面作用力决定，起跳角为胫节与脚掌连接点及基节连线与地面夹角[17]。蝗虫调节起跳角，主要通过前足、中足及跳跃足的协调运动实现，即前足、中足调节身体高度，跳跃足绕基节转动调节起跳角大小。跳跃足对地面的作用力由肌肉收缩引起关节转动产生，该力随时间变化特性决定起跳阶段加速度特性。蝗虫起跳阶段对地面作用力的特性为，脚掌与地面接触面积小，作用时间短，因而难以直接用传感器准确测量。利用高速摄像机捕获蝗虫起跳阶段运动轨迹图像，统计跳跃足起跳过程中关节转角，包括胫节与地面夹角θ1、腿节与胫节夹角θ2、身体与腿节间夹角θ3；通过MATLAB拟合统计的实验数据，获得θ1，θ2，θ3在起跳阶段的变化趋势；通过运动与力学特性分析，获得蝗虫起跳阶段对地面的作用力。

图3(a)、(b)为蝗虫1第一组、第二组运动轨迹图像，图3(c)、(d)为蝗虫2第一组、第二组运动轨迹图像。对比发现，虽蝗虫1与蝗虫2的身体质量、尺寸等存在差异，但起跳阶段的运动特性具相似性。蝗虫的起跳阶段持续约11 ms，前足、中足先离地面，跳跃足各关节继续转动以提高速度直至跳跃足与地面解除约束。起跳阶段，胫节与地面夹角θ1变化范围基本一致，为0°～75°；腿节与胫节夹角θ2变化范围基本一致，约10°～125°，且随θ2的增大，腿节肌肉充分收缩并驱动胫节运动；身体与腿节间夹角θ3在前6 ms时角度基本不变，约145°，随后逐渐增大至180°～220°。不同的蝗虫，θ3在起跳阶段变化范围有所差别，主要由蝗虫起跳角不同引起。在整个起跳阶段，蝗虫身体姿态与初始姿态始终保持一致。

图3 蝗虫起跳阶段各关节转角测量结果曲线

2 蝗虫起跳阶段运动分析

为研究蝗虫起跳阶段运动及力学特性，对蝗虫进行模型简化，见图4。起跳阶段，脚掌粘附于地面[18]，将脚掌与胫节的连接简化为地面支撑点A；腿节与胫节连接处简化为点B；基节长度较短，简化为腿节与身体间连接点C。蝗虫通过跳跃足各关节的协调运动使前足、中足先离开地面，并依靠跳跃足产生的推力实现跳跃。因此，将蝗虫简化为由身体、腿节、胫节三连杆组成的运动机构，杆件之间用平面旋转副连接，蝗虫质心M位于中足与跳跃足之间[19]。设胫节、腿节、基节至质心长度记为l1，l2，l3；在关节A处建立直角坐标系{0}，关节B处建立坐标系{1}，关节C处建立坐标系{2}。

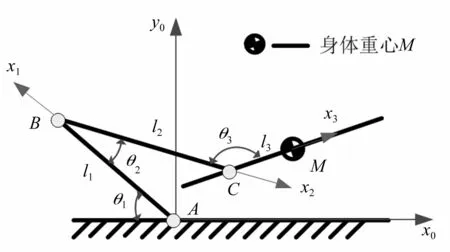
图4 平面连杆机构模型

质心M在坐标系{2}中的位置可表示为：

(1)

利用坐标系间变换矩阵，质心M在坐标系{0}中位置可表示为：

p0=0T11T2P2=

式中：1T2，0T1为坐标系{2}相对于坐标系{1}、坐标系{1}相对于坐标系{0}的变换矩阵。

起跳阶段蝗虫质心M在坐标系{0}中位置为：

(3)

将起跳角记为α，对式(3)求解得质心M位移Lcm、速度vcm、加速度acm及地面对质心的作用力F：

(4)

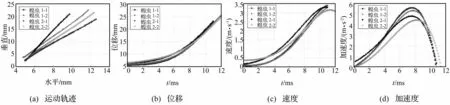
图5 蝗虫质心M运动曲线

将图3中拟合的蝗虫跳跃足各关节夹角数值代入式(3)、式(4)，求解得质心M运动轨迹、位移、速度、加速度及跳跃足对地面作用力，见图5、图6。在起跳阶段，质心M的运动轨迹近似直线(图5(a))，表明蝗虫起跳时起跳角恒定，且分别为65°，69°，76°，68°，跳跃足受地面作用力方向恒定。该特性有利于足部受力相同时能获得最大冲量，从而获得最大起跳速度(图5(b)～图5(d))。在四组跳跃中，蝗虫起跳阶段位移约25 mm，与自身长度相当；且能获得3～3.5 m/s的起跳速度，加速度随时间逐渐增大，达峰值后迅速减小，最大加速度约400～600 m/s2。本文所得蝗虫质心位移、速度、加速度变化规律与文献[3]用直接测量法对沙漠蝗(Schistocerca Gregaria)研究结果基本一致。

起跳阶段，蝗虫受地面作用力变化见图6。开始时受地面作用力较小，随后作用力平缓增大至峰值(0.17～ 0.23 N)，再减小到零，受力峰值出现在起跳过程的后半段，约8 ms处。受地面作用力平缓增大特点，有利于避免地面作用力突变所致肌肉损伤及疲劳破坏。

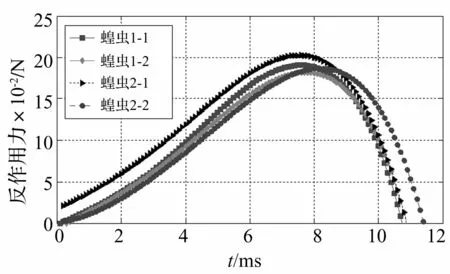
图6 蝗虫起跳阶段跳跃足对地面作用力

3 仿生跳跃机构设计及动力学分析

3.1 仿生跳跃机构设计

由蝗虫起跳阶段运动分析知，蝗虫跳跃运动为腿部多杆件相互协调运动的结果，且质心运动轨迹近似直线，起跳过程中身体姿势始终与起跳初始阶段保持一致。由于跳跃足的胫节与地面、腿节与胫节、身体与腿节之间存在平面内相对转动，因此，可等效为转动副约束；对蝗虫质心线性运动轨迹特性用单自由度滑动副约束实现。本文在仿蝗虫跳跃机构设计中，采用1个滑动副、3个转动副组合进行机构仿生设计，见图7。

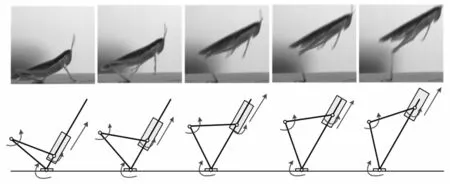
图7 蝗虫与仿生跳跃机构起跳过程对比

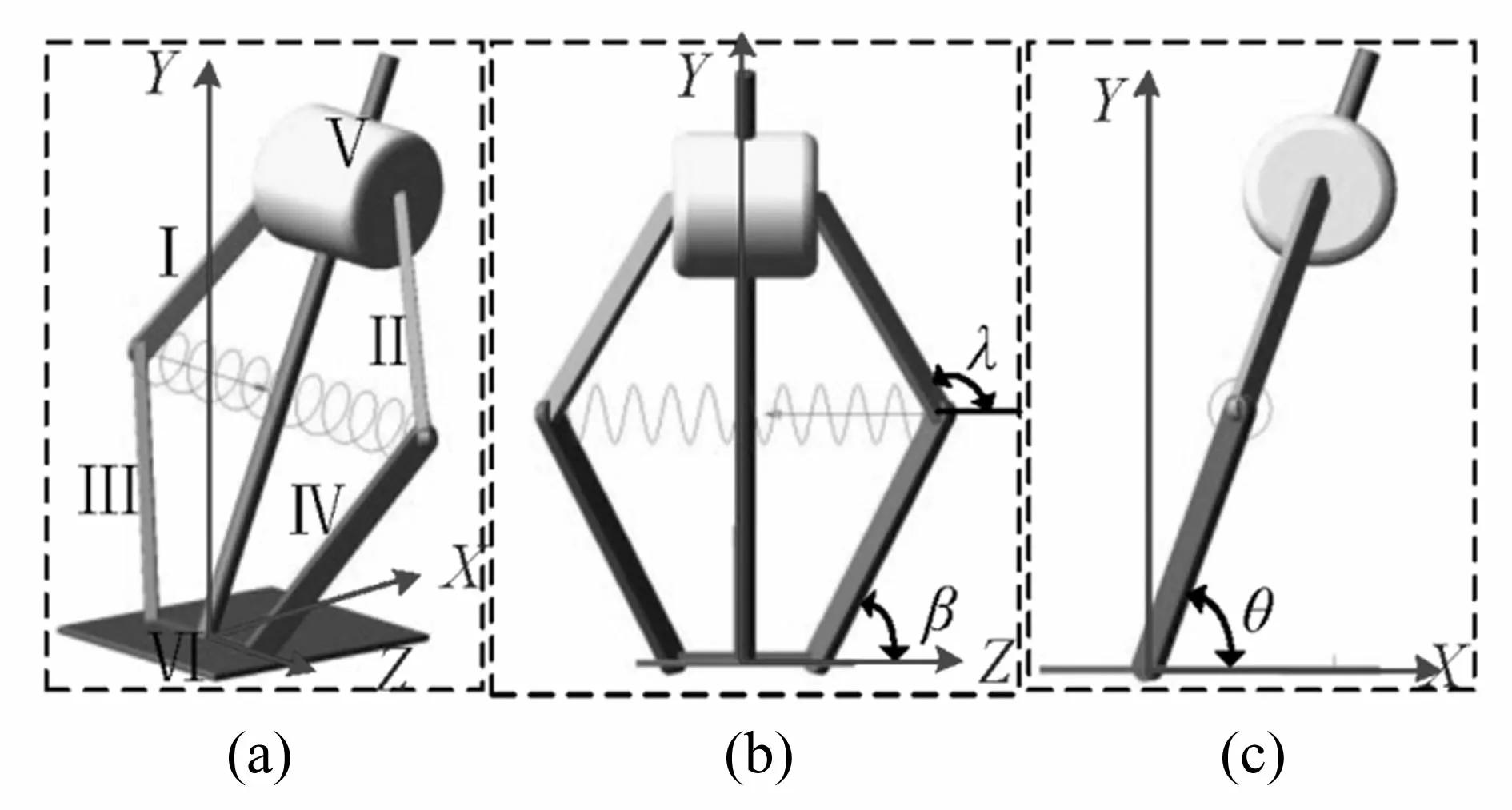
图8 仿生跳跃机构原理图

仿生跳跃机构原理见图8，采用六连杆机构作为腿部构件，其中四连杆(Ⅰ、Ⅱ、Ⅲ、Ⅳ)等长对称布置，用螺旋弹簧储能。为提高储存量，螺旋弹簧两端分别安装在两侧连杆的铰接处，以增大弹簧的拉伸长度。该仿生跳跃机构质量记为m，Ⅰ、Ⅱ、Ⅲ、Ⅳ连杆质量相等，记为m1；跳跃机构起跳角为θ；连杆Ⅳ与Z轴夹角为β；Ⅱ与Z轴夹角为λ。

3.2 仿生跳跃机构动力学分析

为验证设计的仿生跳跃机构在起跳阶段具有与蝗虫相似的运动学特性，对该机构进行动力学分析。令广义坐标为仿生机构弹射方向为r方向，地面为零重力势能面。连杆Ⅲ、Ⅳ绕销轴的转动惯量为J1，J2；绕端点转动动能为K1，K2；连杆Ⅰ、Ⅱ绕质心转动惯量为J3，J4；转动动能为K31，K41；平动动能为K32，K42，则仿生跳跃机构质心M的动能T与势能U分别为：

(5)

式中：a为顶部、底部杆长度；b为两侧连杆长度；l0为弹簧原长；k为弹簧刚度系数；g为重力加速度。

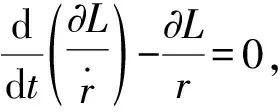
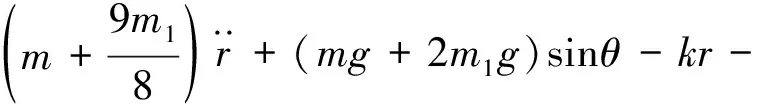
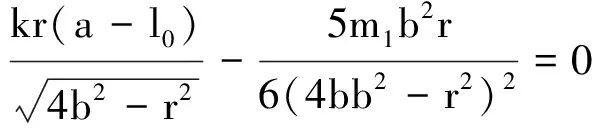
(6)

当机构沿滑动副向下运动至储能结束时，质心距原点距离记为r0，此时速度为零，因此初始条件为：

(7)

据图8仿生跳跃机构，Y轴方向位移y与X轴方向弹簧位移x之关系为：

(8)

由虚功原理Fydy=Fxdx，则有：

(9)

对图8仿生跳跃机构给定参数：身体质量m=0.23 kg；m1= 0.007 kg；弹簧刚度系数k= 1 N/mm；a= 40 mm；b= 60 mm；r(0) = 40 mm；θ= 80°；l0= 70 mm。代入式(6)、式(9)，得仿生跳跃机构质心运动位移、速度、加速度及机构对地面作用力。与蝗虫2-2结果比较见图9。图9(a)～(c)与图9(e)～(g)对比表明，仿蝗虫跳跃机构在起跳阶段运动特性与蝗虫相似，质心加速度曲线为非线性；图9(d)受力曲线显示质心受非线性力作用，表明通过腿部连杆式结构设计及弹簧布置方式，拉伸弹簧产生的线性力能转化为对地面的非线性作用力，能减缓足部与地面间所受瞬时作用力冲击，由此获得在起跳阶段与蝗虫相似的力学特性。

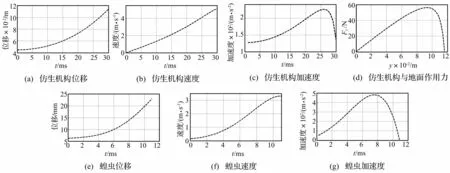
图9 仿生跳跃机构运动特性

4 仿生跳跃机构原理样机研制及实验研究

4.1 仿生跳跃机构原理样机研制

据设计的仿生跳跃机构原型，制作仿生跳跃机构原理样机，见图10，高17 cm，质量0.33 kg。该样机由电机、减速装置、能量存储与释放装置、足部支撑装置等组成。能量存储、释放装置通过ESCAP电机驱动滑块上齿轮箱传动装置，再通过齿轮箱中最后一级缺齿齿轮与固定在导轨两端的齿条啮合(图10(b))，使整个样机上身沿导轨向下运动拉伸弹簧实现能量存储(图10(c))，当缺齿齿轮与齿条脱离啮合时，样机在弹簧力的作用下实现跳跃。

图10 仿生跳跃机构原理样机实物照片

4.2 仿生跳跃机构原理样机跳跃实验研究

为研究样机在起跳阶段的运动特性、力学特性及跳跃性能，用高速摄像机捕获样机起跳阶段的运动轨迹，见图11，起跳阶段持间约44 ms。图11(a)为样机储能后姿态，弹簧拉伸量达最大，由于缺齿齿轮作用，齿轮与齿条即将由啮合状态(图11(b))过渡到非啮合状态(图11(c)～ (f))，并释放出弹簧储存能量。

图12实验结果表明：

(1) 样机能有效仿生蝗虫起跳阶段的运动特性。用高速摄像可获得样机起跳阶段的运动轨迹图像，通过测量样机上身位置随时间变化的具体数值，可得该样机在起跳阶段位移随时间变化曲线(图12(a))。该曲线与图12(d)中蝗虫位移时间曲线及图9(a)中仿生跳跃机构理论分析所得位移时间曲线轨迹近似，表明该样机在起跳阶段能获得与蝗虫相似的位移特性。据样机起跳阶段位移随时间的变化特性，用位移对时间一次微分，可得该样机在起跳阶段速度相对时间的变化曲线(图12(b))，起跳瞬间速度为2.9 m/s，与实验研究中蝗虫在起跳阶段所得起跳速度3～3.5 m/s接近。据样机起跳阶段位移随时间变化特性，用位移对时间二次微分，可得该样机起跳阶段加速度相对时间的变化曲线(图12(c))，最大加速度约86 m/s2，出现于起跳后半段的29 ms时。该加速度特性曲线与图12(f)中蝗虫加速度特性曲线轨迹近似，表明该样机在起跳阶段能获得与蝗虫相似的加速度特性。

(2)样机能有效仿生蝗虫起跳阶段的力学特性。由于该仿生样机质量恒定，地面作用力为加速度与质量的乘积。因此，图12(c)中加速度曲线特性即反映样机起跳阶段对地面作用力曲线特性。在开始阶段，该样机受地面作用力较小，逐渐增大至峰值后迅速减小至零，且受力峰值出现在起跳的后半段。该受地面作用力的变化特性与图6中蝗虫起跳阶段力的变化特性及图9(d)中仿生机构设计理论计算所得力的变化特性一致。

图11 仿生跳跃原理样机起跳阶段运动轨迹图像

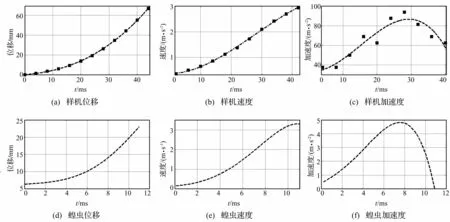
图12 仿生跳跃机构原理样机起跳阶段运动特性

为研究该样机跳跃性能，利用高速摄像机捕获样机跳跃过程运动轨迹图像，见图13。实验结果表明，该样机的跳跃高度可达22 cm，相当于自身高度的129%。图13(a)为该样机在储能完毕后的位姿，起跳角为80°，图13(b)～(g)为样机腾空阶段姿态随时间的变化。由于起跳角固定为80°，故该样机主要实现向上的运动，通过调节起跳角大小可调节跳跃高度及向前位移。

图13 仿生跳跃机构跳跃过程高速摄像图

5 结 论

(1) 对蝗虫起跳阶段运动特性进行研究，利用高速摄像机捕获蝗虫起跳阶段运动轨迹图像，并通过统计分析获得该阶段蝗虫跳跃足各关节的运动曲线。

(2) 对蝗虫起跳阶段进行运动学分析结果显示，其质心运动轨迹可近似为直线，表明蝗虫起跳角恒定，其跳跃足对地面作用力方向恒定，该特性有利于获得最大起跳速度。

(3) 通过对仿蝗虫跳跃机构设计方案的动力学分析表明，该仿生跳跃机构可实现与蝗虫在起跳阶段相似的运动及力学特性。

(4) 通过对仿生跳跃机构原理样机的研制及实验结果表明，该样机在起跳阶段能实现与蝗虫相似的运动特性，跳跃高度为自身高度的129%。

参 考 文 献

[1]Scarfogliero U, Li F, Chen D J, et al. Jumping mini-robot as a model of scale effects on legged locomotion [C]//Proceeding of IEEE International Conference on Robotics and Biomimetics, 2007: 853-858.

[2]Wang M, Zang X Z, Fan J Z, et al. Biological jumping mechanism analysis and modeling for frog robot[J]. Journal of Bionic Engineering, 2008, 5(3):181-188.

[3]Clark H. The energetic of the jump of the locust schistocerca gregaria [J]. Journal of Experimental Biology,1975,63(1):53-83.

[4]Cochrane D, Elder H, Usherwood P. Physiology and ultrastructure of phasic and tonic skeletal musclefibers in the locust,schistocerca gregaria [J]. Journal of Cell Science, 1972, 10: 419-441.

[5]Burrows M, Morris G. The kinematics and neural control of high speed kicking movements in the locust[J]. Journal of Experimental Biology, 2001, 204: 3471-3481.

[6]杨绘宇, 王石刚, 梁庆华,等. 仿蝗虫跳跃机器人起跳过程运动学建模及分析 [J]. 机械设计, 2010, 27(4): 54-57.

YANG Hui-yu, WANG Shi-gang, LIANG Qing-hua, et al. Kinematic modeling and analysis of the take-off procedure of locust-like hopping robot [J]. Journal of Machine Design, 2010, 27(4): 54-57.

[7]Burrows M. Kinematics of jumping in leafhopper insects (hemiptera, auchenorrhyncha, cicadellidae)[J]. Journal of Experimental Biology, 2007, 210(20): 3579-3589.

[8]Burrows M. Anatomy of the hind legs and actions of their muscles during jumping in leafhopper insects[J]. Journal of Experimental Biology, 2007, 210(20): 3590-3600.

[9]Parry D, Brown R. The jumping mechanism of salticid spiders [J]. Journal of Experimental Biology,1959, 36: 654-664.

[10]Clark H. The jump of the flea: a study of energetic and a model of the mechanism [J]. Journal of Experimental Biology, 1967, 47: 59-76.

[11]Scarfogliero U, Stefanini C, Dario P. The use of compliant joints and elastic energy storage in bio-inspired legged robots [J]. Mechanism and Machine Theory, 2009, 44(3): 580-590.

[12]Yamakita M, Omagari Y, Taniguchi Y.Jumping cat robot with kicking a wall[J]. Journal of the Robotics Society of Japan, 1994, 9: 934-942.

[13]Hyon S H, Mita T. Development of a biologically inspired hopping robot-kenken[J].Proceedings of the IEEE International Conference on Robotics and Automation, 2002,4:3984-3991.

[14]陈殿生, 郑万军, 黄 宇,等. 弹跳机器人翻转机构的设计与优化[J]. 机械工程学报, 2011, 47(1): 17-23.

CHEN Dian-sheng, ZHENG Wan-jun,HUANG Yu,et al. The design and optimization of a hopping robot’s tipping mechanism [J]. Journal of Mechanical Engineering, 2011, 47(1): 17-23.

[15]Li F, Liu W T, Fu X, et al. Jumping like an insect: desian and dynamic optimization of a jumping mini robot based on bio-mimetic inspiration[J].Mechatronics, 2012,22(2):167-176.

[16]Ni H, Mei D Q, Zhen Y Q, et al. Design and analysis of bionic jumping leg inspired from locust's jumping mechanism[J]. Advanced Science Letters, 2012, 12(1): 68-72.

[17]Sutton G P, Burrows M. The mechanics of elevation control in locust jumping[J]. Journal of Comparative Physology, 2008, 194(6): 557-563.

[18]Dai Z D, Stanislav G. Contact mechanics of pad of grasshopper (insecta:orthoptera) by finite element methods [J].Chinese Science Bulletin, 2009, 54(4): 549-555.

[19]Chen D S, Yin J M, Zhao K, et al. Bionic mechanism and kinematics analysis of hopping robot inspired by locust jumping[J].Journal of Bionic Engineering,2011,8(4):429-439.