Duffing振子倍周期分岔谱特性

唐元璋， 楼京俊， 翁雪涛, 朱石坚

(1.海军工程大学 动力工程学院，武汉 430033；2.船舶振动噪声重点实验室，武汉 430033)

Feigenbaum[1-4]在所得非线性连续时间动力系统普适理论中对Duffing系统的谱结构进行过详细研究，由第n次倍周期分岔开始，n次所有谱线将成为n+1次倍周期分岔后的偶数项元素，奇数项为新增谱线；n较大时新增谱线平均强度与上次倍周期分岔后新增谱线平均强度相比为常数μ=0.1525，即新增线谱平均强度较上次新增线谱平均强度下降8.18 dB。Wang等[5]亦获得类似递推结论。为验证推导的正确性，Feigenbaum对Rayleigh-Benard湍流系统的倍周期分岔行为分析、实验进行常数验证。Linsay[6]在电路系统中观察到电压幅值倍周期分岔现象，已验证第3、4次倍周期分岔新增线谱平均强度分别接近常数μ。王本仁等[7]进行液氮及水中次谐波实验，观察到次谐波分岔现象。受噪声影响及检测设备限制，第5次分岔新增线谱较难观察，故实验方法验证常数μ的精确性有限。倍周期分岔次数更多时，通常只用数值方法求解方程获得功率谱，此需高频分辨率谱分析才能观察到微弱谱线。Tongue等[8-10]认为数值方法有时因步长选取不当会得到错误结论。以上验证理论结论方法均为数值及实验方法，用近似解析方法求常数μ尚少见。增量谐波平衡法[11-13]为半数值半解析方法，可获得非线性连续时间动力系统高精度高阶谐波解[14]，既能克服实验方法精度难提高缺点，且无需数值方法求频谱过程。本文用增量谐波平衡法以Duffing振子为研究对象，对常数μ进行计算验证理论结论。其中理论推导以非线性连续时间动力系统展开，方法、过程可直接用于其它非线性连续时间动力系统。

1 倍周期分岔线谱变化规律

设N维非线性连续时间动力系统为：

(1)

其中：λn为第n次倍周期分岔参数；T0为激励周期，第n次倍周期分岔后周期Tn=2nT0；x(n)为第n次倍周期分岔后响应，n较大时，周期轨道可近似分成2n个周期为T0的圈，相邻两次倍周期分岔后轨道近似重合。

令：

c(n)(t)=x(n)(t)-x(n)(t+Tn-1)

(2)

式中：上标表示第n次倍周期分岔，第n-1次倍周期分岔后周期Tn-1=Tn/2。据文献[1-4]对分岔间距收敛常数α定义[15]：

(3)

据傅里叶元素定义：

(4)

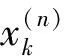
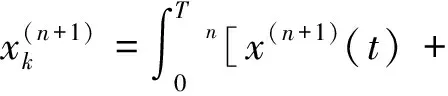
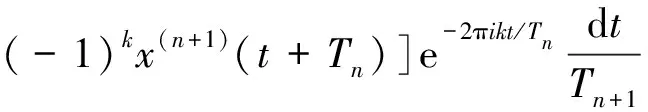
(5)

联合式(3)、(5)推出周期解傅里叶元素奇数项满足：

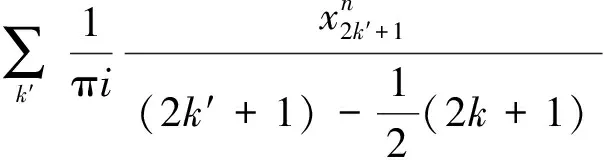
(6)

令2k+1=ξ，2k′+1=ξ′，写成希尔伯特变换式：

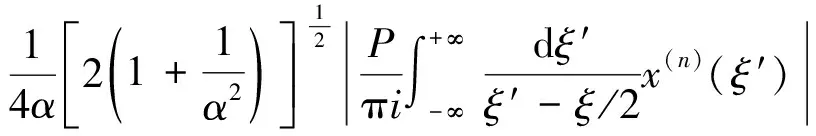
(7)

取P=1，经希尔伯特变换后得：

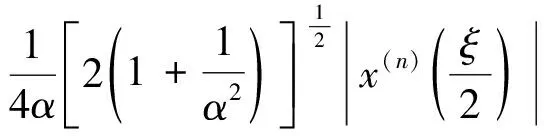
(8)

其中：α=2.502 907 875…为普适分岔间距比，故：

式中：10log10μ=-8.18 dB表示新增线谱平均强度较上次新增线谱平均强度下降8.18 dB。

2 用增量谐波平衡法求Duffing方程周期解

考虑硬弹簧Duffing振子为典型非线性振动模型，其动力学方程经无量纲化后为多项式非线性方程，称Duffing方程：

(9)

为便于计算，式(9)改写为：

(10)

(11)

将式(11)代入式(10)经Taylor展开并略去增量高阶项得：

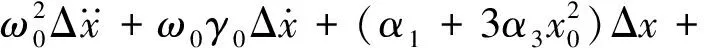
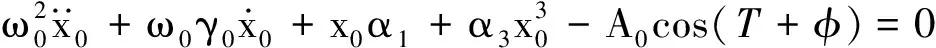
(12)

设周期解初始解x0及增量Δx为：

(13)

(14)

令：

a0=(a0,a1,a2,…,b1,b2,…bNm)

(15)

(16)

Δa0=(Δa0,Δa1,Δa2,…Δb1,Δb2,…ΔbNm)

(17)

则有：

x0=sa0,Δx=sΔa0

(18)

对式(12)应用Galerkin过程：

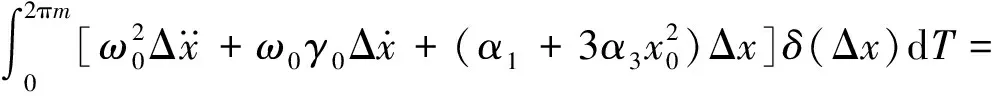
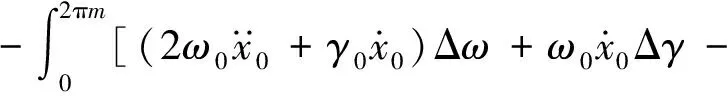
ΔAcos(T+φ)+R]δ(Δx)dT

(19)

其中：

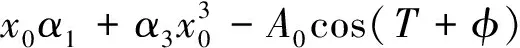
(20)

令：

(21)

(22)

(23)

(24)

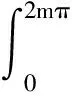
(25)

由式(13)～式(25)得：

KΔa0=PΔω+BΔγ+QΔA+R′

(26)

式(26)为 2Nm+1维线性方程组，选Δω，Δγ，ΔA中之一为增量，x0为初始解，除增量外其余各参数固定；选适当增量步长迭代计算，|R|足够小时可求出Δa0，从而求得周期解x(T)。

3 计算结果

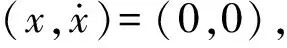
(27)

第k+1次倍周期分岔,周期2k+1轨道预表达式为：

(28)

(29)

(30)

(31)

将式(27)、(28)代替式(13)作为周期解的预表达式，经上节计算过程可求得历次倍周期分岔后分岔点附近的周期轨道x(k)(T)。周期轨道各谱线幅值可按式(29)计算，其中Pi(k)为第k次倍周期分岔后第i条谱线幅值强度；由于相邻两次倍周期分岔后新增谱线均为奇数谱线，相邻两次倍周期分岔后新增谱线平均强度之比μ按式(30)计算；分岔参数收缩率δ按式(31)计算，其中A(k)为第k次倍周期分岔点激励幅值。计算结果见表1。由表1看出，开始两次倍周期分岔因不满足k较大的近似条件，与推导值[1-4]偏差较大，第3、4次倍周期分岔后新增谱线平均强度之比μ4=0.1505已较接近推导值0.1525，且较吻合。

表1 相邻两次倍周期分岔后新增谱线平均强度之比μ及分岔参数收缩率δ

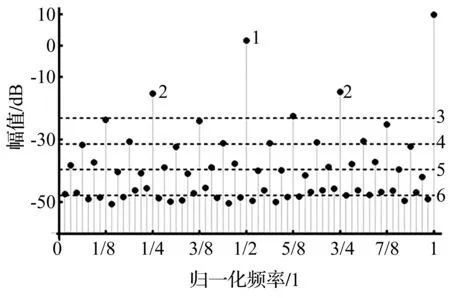
图1 Duffing振子倍周期分岔的谱特性

将1～6次倍周期分岔后分岔点附近周期解归一频率小于1的谱线整合见图1，图中1～6标号与表1中k对应，为1～6次倍周期分岔。第1次倍周期分岔在归一频率1/2处增加的谱线为第1条谱线；第2次倍周期分岔在归一频率1/4、3/4处增加的两条谱线为第1、3条谱线，第1次倍周期分岔后两条谱线仍在原频率位置；第3次倍周期分岔在1/8、3/8、5/8、7/8处增加四条谱线分别为第1、3、5、7条谱线，上次分岔谱线仍在原频率位置。每个倍周期分岔一次，原T倍周期解所有谱线将成为2T倍周期解的偶数项谱线，新增谱线均为奇数项谱线。后续倍周期分岔过程中，偶数项谱线将留在原频率位置。式(29)中Pi(k)为第k次倍周期分岔后第i条谱线幅值强度，图1中横虚线为第k次倍周期分岔后新增谱线幅值平均强度。第k次倍周期分岔后新增谱线幅值平均强度为：

(32)

(33)

(34)

第k+1次倍周期分岔后新增谱线幅值平均强度较第k次约下降8.2 dB。k较大时结果与理论值一致，如第5、6次倍周期分岔后新增谱线幅值平均强度之比μ5取对数运算后结果为10log10μ6=10log100.152 0=-8.18，亦与实验观察结果吻合。μ6=0.152 0见表1。

4 结 论

(1)实验方法只能观察到前4次分岔，本文用增量谐波平衡法能研究前6次分岔。

(2)与数值方法相比，增量谐波平衡法所得近似解析解为谐波组合解，无需考虑频率分辨率，只选傅里叶系数计算相邻两次倍周期分岔新增谱线平均强度之比μ即可，结果与理论结果吻合较好。

(3)本文方法既能验证理论推导的正确性，亦为对数值、实验方法验证理论结论的补充。

参 考 文 献

[1]Feigenbaum M J. Thetransition to aperiodic behavior in turbulent systems[J].Communications in Mathematical Physics, 1980,77(1): 65-86.

[2]Feigenbaum M J.The onset spectrum of turbulence[J]. Physics Letters A, 1979,74(6):375-378.

[3]Feigenbaum M J. Quantitativeuniversality for a class of nonlinear transformations[J]. Journal of Statistical Physics, 1978,19(1):25-52.

[4]Feigenbaum M J. Universal behavior in nonlinear systems[J]. Los Alamos Science,1980,1:2-27.

[5]Wang L Q,Xu M T.Property of period-doubling bifurcations [J]. Chaos,Solitons and Fractals,2005,24(2):527-532.

[6]Linsay P S. Period doubling and chaotic behavior in a driven anharmonic oscillator[J]. Physical Review Letters,1981, 47(19):1349-1352.

[7]王本仁，缪国庆，魏荣爵.在液氮及水中声次谐波的实验观察[J].物理学报,1984,33(3):434-436.

WANG Ben-ren,MIAO Guo-qing,WEI Rong-jue.Experimental observation of subharmonic in liquid nitrogen and water[J]. Journal of Acta Physica Sinica, 1984,33(3):434-436.

[8]Tongue B H. Characteristics of numerical simulations of chaotic systems[J]. ASME，Journal of Applied Mechanics，1987,54(3): 695-699.

[9]Skufca J D. Analysis still matters: a surprising instance of failure of Runge-Kutta-Felberg ODEsolvers[J].SIAM Review, 2004,46(4):729-737.

[10]武际可,周 琨.高维极限环的数值追踪[J].中国科学(A辑)，1994,24(3):269-276.

WU Ji-ke,ZHOU Kun.Numerical tracking of high dimensional limit cycle[J]. Scien in China:Serics A, 1994,24(3):269-276.

[11]Lau S L. The incremental harmonic balance method and its application to nonlinear vibrations[C]. Proceeding of International Conference on Structure Dynamics，Vibration，Noise and Control,Hong Kong,1995:50-57.

[12]Lau S L，Cheung Y K，Wu S Y. Incremental harmonics balance method with multiple time scales for nonlinear aperiodic vibrations[J]. ASME Journal of Applied Mechanics,1983,50: 871-876.

[13]Cheung Y K,Chen S H,Lau S L. Application of the incremental harmonic balance method to cubic nonlinearity systems[J]. Journal of Sound and Vibration,1990,140(2):273-286.

[14]Shen J H,Lin K C,Chen S H, et al. Bifurcation and route-to-chaos analyses for Mathieu-Duffing oscillator by the incremental harmonic balance method[J]. Nonlinear Dynamics,2008,52(4):403-414.

[15]Feigenbaum M J.Presentation functions and scaling function theory for circle maps [J]. Nonlinearity,1988,1(4):577-602.